Simulation of Backflow in Automotive Body Assemblies

Jaedeuk Yun

, Sunghoon Lee

, Jianhui Fu

, Jungwoon Lee

, Yoongho Jung

and Sungbae Park

School of Mechanical Eng., Pusan National Univ., Busan, 609-735, South Korea

Body Manufacturing Eng. Team #3, Hyundai Motor Company, Ulsan, 683-791, South Korea

Keywords: Drainage, Backflow, Octree, Voxel, Gap, CAD.

Abstract: The many parts required for aircraft and automotive development are developed by functional or sectional

design groups for efficiency. Interferences and gaps can be found when the parts and subassemblies from

those design groups are to be assembled. When rainwater enters the spaces between parts and there is not

sufficient drainage, the rainwater within the structure can backflow to gaps or unexpected outlets, which

may cause severe problems of part corrosion and electric shock. We have developed a method and a

program to simulate backflow of rainwater within spaces between automotive parts; the method can find

unexpected outlets and gaps. The developed program can simulate not only simple liquid flows, but also

division and joining of flows with multiple channels. The developed method can also be applied to aircraft

and ship design.

1 INTRODUCTION

Large assemblies such as automobiles, aircraft and

ships have the common characteristic of requiring

huge numbers of parts to be assembled. For such

large assemblies, most developing companies

accelerate the design processes with many design

engineers working concurrently. Concurrent design

with functional or sectional design groups may

reduce development time, but it may cause many

problems of interferences and gaps between parts

that are designed by different designers or design

groups. In particular, gaps between parts can cause

fatal problems of inflow to cabins or other spaces.

Most parts for passenger cars are made of thin

plates to reduce the vehicle weight, and there are

empty spaces between thin parts that are provided to

increase the car body stiffness. If there are gaps

between exterior parts of the car body, rainwater and

water from puddles on roadways can enter the cabin

directly or move through the empty spaces between

body parts. Even though design engineers include

appropriate drainage paths, if the drainage is too

small for fast discharge of the inflow, water may fill

the spaces. This situation may cause corrosion of

interior parts or fatal problems of electric shock and

malfunction if the water enters the electric system.

To check for such problems at the design stage,

designers check gaps between parts in suspect

regions with cross-sectional drawings that are

generated from the assembly model. However, it is

almost impossible for design engineers to check the

gaps of complicated three-dimensional flow paths

with two-dimensional sectional drawings.

To resolve this kind of problem, previous

methods such as searching empty spaces of the

assembly, simulation of fluids (Premoze et al., 2003;

Foster and Metaxas, 1996; Losasso et al., 2004;

Ramaswamy and Kawahara, 1987; Harlow and

Welch, 1965) and mold flow analysis (Broyer et al.,

1975) can be considered. However, those methods

are not adequate for the present purpose, which

requires searching for gaps between parts of

complicated shape and simulating the backflow of

water in the gaps to check whether the backflow

path reaches unwanted places.

We propose a method of searching space

between thin parts of complex shape with free

surfaces automatically to simulate backflow in the

searched space. With the simulation program we

have developed, designers can check the path and

outlet positions of backflows in the design stage, and

can handle the problem of inflow into the cabin by

improving their design before manufacturing.

351

Yun J., Lee S., Fu J., Lee J., Jung Y. and Park S..

Simulation of Backﬂow in Automotive Body Assemblies.

DOI: 10.5220/0003981903510356

In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),

pages 351-356

ISBN: 978-989-8565-20-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 OVERVIEW OF BACKFLOW

SIMULATION

Most car body parts are of thin plate with free

surfaces; the shapes of the gap spaces between those

parts can be complicated. For searching to identify

these spaces automatically, we use a method for

representing the decomposition of the given parts

and spaces that is not limited by the complexity of

the object to be represented and is also efficient for

searching for interior spaces automatically. The best-

known methods for expressing three-dimensional

objects as decomposition models are the voxel and

octree representations (Frieder et al., 1985; Tang,

1992). In this paper, we will modify the combined

method of voxel and octree representation that was

proposed by Rodriguez (2009).

The proposed algorithm starts with input models

having data formatted using STL, which is widely

adopted as a standard CAD model data format. Next,

after representing all parts as octrees of input

resolution, it converts all octants into voxels of the

same size as the minimum octant of the octree. Then

it classifies the interior and exterior spaces of the

input assembly model. Finally, it simulates the

backflow of water within the interior spaces

represented as voxels. A more detailed explanation

is given in the following sections.

3 SEARCHING FOR GAP

SPACES AMONG PARTS

3.1 Generation of Decomposition

Model

The voxel representation method has the advantage

that it is simple to represent a given object and easy

to find neighbor elements. However, small voxels

require more memory and more calculation time is

required to classify each voxel as interior or exterior

to the given assembly. The octree representation

method recursively divides ‘partial’ elements that

contain the boundary of the given object into

elements of the desired resolution. Therefore, the

octree method has the advantages of a smaller

number of elements and less calculation time than

the voxel method. On the other hand, the voxel

representation method can simulate flows more

realistically with uniform elements than the octree

method. In this paper, we combine the voxel and

octree methods to exploit the advantages of both

methods.

For understanding of the combined method, we

will explain using the two-dimensional illustration

shown in Figure 1. First, we represent each part as

an octree (quadtree in Figure 1(a)) of which the root

octant is a cube (the main box in Figure 1(a))

containing the main assembly, instead of making the

root octant the part itself, as shown in Figure 1(a).

Then, we divide the cube (the box in Figure 1(b))

containing all ‘partial’ octants of the octree into

voxels of the same size as the minimum octant of the

octree, as shown in Figure 1(b). This approach has

the following advantages. First, it is much faster

than the original voxel representation method.

Second, it is easier and faster to find neighbor

elements than in the original octree representation.

(a) Octree generation

(b) Voxel generation

Figure 1: Voxel generation from octree representation.

To generate the decomposition model of the

assembly, we combine the voxel models of each part

using Boolean operations, as shown in Figure 2,

which shows the process of generating the

decomposition assembly model of two parts in two

dimensions. When the voxel models for Part 1 and

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

352

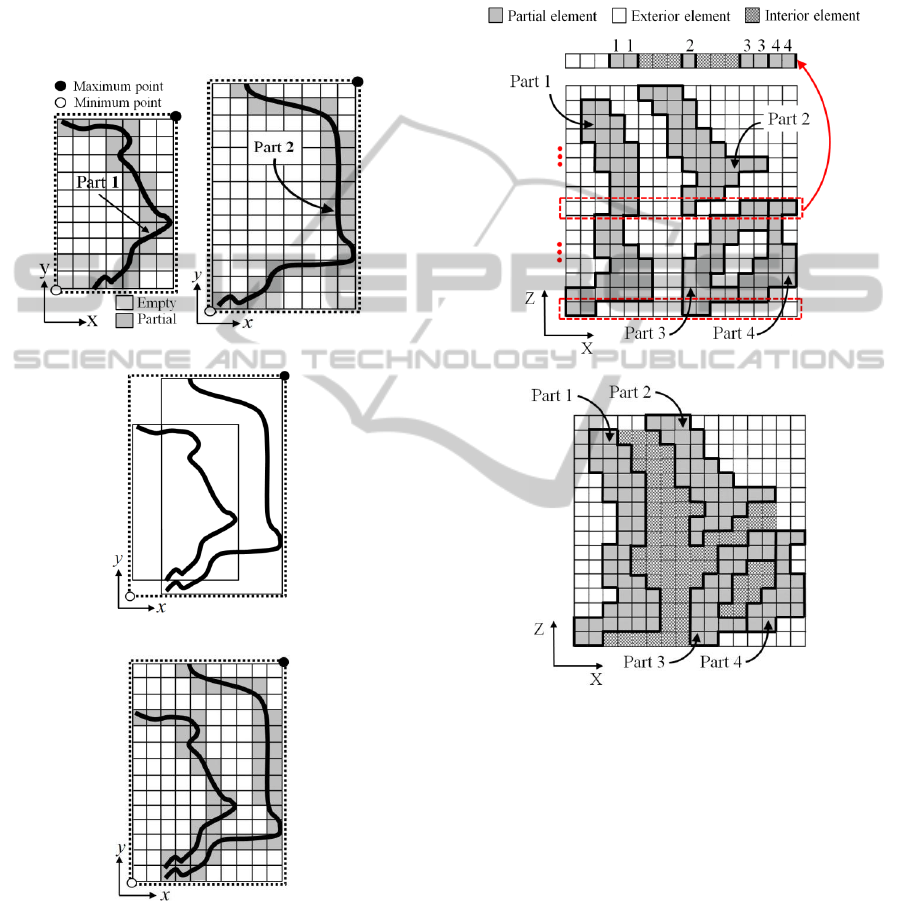
Part 2 are generated, as shown in Figure 2(a), we

calculate the minimum cube (the box in Figure 2) as

in Figure 2(b) to contain both voxel models. After

dividing the minimum cube into voxels of the same

size as the voxels of the parts, we map each voxel of

Part 1 and Part 2 onto the corresponding voxel of the

minimum cube, as shown in Figure 2(c). This

process continues for all parts to generate the

decomposition model of the whole assembly.

(a) Voxel model of each part

(b) Mapping

Figure 2: Boolean operation for assembly model.

3.2 Searching for Interior Elements

When parts of free surfaces are assembled, it is

difficult to define the boundaries between gap spaces

between parts and exterior spaces of the assembly.

In this paper, we propose an algorithm to define the

boundary when each part is represented by a

decomposition model of voxels. To understand the

proposed algorithm, we will explain using two

dimensions as shown in Figure 3, in which the

model consists of four parts.

(a) Interior elements in X-axis direction

(b) Result of searching interior elements

Figure 3: Interior elements among parts.

With the decomposition assembly model of all

parts, the proposed method searches for every voxel

within the gap spaces as follows. Our method visits

each voxel of the decomposition assembly model in

the X-, Y-, and Z-axis directions, searching for

voxels that are between ‘partial’ voxels that belong

to different parts, to be classified as ‘interior

element’ (IE) voxels. For example, in Figure 3(a),

visiting voxels from left to right (the X-axis

direction) in the eighth row from the bottom, we

classify the voxels in the sixth, seventh, and eighth

columns as IEs, because they lie between partial

elements of Part 1 and Part 2. The voxels in the 10th,

11th, and 12th columns are also IEs because they lie

between partial elements of Part 2 and Part 3. We

Simulation of Backflow in Automotive Body Assemblies

353

continue the process from the bottom to the top row

to search for all interior elements in the X-axis

direction. In the same way, after searching in the Y-

axis direction, we can find all interior elements, as

shown in Figure 3(b). For the three-dimensional

case, we also search in the Z-axis direction.

4 BACKFLOW SIMULATION

ALGORITHM

In this section, we will describe the simulation

algorithm for backflow when fluid fills the interior

spaces between car body parts. For the purpose of

the algorithm, we will call a voxel that is being filled

with fluid ‘half occupied’ (HO), and a voxel that has

been completely filled ‘completely occupied’ (CO).

4.1 Backflow Simulation in the Vertical

Direction

First, the algorithm searches the voxel model for the

IEs that are on the lowest level or have an exterior

element (EE) below, to form a current layer (CL)

with all neighboring IEs. We will describe the

algorithm for forming the CL in the next subsection.

Next, when there is any IE below the CL during

the simulation process, the status of all elements of

the CL is set to HO, and the layer below the CL is

made a new CL with all neighboring IEs on the

same level. However, when there is no IE below the

CL while there is any IE or HO element above the

CL, the status of all elements of the CL is set to CO,

and the layer above the CL is made the new CL with

all neighboring IEs and HO elements on the same

level. All CO elements are regarded as filled with

fluid. This process continues until there are no IE or

HO elements above the CL. This approach allows us

to simulate forks into several streams as well as

joining of flows.

For understanding of the proposed backflow

algorithm, we will explain with the two-dimensional

illustration in Figure 4. The algorithm has five parts.

First, the algorithm searches from the lowest layer

for IEs that are above EEs, such as voxels ‘A’, ‘B’

and ‘C’ in Figure 4(a). When the user selects one of

these voxels, for example ‘A’ or ‘B’, the algorithm

forms a CL including the selected voxel. Because

there is no IE below the CL, the algorithm searches

for an IE above the CL and makes the layer

including the IE a new CL, while it changes the

status of all voxels of the previous CL to CO. This

process continues until the seventh layer from the

bottom in the case shown in Figure 4(a). At the

eighth layer, there are IEs below the CL, so the

algorithm searches downward layer by layer until it

reaches the bottom, as shown in Figure 4(b). Then,

because the CL at the bottom does not have any IEs

below, the process continues upward again, as

shown in Figure 4(c). When forming the CL,

separate HO elements at the same level as the CL

are included as CL elements. The algorithm

continues until there are no IE or HO elements

above the CL, as shown in Figure 4(d). The

proposed algorithm can simulate not only filling

enclosed spaces between parts, but can find

positions of outlet that can be passages of fluid into

the cabin. If the user selects voxel ‘C’ as the starting

CL, the algorithm will simulate a separate filling

process for the separate gap space.

4.2 Backflow Simulation in the

Horizontal Direction

We now describe the process of searching for all

elements of the CL that are on the same level and are

to be filled with fluid. When an IE in a layer is

(a) (b) (c) (d)

Figure 4: Algorithm for backflow simulation in the vertical direction.

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

354

identified as a current IE, the algorithm searches for

neighbor IEs that are left, forward, right, and

backward from the current IE. When it finds a

neighbor IE, it makes that neighbor the current voxel

and changes the status of both elements to HO. The

process continues until the current voxel has no

unsearched neighbor IEs. The algorithm continues to

return to a previous voxel recursively while there is

an unsearched neighbor IE, to search again for

neighbor IEs. The solid arrows in Figure 5 show the

search direction while the dotted arrows represent

the returning process when the current voxel has no

unsearched neighbor IEs. The proposed algorithm

can find all voxels that are within an enclosed

boundary on the same level.

Figure 5: Algorithm for filling simulation in the horizontal

direction.

5 APPLICATION EXAMPLE

We have implemented the proposed algorithm using

Microsoft Visual Studio 2008 and applied it to

assemblies of real automotive parts. Figure 6(a)

shows the input STL models of an outer panel, front

pillar, and inner pillar, while Figure 6(b) represents

the result of searching for interior spaces between

the parts as voxels. Figure 6(c) shows the results of

the backflow simulation, which automatically found

several outlets for water from an inlet that was not

fully discharged at the designed outlet and thus filled

up the interior space between the parts. Our program

can simulate backflow dynamically and identify

outlet locations such as backflow outlets 1 and 2 in

Figure 6(b) that might be the result of design errors.

(a) Parts of STL file (b) Interior elements

Figure 6: Application example of backflow simulation.

6 CONCLUDING REMARKS

In this paper, we have suggested a method for

finding the spaces between automotive body parts

and searching for backflow paths to be visualized in

a decomposition model. The developed program

based on our method has the following advantages.

First, the developed program can simulate upward

and downward backflow in the enclosed spaces and

can also simulate forks into several streams as well

as join flows graphically. In addition, it can find the

positions of inflows to the vehicle cabin when there

are unexpected flow paths and gaps caused by

design errors. Therefore, with the developed

program, designers can find these design errors

before the manufacturing stage, which can reduce

the development period and cost. Second, the

proposed method is not limited by the complexity of

the given assembly because it represents the

assembly and gap spaces as a decomposition model.

Our method with combined octree and voxel

representation has the advantages of both methods

Simulation of Backflow in Automotive Body Assemblies

355

without increases in calculation time compared with

the octree or voxel methods alone. Finally, as well as

for developing automotive designs, it can be used for

aircraft and ships for which many plate-shaped parts

must be assembled.

ACKNOWLEDGEMENTS

This work was partially supported by NCRC

(National Core Research Centre) program through

the National Research Foundation of Korea funded

by the Ministry of Education, Science and

Technology (2011-000-6253) and by a grant from

the International Collaborative R&D Program

(0420-2011-0161) of Korea Institute of Energy

Technology Evaluation and Planning (KETEP),

funded by the Korean government’s Ministry of

Knowledge Economy.

REFERENCES

Broyer, E., Gutfinger, C. and Tadmor, Z. (1975). A

theoretical model for the cavity filling process in

injection molding. Transactions of the Society of

Rheology, 19(3), 423-444

Foster, N. and Metaxas, D. (1996). Realistic animation of

liquids. Graphics Models and Image Processing, 58(5),

471-483.

Frieder, G., Gordon D. and Reynolds, R. A. (1985). Back

to-front display of voxel based objects. IEEE

Computer Graphics and Applications, 5(1), 52-60.

Harlow, F. H. and Welch, J. E. (1965). Numerical

calculation of time-dependent viscous incompressible

flow of fluid with free surface. The Physics of Fluids,

8(12), 2182-2189.

Losasso, F., Gibou, F. and Fedkiw, R. (2004). Simulating

water and smoke with an octree data structure. ACM

Transactions on Graphics, 23(3), 457-462.

Premoze, S., Tasdizen, T., Bigler, J., Lefohn, A. and

Whitaker, R., T. (2003). Particle-based simulation of

fluids. Eurographics, 22(3), 401-410.

Ramaswamy, B. and Kawahara, M. (1987). Lagrangian

finite element analysis applied to viscous free surface

fluid flow. International Journal for Numerical

Methods in Fluids, 7, 953-984.

Rodriguez, A. (2009). Automatic extraction of the

topology of 3D electrical mock-ups using a mixed

octree-voxel method. Advances in Engineering

Software, 40, 570-582.

Tang, Z. (1992). Octree representation and its applications

in CAD. Journal of Computer Science and Technology,

7(1), 29-38.

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

356