Using Linear Systems Theory to Study Nonlinear Dynamics of

Relay Cells

Rahul Agarwal and Sridevi V. Sarma

Institute for Computational Medicine, Johns Hopkins University, 3400 N Chrles Street, Baltimore, U.S.A.

Keywords:

Relay Neurons, Thalamus, Reliability, Hodgkin Huxley Type Models.

Abstract:

Relay cells are prevalent throughout sensory systems and receive two types of inputs: driving and modulating.

The driving input contains receptive ﬁeld properties that must be relayed while the modulating input alters

the reliability of this relay. In this paper, we analyze a biophysical based nonlinear model of a relay cell

and use systems theoretic tools to construct analytic bounds on how well the cell transmits a driving input

as a function of the neuron’s electrophysiological properties, the modulating input, and the driving signal

parameters. Our analysis applies to both 2

& 3

order model as long as the neuron does not spike without

a driving input pulse and exhibits a refractory period. Our bounds suggest, for instance, that if the frequency

of the modulating input increases and the DC offset decreases, then reliability increases. Our analysis also

shows how the biophysical properties of the neuron (e.g. ion channel dynamics) deﬁne the oscillatory patterns

needed in the modulating input for appropriately timed relay of sensory information.

1 INTRODUCTION

Relay neurons are found in various brain nuclei in-

cluding the thalamus (Samuel et al., 2004; Hirsch

et al., 1983; Seki et al., 2003). Experiments have

suggested that the inputs to a relay neuron can be

divided into two categories: driving and modulat-

ing. The driving input is made up of few synapses

on the proximal dendrites whereas the modulating in-

put comprises all other synapses (Guillery and Sher-

man, 2002) (see Figure 1). The relay neuron pro-

cesses and relays information in the driving input,

conditioned on the modulating input.(Sherman and

Guillery, 1998; Sherman, 2007). For example, the

lateral geniculate nucleus (LGN) in the thalamus re-

ceives the driving input from the retina and modu-

lating input from cortex. The function of the LGN

is to selectively relay information from the retina to

primary visual cortex (Guillery and Sherman, 2002;

O’Connor et al., 2002).

In this study we rigorously analyze biophysical

based models of relay neurons and characterize the

nonlinear electro-physiological dynamics of a single

relay cell as a function of the cell type and the inputs.

Various attempts to study relay neurons are made in

(Rubin and Terman D., 2004; Masson et al., 2002;

Guo et al., 2008; Wolfart et al., 2005; Rubin and Josic

K, 2007). These studies also suggest that the relay

neuron’s reliability is governed by the modulating in-

put combined with the intrinsic properties of the neu-

ron, however the results were shown to be true for

only few realizations of modulating and driving input.

The work presented here is an extension of the work

we presented in (Agarwal and Sarma, 2011) where

we employ systems theoretic tools to obtain an ex-

plicit analytical bounds on reliability for a 2

order

model. In this work we showed that same method-

ology can also be employed to obtain bounds on 3

order model as long as the neuron does not spike with-

out a pulse in the driving input and exhibits a refrac-

tory period. Consequently, our analysis is relevant for

relay cells whose electrophysiological dynamics, in-

cluding bursting, may be governed by several differ-

ent ion channels and is more rigorous than previous

works. Our bounds predict the dependence of relay

reliability as a function of the neuron’s electrophysio-

logical properties (i.e., model parameters), the modu-

lating input signal, and the driving signal parameters.

Our lower and upper bounds suggests, for example,

that if the frequency of the modulating input increases

and/or its DC offset decreases, then relay reliability

increases.

433

Agarwal R. and V. Sarma S..

Using Linear Systems Theory to Study Nonlinear Dynamics of Relay Cells.

DOI: 10.5220/0003987504330438

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 433-438

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 MATERIALS AND METHODS

In this section, ﬁrst we describe a biophysical model

of a relay neuron, and then use systems theoretical

tools to compute bounds on relay reliability.

2.1 A Relay Neuron Model

A relay neuron receives two kinds of inputs: a driving

input, r(t) and a modulating input u(t), and generates

one output, V (t), as shown in Figure 1.

Below is a state space representation of 3

order

Hodgkin-Huxley type biophysical model of a relay

neuron. This model was used in (Guo et al., 2008;

Rubin and Terman D., 2004), which is a simpliﬁca-

tion of model used in (Sohal and Huguenard, 2002;

Sohal et al., 2000). The response of the model for

an oscillating modulating input and a Poisson driver

input is also shown in Figure 1.

x = f(x) +





−u(t) 0 0

0 0 0





x +





r(t)





, (1)

where f(x) =







−(I

+ I

) + I

ext

∞

syn

)−X

)

(τ

syn

))

∞

syn

)−X

)

(τ

syn

))







. (2)

Here I

= g

(V − V

) , I

= g

∞

h(V − V

= g

(0.75(1 − h))

(V − V

) are the leak current,

sodium and potassium current respectively. I

∞

(V )r(V − V

) and I

ext

are the low threshold

potassium current and external current respectively.

All the parameters used are same as those in (Guo

et al., 2008) and are given in the table 1.

In general, a state space representation takes the

form

x = f(x,r,u), however, there is more structure

in (1). From (1), one can see that f(x) is only a func-

tion of the system’s internal states. The modulating

input, u(t), multiplies the ﬁrst component of the state

x, while the driving input, r(t), is an exogenous input

to the system.

2.1.1 Inputs and Outputs

For our analysis, we assume that the driving input

belongs to class of delta pulse train with Poisson ar-

rivals, i.e. r(t) = I

∑

i=1

δ(t − τ

). The τ

s are generated

randomly such that τ

i+1

= τ

+ T

+ τ

, where T

∈ R

is a constant that represents the refractory period of

driving input, and τ

∈ R

is exponentially distributed

Figure 1: A Relay Neuron - Illustrating a relay neuron.

Ensemble activity of all the distal synapses (stars) is modu-

lating input u(t). The proximal synapses (diamonds) form

driving input r(t). The output is axonal voltage V (t). The

inset plots the voltage proﬁle obtain from the model in re-

sponse to pulses in r(t). Note that each pulse in r(t) may or

may not generate a spike.

with rate λ. Therefore, the average inter-pulse interval

is T = E(τ

i+1

− τ

) = T

+ 1/λ. We assume that the

modulating input belongs to set of sinusoidal func-

tion i.e. u(t) = c

sin(ωt). The output of the relay

neuron is membrane voltage V (t) = x

(t) +V

syn

. De-

tails of all the parameters and reasons for the chosen

classes for driving and modulating input can be found

in (Agarwal and Sarma, 2011).

2.1.2 Properties of the Model

Finally, the function f(x) is assumed to have the fol-

lowing properties but is otherwise general:

1. Stable Neuron. Consider (1) with u(t) = c

and

r(t) = 0,. In general, this system may have multiple

equilibria with different stability properties. But for

our purposes, we choose f(x) such that (1) with u(t) =

,r(t) = 0 has only one globally stable equilibrium

point,

x, for all pragmatic c

. Such a neuron is called

a stable neuron (Manor et al., 1997). This condition

ensures that the neuron does not have any limit cycle,

therefore, the neuron does not spike without a pulse

in r(t).

This further implies that if a small periodic mod-

ulating input is applied to a stable neuron (1), u(t) =

sin(ωt),r(t) = 0, then after a sufﬁcient amount

of time the system’s state vector will lie within a small

neighbourhood of the equilibrium point. However,

the state vector never reaches

x due to the time vary-

ing modulating input. The trajectory of the state in

this neighbourhood can be solved using linearization

methods and is periodic (Agarwal and Sarma, 2011).

We deﬁne this periodic trajectory as the steady state

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

434

orbit of a stable neuron, x

(t). See Figure 2 A.

Next, we deﬁne X

∞

as the collection of all points

in the steady state orbit. If the initial state of the sys-

tem x(t = 0) /∈ X

∞

then X

∞

is not achievable in ﬁnite

time. Therefore, we relax our deﬁnition to the collec-

tion of all points inside a tube of ε thickness around

the steady state orbit, and deﬁne this tube as the set

, i.e.

= {x ∈ R

| kx −vk ≤ ε for a v ∈ X

∞

}. (3)

2. Threshold Behaviour. To deﬁne threshold be-

haviour of a neuron, we ﬁrst deﬁne a successful re-

sponse. A successful response at time t is a change

in V such that V (t) > −50mV & V (t − τ) ≤ −50mV

∀τ ∈ (0, L)ms. Note that both a single spike or a burst

of spikes, with intra burst interval less than L ms, are

counted as a successful response under this deﬁnition.

We use this deﬁnition so that we can extend our anal-

ysis to bursty neurons characterized by higher order

models.

Almost all stable neurons show a threshold be-

haviour (Platkiewicz and Brette R, 2010; Lodish

et al., 2000).

Now, we deﬁne x

= V

−V

syn

, where V

is the

traditional threshold voltage for generating a success-

ful response (Platkiewicz and Brette R, 2010; Lodish

et al., 2000; FitzHugh, 1955). In (Platkiewicz and

Brette R, 2010) it has been shown that spike threshold

is inﬂuenced by ion channels activation and synap-

tic conductance. In our case we assume a constant

threshold for simplicity. We show in results section

that our analytical bounds calculated using this as-

sumption contained the relay performance obtained

by doing simulations on the original model. Fi-

nally, we deﬁne the threshold current, I

, such that

¯x

= x

. Note, by deﬁnition both I

and V

have

the same units and hence can be added.

Illustrations of a successful response, unsuccess-

ful response, I

, V

, x

∞

, X

are shown in Figure

2 A B, C, for a second order system. Note that, I

and V

are functions of c

, since different values of

result in different F(x). This dependence is a lin-

ear function i.e I

) ' I

(0) + mc

2.2 Response to Pulses in r(t)

When a reference pulse arrives, there are 2 possible

responses of system in (1). The neuron either gives

a successful response or unsuccessful response. In

Figure 2 C, we have plotted these two types of re-

sponses.

It is straightforward to see how these two re-

sponses occur. The reference pulse causes the state

vector to “ jump” to x(t

) = x(t

−

) + [I

,0]

. This is

easy to show by direct integration of (1), on the time

interval lim

∆t→0

− ∆t,t

]. If the dynamics of x

are slow and x

) > x

− I

(see Figure 2 A,B) the

neuron will generate a successful response, otherwise

it will return back to the equilibrium point generat-

ing unsuccessful response. Now, we deﬁne set X

as the collection of points in X

whose ﬁrst compo-

nent x

> x

− I

. These points result in successful

response after a pulse in r(t). Similarly we deﬁne

⊆ X

as the collection of points whose ﬁrst com-

ponent x

≤ x

− I

, hence these points result in un-

successful spikes after a pulse in r(t). These sets are

illustrated in Figure 2 A. Note that if the reference

pulse does not occur for a T

time interval i.e, the sys-

tem state will move into X

Figure 2: Properties of f(x) - (A) Illustrates the equilib-

rium point

x, the steady state orbit x

(t) and the orbit tube,

, for f(x) for a second order neuron. (B) Illustrates x

the threshold voltage V

and threshold current I

. Note

that these parameters are deﬁned by the undriven system

u(t) = c

,r(t) = 0. (C)Illustrates a successful response tra-

jectory and an unsuccessful response trajectory.

2.3 Relay Reliability

We deﬁne relay reliability as:

R , Pr(Successful spike due to a reference pulse ).

(4)

Using (4) and deﬁnition of X

, we can write:

R = Pr



X(t

−

) ∈ X

|r(t) = I

δ(0)



(5a)

= Pr (X(t

) ∈ X

) for any i = 1,2,··· . (5b)

UsingLinearSystemsTheorytoStudyNonlinearDynamicsofRelayCells

435

Noting X

⊆ X

, we break (5b) as:

R = Pr (X(t

) ∈ X

) (6a)

= Pr (X(t

) ∈ X

)Pr (X (t

) ∈ X

|X(t

) ∈ X

) (6b)

, P

pulse

× P

spike

. (6c)

Here we have used the deﬁnition of conditional

probability (Greenstied and Snell, 2003) to go from

(6b) to (6c). Although not explicit in (6), relay re-

liability is a function of the driver input parameters,

and T, the modulating input parameters, c

, and

ω, and the neuron’s dynamics (i.e. model parame-

ters) denoted by H. In the next section, we com-

pute closed-form approximations of lower and upper

bounds of reliability as a function of I

,T, c

,ω and

H, by computing P

spike

and bounds on P

pulse

2.4 Calculation of P

spike

We have already calculated P

spike

for a second or-

der model and is same as R in (Agarwal and Sarma,

2011). The exact analysis can be repeated for the 3

order models and P

spike

can be estimated as the ra-

tio of time spent by the state trajectory in X

and X

given it is in X

. This gives:

spike

π + 2sin

−1



−I

( jω)| ¯x



2π

. (7)

Here H

( jω) =

2π

(t)e

− jωt

dt is the transfer

function of the neuron x

(t) − ¯x

= h

∗ u(t). Details

of the above expression can be found in (Agarwal and

Sarma, 2011).

2.5 Calculation of P

pulse

& R

In this section, we compute P

pulse

to ultimately obtain

an expression for R. Since a driver pulse that arrives

at time t

can only result in either a successful spike or

an unsuccessful spike, we can equivalently write the

deﬁnition of P

pulse

as:

pulse

=Pr(x(t

) ∈ X

| SR at t

i−1

) · Pr(SR at t

i−1

)

+ Pr(x(t

) ∈ X

| USR at t

i−1

) · Pr( USR t

i−1

(8a)

Here, we have used the law of total probability and

the deﬁnition of conditional probability (Greenstied

and Snell, 2003) to arrive at (8a). We know that after

a successful spike at t

i−1

, the system state X (t) /∈ X

only for t ∈ (t

i−1

+ T

). Therefore, we see that

Pr(X (t

) ∈ X

| SR at t

i−1

) = Pr(t

−t

i−1

≥ T

). (9)

Similarly, if T

denotes time to resting tube after un-

successful spike, then we get:

Pr(X (t

) ∈ X

| USR at t

i−1

) = Pr(t

−t

i−1

≥ T

(10)

As T

has complex dependence upon input and

model parameters it is hard to calculate Pr(t

−t

i−1

≥

). However, it is certain that T

≤ T

. This implies

that Pr(t

−t

i−1

≥ T

) ≤ Pr(t

−t

i−1

≥ T

), by prop-

erties of cumulative distributive functions (Greenstied

and Snell, 2003). Therefore, we get the following

bounds:

Pr(t

−t

i−1

≥ T

) ≤ Pr(t

−t

i−1

≥ T

) ≤ 1 (11)

Putting together (8a),(9),(10) and (11), we get:

pulse

≥R · Pr(t

−t

i−1

≥ T

) (12a)

+(1 − R) · Pr(t

−t

i−1

≥ T

) (12b)

and P

pulse

≤R · Pr(t

−t

i−1

≥ T

) + (1 − R). (12c)

Now we calculate Pr(t

− t

i−1

≥ T

). Recall that

the inter pulse intervals of r(t), t

−t

i−1

= τ + T

, here

τ is generated from an exponential distribution and T

is refractory period. Therefore:

Pr(t

−t

i−1

≥ T

) = Pr(T

+ τ ≥ T

) (13a)

= Pr(τ ≥ T

− T

) (13b)

∞

−T

(τ)dτ , α. (13c)

It can be easily shown that:

α =

(

−(T

−T

)

T −T

− T

≥ 0

1 T

− T

< 0

. (14)

Here T is the average inter pulse interval, E(t

−t

i−1

Finally, by combining (12c) and (13) we get:

α ≤P

pulse

≤ 1 − R(1 − α). (15a)

Now we compute bounds on relay reliability i.e

≤ R ≤ R

as:

spike

1 + (1 − α)P

spike

≥ R ≥ α · P

spike

. (16)

From (16) and (13), one can see that if T >> T

then R

→ R

→ P

spike

. This result is intuitive because

if pulses in r(t) occur at a slow rate, then the solution

of (1) has enough time to return to the orbit tube after

each pulse. Therefore, P

pulse

, P(X(t) ∈ X

) → 1 and

hence R → P

spike

3 RESULTS

In this section, we will apply (16) to (1).

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

436

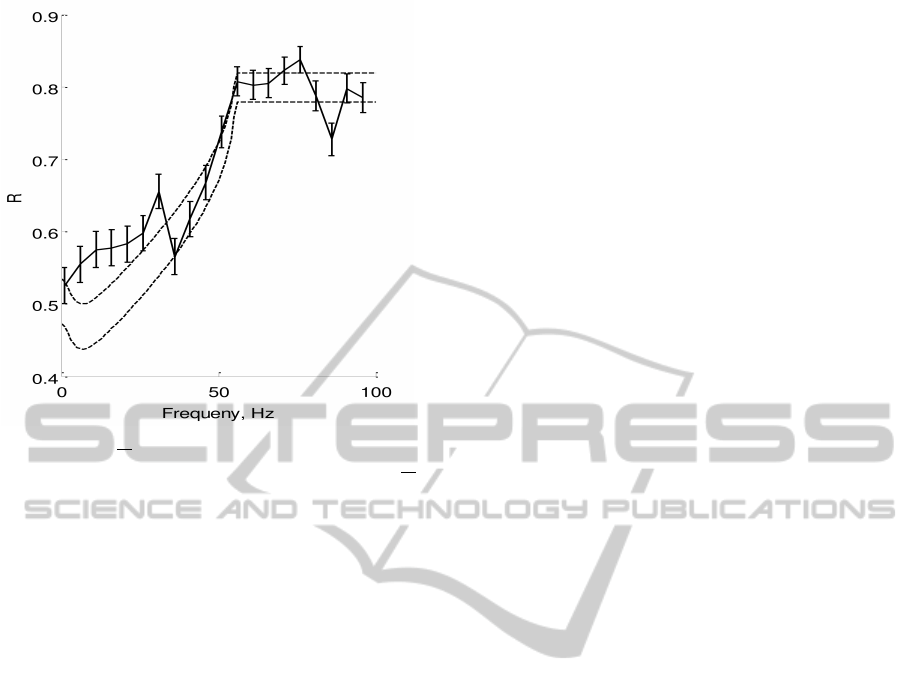
Figure 3: R vs

2π

for the 3

order model - Plots the-

oretical and numerically computed reliability versus

2π

with c

= 0.015, c

= 0.075, I

= 6.5, T

= 105ms, T

80ms,T = 180ms. Dotted lines are lower and upper bounds

on reliability from the (16). Solid line is plotting R

emp

cal-

culated by running simulation of (1), error bars show ±std.

We estimated I

= 6 as the minimum hieght of a r(t) pulse,

that make the neuron spike.

In Figure 3, we plot our reliability bounds (16)

along with reliability computed numerically through

simulation of the 3rd order model. We see that our

bounds predict the reliability well except for some er-

rors in the low frequency range. This is due to the fact

that we did not consider higher order dynamics of the

order model. However, our bounds qualitatively

predict the trend of reliability well even for the higher

order model.

In general, our analytical bounds are applicable to

higher dimensional models as long as the model 1.

does not generate a spike if there is no pulse in r(t),

and 2. has a threshold behavior. The second condi-

tion is true for most of neurons that satisfy the ﬁrst

condition. Our analysis may also be extended to in-

clude neurons that spike without any driver input, but

in this manuscript we neglect such dynamics.

4 DISCUSSION

In this manuscript, we studied the reliability of a relay

neuron. A relay neuron receives two inputs: a driving

input, r(t), and a modulating input, u(t). The neuron

generates one output, V (t), which relays r(t) condi-

tioned on u(t). Our goal was to precisely determine

how the modulating input impacts relay reliability. To

calculate relay reliability, we used LTI systems theo-

retic tools to derive the analytical bounds (16) on relay

reliability as a function of different input and model

parameters. Speciﬁcally, (16) implies that if the mod-

ulating input is of the form u(t) = c

sin(ωt), then

increasing c

or c

decreases reliability. However, in-

creasing ω increases reliability. In addition, our reli-

ability curve (see Figure 3) suggests that on increas-

ing ω, reliability ﬁrst increases slowly and then in-

creases rapidly and plateaus. (16) is powerful as it

characterizes the multiple dependencies of reliability

on u(t), r(t) and relay neuron model parameters. Fur-

thermore, analytic bounds from (16) contain results

obtained through simulation of the 3

order models

of a relay neuron. Our bounds captured reliability

under both the depolarized and hyperpolarized (not

shown due to limited space) states of the 3rd order

neuron and shows the generality of our analysis.

REFERENCES

Agarwal R. and Sarma S. V. (2011). The effects of dbs

patterns on basal ganglia activity and thalamic relay. J

Comput Neurosci, (accepted for publication).

Bekisz M. and Wrobel A. (1999). Coupling of beta and

gamma activity in corticothalamic system of cats at-

tending to visual stimuli. NeuroReport, 10:3589–94.

Erwin E., Baker F. H., Busen W. F., and Malpeli J. G.

(1999). Relationship between laminar topology and

retinotopy in the rhesus lateral geniculate nucleus: re-

sults from a functional atlas. J.Comp neurol, 407:92–

102.

FitzHugh R. (1955). Mathematical models of threshold phe-

nomena in the nerve membrane. Bulletin of Mathe-

matical Biology, 17(4):257–278.

Greenstied Charles M. and Snell J. Laurie (2003). Introduc-

tion to Probability. American Mathematical Society.

Guillery R. W. and Sherman S. M. (2002). Thalamic relay

functions and their role in corticocortical communica-

tion: Generalizations from the visual system. Neuron,

33:163–176.

Guo Y., Rubin J. E., McIntyre C. C., Vitek J. L., and Ter-

man D. (2008). Thalamocortical relay ﬁdelity varies

in deep brain stmulation protocols in data-driven com-

putational models. J. Neurophysiol., 99:1477–1492.

Hirsch J. C., Fourment A., and Marc M. E. (1983). Sleep-

related variations of membrane potential in the lateral

geniculate body relay neurons of the cat. Brain Re-

search, 259(2):308–312.

Hughes S. W., Lorincz M., Cope D. W., Blethyn K. L.,

Kekesi K. A., Parri H. R., Juhasz G., and Crunelli V.

(2004). Synchronized oscillations at α and θ frequen-

cies in the lateral geniculate nucleus. Neuron, Vol. 42,

253268, April 22, 2004,.

Kastner S., Schneider K. A., and Wunderlich K. (2006).

Chapter 8 beyond a relay nucleus: Neuroimaging

UsingLinearSystemsTheorytoStudyNonlinearDynamicsofRelayCells

437

views on the human lgn. Progress in Brain Research,

155 Part B:125–143.

Lagier Samuel , Carleton Alan, and Lledo Pierre-Marie

(2004). Interplay between local gabaergic interneu-

rons and relay neurons generates γ oscillations in

the rat olfactory bulb. The Journal of Neuroscience,

24(18):4382–4392.

Lodish H., Berk A., and Zipursky S. L. (2000). Molecular

Cell Biology. 4th edition. W. H. Freeman.

Logothetis N. K. (2002). The neural basis of blood oxygen

level dependent functional magnetic resonance imag-

ing signal. Phil. Trans R. Soc. Lond B, 357(1003-37).

Lorincz M. L., Kekesi K. A., Juhasz G., Crunelli V., and

Hughes S. W. (2009). Temporal framing of thalamic

relay-mode ﬁring by phasic inhibition during the al-

pha rhythm. Neuron, 63:683–96.

Manor Y., Rinzel J., Segav I., and Yarom Y. (1997). Low

amplitude oscillations in inferior olive: A model based

on electrical coupling of neurons with heterogeneous

channel densities. J. Neurophysiol.

Masson G. L., Masson S. R. L., D., and Bal T. (2002). Feed-

back inhibition controls spike transfer in hybrid thala-

mic circuits. Nature, 417:854–858.

O’Connor D. H., Fukui M. M., Pinsk M. A., and Kastner

S. (2002). Attention modulates responses in the hu-

man lateral geniculate nucleus. nature neuroscience,

5(11):1203–1209.

Platkiewicz J. and Brette R. (2010). A threshold equa-

tion for action potential initiation. PloS Comput Biol,

6(7):1000850.

Reinagel P., Godwin D., Sherman M., and Koch C. (1999).

Encoding of visual information by lgn bursts. Journal

of Neurophysiology, 81:2558–69.

Rubin J. and Josic K. (2007). The ﬁring of an excitable

neuron in the presence of stochastic trains of strong

synaptic inputs. Neural Computation, 19:1251–1294.

Rubin J. E. and Terman D. (2004). High frequency stimula-

tion of the subthalamic nucleus eliminates pathologi-

cal thalamic rhythmicity in a computational model. J.

Comput. Neurosci., 16(3):211–35.

Seki Kazuhiko, Perlmutter Steve I., and Fetz Eberhard E.

(2003). Sensory input to primate spinal cord is presy-

naptically inhibited during voluntary movement. Na-

ture Neuroscience, 6:1309–1316.

Sherman S. M. (2007). The thalamus is more than just a

relay. Current Opinion in Neurobiology, 17(4):417–

422.

Sherman S. M. and Guillery R. W. (1998). On the actions

that one nerve can have on another: Distinguishing

”drivers” from ”modulators”. PNAS, 95(12):7121–26.

Sherman S. M. and Guillery R. W. (2002). The role of the

thalamus in the ﬂow of information to the cortex. Phil.

Trans. R. Soc. Lond. B., 357(1428):1695–1708.

Sohal V. and Huguenard J. (2002). Reciprocal inhibition

controls the oscillatory state in thalamic networks.

Neurocomp, 44:653–659.

Sohal V., Huntsman M., and Huguenard J. (2000). Recipro-

cal inhibitory connections regulate the spatiotemporal

properties of intrathalamic oscillations. J Neurosci,

20:1735–1745.

Wolfart J., Debay D., Masson G. L., Destexhe A., and

Bal T. (2005). Synaptic background activity controls

spike transfer from thalamus to cortex. Nature Neuro-

science, 8(12):1760–1767.

Zhan X., Cox C., Rinzel J., and Sherman S. (1999). Current

clamp and modeling studies of lowthreshold calcium

spikes in cells of the cats lateral geniculate nucleus. J.

Neurophysiol, 81:2360–2373.

APPENDIX

Table 1: Parameters and functions for (1).

∞

(V )

(1+exp(−(V+37)/7))

∞

(V )

(1+exp(−(V+60)/6.2))

(V )

0.128exp(−

46+V

)+4/(1+exp(−

23+V

))

∞

(V )

(1+exp((V+41)/4))

∞

(V )

(1+exp((V+84)/4))

(V ) 0.4(28 + exp((V + 25)/(−10.5)))

syn

−85,50mV

−90,−70, 0mV

3,5

0.05,5

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

438