
Supplier Selection based on Process Yield for LED Manufacturing
Processes
Y. T. Tai
1
and Chien-Wei Wu
2
1
Department of Information Management, Kainan University, Taoyuan, Taiwan, R.O.C.
2
Department of Industrial Management, National Taiwan University of Science and Technology, Taipei, Taiwan, R.O.C.
Keywords: Supplier Selection, Yield, Multiple Characteristics, LED.
Abstract: In today’s fierce competitive business environment, it is very essential to work with right suppliers in the
supply chain systems. Consequently, supplier selection problem is very important and has received
considerable attention. In the supplier selection problem, quality is the most popular criterion. In the paper,
we consider a supplier selection problem of comparing two suppliers and selecting the one that has a
significantly higher process capability for the light emitting diode (LED) assembly process with multiple
characteristics. Testing hypotheses for the LED assembly supplier selection are presented. For practitioners’
convenience, the corresponding critical values for the supplier selection in LED assembly process are
tabulated. For illustration purpose, an application is presented.
1 INTRODUCTION
In today’s fierce competitive business environment,
to provide high-quality products, it is very essential
to work with right suppliers in the supply chain
systems. Consequently, the success of a supplier
chain is highly dependent on selection of good
suppliers (Ng, 2008). In the last decades, the
supplier selection problems have been investigated
extensively. Various decision making approaches
have been proposed to tackle the problem. The first
investigation for the supplier selection problem is
presented by Dickson (1966). He identified over
twenty supplier attributes and ranked their
importance, such as quality, net price, and service.
In addition, Degraeve et al., (2000), De Boer et al.,
(2001) reviewed the literature up to 2000. Recently,
Aissaoui et al., (2007) provided a literature review
that covers the entire purchasing process involving
parts and services outsourcing activities. Ho et al.,
(2010) reviewed the papers from 2000 to 2008 and
provided some recommendations for related future
work among various supplier selection methods.
From the extensive investigations on the supplier
selection problem, Ho et al., (2010) summarized
popular criteria including quality, delivery,
price/cost, manufacturing capability, service,
management, technology, research and development,
finance, flexibility, reputation, relationship, risk, and
safety and environment. It should be noted that
quality is the most popular one for the supplier
selection problem in the investigation of Ho et al.
(2010). In most of high-tech manufacturing
industries, process yield has been the most basic and
common quality criterion for measuring process
performance. Process yield is defined as the
percentage of processed product unit passing
inspection. That is, the process characteristic must
fall within the manufacturing tolerance. Due to
fierce competition on consumption products, the
high-tech manufacturing processes require very low
fraction of defectives in parts per million (ppm).
Consequently, it can be found in the literature
reviewed by Ho et al., (2010), the criterion of
acceptable parts per million is a critical quality
related attribute. However, if we make decision only
based on the values of acceptable parts per million
provided by individual supplier, the unreliable
supplier selection decision may be made.
In this paper, we investigate a case of supplier
selection problem regarding a material part of light
emitting diode (LED) assembly that is the critical
devices in smart phones. It should be noted that the
manufacturing process of LED assembly require
very low fraction of defectives in parts per million
(ppm). Consequently, process capability indices
(PCIs) methods are effective to evaluate the non-
conformation of the units produced from a
594
Tai Y. and Wu C..
Supplier Selection based on Process Yield for LED Manufacturing Processes.
DOI: 10.5220/0003987705940598
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (OMDM-2012), pages 594-598
ISBN: 978-989-8565-22-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
manufacturing process and to obtain the
corresponding process yield.
In this paper, we presented an exact process
capability index with multiple characteristics for the
supplier selection problem in a LED case. The
testing hypotheses for the light emitting diode
assembly supplier selection are presented. For
practitioners’ convenience, the corresponding
critical values for the supplier selection in LED
assembly process are also computed and tabulated.
The supplier selection method which is applied in
the LED assembly process is practical and useful for
practitioners and factory in-plant applications.
2 LIGHT EMITTING DIODE
ASSEMBLY PROCESS
In this case, we provide an effective test to check
whether the new supplier can provide better process
yield than the existing supplier. It should be noted
that LED backlight modules involve many attracting
characteristics such as power-saving, wide color
gamut, high dimming ratio, long lifetime, and high
brightness. They have been widely applied in
portable devices and computer monitors. A LED
backlight module is a critical light source for liquid
crystal display (LCD) panels since LCD panels
cannot luminesce themselves. When the smart phone
manufacturers select their suppliers for the LED
assembly on the LED backlight module (see Figure
1), those popular criteria summarized by Ho et al.
(2010) are considered. However, quality is a very
important consideration in the real selection
processes. It should be noted that the industrial
practitioners commonly use C
pk
to assess the process
capability. The index C
pk
only provides an
approximate rather than an exact measure of the
process yield. In addition, C
pk
is restricted to
processes with single characteristic. However, in
LED assembly process, some critical quality
characteristics are considered simultaneously since
these quality characteristics may affect the yield of
the finished goods. Thus, in the paper, to access
exact process yield measure in supplier selection
process, we consider the application of statistical
selection processes based on the process capability
index with multiple characteristics.
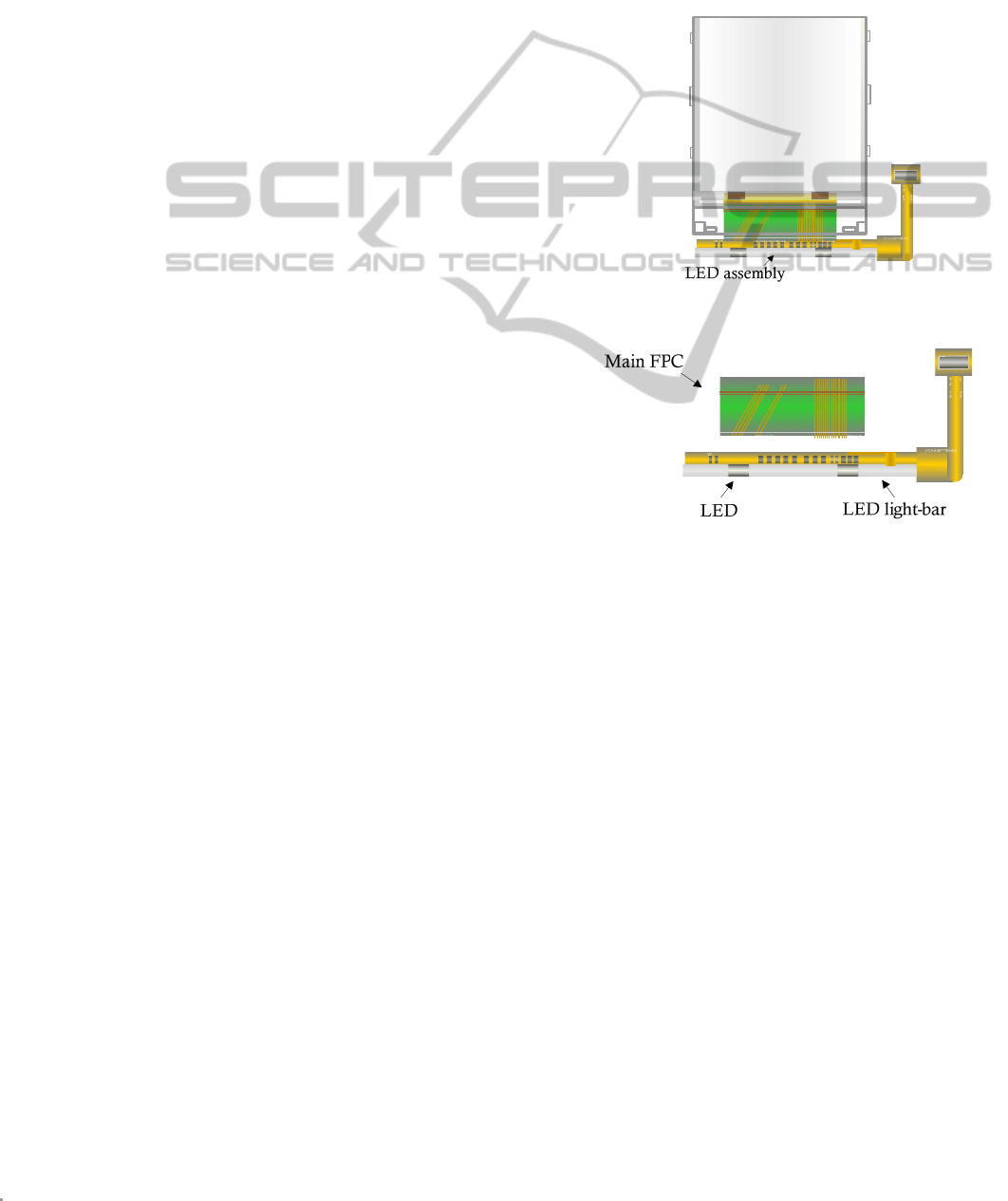
In the LED assembly process, LEDs are bonded
on the FPC (flexible printed circuit) and are referred
to as LEDs light-bar (see Figure 2). It is noted that
there are multiple characteristics are very critical and
should be considered when we evaluate and select
the suppliers. One of the essential characteristics is
the distances between two neighboring LEDs, since
the distance may cause different maximum
uniformities. However, the optical performance
issue is very important. In addition, the LED
assembly is extremely thin and need to connect with
other components. The characteristic of the length of
LED assembly is also critical since it may cause the
situation of unexpected shut-down. Consequently,
the length of the LED assembly should not fall
outside the specification intervals.
Figure 1: LED assembly on a backlight module.
Figure 2: LED light-bar in a LED assembly.
3 SUPPLIER SELECTION BASED
ON PROCESS CAPABILITY
INDEX APPROACH
The most commonly used process capability indices,
C
p
and C
pk
are discussed in Kane (1986). More-
advanced indices C
pm
and C
pmk
are developed by
Chan, Cheng and Spiring (1988) and Pearn, Kotz
and Johnson (1992). Many authors have promoted
the use of various PCIs for evaluating a supplier’s
process capability. Based on analyzing the PCIs, a
production department can trace and improve a poor
process so that the quality level can be enhanced and
the requirements of the customers can be satisfied.
However, the index C
pk
can only provide an
approximation rather than an exact measure on the
SupplierSelectionbasedonProcessYieldforLEDManufacturingProcesses
595

process yield. To obtain an exact measure, Bolyes
(1994) considered a yield index, referred to as S
pk
for normally distributed processes. The index S
pk
is
defined as:
1
11 1
32 2
pk
USL LSL
S
μμ
σσ
−
⎧− −⎫
⎛⎞⎛⎞
=Φ Φ +Φ
⎨⎬
⎜⎟⎜⎟
⎝⎠⎝⎠
⎩⎭
,
where
USL and LSL are the upper and the lower
specification limits, respectively,
μ
is the process
mean, and
σ
is the process standard deviation.
To make more reliable supplier selection
decision, some existing research works have been
presented to perform the effective test. Pearn et al.,
(2004) presented a supplier selection procedure
based on the index C
pm
which can tackle a process
with single characteristic. Wu et al., (2008) applied
the bootstrap method and recommended a procedure
for assessing capability index C
pk
to solve supplier
selection problems. Pearn et al., (2011) provided an
effective powerful test for one-sided supplier
selection problem. Lin and Pearn (2010) considered
the process selection problem by using the yield
index S
pk
to compare two production processes and
select one that has higher process yield. However,
factory practitioners usually consider a process with
multiple characteristics for supplier selection
decisions, particularly, in the LED assembly process.
In this paper, we consider the exact yield index
T
p
k
S and apply the proposed supplier selection
method with multiple characteristics for the light
emitting diode assembly process to help the
participators to make more reliable decisions for
supplier selections.
3.1 Supplier Selection Bases on
T
pk
S
To obtain accurate yield assessment for processes
with multiple characteristics, multiple characteristics
should be considered simultaneously for the LED
assembly processes. In the paper, we apply the
process capability index
T
p
k
S which was proposed by
Chen et al., (2003) and can be defined as follows.
1
1
11
(2 (3 ) 1) 1 ,
32
v
T
pk pki
i
SS
−
=
⎧⎫
⎡⎤
=Φ Φ −+
⎨⎬
⎢⎥
⎣⎦
⎩⎭
∏
where
p
ki
S denotes the
p
k
S value of the ith
characteristic for i= 1, 2, . . . , v, and v is the number
of characteristics. The index can be viewed as a
generalization of the single characteristic yield
index,
p
k
S
.
Since the index
T
p
k
S
provides an exact measure
on the process yield of multinormal processes in
which the characteristics are mutually independent
(Pearn and Cheng, 2010). Pearn and Cheng (2010)
displayed various commonly used capability
requirements and the corresponding production as
well as non-conformities in ppm in Table 1.
Table 1: Various commonly used capability requirements
and the corresponding production as well as non-
conformities in ppm.
T
p
k
S
Yield NCPPM
1.00 0.997300204 2699.796
1.20 0.999681783 318.217
1.40 0.999973309 26.691
1.60 0.999998413 1.587
1.80 0.999999933 0.067
2.00 0.999999998 0.002
3.2 Statistical Test for Supplier
Selection
In this paper, we apply a powerful approach for
supplier selection. Suppose that the process yield
requirement by
T
p
k
S for given processes is C, and the
current supplier has reach the yield requirement. In
real applications, the supplier replacement is time
consuming and costly since the validation of a new
process is complicated. Consequently, when we find
a new supplier to compete with the current supplier,
we can consider the following hypothesis testing to
test whether the new supplier can provide
convincing information to claim that its process
yield is higher than the current supplier. The
considered hypothesis testing for comparing the two
T
p
k
S values: H
0
:
1
T
p
k
S ≥
2
T
p
k
S versus H
1
:
1
T
p
k
S <
2
T
p
k
S
(or equivalently, H
0
:
2
T
pk
S −
1
T
p
k
S ≤ 0 versus H
1
:
2
T
pk
S
−
1
T
p
k
S >0). The test statistic W can be
expressed as
2
ˆ
T
pk
S
−
1
ˆ
T
p
k
S .
4 A LED APPLICATION
To demonstrate the applicability of the supplier
selection method, we consider a case for light
emitting diode assembly process. In the case, two
essential quality characteristics are considered
simultaneously. As described in Section 2, the
distances between two neighboring LEDs and the
length of LED assembly are the two critical quality
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
596

characteristics for supplier selection. In the case, the
LED assembly products require a minimal
capability. The minimal requirement of the LED
assembly characteristic is
T
p
k
S = 1.20.
For the product type we investigated, the upper
and lower specification limits of the distance
between LEDs are set to 12.2 and 15.4 millimeter. In
addition, the upper and lower specification limits of
the length of LED assembly are set to 19.5 and 21.5
millimeter. The millimeter is used as the unit for the
two specifications.
To determine whether the new Supplier (Supplier
II) provides a better process capability of the LED
assembly products than current Supplier (Supplier I),
we perform the hypothesis testing:
02 1
:
TT
p
kpk
H
SS≤
versus
12 1
:
TT
p
kpk
H
SS> . We collected two data sets
from suppliers I and II with
1
n =
2
n =100. Based on
the observations, we compute the sample estimate
ˆ
T
p
k
S of
T
p
k
S
for both suppliers. The sample average
(
j
x
), sample standard deviation (
j
s
) and
ˆ
p
kj
S for
each characteristic are also calculated. Thus, we can
obtain that
1
ˆ
T
p
k
S = 1.104 and
2
ˆ
T
p
k
S =1.415.
We calculated the test statistic W =
2
ˆ
T
pk
S
−
1
ˆ
T
p
k
S =
0.311 for the proposed supplier selection method. In
the paper, we used a commercial computation
software to compute the critical value (see Table 2)
that is very useful to help us to make the decision for
the hypothesis testing.
The input parameters of the
program involving the values of
1
T
p
k
S
,
2
T
p
k
S
,
the
corresponding sample sizes n
1
, n
2
, C, and α.
Table 2: Critical values for rejecting
21
TT
p
kpk
SS≤ with
12
nn= =30(10)100 and
α
=0.05.
n
12
TT
pk pk
SSC
=
=
1.0 1.2 1.4 1.6
30 0.3003 0.3604 0.4204 0.4805
40 0.2601 0.3121 0.3641 0.4161
50 0.2326 0.2791 0.3257 0.3722
60 0.2123 0.2548 0.2973 0.3398
70 0.1966 0.2359 0.2752 0.3146
80 0.1839 0.2207 0.2575 0.2942
90 0.1734 0.2081 0.2427 0.2774
100 0.1645 0.1974 0.2303 0.2632
In the case, we use the Pearson-Correlation test
to justify the correlation. The result shows the
relationship among the two characteristics can be
regarded as independent. In addition, we run the
developed program with
1
n =
2
n =100,
12
TT
p
kpk
SS= =1.20, and α= 0.05 to obtain the critical
value as 0.1974 for the presented supplier selection
method (it also can be found in Table 2).
Since the testing statistic W = 0.311 > 0.1974, we
can conclude that the new supplier is superior than
the current supplier with 95% confidence level.
5 CONCLUSIONS
Supplier selection problem in light emitting diode
assembly process is very important and frequently
occurred. Since the multiple characteristics should
be considered in the light emitting diode (LED)
assembly process for supplier selection, in the paper,
we presented and applied a supplier selection
method based on process yield index to provide
exact measures on process yield with multiple
characteristics. For users’ convenience in applying
the supplier selection method in LED assembly
process, the critical values of the hypothesis testing
with various sample sizes are presented and
tabulated. The supplier selection method which is
applied in the LED assembly process is very useful
for factory in-plant applications.
ACKNOWLEDGEMENTS
The authors would like to express their gratitude to
the anonymous referees for their valuable comments
and careful readings, which greatly improved the
presentation of this paper. This paper was supported
in part by the National Science Council, Taiwan,
ROC, under the contracts NSC 100-2410-H-424-011
and NSC 100-2628-E-011-013-MY3.
REFERENCES
Aissaoui, N., Haouari, M., Hassini, E., (2007). Supplier
selection and order lot sizing modeling: A review.
Computers & Operations Research, 34, 3516-3540.
Boyles, R. A., (1994). Process capability with asymmetric
tolerances. Communication in Statistics: Simulation
and Computation, 23(3), 615-643.
Chan, L. K., Cheng, S. W., Spiring, F. A., (1988). A new
measure of process capability Cpm. Journal of Quality
Technology, 20(3), 162-175.
Chen, K. S., Pearn, W. L., Lin, P. C., (2003). Capability
measures for processes with multiple characteristics.
Quality and Reliability Engineering International,
19(2), 101-110.
Degraeve, Z., Labro, E., Roodhooft, F., (2000). An
SupplierSelectionbasedonProcessYieldforLEDManufacturingProcesses
597

evaluation of supplier selection methods from a total
cost of ownership perspective. European Journal of
Operational Research, 125(1), 34-58.
De Boer, L., Labro, E., Morlacchi, P., (2001). A review of
methods supporting supplier selection. European
Journal of Purchasing and Supply Management, 7(2),
75-89.
Dickson, G. W., (1966). An analysis of vendor selection
systems and decisions. Journal of Purchasing, 2, 5-17.
Ho, W., Xu, X., Dey, P. K., (2010). Multi-criteria decision
making approaches for supplier evaluation and
selection: A literature review, European Journal of
Operational Research, 202, 16-24.
Kane, V. E., (1986). Process capability indices. Journal of
Quality Technology, 18(1), 41-52.
Lin, C. J., Pearn, W. L., (2010). Process selection for
higher production yield based on capability index Spk.
Quality and Reliability Engineering International, 26,
247–258.
Ng., W. L., (2008). An efficient and simple model for
multiple criteria supplier selection problem. European
Journal of Operational Research, 186, 1059-1067.
Pearn, W. L., Cheng, Y. C., (2010). Measuring production
yield for processes with multiple characteristics.
International Journal of Production Research, 48(15),
4519-4536.
Pearn, W. L., Kotz, S., Johnson, N. L., (1992).
Distributional and inferential properties of process
capability indices. Journal of Quality Technology,
24(4), 216-233.
Pearn, W. L., Wu, C. W., Lin, H. C., (2004). Procedure for
supplier selection based on Cpm applied to super
twisted nematic liquid crystal display processes.
International Journal of Production Research, 42(13),
2719-2734.
Pearn, W. L., Hung, H. N., Chuang, Y. S., Su, R. H.,
(2011). An effective powerful test for one-sided
supplier selection problem. Journal of Statistical
Computation and Simulation, 81(10), 1313-1331.
Wu, C. W., Shu, M. H., Pearn, W. L., Liu K. H., (2008).
Bootstrap approach for supplier selection based on
production yield. International Journal of Production
Research, 46(18), 5211-5230.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
598
