Emotion Recognition of Violin Music based on Strings Music

Theory for Mascot Robot System

Z.-T. Liu

1, 2

, Z. Mu

, L.-F. Chen

1, 2

, P. Q. Le

, C. Fatichah

, Y.-K. Tang

, M. L. Tangel

, F. Yan

K. Ohnishi

, M. Yamaguchi

, Y. Adachi

, J.-J, Lu

, T.-Y. Li

, Y. Yamazaki

F.-Y. Dong

and K. Hirota

Department of Computational Intelligence and Systems Science, Tokyo Institute of Technology,

G3-49, 4259 Nagatsuta, Midori-ku, Yokohama, 226-8502, Kanagawa, Japan

School of Information Science and Engineering, Central South University,

Yuelu Mountain, Changsha, 410083, Hunan, China

Department of Electrical, Electronic, and Information Engineering, Kanto Gakuin University,

1-50-1 Mutsuura-higashi, Kanazawa-ku, Yokohama, Kanagawa 236-8501, Japan

Keywords: Emotion Recognition, Violin, Music, Support Vector Regression, Fuzzy Logic.

Abstract: Emotion recognition of violin music is proposed based on strings music theory, where the emotional state of

violin music is expressed by Affinity-Pleasure-Arousal emotion space. Besides the music features from

audio processing, three features (i.e., left-hand feature, right-hand feature, and dynamics) with regard to

both composition and performance of violin music, are extracted to improve the emotion recognition of

violin music. To demonstrate the validity of this proposal, a dataset composing of 120 pieces of author-

performed violin music with six primary emotion categories is established, by which the experimental

results of emotion recognition using Support Vector Regression report overall recognition accuracy of

86.67%. The proposal could be an integral part for analyzing the communication atmosphere with

background music, or be used by a music recommendation system for various occasions.

1 INTRODUCTION

Music not only helps people edify sentiment, but

also plays an important role in psychotherapy such

as elimination of stress and mood shift. Music

emotion that is the feelings of audience inspired by

music, therefore, has gradually recevied as much

attention as human emotion. In music psychology,

music is able to affect the feeling of listeners

(Hargreaves, 1999). For example, when a person is

sleepy, strong rhythm music could refresh him/her

and decrease drowsiness; on the contrary, a lullaby

helps children fall to sleep, all of which demonstra-

tes the importance of music in generating emotions.

Recently, there are mainly two types of emotion

recognition of audio signals, i.e., speech emotion

recognition

(Ayadi et al., 2011) and music emotion

recognition (Kim, 2010), where the study of music

emotion always focuses on extraction of features

from audio processing such as intensity features,

timbre features, rhythm features (Lu, et al., 2006).

Another two important emotion-related components

– composition and performance of music, however,

are seldom used for music emotion recognition, and

both of them are associated with music theory.

Music is a broad concept that includes different

types, e.g., classical music, folk music, rock music,

opera music, and others. Music can be performed by

various instruments all around the world, for

example, violin, cello, piano, guitar, trumpet, flute,

drum, and so on. A general model of music emotion,

therefore, is not easy to create. Instead, study on

emotion recognition of particular types of music or

music performed by one kind of instrument should

be taken into account.

Classical music is the most typical type of music

worldwide, in which the elements of music such as

melody, harmony, and rhythm are all well-balanced.

Furthermore, it is an ideal object of study for

emotion recognition because of its richness of

emotions. To play the classical music, violin, a four-

string instrument tuned in perfect fifths, is the best

Liu Z., Mu Z., Chen L., Le P., Fatichah C., Tang Y., Tangel M., Yan F., Ohnishi K., Yamaguchi M., Adachi Y., Lu J., Li T., Yamazaki Y., Dong F. and Hirota

K..

Emotion Recognition of Violin Music based on Strings Music Theory for Mascot Robot System.

DOI: 10.5220/0003991500050014

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 5-14

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

choice since it is recognized as the melodic

backbone of most classical music (Starks, 2012) and

plays a leading role in emotion expression.

Emotion recognition of violin music based on

strings music theory is proposed to realize casual

communication between humans and robots in

Mascot Robot System (MRS). In the MRS, both

speech emotion recognition and music emotion

recognition are implemented, using Affinity-

Arousal-Pleasure emotion space to describe the

emotional states. In addition, for many-to-many

communication, multiple emotional states including

humans, robots, and background music are taken

into consideration for analyzing communication

atmosphere which is defined as Fuzzy Atmosfield

(Liu et al., 2011).

In terms of the relationship between the

characteristics of the violin music and the feelings of

audiences, three features of violin music including

left-hand feature based on “Just Intonation”, right-

hand feature based on metronome, and dynamics

based feature are proposed, which are closely

associated with the three attributes of emotion space,

respectively. Inspired from this idea, three sets of

features, namely, harmony, rhythm, and dynamics as

the extension of the proposed features are extracted.

Six basic emotion categories, i.e., happiness,

sadness, comfort, disgust, anxiety, and surprise are

adopted for emotion representation of violin music.

A dataset of 120 pieces of violin music played by

the author is established for the experiment. Support

Vector Regression (SVR) is employed for training

the emotion model with 60 pieces of violin music,

and other 60 pieces are used for testing. The

experimental results confirm the validity and

availability of the proposal.

In 2, a brief overview of the Mascot Robot

System is given. Emotion recognition of violin

music based on strings music theory and Support

Vector Regression is proposed in 3. In 4,

experiments on emotion recognition of violin music

and the application to background music selection

for home party scenarios are presented.

2 MASCOT ROBOT SYSTEM

Mascot Robot System is an information presentation

system within a networked robotic environment

(Hirota and Dong, 2008), where robots facilitate a

smooth and harmonious communication atmosphere

with humans.

2.1 Framework of Mascot Robot

System

The MRS has been composed of four fixed eye

robots and one mobile eye robot (each eye robot

equipped with speech recognition module (SRM),

emotion synthesis module, and emotion recognition

module), an information recommendation server,

and a system server that is responsible for overall

management, as shown in Fig. 1.

Figure 1: Framework of Mascot Robot System.

Using the emotion synthesis module, eye robots

are able to express emotions based on the

mechanisms of the human eye. Robot Technology

middleware (RT Middleware) is used to connect

among the system’s components. With RT

middleware, each robot can be viewed as a

networked component and the whole system can be

managed from the view point of service level

(Yamazaki et al., 2010).

Server

Robot 2

Robot 1

Robot 3

Robot 5

Robot 4

door

window

Server

Robot 2

Robot 1

Robot 3

Robot 5

Robot 4

door

window

Server

Robot 2

Robot 1

Robot 3

Robot 5

Robot 4

door

window

Figure 2: Household environment for human-robot

communication.

Fig. 2 shows a household environment that is

created for testing the MRS, where four fixed eye

robots are placed on the TV, a dart game machine, an

information terminal, and a mini-bar. The mobile eye

robot accompanies and assists the users with

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

emotion expression by eye movement and voice

communication.

2.2 Fuzzy Atmosfield for Analyzing

Communication Atmosphere

For many-to-many communication, only emotion

analysis is not enough for atmosphere understanding.

Fuzzy Atmosfield (FA), therefore, is used to

describe mood states among communicators being

generated from not only the verbal and non-verbal

information of speakers, but also background music

or noise (Liu et al., 2011).

Besides the emotional states of individuals in the

communication, environmental factors such as

music are essential factors for the FA in a real life

environment. As an independent emotional object,

the emotional state of background music is defined

as M in the function of the FA (Liu et al., 2011),

( ( ), , ( ), ( )), 1

() (1 ) ( 1) ( (), ,

(), ()), 1

fEt Et Mt t

FA t FA t f E t

Et Mt t

λγλ

⋅⋅⋅ =

= − − ⋅ + ⋅⋅⋅

⎧

⎪

⎨

⎪

⎩

(1)

where FA is the atmosphere state of the Fuzzy

Atmosfield; f is the function of emotional states of E

and M at time t, using fuzzy logic and weighted average

method; E

is the emotional state of the ith individual,

i=1, …, n; M is the emotional state of the

background music;

is the correlation factor,

≤≤; and

is a monotonically decreasing

function. In the MRS, Affinity-Pleasure-Arousal

emotion space is used for the emotion representation

of humans, robots, and background music.

2.3 Affinity-Pleasure-Arousal Emotion

Space

The Affinity-Pleasure-Arousal emotion space is used

to illustrate the emotional state of violin music. By

using this emotion space, it is not only possible to

express fixed emotional states but also to take into

account rapid variations in the emotional state due to

time involving music performance (Yamazaki et al.,

2008), as shown in Fig. 3.

The “Affinity” axis represents the degree of

empathy, i.e., intimacy (positive affinity) and

estrangement (negative affinity); the “Pleasure-

Displeasure” axis means happiness (positive values)

and sadness (negative values); and the “Arousal-

Sleep” axis expresses excitement (positive values)

and calm (negative values).

To compute the emotional states of violin music

Pleasure

Displeasure

Arousal

Sleep

Affinity

(1)Et−

()Et

(1)Et+

Figure 3: Affinity-Pleasure-Arousal emotion space.

in each axis of Affinity-Pleasure-Arousal emotion

space, two steps should be implemented:

 The features of violin music that are related to

each attributes (i.e., axis) of emotion space

should be extracted and selected;

 Regression method should be used for training

the relationship between attributes of emotion

space and features of violin music.

3 EMOTION RECOGNITION OF

VIOLIN MUSIC

3.1 Features of Violin Music

based on Strings Music Theory

To define the features of violin music, left-handed

fingering is taken as an example for emotion

recognition of violin music in this paper.

Three basic elements of music, i.e., pitch, length,

and strength, are highly associated with the

attributes of the Affinity-Pleasure-Arousal emotion

space. In violin music, the pitch varies when left

hand fingers press the strings, for which the feature

of pitch-related melody is named as left-hand feature;

in addition, tempo-related feature is defined as right-

hand feature since the music speed is correlated with

right hand control of violin bow on the strings; and

the feature based on dynamics is defined for

representing the strength.

3.1.1 Left-hand Feature

based on “Just Intonation”

The left-hand feature is defined according to the

music theory of “Just Intonation” (Barbour, 2004).

The violin has four strings which show the common

G-D-A-E tuning in the case of open strings.

Adjacent strings, in musicology, are defined as a

pitch of “perfect fifth” in Fig. 4.

EmotionRecognitionofViolinMusicbasedonStringsMusicTheoryforMascotRobotSystem

Figure 4: Perfect fifth of open strings.

The major third is obtained by adding another

note in the middle of a perfect fifth. Diatonic scale

can be obtained by adding a note in the middle of

major third with the addition of pure intervals, as

shown in Fig. 5.

Figure 5: Full scale of interval.

Semitone is defined as the smallest unit of

Western music, and it is possible to determine the

number of semitones in the interval between two

Table 1: Representation of interval.

Staff Interval

Number

semitone

Ratio

between

frequencies

unison 0 1:1

minor

second

1 16:17

major

second

2 8:9

minor

third

3 5:6

major

third

4 4:5

perfect

fourth

5 3:4

perfect

fifth

7 2:3

minor

sixth

8 5:8

major

sixth

9 3:5

minor

seventh

10 5:9

major

seventh

11 9:17

octave 12 1:2

notes. Interval, therefore, can be represented by the

number of semitones and the ratio between

frequencies of two notes in Table 1.

The ratio of

is expressed by

log ( )

= ,

(2)

where

[1, 1]

I −∈ . If

I is positive, the melody

changes in the shape of ascending, and the

consonance of interval is increased towards a

positive feeling; on the contrary, if it is negative, the

melody changes in descending shape, and the

consonance of interval is decreased towards a

negative feeling.

Moreover, in musicology, if the interval with one

more semitone and one less semitone than the

“Major” or “Perfect” are defined as “augmented”

and “diminished” (Zweifel, 2005); similarly, two

more semitones and two less semitones are defined

as “doubly augmented” and “doubly diminished”.

For Western music, it is convenient to use the

ratio between frequencies of two notes, whereas it is

better to use the “consonant” interval for emotional

analysis of music in musical psychology. In terms of

this idea, the rules for the relationship between

interval and consonance are formulated as illustrated

in Table 2, where the consonance is classified into

five categories including absolutely consonant,

perfect consonant, relative consonant, imperfect

consonant, and dissonant.

Table 2: Consonance of interval.

Interval Consonance

unison, octave

solutely

consonant

perfect fourth, perfect fifth

erfect

consonant

major third, minor third,

major sixth, minor sixth

relative

consonant

major second, minor second,

major seventh, minor seventh

imperfect

consonant

augmented or doubly augmented,

diminished or doubly diminished

dissonant

The more consonant the interval is, the more

pleasant the audience feels (Sethares, 1993), for

which the consonance of interval is used to calculate

the value of the “Pleasure-Displeasure” axis.

3.1.2 Right-hand Feature

based on Metronome

Metronome is commonly used to maintain a

consistent tempo with steady regular beats for play-

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

ing violin. It is a mechanical device that produces

regular, metrical ticks (beats, clicks), which is

settable in beats per minute (BPM). The BPM is a

unit typically used as a measure of tempo in music.

For example,

= 72 BPM can be represented as

72 quarter notes in a minute. Fig. 6 shows a

metronome with a pendulum-swing.

Figure 6: A photo of metronome from Wikipedia.

To specify the tempo, Grave, Largo, Adagio,

Larghetto, Andante, Andantino, Moderato, Allegre-

tto, Allegro, Vivace, and Presto (Brown, 1999) are

used as shown in Table 3.

Table 3: Common tempo symbols for staff.

Tempo Sign Meaning BPM

Grave slow and solemn 36-46

Largo broadly 46-56

Adagio slow and stately 56-63

Larghetto rather broadly 63-72

Andante at a walking pace 72-80

Andantino slightly faster than andante 80-92

Moderato moderately 92-108

Allegretto moderately fast 108-132

Allegro fast, quickly and bright 132-160

Vivace lively and fast 160-184

Presto very fast 184-208

Generally speaking, the tempo of music

associates closely with perception of audiences

(Juslin, 2000), in particular, a pair of emotional

attributes – arousal and sleep. For example, fast

tempo expresses arousing excitement but slow

tempo inspires inactive mood. The BPM that is

adopted as the right-hand feature, therefore, is used

to determine the emotional states in the “Arousal-

Sleep” axis.

3.1.3 Dynamics based Feature

The dynamics of Western music, not only refers to

the volume, but also refers to the musical expression

by the contrast of different performance methods.

Table 4 shows the words indicating the change of

dynamics (common dynamics signs), namely, pp, p,

mp, mf, f, and ff

(Nakamura, 1987).

Table 4: Common dynamics Symbols for staff.

Dynamics sign Name Meaning

Pianissimo very soft

Piano soft

Mezzo-Piano moderately soft

Mezzo-Forte moderately strong

f Forte strong

Fortissimo very strong

As the intensity of music decreases, the distance

perception is generated, while the degree of empathy

is decreased. For example, when someone is

depressed, he/she often feels lonely, tending to a

negative mood. The features of dynamics (i.e., the

strength of violin music performance), therefore, is

used to estimate the “Affinity” in the emotion space.

3.2 Feature Extraction and Selection

Commonly used features (Kim et al., 2010 and Yang

et al., 2008) for emotion recognition of audio signal

are enumerated in Table 5, which can be

summarized into six types, i.e., harmony, rhythm,

dynamics, articulation, register, and timbre.

For the feature extraction, two free softwares

PsySound (Cabrera, 1999), PRAAT (Boersma and

Weenink, 2008), and a open-source Matlab toolbox

MIRtoolbox (Lartillot and Toiviainen, 2007) are

used.

In the light of the analysis of violin music theory

in 3.1, three sets of features in Table 5, i.e.,

Harmony, Rhythm, and Dynamics, are employed to

compute the values in “Pleasure-Displeasure”,

“Arousal-Sleep”, and “Affinity” axes, respectively.

Table 5: Commonly used audio feature types.

Feature Type

Roughness, Harmonic Change,

Pitch Multiplicity, Dissonance, Key

Clarity, Sharpness, Pure Tonal,

orness

Harmony

Rhythm Strength, Regularity,

Tempo, Beat Histograms

Rhythm

RMS Energy, Loudness, Sound

Pressure Level, Volume, Spectral

Centroi

Dynamics

Event Density, Attack Slope,

Attack Time

Articulation

Chromagra

Chroma Centroid and Deviation

MFCCs, Level, Sharpness,

ectral Sha

e, S

ectral Contrast

Timbre

EmotionRecognitionofViolinMusicbasedonStringsMusicTheoryforMascotRobotSystem

With the addition of the features in 3.1, nine

features of Harmony (i.e., The Ratio between

Frequencies of Two Notes, Roughness, Harmonic

Change, Pitch Multiplicity, Dissonance, Key Clarity,

Sharpness, Pure Tonal, and Majorness), five features

of Rhythm (i.e., BPM, Rhythm Strength, Rhythm

Regularity, Average Tempo, and The Ratio between

Average Peak Strengths and Average Valley

Strengths), and five features of Dynamics (i.e.,

RMS Energy, Loudness, Sound Pressure Level,

Volume, and Spectral Centroid) are selected

empirically for emotion recognition of violin music.

3.3 Emotion Recognition using Support

Vector Regression

Emotion recognition of violin music using Support

Vector Regression is proposed, where the regression

analysis is utilized for analyzing the relationship

between the value of each axis in the Affinity-

Pleasure-Arousal emotion space and emotion-related

features of violin music.

3.3.1 Overview of Emotion Recognition of

Violin Music

In the emotion recognition process, the central task

is to determine the emotional states of violin music

based on the music features mentioned in 3.2 by

using SVR. In addition, all the music features are

normalized for the regression.

The framework of emotion recognition is shown

as Fig. 7, mainly consisting of three steps:

 Training - SVR models are separately trained

for each of the three axes in the emotion

space, namely “Affinity”, “Pleasure-

Displeasure”, and “Arousal-Sleep”. The

features are extracted from the violin music,

and the target values for regression are

obtained through questionnaire survey;

 Testing - For a coming piece of violin music,

the emotional state is computed by using the

trained SVR models;

 Emotion Classification - The distance between

the positions of the tested piece of violin

music and the state of each basic emotion in

the emotion space is computed to determine

the emotion category. The estimated states of

the six basic emotions (i.e., happiness,

sadness, disgust, comfort, surprise, and

anxiety) are obtained by a questionnaire

survey as well.

Dataset of

Violin Music

Training

Testing

Feature

Extraction

Questionnaire

Survey

Support Vector

Regression

Affinity

Regression

Pleasure

Regression

Arousal

Regression

Emotion

Classification

Affinity

Pleasure Arousal

Figure 7: Framework of emotion recognition of violin

music.

3.3.2 Support Vector Regression

Support Vector Regression is a powerful technique

for regression based on Support Vector Machine

(SVM) (Smola and Schölkopf, 2004), which shows

outstanding performance in emotion recognition of

speech (Grimm, Kroschel, and Narayanan, 2007)

and music (Han et al., 2009) for quantitative analysis.

Suppose the training instances are described as

follows,

{

}

(,),,(, )

yy ℜ⊂ℜ ×vvL ,

(3)

where k is the number of training instances. The goal

is to find a function

()i

which maps the n features

of violin music

= ( , ..., )

T n

vv∈ℜv to the value of

emotional state

y ∈ℜ,

() ()

()

i i

y f= v

(4)

Three SVR functions are created to estimate the

values in the three axes of emotion space, i.e.,

{, , }i Affinity Pleasure Arousal∈ .

The linear function f is described as follows,

() , , ,

fbb= + ∈ℜ ∈ℜvwv w

(5)

where w and b are the parameters of the hyperplane

and

denotes the inner product.

The problem can be formulated as

minimize

subject to

⎧

−−≤

⎪

⎨

+− ≤

⎪

⎩

(6)

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

where

≥ denotes the maximum deviation

between the actual and predictive target.

In order to eliminate the influence of noise and

abnormal samples, the slack variables

and

and a soft margin parameter C are introduced, which

yields the following problem,

minimize ( )

ξξ

∑

subject to ,

, 0

mm m

mmm

ξξ

⎧

−−≤+

⎪

+− ≤+

⎨

⎪

≥

⎩

(7)

The key idea to solve the optimization problem

of Eq. (7) is to construct a Lagrange function, and

then the above problem can be turned into a dual

optimization problem. Finally, the regression

function of

()f v is given as follow,

() ( ) ,

mm m

αα

=− +

∑

vvv

(8)

where

are Lagrange multipliers, and

0 ,

αα

≤ ≤

αα

−≥

. ,

K vv is the

kernel function, where the Gaussian RBF kernel

function is adopted to train the emotion model of

violin music in Affinity-Pleasure-Arousal emotion

space,

( , ) exp( )

−

=−

(9)

4 EXPERIMENTS ON EMOTION

RECOGNITION OF VIOLIN

MUSIC

4.1 Dataset of Violin Music

4.1.1 Emotion Category of Violin Music

There are mainly two kinds of methods for

analyzing music emotion, namely, quantitative

analysis and qualitative analysis, where the

qualitative analysis can obtain the specific category

of the music emotion.

Violin music emotion is actually the human

emotion that is aroused or inspired by the violin

music. Accordingly, different people will have their

own emotion understanding of the same piece of

melody, which means the evaluation of violin music

emotion is somewhat subjective. In addition, it is

difficult to perform detailed classification of music

by nonprofessional people except musicians.

Among the acknowledged emotion categories,

six basic emotions (Oatley and Johnson-Laird, 1987)

including happiness, sadness, disgust, comfort,

surprise, and anxiety are chosen for expressing the

emotion of violin music.

To determine the coordinate of each emotion in

the Affinity-Pleasure-Arousal emotion space, forty

people from seven countries, aged 20 to 30 years,

have participated in questionnaire survey with

eighteen questions - How “Affinity”/“Pleasure”/

“Arousal” do you feel about each basic emotion?

Seven answer options are given for each question,

for example, to describe the “Pleasure”, seven items

that can be expediently chosen by the respondents

are 1-Extremely Displeasure, 2-Very Displeasure, 3-

Displeasure, 4-Medium, 5-Pleasure, 6-Very Pleasure,

and 7-Extremely Pleasure. Each item is assigned

with value for statistical analysis, i.e., 1 (-1), 2 (-

0.66), 3 (-0.33), 4 (0), 5 (0.33), 6 (0.66), and 7 (1).

The average coordinates from questionnaire survey

are Happiness (0.58, 0.63, 0.54), Sadness (-0.47, -

0.44, -0.33), Disgust (-0.34, -0.59, 0.27), Comfort

(0.42, 0.17, -0.61), Surprise (0.27, 0.49, 0.58), and

Anxiety (-0.14, -0.25, -0.18).

4.1.2 Violin Music Data Record

Violin music is performed by an author who has 25

years experience in playing violin, and it is recorded

in a dataset which consists of 60 pieces of famous

violin music selected from concerto, sonata,

symphony, and sound tracks of movies and games,

as enumerated in Table 6.

In general, a piece of violin music lasts minutes

or tens of minutes. For the experiment, each piece is

divided into shorter pieces, where each one lasts 15

seconds. Different movements in the same violin

music may differ in melody and tempo, thus,

emotionally touched clips of violin music are

selected. Using these settings, 120 pieces of violin

music in total are collected to form the dataset of the

experiment. In this dataset, 60 pieces of the violin

music are used for training, and other 60 pieces are

for testing.

All the pieces of violin music in the dataset are

recorded in a unified format. The A440 is adopted as

the standard pitch; the standard tempo (Andante) of

quarter note is set to 72 BPM. The sound tracks are

recorded in 44100Hz, 16bit, and mono, and saved in

WAV format.

EmotionRecognitionofViolinMusicbasedonStringsMusicTheoryforMascotRobotSystem

Table 6: Samples of violin music with six emotions.

Emotion Violin Music Piece Composer

Happiness

Concerto No. 1 in E major, Op. 8,

"La primavera" (Spring) 1st

movement

Antonio

Vivaldi

Violin Concerto No. 4 in D major

Wolfgang

Amadeus

Mozart

The Symphony No. 9 in D minor,

4th movement "Ode to Joy"

Ludwig van

Beethoven

Sadness

Schindler's List John Williams

Castle in the Sky

Joe Hisaishi

Zigeunerweisen (Gypsy Airs),

Op. 20

Pablo de

Sarasate

Disgust

Caprice No. 2

Caprice No. 7

rice No. 13

Niccolò

Paganini

Comfort

Canon in D

Johann

Pachelbel

Swan Lake

Pyotr Ilyich

Tchaikovsky

On Wings of Song

Jakob Ludwig

Felix

Mendelssohn

Bartholdy

Surprise

The Symphony No. 94 in G

major 2nd movement

Franz Joseph

Haydn

Can-can

Jacques

Offenbac

Concerto No. 2 in G minor, Op.

8, "L'estate" (Summer) 2nd

movemen

Antonio

Vivaldi

Anxiety

The Symphony No. 40 in G

minor 1st movement

Wolfgang

Amadeus

Mozar

The Butterfly Lovers

Chen Gang

and He

Zhanhao

Serenade Melancolique, Op. 26

Pyotr Ilyich

Tchaikovsky

4.2 Experimental Results

Experimental results of the proposal are summarized

in Table 7. The “Original” shows the number of

pieces of violin music that are assigned to six emotion

categories, which is determined by questionnaire

survey; the “Detected” is the number of accurate

recognition results of the proposal; the “False”

represents the number of wrong recognition results;

the “Precision” is the ratio of “Detected” to

“Original”. The overall recognition rate achieved is

around 87%.

To give a more detailed explanation of the

experimental results. The six basic emotions are

further categorized into three levels, i.e., “Positive”,

“Neutral”, and “Negative”. Happiness and comfort

belong to the “Positive” level; disgust and surprise

pertain to the “Neutral” level; sadness and anxiety are

assigned to “Negative” level. According to the

experiment results, there are two points that can be

concluded.

Firstly, recognition rates of positive “Happiness”

and positive “Comfort” are better than those of

negative “Sadness” and negative “Anxiety”. The

possible reason could be, on the one hand, the

commonality of positive feelings is higher than that

of the negative feelings in general. On the other

hand, famous (i.e., familiar to auditory) violin music

with sad expression is so frequently performed that

the impression of sadness is somewhat suppressed.

As a result, the recognition rate of negative

emotional states is not prominent due to the influence

of strong subjectivity. It is also noted that, even in the

same level, the recognition rates of “Happiness” and

“Sadness” are slightly higher than those of “Anxiety”

and “Comfort”.

Secondly, as seen in the Table 7, the “Surprise”

receives the highest accuracy while the “Disgust”

receives the lowest, and both of them belong to the

level of neutral. The previous study has drawn a

conclusion that the “neutral” is the most difficult

emotional state to be recognized (Lee, 2011). The

reason for the highest and the lowest could be that the

number of music data for them is less than the others.

Accordingly, when a false or missing result is yielded,

it will significantly impact on the recognition rate.

Table 7: Recognition results of violin music emotion.

Index Emotion Original Detected False Precision

1 Happiness 16 15 1 93.75%

2 Sadness 15 13 2 86.67%

3 Disgust 6 4 2 66.67%

4 Comfort 11 10 1 90.91%

5 Surprise 3 3 0 100%

6 Anxiety 9 7 2 77.78%

Total 60 52 8 86.67%

4.3 Application to Background Music

Selection for Home Party Scenarios

As a universal language of humanity, the music as

well as spoken language is indispensible to achieve

casual communication in human-human interaction

or even human-robot interaction.

In a home party demonstration, communication

between four humans and five eye robots using

Mascot Robot System is performed, where there are

six scenarios, i.e., Scenario 1: “Greeting guests at

the door”, Scenario 2: “Drinking at the mini-bar”,

Scenario 3: “Playing dart game”, Scenario 4:

“Watching TV”, Scenario 5: “Checking timetable of

train at the terminal computer”, and Scenario 6:

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

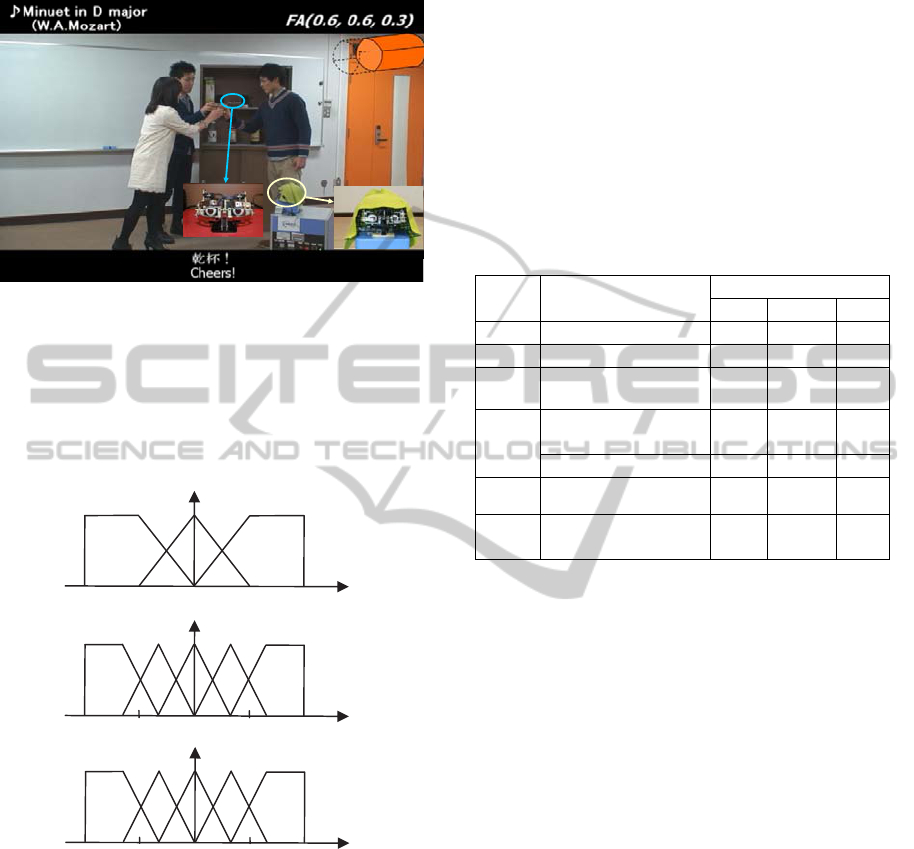
“Farewell to guests at the door”. Fig. 8 shows a

screenshot of Scenario 2.

Figure 8: A screenshot of Scenario 2.

The Fuzzy Atmosfield (Liu et al., 2011) in each

scenario is obtained by integrating all the emotional

states of participants, namely, humans, robots, and

background music. The state of the FA together with

its graphical representation is illustrated at the top

right corner in Fig. 8.

NT P

affinity

-1

0 1

pleasure

arousal

-1

0 1

0.5

-0.5

NT HA

-1

0 1

0.5

-0.5

NT HP

Figure 9: Membership functions for emotion space axes.

Based on the proposed emotion recognition of

violin music, violin music emotion is specified in the

Affinity-Pleasure-Arousal emotion space. To be

convenient to calculate the FA and select appropriate

background violin music, fuzzy logic is used to

further represent the emotion of violin music. The

fuzzy membership functions for the emotion space are

shown in Fig. 9, where the fuzzy domain of each axis

is defined as [-1, 1], and three linguistic variables are

employed for the “Affinity”, i.e., Positive (P), Neutral

(NT), and Negative (N); five linguistic variables for

“Pleasure-Displeasure”, i.e., High Pleasure (HP), Low

Pleasure (LP), Neutral (NT), Low Displeasure (LD),

and High Displeasure (HD); and for “Arousal-Sleep”,

the linguistic variables are High Arousal (HA), Low

Arousal (LA), Neutral (NT), Low Sleep (LS), and

High Sleep (HS).

For each scenario, the target state of the FA is

predefined beforehand. To achieve it, proper violin

music is selected using fuzzy inference, which

contains the music emotion that enables the

atmosphere change toward the target. The specific

violin music chosen for each scenario in the home

party is shown in Table 8.

Table 8: Violin music for six scenarios of home party.

Scenario Violin Music Piece

Emotion

Affinity Pleasure Arousal

1 Canon in D NT

LD NT

2 Minuet in D major P

LP LA

Humoresque, Op.101

No.7

LP LS

Flight of the

Bumblebee

LD HS

Turkish March

HP HA

String Serenade

o.18

in G ma

or 4th

LP LA

Salut D’Amour, Op.

NT LD LS

5 CONCLUSIONS

Emotion recognition of violin music based on the

strings music theory is proposed. According to the

music theory of “Just Intonation”, “Metronome”,

and “Dynamics”, three sets of features of violin

music (i.e., harmony, rhythm, and dynamics) are

adopted to calculate the values of each axis in the

Affinity-Pleasure-Arousal emotion space.

To confirm the validity of the proposed features,

120 pieces of violin music are recorded in a dataset,

in which the music emotions are represented by

happiness, sadness, comfort, disgust, anxiety, and

surprise. Support Vector Regression is used for

training the emotion model of violin music with 60

pieces music. The other 60 pieces are used for

testing, where the proposal achieves 86.67% average

accuracy. The results of “Happiness” and “Comfort”

are better than the others since they belong to

positive feelings, while the two negative feelings

(i.e., “Sadness” and “Anxiety”) receive about 83%

accuracy. The most difficult-to-perceive neutral

feelings, i.e., “Surprise” and “Disgust” obtain the

highest and the lowest accuracy, respectively.

Another three features in Table 5, i.e., Articula-

EmotionRecognitionofViolinMusicbasedonStringsMusicTheoryforMascotRobotSystem

tion, Register, and Timbre, could be used for

emotion recognition of violin music in future work.

And the proposal could be extended to the emotion

recognition of other string instruments such as cello.

Besides the classical music, other types of music

can be performed by violin, e.g., folk music, pop

music, drawing the violin out of classical shell.

Not limited to the home environment, the

proposal could be applied to emotion analysis of

background music on other occasions such as café,

restaurants, supermarket, bar, and geracomium etc.,

where an automatic background music recommenda-

tion system will be further developed to improve the

individual emotion in one-to-one communication or

the atmosphere in many-to-many communication.

What’s more, it can also be used for medical

research such as psychotherapy, where the emotional

music is expected to help people eliminate the stress

or conquer the other psychological diseases.

ACKNOWLEDGEMENTS

This work was supported by Japan Society for the

Promotion of Science (JSPS) under grant

KAKENHI 21300080.

REFERENCES

Ayadi M. E., Kamel M. S., and Karray F., 2011. Survey

on speech emotion recognition: features, classification

schemes, and databases. Pattern Recognition. 44 (3):

572-587.

Barbour J. M., 2004. Tuning and Temperament: A

Historical Survey, Courier Dover Publications. New

York, Dover edition.

Boersma P. and Weenink D., 2008. Praat: doing phonetics

by computer. http://www.praat.org/.

Brown C., 1999. Classical and Romantic Performing

Practice 1750-1900, Oxford University Press.

Cabrera D., 1999. PSYSOUND: A computer program for

psychoacoustical analysis. Proceedings of the

Australian Acoustical Society Conference.

Grimm, M., Kroschel, K., and Narayanan S., 2007.

Support vector regression for automatic recognition of

spontaneous emotions in speech. IEEE Int. Conf. on

Acoustics, Speech and Signal Processing.

Han B.-J., Rho S., Dannenberg R. B., and Hwang E., 2009.

SMERS: music emotion recognition using Support

Vector Regression. 10th International Conference on

Music Information Retrieval.

Hargreaves D. J., 1999. The functions of music in

everyday life: redefining the social in music

psychology. Psychology of Music. 27 (1): 71-83.

Hirota K. and Dong F.-Y., 2008. Development of Mascot

Robot System in NEDO project. In Proc. 4th IEEE Int.

Conf. Intelligent Systems.

Juslin P. N., 2000. Cue utilization in communication of

emotion in music performance: relating performance

to perception. Journal of Experimental Psychology:

Human Perception of Performance. 26 (6): 1797-1813.

Kim Y. E., Schmidt E. M., Migneco R., Morton B. G.,

Richardson P., Scott J., Speck J. A., and Turnbull D.,

2010. Music emotion recognition: a state of the art

review. 11th International Society for Music

Information Retrieval Conference.

Lartillot O. and Toiviainen P., 2007. A Matlab toolbox for

musical feature extraction from audio. 10th Int.

Conference on Digital Audio Effects.

Lee C.-C., Mower E., Busso C., Lee S., and Narayanan S.,

2011. Emotion recognition using a hierarchical binary

decision tree approach. Speech Communication. 53 (9-

10): 1162-1171.

Liu Z.-T., Wu M., Li D.-Y., Dong F.-Y., Yamakaki Y.,

and Hirota K., 2011. Emotional states based 3-D

Fuzzy Atmosfield for casual communication between

humans and robots. In Proc. IEEE Int. Conf. Fuzzy

Systems.

Lu L., Liu D., and Zhang H.-J., 2006. Automatic mood

detection and tracking of music audio signals. IEEE

Transactions on Audio, Speech, and Language

Processing. 14 (1): 5-18.

Nakamura T., 1987. The communication of dynamics

between musicians and listeners through musical

performance. Perception & Psychophysics. 41 (6):

525-533.

Oatley K., Johnson-Laird P.N., 1987. Towards a cognitive

theory of emotions. Cognition & Emotion. 1: 29-50.

Sethares W. A., 1993. Local consonance and the

relationship between timbre and scale. Journal of the

Acoustical Society of America. 94 (3): 1218-1228.

Starks E., 2012. Popular instruments used in classical

music. http://www.ehow.com/about_5377304_popular

-instruments-used-classical-music.html.

Smola A. J. and Schölkopf B., 2004. A tutorial on Support

Vector Regression. Statistics and Computing. 14 (3):

199-222.

Yamazaki Y., Hatakeyama Y., Dong F. Y., and Hirota K.,

2008. Fuzzy inference based mentality expression for

eye robot in Affinity Pleasure-Arousal space. Jounal

of Advanced Computational Intelligence and

Intelligent Informatics. 12 (3): 304-313.

Yamazaki Y., Vu H. A., Le P. Q., Liu Z.-T., Fatichah C.,

Dai M., Oikawa H., Masano D., Thet O., Tang Y.-K.,

Nagashima N., Tangel M. L., Dong F.-Y., and Hirota

K., 2010. Gesture recognition using combination of

acceleration sensor and images for casual

communication between robots and humans. IEEE

Congress on Evolutionary Computation.

Yang Y.-H., Lin Y.-C., Su Y.-F., and Chen H. H., 2008. A

regression approach to music emotion recognition.

IEEE Transactions on Audio, Speech, and Language

Processing. 16 (2): 448-457.

Zweifel P. F., 2005. The mathematical physics of music.

Journal of Statistical Physics. 121 (5-6): 1097-1104.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics