
Generalized Independent Subqueries Method
Tomasz Marek Kowalski
1
, Radosław Adamus
1
, Jacek Wiślicki
1
and Michał Bleja
2
1
Computer Engineering Department, Technical University of Lodz, Lodz, Poland
2
Faculty of Mathematics and Computer Science, University of Lodz, Lodz, Poland
Keywords: Query Optimization, Independent Subqueries, Object-Oriented Database, Stack-Based Approach, SBQL.
Abstract: The following paper presents generalisation of the independent subquery method for object-oriented query
languages. A subquery is considered independent if none of involved names is bound in a stack section
opened by a currently evaluated non-algebraic operator. Optimisation of such a subquery is accomplished
by factoring it out from a loop implied by its query operator. We generalise the method to factor out also
subqueries that are evaluated only in a context of independent subqueries of a given query. The query is
rewritten to an equivalent form ensuring much better performance. Our research bases on the Stack-Based
Architecture of query languages having roots in semantics of programming languages. The paper illustrates
the method on an comprehensive example and finally presents the general rewriting rule.
1 INTRODUCTION
The ODRA system (Lentner and Subieta, 2007) is an
environment facilitating development of object-
oriented data-intensive and distributed applications.
The main component of ODRA is SBQL (Stack-
Based Query Language) (Lentner and Subieta, 2007;
Subieta, 2008 and 2009). SBQL evolved from a pure
database query language to a fully-fledged object-
oriented programming language with a lot of
features such as an UML-like object model,
collections constrained by cardinalities, processing
semi-structured data, static type-checking, closures,
etc. As a query language, SBQL is supported by a
query optimiser, which contains a set of optimisation
methods, including query rewriting (Płodzień,
2000), indices (Kowalski et al., 2008). We have
adapted and generalised some of them from
relational database systems, but in majority they are
totally new. In this paper we propose one of such
new powerful optimisation methods that has not
been presented yet in any source.
Analysing query evaluation in the Stack-Based
Approach (SBA) (Subieta, 2008) one can notice that
some subqueries are processed multiple times in
loops implied by non-algebraic operators, despite the
fact that in subsequent loop cycles their results are
the same. Such subqueries should be evaluated only
once and their result reused in next loop cycles. This
observation is a basis for an important rewriting
optimisation technique called the method of
independent subqueries (Płodzień and Kraken, 2000,
Płodzień, 2000). This method is more general than
classical pushing of a selection/projection known
from relational system and SQL (Ioannidis, 1996).
In SBA it works for any kind of a non-algebraic
query operator and for any object-oriented database
model.
The generalised independent subqueries method
belongs to the group of optimisation methods based
on query rewriting. Rewriting means transforming a
query Q
1
into a semantically equivalent query Q
2
providing much better performance. It is
accomplished according to rewriting rules based on
locating parts of a query matching some pattern.
These parts are to be replaced by other parts
according to these rules. The main benefit from
rewriting is that algorithms are fast, optimisation is
performed before a query is executed and resulting
performance improvement can be very significant,
sometimes several orders of magnitude (concerning
queries’ response times).
Presented method includes cases where an
independent query is divided into two or more parts
(within a larger query), which makes more difficult
to detect and factor out. We show that there is an
efficient rewriting rule to factor an independent
subquery out of a non-algebraic operator together
with its dependent subqueries that are also
independent of this operator. For example, consider
a query – for pairs being a Cartesian product of all
200
Marek Kowalski T., Adamus R., Wi
´
slicki J. and Bleja M..
Generalized Independent Subqueries Method.
DOI: 10.5220/0003994802000204
In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 200-204
ISBN: 978-989-8565-10-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
company employees and departments, taking into
consideration only departments whose bosses earn
more then 2000, return a reference to an Emp object
together with a communicate indicating whether a
salary of the employee is greater than an average
salary calculated for employees working in a given
department:
(Emp as e) join (((Dept where
boss.Emp.sal > 2000) as d).
(e.fullName() + (if (e.sal >
avg(d.employs.Emp.sal)) then “earns”
else “ doesn’t earn “) + “ more than
an average salary of “ + d.name + “
department.”)) (1)
In this case the subquery (Dept where
boss.Emp.sal > 2000) as d) is independent from the
join operator hence it will be factored out of this
operator by the method of independent subqueries.
In the result of transformation performed by this
method we obtain the following query:
(((Dept where boss.Emp.sal > 2000)
as d) groupas aux1).(Emp as e) join
(aux1. (e.fullName() + (if (e.sal >
avg(d.employs.Emp.sal)) then “earns”
else “ doesn’t earn“) + “ more than
an average salary of “ + d.name + “
department.”)) (2)
Unfortunately, form (2) terminates the
optimisation action – no further optimisation by
means of the independent subqueries method is
possible any more. This method cannot factor the
subquery avg(d.employs.Emp.sal) out of the join
operator, despite none of its names (d, employs,
Emp, sal) being bound in the stack section opened
by this operator. The reason is that this subquery is
not independent of its parent non-algebraic operator
(the dot operator after second aux1). However, it is
possible to factor out also the subquery
avg(d.employs.Emp.sal) in (1), because it depends
only on the independent subquery ((Dept where
boss.Emp.sal > 2000) as d). Such a transformation
will result in limiting the number of its evaluations.
This paper explains how such cases can be generally
formalised and what a corresponding rewriting
algorithm should be.
The rest of the paper is organised as follows.
Section 2 describes the overall idea of the
generalised independent subqueries method. Section
3 presents the results of simple experiments with the
method. Section 4 presents conclusions.
2 THE GENERALIZED METHOD
To present SBA and SBQL in the following
examples, we use an object store realising a class
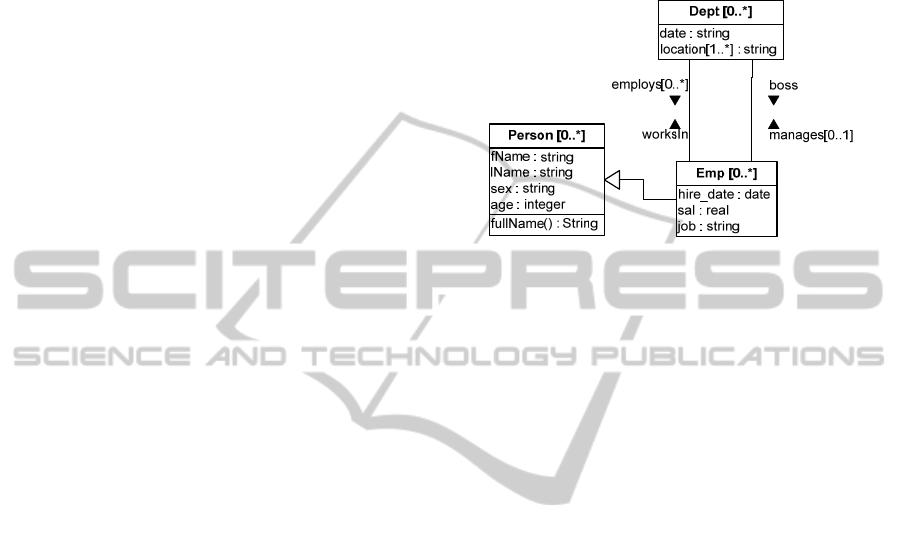
diagram (schema) presented in Fig.1. It defines three
collections of objects: Person, Emp, and Dept.
Person is the superclass of the classes Emp. Names
of classes (attributes, links, etc.) are followed by
cardinality numbers (cardinality [1..1] is dropped).
Figure 1: A schema of an example database.
2.1 The General Idea of the
Optimisation Method
The starting point for the optimisation process is the
method of independent subqueries. If this method
detects an independent subquery like the following
subquery of (1):
((Dept where boss.Emp.sal > 2000) as
d) (3)
that is a left-hand subquery of some non-algebraic
operator then we must analyse the right-hand
subquery of this operator. The subquery ((Dept
where boss.Emp.sal > 2000) as d) in (1) is
connected by the first dot operator with the subquery
(4):
(e.fullName() + (if (e.sal >
avg(d.employs.Emp.sal)) then “earns”
else “ doesn’t earn “) + “ more than
an average salary of “ + d.name +
“department.”) (4)
Because all the names occurring in
avg(d.employs.Emp.sal) are bound in the stack
section opened either by first dot (name d) or in
sections opened by non-algebraic operators of this
query (the other names), this query is dependent
only of the subquery (3). The subquery (3) and
avg(d.employs.Emp.sal) are parts of the right-hand
subquery of the join operator. Since the subquery
avg(d.employs.Emp.sal) is also independent of this
operator so it can be factored out of this operator
together with the independent subquery (3). To
achieve it we construct a query involving the
subqueries like (3) and avg(d.employs.Emp.sal)
connected by the join operator and factor them out
GeneralizedIndependentSubqueriesMethod
201

of the join operator. Moreover, it concerns also the
subquery: “ more than an average salary of “ +
d.name + “ department.”.
Our algorithm operates on the query (2)
transformed by the factoring independent subqueries
method and rewrites it to the following optimised
form:
(((((Dept where manager.Emp.salary >
2000) as d) as aux1_c) join
(aux1_c.(avg(d.employs.Emp.sal)
groupas aux1_1, (“ more than an
average salary of “ + d.name + “
department.”) groupas aux1_2)))
groupas aux1).((Emp as e) join
(aux1.(aux1_c.((e.fullName() + (if
(e.sal > aux1_1) then “ earns” else
“ doesn’t earn“) + aux1_2))))) (5)
Unique names aux1_c, aux_1_1, aux1_2 are
automatically assigned by the optimiser. In the first
three lines of (5), before the last dot, the query
returns a bag named aux1 consisting of structures.
Each structure has three fields:
• aux1_c – with a binder d holding a reference
to a Dept object,
• aux1_1 – the average salary calculated for
employees of the given department,
• aux1_2 – the string “more than ….
department” with the name corresponding to
the given department.
The last dot in the third line puts on top of ENVS
a binder aux1 containing those structures. It is then
used to calculate the query in the following lines. In
this way, average salaries are calculated for each
department once and they are used in the final query,
as required.
Detecting subqueries like
avg(d.employs.Emp.sal) is accomplished by
analysing in which section of the environment stack
the names occurring in a subquery are to be bound.
The binding levels for names are compared to the
scope numbers of non-algebraic operators.
2.2 The General Rewriting Rule
Let us consider the query in the form (6) (denotes
string concatenation and α
i
denotes a part of an
arbitrary query):
α
0
° Q1 groupas N ° α1 ° N ° α2 (6)
Such a query pattern is a result of applying the
independent sub-query method. The Q1 sub-query
represents the part that was factored out and grouped
under the name N. Referring to name N in the
further part of the query (shown in (6)) represents
the use of the result. Obviously to enable binding
name N, the α1 query part must assure the
appropriate ENVS state, but from the perspective of
our method this is irrelevant because of the
compilation error that appears otherwise.
It is worth noticing that the (6) form can be also
a result of some other query transformation or a
direct query writing.
Let us now consider the situation where (6) has
the form (7):
α0 ° Q1 groupas N ° α1 °
(N Θ1 (αz0 ° z1 ° αz1° z2 ° … ° α
zn-1
° z
n
° α
zn
)) ° α
3
(7)
The query (7) contains Θ
1
– a non-algebraic
operator whose left hand operand is a single name
query and the right-hand operand includes
subqueries z
i
(iϵ1..n). The characteristics of z
i
subqueries is that they depend only on an
environment introduced by the Θ
1
operator and some
global (from the point of view of the evaluation of
(6) query) environment. In other words they are
independent of any non-algebraic operators that
appear in the α
1
query part.
The query string (7) represents the general state that
is a starting point for our rewrite algorithm that can
be described as follows.
The z
i
subqueries are factored out from the Θ
1
operator (and any other that appear in α
1
) and joined
with Q
1
query (with the use of non-algebraic
operator join).
((Q
1
as N_C) join (N_C.(z
1
groupas
N_1, z
2
groupas N_2, …, z
n
groupas
N_n))) groupas N (8)
The Q
1
query results are named N_C with use of
as operator instead of groupas because each of the
Q
1
result should be processed separately by the join
operator and should become a context for the
subsequent z
i
queries evaluation. The use of join
operator as well as naming the Q
1
result and
subsequent z
i
results (N_i, I ϵ 1..n) preserves all the
partial results (for further use) in the form of a bag
of structures named N. In the query (7) the z
i
subqueries are replaced with name queries that refers
to names N_i. The query is additionally modified
with introducing another dot operator that creates an
environment containing binders with N_C and N_i.
The modified query takes the form (9):
α
0
° (((Q
1
as N_C) join
(N_C.(z
1
groupas N_1, z
2
groupas N_2,
…, z
n
groupas N_n))) groupas N) ° α
1
° (N.(N_C Θ
1
(α
z0
° N_1 ° α
z1
° N_2 °
… ° α
zn-1
° N_n ° α
zn
))) ° α
3
(9)
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
202
This is the final result of the main algorithm process.
Notice that the result query contains similar patterns
to the one that appear in the initial state (6). Each
pair of the subqueries: z
i
groupas N_i and α
zi-1
° N_i
° α
zi
are similar to the structure of the (6).
Consequently (9) can be represented as follows:
α
0
’
° z
i
groupas N_i ° α
1
’
° N_i ° α
2
’
(10)
If the (10) has the form corresponding to (7):
α
0
’
° z
i
groupas N_i ° α
1
’
° (N_i Θ
1
’
(α
z0
’
° z
1
’
° α
z1
’
° z
2
’
° … ° α
zn-1
’
° z
n
’
° α
zn
’
)) ° α
3
’
(11)
then the optimisation can be recursively applied to
the query.
All the described transformations are, in reality,
performed on an abstract syntax tree (AST) query
representation. The description use string
representation due to conciseness.
3 OPTIMISATION GAIN
The method has been experimentally tested within
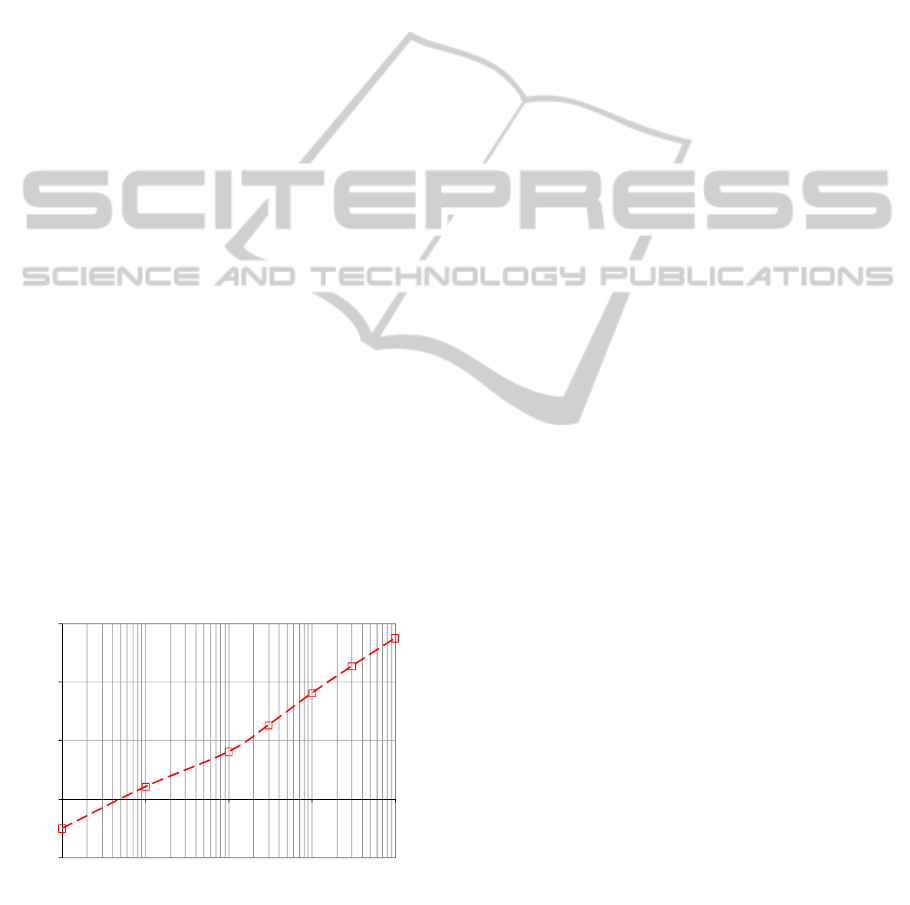
the ODRA system. Fig.2 presents the performance
gain after optimisation of query (1) according to the
Generalised independent subqueries method, i.e. to
the form (5). For instance, on a collection of 10000
employee objects, execution of the optimised one is
approximately 64 times faster. In contrast, our tests
have shown that the standard factoring out method
applied to the query (1) (i.e., transforming it to the
form (2)) does not introduce optimisation gain
greater than 2 in all tested cases. The advantage of
the proposed method is being able to correctly factor
out the most expensive part of the query (1), i.e.
avg(d.employs.Emp.sal)
Figure 2: Optimization gain between evaluations of query
(1) and (10).
According to the expectations, correct factoring
out of a complex subquery results in improving of a
query performance by orders of magnitude.
4 CONCLUSIONS
The presented generalised version of the
independent subquery method is an effective
complement to the original method. Applied
repeatedly (after factoring), it detects and resolves
subsequent independent subqueries in a query. Our
rewriting rule is general, it works for any non-
algebraic operator and for any data model (assuming
that its semantics would be expressed in terms of
SBA). The rule makes also no assumptions
concerning what type an independent subquery
returns: it may return a reference to an object, a
single value, a structure, a collection of references, a
collection of values, a collection of structures, etc.
Finally the rule enables rewriting for arbitrarily
complex nested subqueries, regardless of their left
and right contexts.
Nevertheless, preliminary studies show
possibilities of designing methods based on
factoring out in cases that are still not covered, e.g.
when the left-hand operand of operator Θ
1
in the
query (7) is a complex subquery containing name N.
ACKNOWLEDGEMENTS
This research work is funded from the Polish
Ministry of Science and Higher Education finances
in years 2010-2012 as a research project nr N N516
423438.
REFERENCES
Cluet, S., Delobel, C., 1992, A General Framework for the
Optimization of Object-Oriented Queries. Proc.
SIGMOD Conf., 383-392
Ioannidis Y. E., 1996 Query Optimization. Computing
Surveys, 28(1), 121-123
Kowalski, T., et al., 2008, Optimization by Indices in
ODRA. Proc. 1st ICOODB Conf., 97-117
Lentner, M., Subieta, K., 2007, ODRA: A Next
Generation Object-Oriented Environment for Rapid
Database Application Development. Proc. 11th ADBIS
Conf., Springer LNCS 4690, 130-140
Płodzień, J., Kraken, A., 2000, Object Query Optimization
through Detecting Independent Subqueries.
Information Systems 25(8), 467-490
Płodzień, J., 2000, Optimization Methods in Object Query
Languages. Ph.D. Thesis. Institute of Computer
Science, Polish Academy of Sciences, http://www.
0,1
1
10
100
1000
10 100 1000 10000 100000
optimization gain [ratio]
no. of em
p
lo
y
ees
GeneralizedIndependentSubqueriesMethod
203

sbql.pl/phds/PhD Jacek Plodzien.pdf
Subieta, K., 2008, Stack-Based Approach (SBA) and
Stack-Based Query Language (SBQL). http://www.
sbql.pl
Subieta, K., 2009, Stack-based Query Language.
Encyclopedia of Database Systems 2009. Springer US,
2771-2772
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
204
