An Efficient Sampling Scheme for Approximate Processing of

Decision Support Queries

Amit Rudra

, Raj P. Gopalan

and N. R. Achuthan

School of Information Systems, Curtin University, Kent Street, Bentley, WA 6155, Australia

Department of Computing, Curtin University, Kent Street, Bentley, WA 6155, Australia

Department of Mathematics and Statistics, Curtin University, Kent Street, Bentley, WA 6155, Australia

Keywords: Sampling, Approximate Query Processing, Data Warehousing.

Abstract: Decision support queries usually involve accessing enormous amount of data requiring significant retrieval

time. Faster retrieval of query results can often save precious time for the decision maker. Pre-computation

of materialised views and sampling are two ways of achieving significant speed up. However, drawing

random samples for queries on range restricted attributes has two problems: small random samples may

miss relevant records and drawing larger samples from disk can be inefficient due to the large number of

disk accesses required. In this paper, we propose an efficient indexing scheme for quickly drawing relevant

samples for data warehouse queries as well as propose the concepts of database and sample relevancy ratios.

We describe a method for estimating query results for range restricted queries using this index and

experimentally evaluate the scheme using a relatively large real dataset. Further, we compute the confidence

intervals for the estimates to investigate whether the results can be guaranteed to be within the desired level

of confidence. Our experiments on data from a retail data warehouse show promising results. We also report

the levels of accuracy achieved for various types of aggregate queries and relate them to the database

relevancy ratios of the queries.

1 INTRODUCTION

Analytical queries containing aggregate functions

such as sum and average on a data warehouse are

used to gain a good sense of the business situation

and to support business decisions. Most often we

require timely retrieval of query results with an

acceptable level of accuracy rather than absolute

precision, and so approximate results within certain

limits of accuracy will be acceptable to the user. Pre-

computation with materialized views and sampling

are two ways to handle such queries. However, it is

impractical to maintain a large number of

materialized views for all possible combinations of

information retrieval (Hellerstein et al., 1997). In

contrast, sampling can provide faster results that are

accurate within given assured confidence levels.

The main motivation for use of sampling in

processing queries on a large database or a data

warehouse is to save time and resources. Even

though random sampling is both efficient and

effective as an approximation method, its use for

database querying has attracted significant research

interest only recently (Li et al, 2008); (Joshi and

Jermaine, 2008); (Jin et al., 2006). Sampling has

also been shown to be effective for aggregate

queries (Hellerstein et al., 1997); (Jermaine, 2007;

(Jin et al., 2006); (Jermaine, 2003); (Bernadino et

al., 2002); (Speigel and Polyzotis, 2009; Jermaine et

al., 2004). As sampling data may not be fully

representative of the entire data in a data warehouse,

it is desirable to return both the query result and the

confidence intervals that indicate the reliability of

the results (Li et al, 2008).

A significant problem with random sampling for

database queries from a database on stored disk is

that picking records at random requires almost the

same amount of I/O as processing the query over the

whole database (Olken and Rotem, 1990). To keep

down the cost of sampling based query processing, a

more efficient method of drawing samples is needed.

Another problem is that a random sample drawn

from a very large dataset may not contain relevant

records that satisfy the range restrictions of a given

query. To deal with this problem, we require a

sampling scheme that will include in the sample

Rudra A., Gopalan R. and Achuthan N..

An Efﬁcient Sampling Scheme for Approximate Processing of Decision Support Queries.

DOI: 10.5220/0003995100160026

In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 16-26

ISBN: 978-989-8565-10-5

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

records satisfying the query predicates.

Joshi and Jermaine (2008) introduced the ACE

Tree which is a binary tree index structure for

efficiently drawing samples for processing database

queries. They demonstrated the effectiveness of this

structure for single and two attribute database

queries, but did not deal with multi-attribute

aggregate queries. For extending the ACE Tree to k

key attributes, Joshi and Jermaine proposed binary

splitting of one attribute range after another at

consecutive levels of the binary tree starting from

the root; from level k+1, the process is repeated with

each attribute in the same sequence as before. This

process could lead to an index tree of very large

height for a data warehouse even if only a relatively

small number of attributes are considered.

Li et al. (2008) proposed a sampling cube

framework for answering analytical queries on a

data warehouse which calculates confidence

intervals for any multidimensional query. The

sampling cube is constructed from a random sample

of the data warehouse. After building the sampling

cube, there is no further access to the original data

records should a query require a different sample

from the one already drawn. If a query has too few

sample records in the sampling cube, they expand

the query to gather more sample records from the

sampling cube itself in an attempt to improve the

quality of the query result.

In this paper, we propose the k-MDI Tree which

extends the ACE Tree structure to deal with multi-

dimensional data warehouse queries. Unlike the

ACE Tree, the k-MDI tree allows non-binary splits

of data ranges for key values that do not split evenly

into 2

distinct ranges. The number of levels in the k-

MDI tree can be limited to the number of key

attributes. The shallow tree structure resulting from

multi-way branching also facilitates quicker retrieval

of leaf nodes from disk storage. Unlike the sampling

cube of Li et al. (2008), new samples that contain

relevant records are drawn for each query. These

records can be considered as drawn from a subset of

the data warehouse that satisfies the query

predicates. In estimating the query results, we take

into account the proportion of relevant records for

the query in the whole data warehouse. The

sampling and estimation methods are evaluated

experimentally using a real life data set.

The rest of the paper is organized as follows: In

Section 2, we define some relevant terms and briefly

describe the ACE Tree structure. In Section 3, our k-

way multi-dimensional (k-MDI) indexing structure

is described in detail. We also introduce the concept

of relevancy ratios, both for the database and a

specific sample. Section 4 reports the experimental

results that evaluate the efficacy of our scheme.

Section 5 is the conclusion of the paper.

2 TERMS, DEFINITIONS AND

ACE TREE STRUCTURE

In this section, we define some terms pertaining to

data warehousing, define confidence interval and

then review briefly the ACE Tree structure (Joshi

and Jermaine, 2008) that has preceded the k-MDI

tree we propose in Section 3.

2.1 Dimensions and Measure

To support decision support queries, data is usually

structured in large databases called data warehouses.

Typically, data warehouses are relational databases

with a large table in the middle called the fact table

connected to other tables called dimensions. For

example, consider the fact table Sales shown as

Table 1. A dimension table Store linked to StoreNo

in this fact table will contain more information on

each of the stores such as store name, location, state,

and country (Kimball and Moss, 2002). Other

dimension tables could exist for items and date. The

remaining attributes like quantity and amount are

typically, but not necessarily, numerical and are

termed measures. A typical decision support query

aggregates a measure using functions such as Sum(),

Avg() or Count(). The fact table Sales along with all

its dimension tables form a star schema.

Table 1: Fact table Sales.

SALES

Store

Date Item Quantity Amount

21 12-Jan-11 iPad 223 123,455

21 12-Jan-11 PC 20 24,800

24 11-Jan-11 iMac 11 9,990

77 25-Jan-11 PC 10 12,600

In decision support queries a measure is of

interest for calculation of averages, totals and

counts. For example, a sales manager may like to

know the total sales quantity and amount for certain

item(s) in a certain period of time for a particular

store or even all (or some) stores in a region. This

may then allow her to make decisions to order more

or less stocks as appropriate at a point in time.

AnEfficientSamplingSchemeforApproximateProcessingofDecisionSupportQueries

2.2 Confidence Interval

When estimating with samples we indicate the

reliability of the estimate by its confidence interval.

Consider a sample of records x with the mean of the

sample denoted by ̅, and the size of the sample n.

For a desired confidence level (e.g. 95%) the

confidence interval estimator of the population mean

is given by:

̅ – t

α/2





√





, ̅ + t

α/2





√



where t

α/2

 is the critical t-value and s the standard

deviation of the sample (Keller, 2009).

2.3 ACE Tree Structure

The ACE Tree is a balanced binary tree where the

leaf nodes contain the randomized samples of key

values and the internal nodes above them are the

index nodes. Each internal node contains a range R

of key values, a key value k that splits R into left and

right sub-trees, pointers to the left and right branch

(child) nodes, and counts of database records falling

in the left and right sub-trees. Figure 1 shows the

structure of an example ACE Tree. The root node I

1,1

with its range I

1,1

.R labeled as [0-64] signifies the

key value range of the whole data set. The key of the

root node partitions the range I

1,1

.R into I

2,1

.R = [0-

32] and I

2,2

.R = [33-64]. This partitioning of ranges

is propagated down the tree among the descendants

of respective nodes. The ranges associated with a

section of a leaf node are determined by the ranges

associated with each internal node on the path from

the root node to the leaf. If we look at the path from

1,1

i.e. the root node down to the leaf node L

, we

come across the following ranges 0-64, 0-32 and 17-

24. A leaf node is partitioned into sections (S

, S

…), their number depending on the number of

dimensions indexed. Thus, the first section L

has

a random sample of records in the range 0-64; L

has them in the range 0-32; L

in the range 17-32

and L

in the range 25-32. The size of each leaf is

chosen as the number of records that can be stored in

a disk block and so the number of leaf nodes

depends on the size of the database which also

determines the height of the index tree itself.

2.4 Sampling for a Query using the

ACE Tree

Referring to Figure 1, consider a query Q with a

range of [28-38]. The query execution algorithm

proceeds by traversing down I

1,1

, the root node. Both

2,1

.R and I

2,2

.R overlaps with Q.

Figure 1: Structure of the ACE Tree.

A level down from I

2,1

, only I

3,2

.R, overlaps with

Q. Traversing down to the leaf nodes, the algorithm

finds the right leaf node’s range [25-32] overlaps

with Q and so retrieves records from L

. The

relevant records in the query’s range are returned for

the sample which includes record 28 from L

record 30 from L

and records 29 and 31 from

. Next, the algorithm traverses down the right

node I

2,2

below the root to the leaf node L

and

retrieves all relevant records from all sections of L

to the pool of sample records.

2.5 Extended ACE Tree for Multiple

Dimensions

Joshi and Jermaine (2008) proposed extending the

ACE Tree from a single dimension to multiple

dimensions as follows: Given key attributes

(dimensions), a

, ..., a

, split the range of values for

into two sub trees of approximately equal number

of keys below the root (level 1); for each node at

level 2, similarly perform a binary split of the range

of key values for a

and so on up to level k for

attribute a

. Then at level k+1, split the attribute

values of a

again followed by a

, etc. at further

lower levels.

In real life data, a dimension’s values may not

split evenly into 2

distinct ranges. For example, if a

dimension has an odd number of key values, say -

, k

and k

, with cardinalities of 30000 each; then,

we cannot split them evenly into 2 distinct ranges

but we can do so into 3. The height of the tree will

be very large even for a moderate sized data

warehouse with a relatively small number of

dimensions.

1,1

3,1

3,3

0-32

0-64

33-64

0-16 33-48

17-32

49-64

Index Nodes

(

circled numbers

indicate median,

quartile,… values)

Leaf

Nodes

19 30

0-64 0-32 17-32 25-32

Sections of a lea

node (

with sample

records showing thei

key values)

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

3 MULTIDIMENSIONAL

INDEXING

We propose the k-MDI tree which extends the ACE

Tree index for multiple dimensions while

overcoming the limitations of the ACE Tree

discussed in Section 2.5. The height of the k-MDI

tree is limited to the number of key attributes. As a

multi-way tree index, it is relatively shallow even for

a large number of key value ranges and so requires

only a small number of disk accesses to traverse

from the root to the leaf nodes.

3.1 k-ary Multidimensional Index

(k-MDI)

The k-ary multi-dimensional index tree (k-MDI tree)

is a k-ary balanced tree as described below:

1. The root node of a k-MDI tree corresponds to the

first attribute (dimension) in the index.

2. The root points to k

≤ k) index nodes at level

2, with each node corresponding to one of the k

splits of the ranges for attribute a

3. Each of the nodes at level 2, in turn, points to up

to k

≤ k) index nodes at level 3 corresponding to

splits of the ranges of values of attribute a

;

similarly for nodes at levels 3 to h, corresponding to

attributes a

,..., a

4. At level h, each of up to k

h-1

nodes points to up to

≤ k) leaf nodes that store data records.

5. Each leaf node has h+1 sections; for sections 1 to

h, each section i contains random subset of records

in the key range of the node i in the path from the

root to the level h above the leaf; section h+1

contains a random subset of records with keys in the

specific range for the given leaf.

Thus, the dataset is divided into a maximum of k

leaf nodes with each leaf node, in turn, consisting of

h+1 sections and each section containing a random

subset of records. The total number of leaf nodes

depends on the total number of records in the dataset

and the size of a leaf node (which may be chosen as

equal to the disk block size or another suitable size).

More details on leaf nodes and sections are given in

Section 3.3. In real data sets, the number of range

splits at different nodes of a given level i need not be

the same. For convenience, the number of splits at

all levels are kept as k in Figure 2 that shows the

structure of the general scheme for k-MDI multilevel

index tree of attributes A

, A

, …, A

with k ranges

, R

, …, R

), (R

, R

, …, R

), … (R

, R

, …,

) respectively at levels (1, …,h).

An example of the k-MDI tree is shown in Figure

3 from a store chain dataset with three dimensions –

store, date sold and item number. The number of

range splits and hence branches from non-leaf nodes

vary between 2 and 4 in this example.

3.2 Leaf Nodes

Similar to the ACE tree structure, the lowest level

nodes of a k-MDI tree point to leaf nodes containing

data records. The data records are stored in h+1

sections, where h is the height of the tree. Section S

of every leaf node is drawn from the entire database

with no range restriction on the attribute values.

Each section S

(2 ≤ i ≤ h+1) in a leaf node L is

restricted on the range of key values by the same

restrictions that apply to the corresponding sub-path

along the path from the root to L. Thus for section

, the restrictions are the same as on the branch to

the node at level 2 along the path from the root to L

and so on.

Figure 3 shows an example leaf node projected

from the sample k-MDI tree. The sections are

indicated above the node with attribute ranges for

each section below the node. The circled numbers in

each section indicate record numbers that are

randomly placed in the section. The range

restrictions on the records are indicated below each

section, where the first section S

has records drawn

from the entire range of the database. Thus, it can

contain records uniformly sampled from the whole

dataset. The next section S

has restriction on the

first dimension viz. store (for leaf node L

this range

is store numbers 1-16). The third section S

has

restrictions on both first and second dimensions viz.

store and date. While the last section S

has

restrictions on all the three dimensions – store, date

and item.

The scheme for selection of records into various

leaf nodes and sections is explained in detail in the

following section.

3.3 Building the k-MDI Tree

The purpose of the k-MDI tree is to quickly retrieve

relevant random samples of records for processing

data warehouse queries. The records in the sample

are obtained from leaf nodes by traversing the index

from the root. The k-MDI Tree is built in the

following three steps:

1. First, the dataset records are sorted by the first

key attribute a

as the major field, followed by the

second attribute a

and so on until the last attribute

AnEfficientSamplingSchemeforApproximateProcessingofDecisionSupportQueries

2. The next step is to find the split points of key

attribute values in the index tree at the levels 1 to h

so that the number of records of the dataset that fall

under each sub-tree rooted at levels 2 to h is

approximately equal. The k

-1 split points at level 1

are chosen such that the total number of records in

the dataset are split into k

approximately equal

parts; the records falling under each of the nodes at

level 2 are split into k

approximately equal parts,

and so on until the records falling under each of the

nodes at level h split into k

approximately equal

parts. The number of splits at all the levels in the

index should be such that the number of leaf nodes

are equal to a pre-computed number based on the

total number of records in the dataset and the size of

each leaf node (which could be chosen as the disk

block size as in the case of the ACE Tree or some

other suitable size).

3. Next, a random number between 1 and h+1 is

assigned to each data record as its section number.

Depending on the section number and its composite

key value, the record is assigned to a leaf node as

follows: If the section number is 1, the record is

assigned randomly to any one of the leaf nodes in

the tree; if the section number is i (2≤i≤h), starting

from the root of the index tree, we locate the root of

a sub-tree at level i in which the key of the record

falls and assign the record randomly to section i of

any of the leaf nodes in that sub-tree;

if the record’s section number is h+1, it is assigned

to the specific leaf node where the record’s key

value belongs. When all the records have been thus

assigned section and leaf node numbers, the dataset

is re-organised with records sorted according to their

leaf node and section numbers.

3.4 Using the k-MDI Tree for Data

Warehouse Queries

By using a k-MDI tree index, we can draw stratified

samples for data warehousing queries from restricted

ranges of key values. In this section, we first

introduce two measures that are useful for the

estimation of query results using such samples. The

database relevancy ratio (DRR) of a query Q,

denoted by ρ(Q) is the ratio of the number of records

in a dataset D that satisfies the query conditions to

the total number of records in D. For a query with

no condition, ρ(Q) is 1. Similarly, the sample

relevancy ratio (SRR) of a query Q for a sample set

S, denoted by ρ(Q, S) is defined as the ratio of the

number of records in S that satisfy a given query Q

to the total number of records in S.

In a true random sample of records, the SRR for

a query Q is expected to be equal to its DRR, i.e.,

E(ρ(Q, S) ) = ρ(Q). A sample with ρ(Q, S) > ρ(Q) is

likely to give a better estimate of the mean than a

true random sample. However, for the sum of a

column, the sample needs to be representative of the

population, i.e., ρ(Q, S) should be close to ρ(Q).

Consider the following formula for estimating

the sum (Berenson and Levine, 1992): 



=̂



where N is the cardinality of the population, ̂ the

estimated proportion of records satisfying the query

conditions and 



the mean of records in the sample

satisfying the query condition. In order to estimate

the mean we can use all relevant sampled records

from all sections of the retrieved leaf nodes, but to

estimate the sum we can use sampled records

Figure 2: General structure of the k-MDI tree – A

, A

, …, A

are h attributes and R

the i-th attribute’s j-th range high

water mark (HWM).

. . .

12 . . .

Leaf nodes

. . .

Index tree

... A

h-1

h-1 1

h2 …

... A

22 …

... A

22 …

... A

22 …

... ... .... . .

. . .

... A

h-1

h-1 2

h2 …

. . .

... A

h-1

h-1 k

h2 …

...

... ...

. . .

...

Level 1-Dim A

Level 2-Dim A

Level h-Dim A

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

only from section S

, which is the only section with

records drawn randomly from the entire dataset. For

estimating the sum for a query with conditions on

some of the indexed dimensions we use appropriate

sections of the retrieved leaf nodes to get a better

estimate of the mean; the records from section S

are

also used to get a fair estimation of the proportion

records that satisfy the query conditions.

3.5 Effect of Sectioning on Relevancy

Ratio

As discussed earlier, sections S

to S

h+1

of each leaf

node contain random collections of records with the

difference that S

contains records from the entire

dataset while other sections contain random records

from restricted ranges of the key attributes. Consider

a query with the same range restrictions on all three

dimensions (store, date and item) as section L

Figure 3. We are then likely to get more relevant

records in the sample from the second section L

than from S

since records of S

have restrictions on

the first dimension of store that matches the query

condition. Records in S

will have restrictions on

both store and date dimensions that match that of the

query and so are likely to contain more relevant

records than in S

. All records in section L

will

satisfy the query since the range restrictions on S

exactly match the query. Mathematically, for a query

Q having restrictions as mentioned above:

ρ(Q) = E(ρ(Q, L

)) ≤ E(ρ(Q, L

))

≤ E(ρ(Q, L

)) ≤ E(ρ(Q, L

))

Using this property of the k-MDI tree, it is possible

to quickly increase the size of a sample that is too

small, by including more records from other sections

of the retrieved leaf nodes.

3.6 Record Retrieval to Process a

Query

The objective of using the k-MDI tree is to retrieve a

significant number of relevant records (i.e. records

that satisfy the query conditions) in the sample

drawn for processing a given query. The query

conditions may span sections of one or more leaf

nodes which can be reached from index nodes that

straddle more than one range of attribute values.

These leaf nodes can be accessed by traversing the

tree from the root using the attribute value ranges in

the query conditions and sections from multiple leaf

nodes can be combined to form the sample.

We describe the retrieval process using an

example query on the sample database of Figure 4.

Consider a query Q

about sales in store 12 for date

range 1-13 and item range 12M-20M. The retrieval

algorithm finds the sections of leaf nodes for this

query as follows:

1. Search index level 1 to locate the relevant store

range. Store 12 is in the left most range of 1-16.

2. Traverse down to index level 2 (date), indicated

by a dashed arrow in Figure 4, along the first store

range. Since there is a condition on date (1-13),

compare the HWMs (high water marks) of the three

ranges and find that it fits into two date ranges viz.

the first and the second. Make a note of these date

ranges.

3. Traverse down using the first date range to the

next index level which has item ranges. Since there

is a condition on item numbers (12M-20M),

compare this range with HWMs and find that it fits

into two ranges viz. the third and the fourth. Make a

note of these item ranges.

4. Traverse down using the third item range to

relevant leaf pages and make a note of them.

5. Iterate step 4, except this time using the fourth

item range.

6. Next, repeat the above three steps i.e. steps 3

through 5; but this time using the second date range

instead.

7. Now retrieve records from the relevant sections

in the four leaf nodes (viz. L

, L

and L

) to form

a sample for the given query.

3.7 Estimating Query Results from

Samples

In decision support queries on large databases, the

most common estimation performed is either of the

mean or the sum of a column measure (Jin et al.,

2006). We maintain a table representing a histogram

of record counts for each leaf node and its sections.

It is used to estimate the number the leaf nodes

required to have adequate number of samples. The

following steps outline our method of estimating the

mean, sum, standard deviation and the confidence

intervals:

1. Draw a sample set L of leaf nodes as described in

Section 3.6 for the given sampling rate.

2. The following parameters are computed:

a. Sample size – n

b. Count of sampled records satisfying the

query condition – m

c. Count of records in all sampled S

sections of L

– n′

d. Count of records in all sampled

sections of

AnEfficientSamplingSchemeforApproximateProcessingofDecisionSupportQueries

Figure 3: A leaf node (changes in range values for attributes are indicated in bold).

Figure 4: Navigation down index tree nodes for conditions on three dimensions.

L satisfying the query condition – m′

e. Sum of attribute (variable) value of all m

records – sum

f. Sum of squares of attribute value of the all

abovementioned m′ records – ′

g. The average sum of squares - Z = 





Store# Item#

1 – 60 1 – 31 1M-21M

16 4 1 6 0

Date

Store# Item#

1 – 16 1 1 20 3 1 1

M-21M

Date

1 - 16

1 - 11 12 -20

Store#

Item#

1 – 16 1 – 11

10M 15M 21M

Date

St ore #: 1-60 1-16 1-16 1-16

Dat e: 1 -31 1-31 12-20 12-20

Ite m# : 1 M-21M 1M-21 M 1M-21 M 11M-15M

1M–7M

Level 1 index

(Store)

Level 2 index

(Date)

Level 3 index

(Item)

Leaf nodes

Sections of a leaf node

Attribute ranges

1,1

2,1

3,1

Store# Item#

17 – 4 1 11 20 31 1

M-21M

Date

2,2

Store# Item#

42 – 60 11 20 3 1 1

M-21M

Date

21 - 31

17-41 42 -60

8M–10M 11M–15M16M–21M

Store#

Item#

1 – 16 12 – 20

10M 15M 21M

Date

1M–7M

3,2

8M–10M 11M–15M 16M–21M

. . . . . . . . . . . . . . . . . .

. . . . . . . . .

Store#

Item#

42 – 60 2 1 – 3 1

10M 15M 21M

Date

1M–7M

3,9

8M–10M 11M–15M 16M–21M

21 -31

Store# Item#

1 – 60 1 – 31 1M-21M

16 41 60

Date

Store# Item#

1 – 16 11 20 31 1

M-21M

Date

Store#

Item#

1 – 16 1 – 11

10M 15M 21M

Date

Store#: 1-60 1-16 1-16 1-16 1-60 1-16 1-16 1-16 1-60 1-16 1-16 1-16 1-60 1-16 1-16 1-16

Date: 1-31 1-31 1-11 1-11 1-31 1-31 1-11 1-11 1-31 1-31 12-20 12-20 1-31 1-31 12-20 12-20

Item#:

1M-21M 1M-21M 1M-21M 11M-15M 1M-21M 1M-21M 1M-21M 16M-21M 1M-21M 1M-21M 1M-21M 11M-15M 1M-21M 1M-21M 1M-21M 16M-21M

1,1

2,1

3,1

Store# Item#

17– 41 11 20 31 1M-21M

Date

2,2

Store# Item#

42 – 60 11 20 31 1M-21M

Date

Store#

Item#

1 – 16 12 –20

10M 15M 21M

Date

3,2

. . . . . .

. . .

. . . . . . . . .

. . . . . .

. . .

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

3. Estimating the sum, average, variance and C.I.

limits (Chaudhuri and Mukherjee, 1985):

a. Estimate of the number of records M that

satisfy the query condition in the population

(given the cardinality of the dataset N)





b. Estimate of Average ̅ =

c. Estimate of Sum





=



̅

d. Estimate of variance of Average v(

)

e. Confidence interval lower limit

f. Confidence interval upper limit

4 EXPERIMENTAL RESULTS

To evaluate the effectiveness of our sampling

technique based on the k-MDI tree, we performed

experiments on real life supermarket retail sales data

(TUN, 2011) for a month from 150 outlets. The data

warehouse is structured as a star schema shown in

Figure 5, with the fact table (itemscan) consisting of

over 21 million rows and three dimension tables viz.

storeInfo, itemDesc and storeMemberVisits. TPC-H

queries (TPC Benchmarks, 2011) with suitable

modifications for this sample data warehouse were

used in the experiments. Most of the TPC-H queries

involve SQL aggregate functions of sum(), avg() or

count(). A few include min() and max() which are

not easily calculated by sampling (Joshi, 2008;

Hellerstein et al., 1997). So, we investigated only

sum, avg and count in our experiments. The index

tree structure was simulated using the Oracle

DBMS. We clustered the fact table on leaf and

section number to maintain the records in that

sequence. This organisation supported the

simulation of both the storage and retrieval of

records for the experiments.

A set of three queries were used containing the

SQL functions – avg(), sum(), count() with varying

database relevancy ratios (DRR). The queries were

of the form:

Select Avg(totscanAmt), Sum(totscanAmt),

Count(*)

From itemscan, storeinfo, itemdesc

Where storeno between s1 and s2

And itemscan.storeno=storeinfo.storeno

And itemscan.itemno=itemdesc.itemno

And datesold between d1 and d2

And itemno between i1 and i2;

The DDR value was set high or low for the queries

by choosing a given proportion of the dimension

range for the query. For example, assuming a

uniform distribution of values for a dimension in the

database, we can get a DRR of approximately 0.33

on a single dimension query, by picking a third of

the dimension range. However, in practice we

empirically varied the dimension ranges in the

queries to get the desired DRR values.

The first test query had a condition on a single

dimension and a high DRR value of 0.37; the second

query had a lower DRR (0.05) with conditions on

two dimensions; and the third query had a very low

DRR (0.002) with conditions on all three

dimensions. The relevance of DRR in estimating the

query results may be seen from the query result

estimation process of Section 3.7. In step 3a, the

count 



directly depends upon the DRR, which is

the statistical proportion p whose estimate is given













. In step 3c, the estimation of sum depends

on the count 



and thereby on p.

We conducted the experiments using several

random samples at sampling rates of (1% - 12%) and

the results were averaged for each sampling rate.

The error for the three aggregate functions viz. avg,

sum and count were computed as the absolute value

of the difference between estimated and actual

values for the whole database. Figure 6 shows the

results with error rates for both average (mean) of

totscanamt column, sum of totscanamt and count for

the different database relevancy ratios mentioned

above.

There are two graphs for each level of DRR.

Figure 6a shows the error rates for the average, the

sum of scan amount and count for high DRR. Figure

6b shows the confidence intervals (lower and upper

limits) for the average amount for high DRR. Figure

6b also shows the estimated and actual values of the

average scan amount. Figures 6c and 6d show

similar information as above for the low value of

DRR; Figures 6e and 6f show similar information

for very low DRR.

It is seen that for the high DRR query with ρ(Q

)

= 0.37, the error rates for the count, average and the

sum of the total scan amount stabilize as the

sampling rate is increased. The estimates are close

−

′

−

′

sum

))((

)1(

−

)1(

)(

)1(

−

′

−

′

−

′

−

′

−

′

−

′

)1(

)(

)1(

−

′

−

′

−

′

−

′

−

′

−

′

AnEfficientSamplingSchemeforApproximateProcessingofDecisionSupportQueries

Figure 5: The schema for experimental retail sales data warehouse.

to the actual values for the lowest to the highest

sampling rates used and the true value of average is

always within the estimated confidence interval. For

the medium DRR query with ρ(Q

) = 0.05, we still

get error rates below the normally acceptable rate of

5%. For query with very low DRR of ρ(Q

) = 0.002,

the error rates for the average scan amount, for all

but 1% sampling rate, are below 5% and the true

values within the C.I. limits. But the error rates for

the estimated sum of scan amount and count of

records are not below the acceptable limit at any

sampling rate used for the very low DRR query.

Thus, we cannot satisfactorily estimate the sum and

the count for low values of DRR, while for medium

to high values of DRR the estimations of both the

sum and average are within acceptable error limits.

Also, it’s observed from the graphs that there is an

apparent close correlation between the estimates of

sum and count.

Time Improvement – Figure 7 shows the average

time for processing the queries at various sampling

rates and also the average time for processing these

queries on the full database. It is seen that there is a

significant time improvement from using the

sampling scheme.

5 CONCLUSIONS

In this paper, we proposed the k-MDI tree

indexwhich can be used to draw samples quickly for

answering multi-dimensional aggregate queries from

a data warehouse. The k-MDI tree extends the ACE

binary tree as a multi-way tree index. The maximum

number of levels of the k-MDI index is limited to the

number of key attributes and so makes the access to

the leaf nodes much quicker compared to a binary

tree index on external storage.

We also proposed the concepts of database

relevancy ratio (DRR) and sample relevancy ratio

(SRR) for queries. We investigated the effect of the

DRR on the accuracy of query results estimated

from samples drawn using the k-MDI index. From

the experimental evaluation of the sampling scheme

on a large real dataset, it is found that even at

relatively low sampling rates of 1% to 12 %, query

results can be estimated accurately with a minimum

of 95% confidence for queries with medium to high

DRR. At a very low DRR of 0.002, the estimated

values of sum and count fell outside the acceptable

confidence level of 95%, but the estimated mean

was within the 95% confidence interval even at very

low DRR. Depending on the sampling rate, the

sampling based query processing was on average 9

to 30 times faster than processing the same queries

against the whole dataset.

As future work, it is proposed to develop a

generic tool that can be used with some parameter

inputs to set up the k-MDI tree index for any data

warehouse schema. We also plan to further evaluate

the sampling based estimation scheme on data

warehouses with larger dimensions.

ITEMSCAN

storeno

datesold

itemno

visitno

qty

totalScanAmt

unitcost

unitprice

21,421,663

ITEMDESC

itemno

categoryno

subcategoryno

primarydesc

secondarydesc

colour

sizedesc

statuscode

19,825

STOREINFO

storeno

storename

regionno

districtno

storetype

address

150

STOREMEMBERVISTS

memberno

visitno

storeno

memberstatuscode

218,872

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

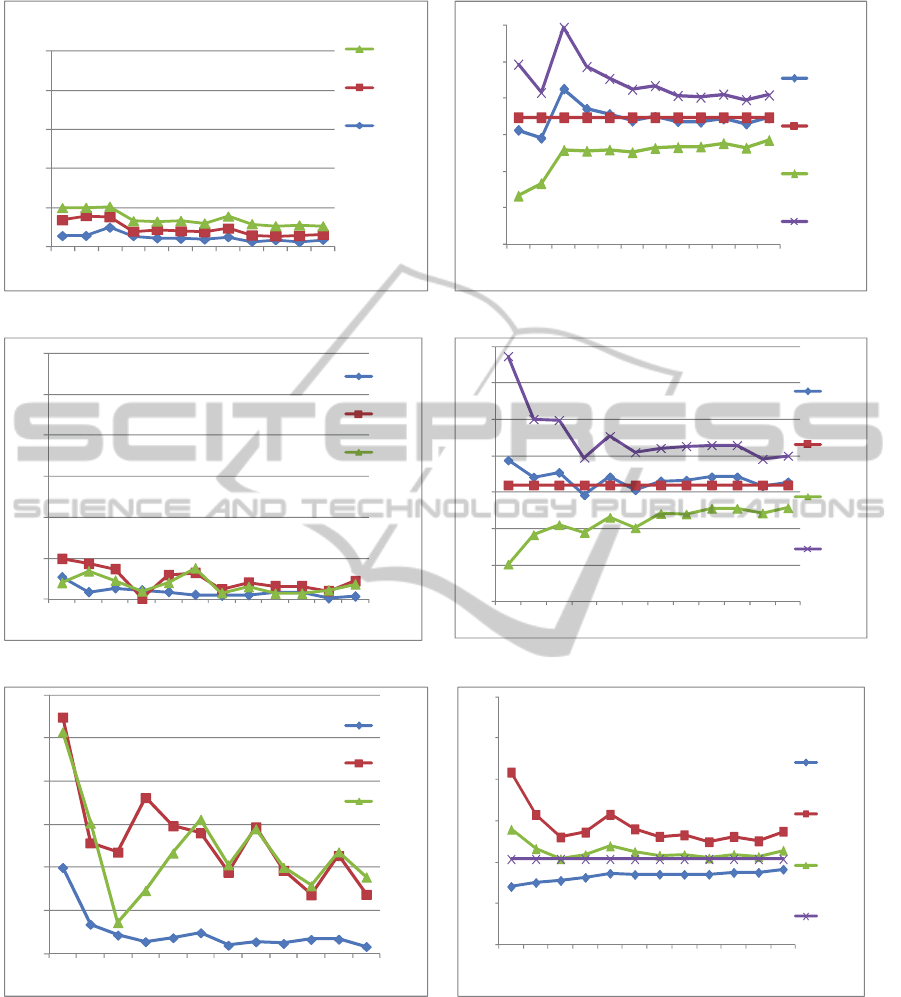
(a) Error rates for query with condition on one dimension (high

relevancy ratio).

(b) Confidence interval (AVG amt) for query with condition on

one dimension (high DRR).

(medium relevancy ratio).

(d) Confidence interval (AVG amt) for query with condition on

two dimensions (medium DRR).

(e) Error rates for query with condition on three dimensions (low

relevancy ratio).

(f) Confidence interval for query with condition on three

dimensions (low DRR).

Figure 6: Error rates of average scan amount and sum of scan amount and confidence interval of average scan amount at

various sampling rates for high, medium and low relevancy ratios.

123456789101112

Error rate (%)

Sampling rate (%)

Error rates - Average, Sum & Count

Err rate

Count

Err Rate

Sum Amt

Err Rate

Avg Amt

24.5

25.5

26.5

123456789101112

Avg Amt

Sampling rate (%)

Average amount and C.I. Limits - High DRR

Estimate of

AvgAmt

Actual Avg

Amt

C.I.Lwr

Limit Avg

Amt

C.I.Upper

Limit Avg

Amt

123456789101112

Error rate (%)

Sampling rate (%)

Error rates Avg, Sum & Count

Err Rate

Avg Amt

Err Rate

Sum Amt

Err rate

Count

123456789101112

Value

Sampling rate (%)

C.I. Limits for Avg Amt, Actual vs Estimate

Estimat

e of

AvgAmt

Actual

Avg Amt

C.I.Lwr

Limit

Avg Amt

C.I.Uppe

r Limit

Avg Amt

123456789101112

Error rate (%)

Sampliing rate (%)

Error rates - Average, Sum & Count

Err Rate

Avg Amt

Err Rate

Sum Amt

Err rate

Count

123456789101112

Avg Amt

Sampling rate (%)

Average amount and C.I. Limits - Low DRR

C.I.Lower

Limit

C.I.Upper

Limit

Estimate

of Avg

Amt

Actual

Avg Amt

AnEfficientSamplingSchemeforApproximateProcessingofDecisionSupportQueries

Figure 7: Query times at different sampling rates as

compared to full database scan.

REFERENCES

Berenson, M. L., Levine, D. M., 1992. Basic Business

Statistics - Concepts and Applications. Prentice Hall,

Upper Saddle River, New Jersey, USA.

Bernardino, J., Furtado, P., Madeira, H., 2002.

Approximate Query Answering Using Data

Warehouse Striping. Journal of Intelligent Information

Systems. 19:2, pp.145-167.

Chaudhuri, A., Mukherjee, R., 1985. Domain Estimation

in Finite Populations. Australian Journal of Statistics.

Vol. 27:2, pp. 135-137.

Hellerstein, H, Haas, P, Wang, J., 1997. Online

Aggregation. SIGMOD 1997, pp. 171-182.

Hobbs, L., Hillson, S., Lawande, S., 2003. Oracle9iR2

Data Warehousing. Elsevier Science, MA, USA.

Jermaine, C., 2007. Random Shuffling of Large Database

Tables. IEEE Transactions on Knowledge and Data

Engineering. 18:1, pp.73-84.

Jermaine, C., 2003. Robust Estimation with Sampling and

Approximate Pre-Aggregation. VLDB Conference

Proceedings 2003, pp. 886-897.

Jermaine, C., Pol, A., Arumugam, S., 2004. Online

Maintenance of Very Large Random Samples.

SIGMOD Conference Proceedings 2004.

Jin, R., Glimcher, L, Jermaine, C, Agrawal, G., 2006. New

Sampling-Based Estimators for OLAP Queries.

Proceedings of the 22

International Conference on

Data Engineering (ICDE'06), Atlanta, GA, USA.

Joshi, S., Jermaine, C., 2008. Materialized Sample Views

for Database Approximation, IEEE Transactions on

Knowledge and Data Engineering, 20:3 pp. 337-351.

Keller, G., 2009. Statistics for Management and

Economics. Cengage Learning, Mason, OH, USA.

Kimball, R., Ross, M., 2002. The Data Warehouse

Toolkit: The Complete Guide to Dimensional

Modeling, 2nd Ed. John Wiley & Sons, Indianapolis,

USA.

Li, X., Han, J., Yin, Z., Lee, J-G., Sun, Y., 2008.

Sampling Cube: A Framework for Statistical OLAP

over Sampling Data. Proceedings of ACM SIGMOD

International Conference on Management of Data

(SIGMOD'08), Vancouver, BC, Canada, June.

Olken, F., Rotem, D., 1990, Random Sampling from

Database File. In: A Survey. International Conference

on Scientific and Statistical Database Management,

1990. pp. 92-111.

Spiegel, J., N. Polyzotis, 2009. TuG Synopses for

Approximate Query Answering. ACM Transactions on

Database Systems. (TODS) 34(1).

TPC Benchmarks, 2011. Transaction Processing

Performance Council - TPC-H: Decision Support

Benchmark. http://www.tpc.org [Accessed 20

November 2011].

TUN - Teradata University Network, 2011.

http://www.teradata.com/TUN_databases. [Accessed:

13 April 2007].

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems