
Using Formal Concept Analysis to Extract a Greatest Common Model
Bastien Amar
1
, Abdoulkader Osman Guédi
1,2,3
, André Miralles
1,3
,
Marianne Huchard
3
, Thérèse Libourel
4
and Clémentine Nebut
3
1
Tetis/IRSTEA, Maison de la Télédétection, 500 Rue J.-F. Breton 34093, Montpellier Cdx 5, France
2
Université de Djibouti, Avenue Georges Clemenceau, BP 1904, Djibouti, Republic of Djibouti
3
LIRMM, Univ. Montpellier 2 et CNRS, 161, rue Ada, F-34392, Montpellier Cdx 5, France
4
Espace Dev, Maison de la Télédétection, 500 Rue J.-F. Breton 34093, Montpellier Cdx 5, France
Keywords:
Formal Concept Analysis, FCA, Greatest Common Model, GCM, Pesticide, Environmental Information
System, Model Factorization, Core-concept, Domain-concept.
Abstract:
Data integration and knowledge capitalization combine data and information coming from different data
sources designed by different experts having different purposes. In this paper, we propose to assist the under-
lying model merging activity. For close models made by experts of various specialities, we partially automate
the identification of a Greatest Common Model (GCM) which is composed of the common concepts (core-
concepts) of the different models. Our methodology is based on Formal Concept Analysis which is a method
of data analysis based on lattice theory. A decision tree allows to semi-automatically classify concepts from
the concept lattices and assist the GCM extraction. We apply our approach on the EIS-Pesticide project, an en-
vironmental information system which aims at centralizing knowledge and information produced by different
specialized teams.
1 INTRODUCTION AND
PROBLEMATICS
Elaborating data models is a recurrent activity in
many projects in different domains, for various ob-
jectives: building dictionaries of the domain, design-
ing databases, developing software for this domain,
etc. Usually, such models of the domain are required
by several teams, dealing with different facets of the
domain, and potentially stemming from different sci-
entific domains. For example, in the IRSTEA insti-
tute (in which three of the authors work), the study of
pesticide impact on environment involves specialists
from different scientific domains: hydrology, agron-
omy, chemistry, etc.
Each specialist is able to model the part of the do-
main model it is familiar with, and finally, a consol-
idated domain model must be built gathering all the
specialized models. This gathering activity is com-
plex and generally carried out manually. Indeed, it re-
quires to detect the common domain-concepts mod-
eled in the various specialized models, so as to in-
tegrate them without redundancy in the consolidated
model named greatest common model (GCM). This
GCM is particularly useful to perform schema inte-
gration and knowledge capitalization.
In this paper, we address the issue of assisting
this gathering activity, in the context of domain data
models designed with UML class diagrams through
the automated detection of common domain-concepts
(with two levels of confidence) possibly enriched with
new domain-concepts automatically extracted from
the previous ones. This approach is based on For-
mal Concept Analysis (FCA), which is an exact and
robust data analysis method based on lattice theory.
We use FCA to detect commonalities, redundancies
and introduce new abstractions, both inside the mod-
els taken individually (intra-model factorization), and
inside two distinct data models taken jointly (inter-
model factorization). The approach defined in this
paper deals with two models, but more generally, it
is able to identify the common domain-concepts of
several models in order to help the designer to cen-
tralize these common concepts into a unique consoli-
dated model (the GCM). This approach is under eval-
uation on a large project from the IRSTEA institute
called Environmental Information System for Pesti-
cides (EIS-Pesticides), in which two teams cooperate
27
Amar B., Osman Guédi A., Miralles A., Huchard M., Libourel T. and Nebut C..
Using Formal Concept Analysis to Extract a Greatest Common Model.
DOI: 10.5220/0003996000270037
In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 27-37
ISBN: 978-989-8565-10-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

to build a domain data model. The transfer team is
specialized in the study of the pesticides transfer to
the rivers and the practice team, mainly works on the
agricultural practices of farmers.
The rest of the paper is structured as follows. In
Section 2 we introduce example models taken from
the EIS-Pesticides project. In Section 3, we draw the
main lines of our approach, and in Section 4, we pro-
vide a short introduction to Formal Concept Analysis
(FCA). In Section 5 we explain how FCA is used on
input models and how the resulting lattices are an-
alyzed so as to provide the final user clear recom-
mendations to build the greatest common model. In
Section 6, we present our produced greatest common
model of our example models and we apply our ap-
proach on a larger model to evaluate its scalability.
Section 7 presents the related work and Section 8 con-
cludes the paper.
2 RUNNING EXAMPLE: THE
TWO MODELS OF
MEASURING STATION
The Environmental Information System for Pesticides
(EIS-Pesticides) is a project (Pinet et al., 2010; Mi-
ralles et al., 2011) that has the objective to set up an
information system allowing to centralize knowledge
and information produced by Transfer and Practice
teams (see Section 1). We illustrate our approach on
a small subsystem representing part of the measuring
activity on the catchment area (drainage basin): mea-
suring stations monitor the major parameters involved
in the transfer of the pesticides to the rivers.
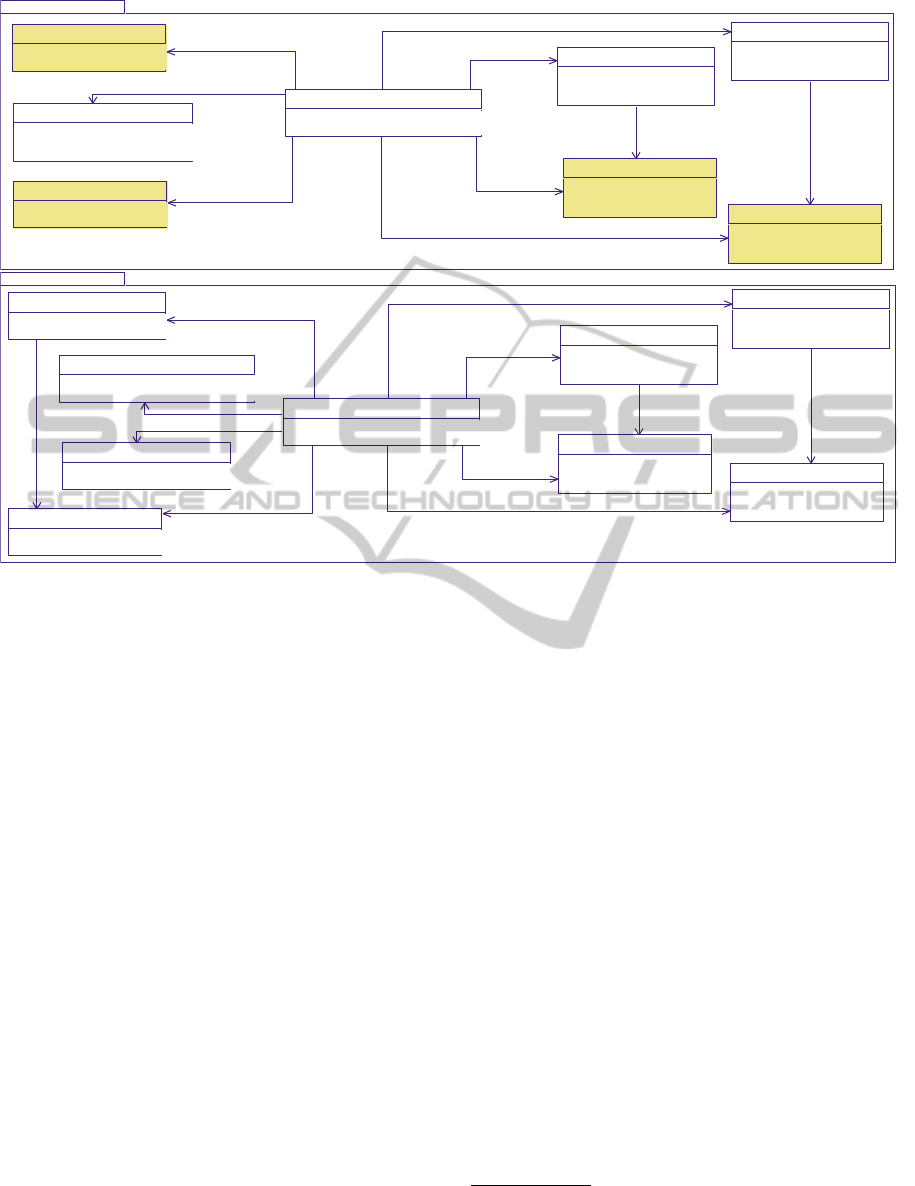
Figure 1 shows the two data models of the mea-
suring stations used in this study. They are pro-
duced by the two teams involved in the project.
As these two models are very close, we have or-
ganized them by grouping at the r.h.s of mea-
suring station (cl_MeasuringStation), the identical
domain-concepts (that also have the same relation-
ships). In this part of the model, the measured
data are associated to the corresponding measur-
ing device: the rainfall (cl_Rainfall) and the hy-
draulic head (cl_HydraulicHead) of the ground-
water table are continuously recorded respectively
by the rain gauge (cl_RainGauge) and by the
piezometer (cl_Piezometer). Each of these mea-
sures is dated (see property att_MeasuringDate).
On the l.h.s. of cl_MeasuringStation, the model
M1_MeasuringStation allows to record the data
measured by a weather station of Météo-France
(a french meteorological institute): temperature
(cl_Temperature), hygrometry (cl_Hygrometry) and
potential evapo-transpiration (cl_PET) of the short
green crops. These last domain-concepts are not in
the model M2_MeasuringStation which has on the
other hand a limnimeter (cl_Limnimeter) to measure
continuously the flow rate (cl_FlowRate) of rivers. A
technician is in charge to take samples in order to de-
termine in laboratory the amount of pesticides in the
water (cl_PesticideMeasurement). Finally, the wind
velocity (cl_WindMeasurement) is a parameter com-
ing from a weather station of Météo-France.
3 OVERVIEW OF THE
PROPOSED APPROACH
The main objective of our approach is to assist the
task of gathering two or more models independently
defined and thus potentially involving common con-
cepts. For that we extract from initial models their
Greatest Common Model (GCM). The term "greatest
common model" is chosen by analogy to the "greatest
common divisor (GCD)" in arithmetic; it is more pre-
cisely defined in the following. Roughly, it contains
all the common domain-concepts that are introduced
in all the studied models, in a normal
1
(factorized)
form.
The proposed approach is illustrated in Figure 2.
The input is two (or more) models for a domain,
named M
1
and M
2
. In a first time, the classes of the
input models are described by their owned character-
istics. Formal Concept Analysis (FCA) allows enti-
ties sharing characteristics to be grouped into formal-
concepts, and results in lattices providing a hierarchi-
cal view of those formal-concepts. We apply FCA
on several class descriptions, resulting in several lat-
tices. These lattices allow the identification of com-
mon concepts, specific concepts and eventually new
abstractions extracted from intra- or inter- model fac-
torization. For instance, if we describe classes by their
owned attributes, the resulting lattice (cf Figure 5)
extracts the r.h.s. common domain concepts of Fig-
ure 1. It also extracts new abstractions. Some new
abstractions are present both in M
1
and M
2
(e.g. a de-
vice concept factorizes commonalities of rain gauge,
and piezometer: inter-model factorization). Some
other extracted abstractions are present only in a same
model (e.g. a dated measurement concept factorizes
pesticide and wind measurements in M
2
: intra-model
factorization). For each lattice, we have two levels
1
Here, we refer to the relational normal form used in
database schema normalization, which has the same objec-
tive: eliminate redundancies.
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
28
M2_MeasuringStation
M1_MeasuringStation
0..1
1
ro_DeviceRainfall Instrumentation
ro_Station
*
0..1
ro_Measure
Rainfall Information
ro_Station
*
0..1
ro_Measure
Groundwater Information
ro_Station
0..1
1
ro_Device
Groundwater Instrumentation
ro_Station
*
0..1
ro_Rainfall
Rainfall Monitoring
ro_RainGauge
*
0..1
ro_HydraulicHead
Groundwater Monitoring
ro_Piezometer
*
0..1
ro_Rainfall
Rainfall Monitoring
ro_RainGauge
*
0..1
ro_Measure
Rainfall Information
ro_Station
0..1
1
ro_Device
Rainfall Instrumentation
ro_Station
*
0..1
ro_HydraulicHead
Groundwater Monitoring
ro_Piezometer
*
0..1
ro_Measure
Groundwater Information
ro_Station
0..1
1
ro_Device
Groundwater Instrumentation
ro_Station
*
0..1
ro_Measure
Wind Information
ro_Station
*
0..1
ro_Measure
Pesticide Information
ro_Station
*
0..1
ro_Measure
Water Height Information
ro_Station
0..1
1
ro_Device River gauging
ro_Station
*
0..1
ro_FlowRate
Water Height Monitoring
ro_Limnimeter
*
0..1
ro_Humidity
Hygrometry Information
ro_Station
*
0..1
ro_Measure ETP Information
ro_Station
*
0..1
ro_Measure
Temperature Information
ro_Station
cl_Rainfall
cl_HydraulicHead
cl_RainGauge
cl_Piezometer
cl_WindMeasurement
cl_PesticideMeasurement
cl_FlowRate
cl_Limnimeter
cl_MeasuringStation
cl_Rainfall
cl_RainGauge
cl_HydraulicHead
cl_Piezometer
cl_Temperature
cl_Hygrometry
cl_PET
cl_MeasuringStation
att_CodeQuality : string
att_MeasuringDate : string
att_WaterAmount : real
att_CodeQuality : string
att_MeasuringDate : string
att_WaterHeight : real
att_TubeHeight : real
att_DeviceNumber : integer
att_DeviceType : string
att_TubeDiameter : real
att_DeviceNumber : integer
att_DeviceType : string
att_Velocity : real
att_Date : string
att_Quantity : real
att_Date : string
att_MeasuringDate : string
att_WaterHeight : real
att_DeviceNumber : integer
att_DeviceType : string
att_AdministrativeInstitute : string
att_StationName : string
att_CodeQuality : string
att_MeasuringDate : string
att_WaterAmount : real
att_TubeHeight : real
att_DeviceNumber : integer
att_DeviceType : string
att_CodeQuality : string
att_MeasuringDate : string
att_WaterHeight : real
att_TubeDiameter : real
att_DeviceNumber : integer
att_DeviceType : string
att_Value : integer
att_MeasuringHour : string
att_Volume : integer
att_Weight : real
att_MeasuringDateHour : string
att_Value : integer
att_MeasuringHour : string
att_AdministrativeInstitute : string
att_StationName : string
Figure 1: The two data models of measuring station produced by the two teams.
of confidence for those domain-concepts: domain-
concepts which are very likely to be in the GCM, and
others that have to be precisely analyzed, validated
and named by the final expert. As we generate sev-
eral lattices, the expert in charge of integration needs
to follow a strategy for analyzing them. We propose
to order the obtained lattices following the semantic
hierarchy of the different factorization criteria. The
lattices are then analyzed, so as to categorize formal-
concepts and interpret them, if applicable, to form
domain-concepts.
The domain-concepts recognized by the experts
as being in the GCM are called the core domain-
concepts. In Figure 1, the domain-concepts to
the right of cl_MeasuringStation are certainly core
domain-concepts. The greatest common model
(GCM) is defined as the largest model factorizing the
core domain-concepts of several models.
4 A SHORT INTRODUCTION TO
FORMAL CONCEPT ANALYSIS
Formal Concept Analysis (FCA) (Ganter and Wille,
1999) is a method of data analysis based on lattice
theory (Birkhoff, 1940). It is used in many appli-
cations relative to classification including knowledge
structuring, information retrieval, association rule ex-
traction in the data mining domain, class model refac-
toring, or software analysis. FCA studies entities
described by their characteristics to discover formal-
concepts which are maximal groups of entities shar-
ing maximal groups of characteristics. A partial spe-
cialization order based on the entity set inclusion pro-
vides a lattice structure (the concept lattice).
A formal context K is a triple
2
K = (E,C, R),
where E is the set of entities and C the set of char-
acteristics that describe these entities. R ⊆ E ×C as-
sociates an entity with its characteristics: (e, c) ∈ R
when entity e owns characteristic c. For example, Ta-
ble 1 shows the formal context of the sub-model high-
lighted in Figure 1 (limited to the four classes cl_PET,
cl_Temperature, cl_HydraulicHead and cl_Rainfall).
Classes (the entities) are described by the name of
their owned attributes (characteristics).
A formal-concept is a pair (Extent, Intent)
where Extent = {e ∈ E|∀c ∈ Intent, (e, c) ∈ R} and
Intent = {c ∈ C|∀e ∈ Extent, (e, c) ∈ R}. These
two sets represent the entities that own all the
characteristics (extent) and the characteristics shared
2
In the literature, standard notation is K = (G, M, I). We
use K = (E,C, R) for readability reasons and to get a better
understanding toward our thematic partners.
UsingFormalConceptAnalysistoExtractaGreatestCommonModel
29

FCA Based
analysis
M1 M2
GCM Specific
Concepts
M1
M2
: New Abstractions
Figure 2: A schematic overview of our approach (applied
on one formal context).
Table 1: The formal context of the reduced model.
att_MeasuringHour
att_Value
att_WaterAmount
att_MeasuringDate
att_CodeQuality
att_WaterHeight
cl_PET × ×
cl_Temperature × ×
cl_Rainfall × × ×
cl_HydraulicHead × × ×
by all entities (intent). The specialization or-
der between two formal concepts is given by
the following equivalence: (Extent_1, Intent_1) <
(Extent_2, Intent_2) ⇔ Extent_1 ⊂ Extent_2 (equiv-
alently Intent_2 ⊂ Intent_1).
In a lattice, there is an ascending inheritance of en-
tities and a descending inheritance of characteristics.
The simplified intent of a formal concept is its intent
without the characteristics inherited from its super-
concept intents. The simplified extent is defined in
a similar way.
Nota: in this article, we distinguish simplified ex-
tent from extent. When it is not specified, we are talk-
ing about (complete) extent.
For readability reasons, all lattices presented in
this paper show simplified extents and intents.
Figure 3 shows the concept lattice built from
the formal context presented Table 1. Each formal-
concept is represented by a box in three parts: the
first contains the generated name of the formal-
concept, the second part contains its simplified in-
tent, and the last one contains its simplified ex-
tent. Let us consider Concept_17: it repre-
sents entities (classes) described by the characteris-
tic att_WaterHeight and by the characteristics inher-
ited from its super-concepts: att_MeasuringDate and
att_CodeQuality (from Concept_16).
Intent
Extent
Concept_13
att_MeasuringHour
att_Value
cl_PET
cl_Temperature
M
Concept_17
att_WaterHeight
cl_HydraulicHead
P
Concept_14
N
Concept_15
att_WaterAmount
cl_Rainfall
P
Concept_16
att_MeasuringDate
att_CodeQuality
N
Concept_12
N
Figure 3: Class/attribute name lattice: result of FCA on Ta-
ble 1.
In this work, we are interested in three categories
of formal-concepts that form a partition of the set of
formal-concepts:
Definition 1. Merged formal concepts have more
than one entity in their simplified extent. This means
that all entities in the extent are described by exactly
the same set of characteristics.
In Figure 3, Concept_13 is a merged formal con-
cept: cl_PET and cl_Temperature are (exactly) de-
scribed by both characteristics att_MeasuringHour
and att_Value.
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
30

Definition 2. New formal concepts have an empty
simplified extent. These are new, more abstract, con-
cepts, factoring out characteristics common to several
formal-concepts.
In Figure 3, Concept_16 is a new formal concept,
factoring out characteristics of both Concept_15 and
Concept_17.
Definition 3. Perennial formal concepts have one and
only one entity in their simplified extent.
In Figure 3, both Concept_15 and Concept_17
are perennial. In this article, merged, new and peren-
nial formal concepts are respectively annotated, in the
figures, M, N and P at the right-top corner.
5 APPLYING FORMAL
CONCEPT ANALYSIS TO
EXTRACT CANDIDATES FOR
THE GREATEST COMMON
MODEL
In this section, we propose a methodology based on
two automatic steps that uses Formal Concept Analy-
sis (FCA) and an interactive step to extract the great-
est common model of two input models. Given two
models M
1
and M
2
:
• We compute the lattices resulting from FCA ap-
plied to several formal contexts extracted from the
disjoint union of the two input models
M = M
1
⊕ M
2
.
• The concepts of these lattices are analyzed thanks
to a decision tree based on the analysis of the con-
cept extent, and we obtain six concept lists (cate-
gories).
In the interactive step, these six lists are exploited to
assist the expert to build the greatest common model.
The next subsections precisely describe two auto-
matic steps.
5.1 Apply FCA on the Two Models
As explained in Section 4, formal contexts describe
entities by characteristics. Many different formal con-
texts can be extracted from a class model: it has to be
defined which model elements are chosen to be the
studied entities, and which features of those model
elements are chosen to be their studied characteris-
tics. Here we focus on three formal contexts extracted
from the disjoint union of input models M = M
1
⊕M
2
:
1. the formal context of classes described by their
name,
2. the formal context of classes described by their
attributes,
3. the formal context of classes described by their
attributes and by their roles.
Figure 4 presents the lattice obtained with the formal
context of classes described by their name (class/class
name lattice). This lattice groups in a concept the
set of classes sharing the same name. For exam-
ple, the merged concept Concept_1 represents the
set of classes (in extent) sharing the name (in intent)
cl_Piezometer. In other words, FCA merged in a sin-
gle concept classes that have a same name. Classes
that are not duplicated in the models M
1
and M
2
re-
main in a perennial concept, like the cl_PET class in
Concept_7. In inter-model factorization, the three
categories of concepts described in Section 4 exist:
the merged concept Concept_1 has more than one
entity in its simplified extent. In a similar way, the
perennial concept Concept_7 (cl_PET) has exactly
one element in its extent. Later we will see the case
where new formal concepts appear.
Figure 5 presents the lattice obtained with the for-
mal context of classes described by the names of
their owned attributes (class/attribute name lattice).
In this lattice, a formal concept thus is a group of
classes (extent) sharing a group of attribute names
(intent). The lattice contains new formal concepts
(simpli f ied extent =
/
0), e.g. Concept_47, that rep-
resents a new abstraction: things that are dated.
Figure 6 presents the lattice obtained with the for-
mal context of classes described by the names of their
owned attributes and roles (class/attribute-role name
lattice). UML associations are taken into account in
this lattice through those roles. For example, class
cl_FlowRate has attribute att_WaterHeight and role
ro_Station in association Water Height Information.
The new formal concept Concept_30 represents the
classes that are linked with a Station via the role
ro_Station. Class cl_FlowRate belongs to the extent
of this concept.
5.2 Analysis of the Lattices
In this section, we present the analysis of the lattices
using a decision tree to classify each concept. First,
the class/class name lattice must be analyzed. This
lattice allows the designer to group classes that have
a same name. Then, we analyze the class/attribute
name lattice that allows us to find attribute-based fac-
torizations. As we will see, the class/attribute-role
name lattice can be a considerable help to refine the
decisions about factorization.
For each formal concept Co
k
= (E
k
, I
k
), the com-
plete extent E
k
has to be analyzed and the concept has
UsingFormalConceptAnalysistoExtractaGreatestCommonModel
31

Concept_1
cl_Piezometer
cl_Piezometer
cl_Piezometer
Concept_3
cl_HydraulicHead
cl_HydraulicHead
cl_HydraulicHead
Concept_4
cl_RainGauge
cl_RainGauge
cl_RainGauge
Concept_6
cl_MeasuringStation
cl_MeasuringStation
cl_MeasuringStation
Concept_8
cl_Hygrometry
cl_Hygrometry
Concept_9
cl_Temperature
cl_Temperature
Concept_10
cl_Limnimeter
cl_Limnimeter
Concept_12
cl_PesticideMeasurement
cl_PesticideMeasurement
Concept_13
cl_WindMeasurement
cl_WindMeasurement
Concept_0
N
M
M M M
P
P P P P
Concept_5
cl_Rainfall
cl_Rainfall
cl_Rainfall
M
Concept_7
cl_PET
cl_PET
P
Concept_11
cl_FlowRate
cl_FlowRate
P
Concept_2
N
Figure 4: The class/class name concept lattice.
Concept_35
att_DeviceType
att_DeviceNumber
cl_Limnimeter
Concept_36
att_TubeDiameter
cl_Piezometer
cl_Piezometer
Concept_40
cl_HydraulicHead
cl_HydraulicHead
Concept_42
att_TubeHeight
att_TubeHeight
cl_RainGauge
cl_RainGauge
Concept_43
att_WaterAmount
cl_Rainfall
cl_Rainfall
Concept_44
att_StationName
att_AdministrativeInstitute
cl_MeasuringStation
cl_MeasuringStation
Concept_45
att_MeasuringHour
att_Value
cl_PET
cl_Temperature
Concept_46
att_MeasuringDateHour
att_Weight
att_Volume
cl_Hygrometry
Concept_48
att_Quantity
cl_PesticideMeasurement
Concept_49
att_Velocity
cl_WindMeasurement
Concept_38
att_WaterHeight
cl_FlowRate
Concept_39
att_MeasuringDate
Concept_41
att_CodeQuality
M
M
M
M
M
P
P
P
P
Concept_34
N
N
N
P
M
Concept_37
N
Concept_47
att_Date
N
Figure 5: The class/attribute name concept lattice.
to be included in one of these lists:
• L
GCM
is the list of core-concepts that will be in-
cluded in the greatest common model.
• L
pGCM
is the list of potential (candidate) core-
concepts to be validated by an expert to be in the
greatest common model.
• L
M
1
and respectively L
M
2
are the lists of domain
concepts specific to M
1
(resp. M
2
).
• L
nM
1
and respectively L
nM
2
are new domain con-
cepts specific to M
1
(resp. M
2
), factorizing exist-
ing domain concepts. These domain concepts are
not intended to be in the greatest common model,
but they can be presented to experts to improve
the factorization of M
1
(resp. M
2
).
Figure 7 presents the decision tree: we define C
M
i
(resp. C
M
j
) as the set of classes in the model M
i
(resp.
M
j
), and the decision tree is designed for two mod-
els M
i
and M
j
where i 6= j. As we apply FCA with
classes as entities (characteristics being class name,
attributes, and/or roles), the extent of a concept con-
tains only classes. For each concept, we first check if
the concept is a merged concept, a new concept or a
perennial concept (nodes 1, 8 and 12 in the decision
tree of Figure 7) as defined in Section 4.
Analysis of Merged Concepts: If the concept is a
merged concept, then three cases are possible: its ex-
tent contains elements from both models M
i
and M
j
(node 2), its extent contains only elements from M
i
(node 6), or its extent is empty (node 7).
If the concept extent contains elements from both
models, the cardinality of the intersection between
the extent and the set of model classes has to be
checked. In the first case, the extent contains only
one class from M
i
and only one class from M
j
(node
3) like Concept_1 in the class/class name lattice, Fig-
ure 4. Then a corresponding domain concept should
be added in L
GCM
: it can be considered as a core-
concept – a domain concept common to both mod-
els. If the extent contains only one class from M
i
and several classes from M
j
(node 4), or several el-
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
32

Concept_15
att_DeviceType
att_DeviceNumber
Concept_16
att_TubeDiameter
ro_HydraulicHead
cl_Piezometer
cl_Piezometer
Concept_20
ro_Piezometer
cl_HydraulicHead
cl_HydraulicHead
Concept_23
att_WaterAmount
ro_RainGauge
cl_Rainfall
cl_Rainfall
Concept_25
att_MeasuringHour
att_Value
cl_PET
cl_Temperature
Concept_26
att_MeasuringDateHour
att_Weight
att_Volume
cl_Hygrometry
Concept_28
att_Quantity
cl_PesticideMeasurement
Concept_29
att_Velocity
cl_WindMeasurement
Concept_31
ro_Humidity
cl_MeasuringStation
Concept_18
att_WaterHeight
Concept_19
att_MeasuringDate
Concept_21
att_CodeQuality
Concept_24
att_StationName
att_AdministrativeInstitute
ro_Device
ro_Measure
cl_MeasuringStation
P
P
P
PP
N
N N
N
M
M
M
M
Concept_14
N
Concept_30
ro_Station
N
Concept_27
att_Date
N
Concept_33
ro_Limnimeter
cl_FlowRate
P
Concept_32
ro_FlowRate
cl_Limnimeter
P
Concept_22
att_TubeHeight
att_TubeHeight
ro_Rainfall
cl_RainGauge
cl_RainGauge
M
Concept_17
N
Figure 6: The class/attribute-role name concept lattice.
ements from both models (node 5), then it should be
put in the L
pGCM
list: it is a potential core-concept,
but an expert intervention is necessary. He or she can
choose to merge or factorize duplicated classes if they
are semantically closed, in a same model (intra-model
factorization), and relaunch the process to extract the
greatest common model. He or she can also consider
these classes as specific domain concepts and keep
them in the specific model.
If the merged concept contains only classes from
M
i
(node 6), like the Concept_45 in the Figure 5, it
should be added to the L
nM
i
list. Its extent contains
a group of elements coming from a same model and
that are described exactly by the same characteristics.
It can be presented to an expert to improve the model
M
i
, but it is not a core-concept (they are in one model
only). In the case of Concept_45, FCA suggests to
merge the classes cl_PET (representing the Poten-
tial Evapo-Transpiration) and cl_Temperature. In this
special case, these two classes are semantically differ-
ent, and the expert do not want to factorize them, but
in other situations he could consider this factorization
to be interesting.
The node 7 describes concepts wherein the extent
does not contain classes from M
i
and M
j
. This is
inconsistent: by definition, a merged concept extent
contains at least two elements (cf definition 1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Figure 7: Decision tree.
Analysis of New Concepts: If the concept is a new
concept (cf. definition 2, node 8), and if its extent
contains elements from both models M
i
and M
j
(node
9) then the concept has to be put in the L
pGCM
list: it is
a potential factorization of concepts defined in M
i
and
M
j
, so it is potentially a core-concept. Experts have
to decide if this factorization is valid and if this new
concept has to be included in the greatest common
model. Concept_39 in Figure 5 is an example of this
type of concept. In our case study, the expert validates
UsingFormalConceptAnalysistoExtractaGreatestCommonModel
33

this concept to be a greatest common model concept.
If the new concept extent contains only classes
from one model, it can be added in the L
nM
i
list
(node 10 in the decision tree). This concept corre-
sponds to an intra-model factorization. It is the case
of Concept_47, representing things that are dated in
M
2
. This kind of concept is not a core-concept and
should not be included in the greatest common model.
It can be presented to the M
i
designer in order to raise
the quality of its model by a new factorization.
If the new concept extent (node 11 in the decision
tree) does not contain elements from M
1
nor M
2
, this
means that this is the concept Bottom. Concept Bot-
tom is present in each lattice (concepts Concept_2,
Concept_37 and Concept_17). It represents ele-
ments that own all attributes and should not be used
in our re-engineering process. Instead, the top con-
cept can not be inferred only by extent analysis and it
may appear in each branch of the tree. Depending on
the configuration of the models analyzed, this concept
may be relevant and it is classified as other concepts.
Analysis of Perennial Concepts: Node 13 in the
decision tree describes perennial concepts that have in
their extent classes from M
i
and M
j
, like Concept_35
in Figure 5. This means that there is a potential fac-
torization of Concept_36 and Concept_42, and this
factorization already exists, cl_Limnimeter in our ex-
ample. This kind of concept has to be presented to
the expert, it is thus added to the L
pGCM
list. In our
example, the designer can make cl_limnimeter be a
super-class of cl_piezometer and cl_Raingauge, but
this decision is not semantically valid: a piezome-
ter is not a limnimeter. An analysis of the lattice of
classes described by their attributes and role names
(Figure 6) shows that it is better to create a new super-
class (Concept_15) of data instrumentation, factor-
izing the three classes cl_limnimeter, cl_Piezometer
and cl_RainGauge. In this case, the lattice of classes
described by their attributes/roles names is useful to
help the designer to take a decision.
If the perennial concept extent contains only
classes from M
i
(node 14) then it is a M
i
domain
specific concept. This concept must be added to
L
M
i
. For example, concepts Concept_7, Concept_8,
Concept_48, and Concept_46 are domain concepts
specific to M
i
.
A perennial concept cannot have an empty extent
(node 15): the definition 3 specifies that a perennial
concept has one (and only one) element in its extent.
From both L
GCM
and L
pGCM
lists, the expert has
to select the core-concepts that will be included in the
GCM.
Our approach has been implemented as a profile in
a case tool. A component transforms the UML mod-
els into the different types of formal contexts which
are entries of FCA. Another component produces the
corresponding lattices. Finally, another component
generates the various lists of domain-concepts in ac-
cordance with the decision tree.
6 RESULTS
Figure 8 shows the model obtained by applying our
approach: the final greatest common model of the M1
and M2 models (Figure 1). This GCM reflects also
the interpretation and the validation by an expert of
the new concepts. We annotated classes by associ-
ated formal concepts that represent them in the lat-
tices (Figures 4, 5 and 6).
As expected, the same domain-concepts in
both models M1 and M2 are present in the
GCM: cl_MeasuringStation, cl_Piezometer,
cl_HydraulicHead, cl_RainGauge and cl_Rainfall.
They constitute the core-concepts of the GCM of
M1 and M2. So, they are automatically added in the
L
GCM
list.
Our approach proposes a list of possible factoriza-
tions of domain-concepts in the L
pGCM
list. The ex-
pert must validate the relevance of these concepts. In
this example, two new concepts have been considered
relevant. They are colored in figure 8.
The first corresponds to formal concepts
Concept_15 (Figure 6) and Concept_35 (Fig-
ure 5) in the lattices. They factorize attributes
att_DeviceType and att_DeviceNumber. This concept
has been validated by experts as a new cl_Device
class.
The second new concept corresponds to formal
concepts Concept_41 and Concept_21 in the lat-
tices. It factorizes both att_MeasuringDate and
att_CodeQuality attributes. Similarly to the first
new concept, experts validate this concept as a new
cl_Data class.
Table 2 quantifies for each formal context the
number of concepts in each list defined in the deci-
sion tree
3
.
In order to validate the scalability of our approach,
tests have been done on two versions of the com-
plete model from the EIS-pesticides project (about
125 classes). Table 3 gives the number of concepts
by list of the decision tree
3
.
With the class/class name and class/attribute name
lattices, experts have to analyze and to validate be-
tween 34 and 39 concepts present in the L
pGCM
list.
3
In these tables, new and merged concepts must be still
validated by an expert.
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
34

Greatest Common Model
ro_Station
Groundwater Instrumentation
ro_Device
1
0..1
ro_Station
Rainfall Instrumentation
ro_Device
1
0..1
ro_Station
Groundwater Information
ro_Measure
0..1
*
ro_Station
Rainfall Information ro_Measure
0..1
*
ro_RainGauge
Rainfall Monitoring
ro_Rainfall
0..1
*
ro_Piezometer
Groundwater Monitoring
ro_HydraulicHead
0..1
*
cl_Data
cl_Device
cl_MeasuringStation
cl_HydraulicHead
cl_Piezometer
cl_Rainfall
cl_RainGauge
att_CodeQuality : string
att_MeasuringDate : string
att_DeviceNumber : integer
att_DeviceType : string
att_AdministrativeInstitute : string
att_StationName : string
att_WaterHeight : real
att_TubeDiameter : real
att_WaterAmount : real
att_TubeHeight : real
Concepts 41, 21
Concepts 5, 43, 23
Concepts 15, 35
Concepts 2, 22, 42
Concepts 1, 16, 36
Concepts 6, 31, 44
Concepts 3, 20, 40
Figure 8: The greatest common model of M1 and M2 models (Figure 1).
Table 2: Result of our approach on the MeasuringStation model.
L
GCM
L
pGCM
L
nM1
L
nM2
L
M1
L
M2
class/class name 5 1 0 0 3 4
class/attribute name 5 5 1 1 1 2
class/attribute-role name 4 7 1 1 2 4
They can obtain more precision (with also more anal-
ysis work) with the class/attribute-role name lattice,
where 119 potential GCM concepts are proposed. We
are currently working to assist the expert in this anal-
ysis task (Osman Guedi et al., 2011). We can also de-
duce from these results that the two versions of pesti-
cide model are very close: there are only few specific
concepts.
7 RELATED WORK
FCA is used to improve the abstraction quality and
the duplication elimination in class models in various
domains (software engineering, ontology mapping or
merging). This feature led us to propose the construc-
tion of a GCM to capitalize the knowledge of various
domains.
Many variants have been studied, which take into
account different characteristics for classes (the en-
tities or domain-concepts in this framework): at-
tribute names, attribute types, operation names, oper-
ation signatures, type specialization. . . The relevance
of this approach is related to the properties satisfied
by the class model after refactoring: all duplications
are eliminated and the specialization relation between
formal concepts meets the inclusion of features in the
class model. These previous approaches only focus
on intra-model factorization. In this paper, we use
FCA for inter-model factorization, and we need to
analyze differently the lattices, to identify categories
of formal-concepts useful to build the greatest com-
mon model of several input class models. We define a
guide for the expert to assist the building of the GCM.
Indeed, in this work, we assume that if two charac-
teristics have the same name, then these two charac-
teristics are identical. Some work includes semantic
analysis (Falleri, 2009; Rouane et al., 2007).
In software engineering, FCA has been used to
build and maintain class hierarchies (Godin and Mili,
1993; Dao et al., 2006; Arévalo et al., 2006). In this
paper, our objective is different, we want to find com-
mon and specific parts between several models. The
management of similarities and differences between
models has been studied in the domain of model ver-
sioning (Altmanninger et al., 2009). The Smover tool
uses direct comparison between a model and its pre-
vious version to detect syntactic and semantic con-
flict (Altmanninger et al., 2010). In order to manage
model conflicts in a distributed development context,
the work presented in (Cicchetti et al., 2008) proposes
the use of a difference model to store differences be-
tween two versions of a same model (Cicchetti et al.,
2007). These methods allow to show differences be-
tween models, but they don’t aim to propose auto-
matic core-concept detection. In the approach de-
scribed in (Ohst et al., 2003), models and diagrams
are considered as syntax trees, which allows the au-
thors to design a difference operation between mod-
els. Compared to the domain of model versioning, we
aim to present the GCM in a normal (factorized) form.
This is why FCA is more suitable for our problem.
UsingFormalConceptAnalysistoExtractaGreatestCommonModel
35

Table 3: Result of our approach on the complete EIS-Pesticides model.
L
GCM
L
pGCM
L
nM1
L
nM2
L
M1
L
M2
class/class name 111 34 0 0 1 1
class/attribute name 43 39 0 0 1 2
class/attribute-role name 68 119 0 0 8 9
Formal concept analysis has been used to per-
form ontology mapping or merging, which is an is-
sue close to ours (Kalfoglou and Schorlemmer, 2005;
Bendaoud et al., 2008). The approach proposed by
(Stumme and Maedche, 2001) uses FCA and linguis-
tic analysis to merge ontologies in a semantic web
context. In order to align ontologies, there are ap-
proaches that use a similarity measure, based on FCA
(Formica, 2006) or on ontologies internal structure
and association rule mining (Tatsiopoulos and Boutsi-
nas, 2009). All these works aim to perform ontology
mapping, while we work to extract the mapping result
and to abstract new domain-concepts.
Since the early 80s, the database domain has stud-
ied the problem of schema integration and data match-
ing, particularly in the database integration context.
The aim of database integration context is to produce
the global schema of a collection of databases (Ba-
tini et al., 1986; Rahm and Bernstein, 2001; Shvaiko
and Euzenat, 2005). Producing such a global database
schema is an issue close to the extraction of a greatest
common model in the sense that the search for identi-
cal concepts in different schemas is a necessary step.
There are a lot of work dealing with this problematic
in the literature. Generally, integration is composed
of different steps: schema transformation, correspon-
dence investigation and schema integration. Our work
focuses on correspondence investigation and schema
integration (Parent and Spaccapietra, 1998). The inte-
grated schema includes the GCM and the specific part
of the initial schemas. There are two groups of solu-
tions to semi-automatically find matches : rule-based
solutions and learning-based solutions. Our approach
is similar to rule-based solutions: we search similarity
between several model elements based on their char-
acteristics (Doan and Halevy, 2005). Unlike these ap-
proaches, the use of FCA allows to choose with fi-
nesse the way to describe the characteristics that we
consider. In this article, we focus on the description
of classes by their name, attribute name or role name,
but FCA opens many other possibilities.
8 CONCLUSIONS
During domain modeling activity, several teams with
different scientific skills usually make different mod-
els of a same domain. Each specialized team models
the part of the domain model it is familiar with, and fi-
nally, a unique, consolidated domain model has to be
built. This model integration requires the identifica-
tion of the common domain-concepts that are present
in the various specialized models.
Our contribution in this paper is an approach to
assist the gathering task for several given class dia-
grams describing the domain. The proposed method-
ology is based on Formal Concept Analysis and the
analysis of the formal-concepts using a decision tree.
It allows the production of a Greatest Common Model
in a normal (factorized) form. Our approach pro-
poses two levels of confidence for candidate GCM
concepts: domain-concepts which certainly will be
in the GCM, and domain-concepts that have to be
precisely analyzed, validated and named by experts.
Moreover, the approach identifies specific-concepts
and proposes possible new concepts that factorize the
original models. We have validated the scalability
of our approach by applying it on two versions of
the EIS-Pesticides model, versions containing about
125 classes. The results of our approach were ana-
lyzed, validated and used by A. Miralles, co-author
of this paper, who has a dual expertise: computer
science and spraying application techniques of pes-
ticides (Miralles et al., 1994; Miralles and Polvêche,
1998; Miralles et al., 2011).
One of the major perspective to our work is to im-
prove the GCM through the use of Relational Con-
cept Analysis (RCA), which is an FCA extension that
will allow us to work more precisely on the relation-
ships (UML associations) between domain-concepts.
In our running example, the use of RCA would
enable factorizing the Rainfall Instrumentation and
the Groundwater Instrumentation associations with a
new association connecting the new domain-concept
cl_Device with the cl_MeasuringStation class. Simi-
larly, RCA would extract a new association between
the new cl_Data class and cl_MeasuringStation, fac-
torizing both RainFall Information and GroundWater
Information associations.
Another perspective is the use of natural language
processing techniques to improve the name-based de-
scription of elements (classes, attributes, roles, etc).
The knowledge of semantic relations like hyper-
onymy, synonymy, or homonymy between terms will
refine the analysis of domain-concepts.
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
36

REFERENCES
Altmanninger, K., Schwinger, W., and Kotsis, G. (2010).
Semantics for accurate conflict detection in smover:
Specification, detection and presentation by example.
International Journal of Enterprise Information Sys-
tems, 6(1):68–84.
Altmanninger, K., Seidl, M., and Wimmer, M. (2009). A
survey on model versioning approaches. International
Journal of Web Information Systems, 5(3):271–304.
Arévalo, G., Falleri, J.-R., Huchard, M., and Nebut, C.
(2006). Building abstractions in class models: For-
mal concept analysis in a model-driven approach. In
Model Driven Engineering Languages and Systems
(MoDELS), pages 513–527.
Batini, C., Lenzerini, M., and Navathe, S. B. (1986). A
comparative analysis of methodologies for database
schema integration. ACM Computer Survey, 18:323–
364.
Bendaoud, R., Napoli, A., and Toussaint, Y. (2008). Formal
Concept Analysis: A unified framework for building
and refining ontologies. In International Conference
on Knowledge Engineering and Knowledge Manage-
ment (EKAW), pages 156–171.
Birkhoff, G. (1940). Lattice theory. American Mathemati-
cal Society.
Cicchetti, A., Ruscio, D., and Pierantonio, A. (2008). Man-
aging model conflicts in distributed development. In
Model Driven Engineering Languages and Systems
(MoDELS), pages 311–325.
Cicchetti, A., Ruscio, D. D., and Pierantonio, A. (2007).
A metamodel independent approach to difference rep-
resentation. Journal of Object Technology, 6(9):165–
185.
Dao, M., Huchard, M., Hacene, M. R., Roume, C., and
Valtchev, P. (2006). Towards practical tools for mining
abstractions in uml models. In International Confer-
ence on Enterprise Information Systems: Databases
and Information Systems Integration (ICEIS 2006),
pages 276–283.
Doan, A. and Halevy, A. Y. (2005). Semantic integration
research in the database community: A brief survey.
AI Magazine, 26:83–94.
Falleri, J.-R. (2009). Contributions à l’IDM : reconstruc-
tion et alignement de modèles de classes. PhD thesis,
Université Montpellier 2.
Formica, A. (2006). Ontology-based concept similarity
in Formal Concept Analysis. Information Sciences,
176:2624–2641.
Ganter, B. and Wille, R. (1999). Formal Concept Analysis:
Mathematical Foundation. Springer-Verlag Berlin.
Godin, R. and Mili, H. (1993). Building and maintain-
ing analysis-level class hierarchies using galois lat-
tices. In Eighth annual conference on Object-Oriented
Programming Systems, Languages, and Applications
(OOPSLA), pages 394–410.
Kalfoglou, Y. and Schorlemmer, M. (2005). Ontology map-
ping: The state of the art. In Semantic Interoperability
and Integration.
Miralles, A., Gorretta, N., Miller, P. C., Walklate, P.,
Van Zuydam, R. P., Porskamp, H. A., Ganzelmeier,
H., Rietz, S., Ade, G., Balsari, P., Vannucci, D., and
Planas, S. (1994). Orchard sprayers : an european
program to compare testing methods. In International
symposium on fruit nut and vegetable production pro-
duction engineering, Valencia Zaragoza, ESP, 22-26
mars 1993, pages 117–122.
Miralles, A., Pinet, F., Carluer, N., Vernier, F., Bimonte, S.,
Lauvernet, C., and Gouy, V. (2011). EIS-Pesticide:
an information system for data and knowledge capi-
talization and analysis. In Euraqua-PEER Scientific
Conference, 26/10/2011 - 28/10/2011, page 1, Mont-
pellier, FRA.
Miralles, A. and Polvêche, V. (1998). Effects of the agro-
chemical products and adjuvants on spray quality and
drift potential. In 5th International Symposium on
Adjuvants for Agrochemicals - ISAA ’98, volume 1,
pages 426–432, Memphis (USA).
Ohst, D., Welle, M., and Kelter, U. (2003). Differences be-
tween versions of uml diagrams. SIGSOFT Software
Engineering Notes, 28:227–236.
Osman Guedi, A., Miralles, A., Huchard, M., and Nebut, C.
(2011). Analyse de l’évolution d’un modèle : vers une
méthode basée sur l’analyse formelle de concepts. In
XXIXème Congrès INFORSID.
Parent, C. and Spaccapietra, S. (1998). Issues and ap-
proaches of database integration. Communication of
the ACM, 41:166–178.
Pinet, F., Miralles, A., Bimonte, S., Vernier, F., Carluer,
N., Gouy, V., and Bernard, S. (2010). The use of
uml to design agricultural data warehouses. In In-
ternational Conference on Agricultural Engineering
(AgEng 2010), pages 1–10.
Rahm, E. and Bernstein, P. A. (2001). A survey of ap-
proaches to automatic schema matching. The VLDB
Journal, 10:334–350.
Rouane, M. H., Dao, M., Huchard, M., and Valtchev, P.
(2007). Aspects de la réinginierie des modèles uml
par analyse de données relationnelles. Ingénierie des
Systèmes d’information (RSTI série), 12:39–68.
Shvaiko, P. and Euzenat, J. (2005). A Survey of Schema-
Based Matching Approaches Journal on Data Seman-
tics IV. In Spaccapietra, S. and Spaccapietra, S., ed-
itors, Journal on Data Semantics IV, volume 3730 of
Lecture Notes in Computer Science, chapter 5, pages
146–171. Springer Berlin / Heidelberg, Berlin, Hei-
delberg.
Stumme, G. and Maedche, A. (2001). Ontology merging
for federated ontologies on the semantic web. In In-
ternational Workshop for Foundations of Models for
Information Integration (FMII-2001), pages 413–418.
Tatsiopoulos, C. and Boutsinas, B. (2009). Ontology map-
ping based on association rule mining. In Inter-
national Conference on Enterprise Information Sys-
tems: Databases and Information Systems Integration
(ICEIS 2009), pages 33–40.
UsingFormalConceptAnalysistoExtractaGreatestCommonModel
37
