
Bayesian Networks for Matcher Composition in Automatic Schema
Matching
Daniel Nikovski
1
, Alan Esenther
1
, Xiang Ye
1
, Mitsuteru Shiba
2
and Shigenobu Takayama
2
1
Mitsubishi Electric Research Laboratories, 201 Broadway, Cambridge, MA 02139, U.S.A.
2
Mitsubishi Electric Corporation, 5-1-1 Ofuna, Kamakura, Kanagawa 247-8501, Japan
Keywords:
Data Integration, Virtual Databases, Uncertain Schema Matching.
Abstract:
We propose a method for accurate combining of evidence supplied by multiple individual matchers regarding
whether two data schema elements match (refer to the same object or concept), or not, in the field of automatic
schema matching. The method uses a Bayesian network to model correctly the statistical correlations between
the similarity values produced by individual matchers that use the same or similar information, in order to
avoid overconfidence in match probability estimates and improve the accuracy of matching. Experimental
results under several testing protocols suggest that the matching accuracy of the Bayesian composite matcher
can significantly exceed that of the individual component matchers.
1 INTRODUCTION
The problem of automatic schema matching (ASM)
between two or more database schemas arises in
many applications, such as data migration, when one
database has to be incorporated into another, virtual
databases, where a single interface is used to access
multiple databases, and data analysis, when multiple
databases are stored in a data warehouse with a single
schema. When two database schemas that describe
the same problem domain are given (e.g. purchase
orders, real-estate listings, books, etc.), the objec-
tive of an automatic schema matching (ASM) method
is to discover which pairs of elements from the two
schemas are likely to match, that is, likely to refer to
the same entity (e.g. shipping address, house price,
book title, etc.), and possibly to also estimate the con-
fidence of such a match.
The ASM problem is usually very difficult,
because when database designers create database
schemas, they rarely provide full and unambiguous
information about what individual schema elements
represent. Even if any such information exists, it is
usually not meant for computer processing. Rather,
database designers usually choose suitable words or
abbreviations for the names of data elements, so as to
facilitate future maintenance of the data schemas by
themselves or other humans. Because of this common
practice, lexical analysis of the names of data ele-
ments could be an effective approach to ASM. For ex-
ample, the names “Street”, “Str”, and “StreetName”
can be recognized to refer to a street, possibly in an
address, and lexical analysis by string matching can
reveal this similarity. A different type of information
that might be useful for ASM is the structure of the
data schemas, if present. In many cases, schemas are
not represented by a flat list of element names, but the
elements are organized in a hierarchy. For example,
the element “CustomerName” might have three sub-
elements, “FirstName”, “MiddleInitial”, and “Fami-
lyName”. Using such structural information is an-
other approach to ASM. Many more approaches exist:
for example, when the actual values of two database
fields come from the same statistical distribution (e.g.,
over names, numbers, etc.), this can serve as evidence
that the corresponding schema elements match. Dic-
tionaries, thesauri, and other auxiliary data sources
have been used for ASM purposes, too (Rahm and
Bernstein, 2001).
Due to the difficulty of the problem, no single
method has been shown to perform best on all ASM
tasks. This has led to the idea that multiple basic
matchers of the types described above can be used to-
gether in a composite matcher (Do and Rahm, 2002;
Tang and Li, 2006). The purpose of the composite
matcher is to combine the output of the individual
matchers and arrive at a more accurate set of likely
matches. In most cases, the output of an individual
matcher k for a given pair of elements S
1
.E
i
and S
2
.E
j
is a similarity value v
k
in the interval [0, 1], where
48
Nikovski D., Esenther A., Ye X., Shiba M. and Takayama S..
Bayesian Networks for Matcher Composition in Automatic Schema Matching.
DOI: 10.5220/0004001500480055
In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 48-55
ISBN: 978-989-8565-10-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

v
k
= 0 means no similarity, and v
k
= 1 means full con-
fidence that the two elements match. When given a
library of K different individual matchers, the objec-
tive, then, is to find a composite similarity measure v
that is a function of the individual outputs v
k
, k = 1, K.
Several methods for combining similarity values
have been proposed. The LSD system (Doan et al.,
2003) uses machine learning techniques to estimate
weighting coefficients w
k
such that the final similarity
measure v is a weighted average of the individual sim-
ilarity measures: v =
∑
K
k=1
w
k
v
k
. The COMA system
(Do and Rahm, 2002) extends this approach with the
minimum and maximum operators: v
min
= min
k
w
k
v
k
and v
max
= max
k
w
k
v
k
.
Although experimental results suggest that these
methods for combining similarity values lead to
matching accuracy that is higher than that of the ac-
curacy of the individual matchers, it can be recog-
nized that they are specific approaches to the funda-
mental problem of combining evidence from multi-
ple sources (in this case, multiple individual match-
ers), and make very specific assumptions about the
statistical structure of the evidence. These assump-
tions might or might not be warranted in practice. We
propose a general method for correct modeling of any
kind of statistical structure in the evidence, based on
Bayesian networks and probabilistic reasoning, and a
statistically grounded method for composing matcher
evidence using these Bayesian networks.
2 BAYESIAN NETWORKS FOR
COMBINING OUTPUTS OF
MULTIPLE SCHEMA
MATCHERS
When combining evidence from multiple sources, one
of the major problems and causes for errors is the im-
proper modeling of correlation and other forms of sta-
tistical dependence between variables in the problem
domain. For example, when two very similar match-
ers k and l are applied to an ASM problem, their out-
puts v
k
and v
l
will be highly correlated — when v
k
is
high, then v
l
will be high, too, and vice versa. For ex-
ample, a lexical matcher based on edit (Levenshtein)
distance would assign a medium-level similarity to
the pair of element names “Street” and “State”; simi-
larly, a lexical matcher based on the Jaccard distance
between the sets of letters in the two elements would
assign such similarity to the pair. For another pair of
elements, for example “Street” and “Address1”, both
lexical matchers would compute low similarity, be-
casue in this case similarity cannot be established on
the basis of string matching. In either case, not only
is the computed similarity misleading as regards to
the correct match, but both matchers provide the same
kind of evidence (both positive or both negative), so
its (in this case, harmful) influence is reinforced. If
a weighted sum of the two similarity values is used,
the same evidence will be counted twice, in practice,
which will result in a phenomenon known as over-
confidence. One of the matchers is almost redundant,
and including it in the composition process might ac-
tually decrease the accuracy of matching. This effect
has been observed in other fields where evidence has
to be combined, such as medical diagnosis, and one
possible tool for handling it has been belief reason-
ing in Bayesian networks. Our method for combining
matcher output is based on such a network.
2.1 Representation
A Bayesian network (BN) is a probabilistic graphical
model that represents a set of random variables and
their conditional dependencies by means of a directed
acyclic graph (DAG). An edge in the DAG between
two nodes signifies that the variable Y corresponding
to the child node is statistically conditionally depen-
dent on the variable X corresponding to the parent
node. This dependence is expressed in a conditional
probability table (CPT) stored in the child node for
Y . If X ∈ Par(Y ), where Par(Y ) is the set of par-
ent nodes of Y , this table contains probability entries
Pr(Y = y|Par(Y ) = z) for every possible combina-
tion of values x that X can take on and configurations
(sets of values) z that the variables in Par(X) can take
on. Likewise, when there is no direct edge between
two nodes, they are assumed to be conditionally inde-
pendent given their parents. In particular, when two
nodes have a common parent, but no edge between
them, they are assumed to be conditionally indepen-
dent given the value of their parent. The presence (or
absence) of edges in the DAG of a Bayesian network
is a way to express the statistical dependence (corre-
lation) between variables.
A Bayesian network to be used for combining out-
puts of individual matchers in an ASM task is shown
in Figure 1. Its DAG is a tree of depth four, with
some additional edges between some of the nodes.
The meaning of the nodes is as follows:
1. At the first (top) level, the root node corresponds
to a Boolean variable signifying whether two
schema elements match. This is the final hypoth-
esis that has to be evaluated.
2. The nodes at the second level of the trees repre-
sent independent ways in which the two element
BayesianNetworksforMatcherCompositioninAutomaticSchemaMatching
49

Overall Match
LM2
Lexical
Match
Structural
Matcher
Synonym
Matcher
Instance
Match
LM1
IM1
IM2
V
V
V V
V
V
1
2
3
4
5
6
Figure 1: A Bayesian network for combining the output of
multiple individual matchers.
names can match (lexical, structural, instance-
based, etc.). It is expected that these variables
are largely uncorrelated, because they use dif-
ferent information to test for possible matches.
They also each correspond to clusters of individ-
ual matchers whose output is correlated. In Fig-
ure 1, one cluster represents the hypothesis that
the two elements match lexically, and the other
cluster represents the hypothesis that the instances
(values) of the two elements in their respective
databases match.
3. The nodes at the third level of the tree are also
Boolean and represent the individual hypothesis
that the two elements match, according to a single
matcher. In Figure 1, these include two lexical
matchers LM1 and LM2, one structural matcher,
one synonym matcher, and two instance matchers
IM1 and IM2.
4. The leaves of the tree, at the fourth level, represent
the similarity values V
k
, k = 1,K of the individ-
ual matchers whose outputs have to be combined
(in this case, for the sake of illustration, K = 6).
These variables are continuous, and their possible
values are the real numbers v
k
.
The overall structure of the BN expresses the
understanding that when two elements match (or
don’t), the outputs of the structural matcher, syn-
onym matcher, the lexical match variable, and the
instance match variable will be statistically indepen-
dent. This is what is to be expected on a matching
task, because these matchers all use different infor-
mation from the two data schemas in order to com-
pute an estimate about whether the elements match.
However, the outputs of the two lexical matchers LM1
and LM2 would be correlated, as expected if they
use the same information (the names of the two el-
ements). That is why there exists an edge between
nodes LM1 and LM2. Similarly, the output of the
two instance matchers would be correlated, too, be-
cause they would both use the same information to
base their estimates on (namely, the contents of the
two corresponding database fields). Accordingly, an
edge between nodes IM1 and IM2 reflects this depen-
dency. This structure of the BN, then, corresponds to
our understanding of which matchers produce highly
correlated outputs, and which ones are statistically in-
dependent.
2.2 Parameter Estimation
In addition to the graph of the BN, if the network is
to be used for inference, the parameters in its CPTs
have to be specified, too. This can be done by means
of labeled cases, where pairs e
l
= (S
1
.E
i
,S
2
E
j
) of el-
ements S
1
.E
i
and S
2
.E
j
, l = 1, ..., N have been run
through all K matchers, to produce the corresponding
similarity values v
l,k
, l = 1, .. ., N, k = 1, ...,K, and
the correct labeling for some or all of the remaining
Boolean variables has been supplied, too.
If labels for all Boolean variables have been sup-
plied, then the estimation of the probabilities in
the CPTs of the Boolean nodes could be reduced
to frequency counting. That is, the entry Pr(Y =
y|Par(Y ) = z) is equal to the ratio of the number of
cases when Y had a specific value y (either True or
False) and the parents Par(Y ) of Y were in configura-
tion z, and the number of times the parents of Y were
in configuration z (regardless of the value of Y ). For
the continuous nodes V
k
, a suitable parametric model
for the similarity values must be chosen. One possible
model is a normal (Gaussian) distribution with mean
µand variance σ
2
. Then, two separate normal distri-
butions N(µ
k,+
,σ
2
k,+
) and N(µ
k,−
,σ
2
k,−
) are estimated
for positive (matching) and negative (non-matching)
cases (pairs of elements), respectively. The mean µ
k,+
is the average of the similarity values v
k,i
of all data
cases where the parent node X
k
of V
k
has been labeled
with value True. The parameter σ
k,+
is the sampled
standard deviation of these cases. Analogously, the
parameters µ
k,−
and σ
k,−
are the sample mean and
standard deviation of v
k,i
over all cases when the par-
ent node X
k
has been labeled with the value False.
It is also possible to estimate the parameters in the
CPTs when only some of the nodes have been labeled.
A typical situation arises when a human designer has
provided feedback about whether the two elements
match (that is, has assigned a Boolean value to the
root node of the BN), but has not explained why they
match (that is, whether the match is lexical, instance-
based, structural, based on a dictionary, etc.) This sit-
uation is more challenging, but as long as the graph
of the network is known and fixed, it is still possible
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
50

to estimate the most likely values of the parameters in
its CPT. This problem is known as parameter learn-
ing with partially observed data in Bayesian networks,
and can be solved by means of gradient ascent in the
likelihood function or the Expectation Maximization
algorithm, among other methods (Heckerman, 2001;
Thiesson, 1995).
Assuming there is a data set Σ of N independent
training cases, the log-likelihood scoring function is
log L(Θ|Σ) =
1
N
M
∑
i=1
N
∑
l=1
log P(X
il
|Pa(X
i
), θ
i
),
where Σ denotes the training data set, Pa(X
i
) denotes
the parents of the node X
i
, i = 1, ..., M, and Θ is the
parameter vector Θ =
{
θ
1
, .. ., θ
M
}
.
However, we only have partial observations,
which means that there are several hidden nodes with
no labels. For each training case, one pair of ele-
ments S
1
.E
i
and S
2
.E
j
is run through all K individual
matchers to produce the corresponding similarity val-
ues v
i, j,k
, and a true label of two elements matching or
not for the root node OverallMatch is provided by the
human designer. With known structure and partial ob-
servation, we can use the EM (expectation maximiza-
tion) algorithm to find a locally optimal maximum-
likelihood estimate of the parameters (Murphy, 2003).
After learning parameters from a training data set,
each discrete node has a conditional probability ta-
ble (CPT) specifying the probability of each state of
the node given each possible combination of parents’
states.
2.3 Inference
Given the individual similarity values V
k
= v
k
, k =
1,K that have been reported by all individual match-
ers, and a full Bayesian network with CPTs estimated
from data, we can evaluate the probability that the two
elements match on the basis of all evidence, by means
of a standard computational process known as belief
updating. One possible method to perform belief up-
dating is to construct the join tree of the Bayesian net-
work, and use if for inference. This can be done by
means of a number of commercial or freely available
reasoning engines. The continuous variables V
k
, un-
der the chosen Gaussian parametrization, can be in-
corporated into the process of belief updating in the
form of virtual (uncertain) evidence (Pan et al., 2006).
To supply virtual evidence to a belief updating engine,
all that is needed is the likelihood ratio of the observed
values v
k
for the similarity value variables V
k
:
L(V
k
= v
k
|X
k
)
.
=
Pr(V
k
= v
k
|X
k
= T )
Pr(V
k
= v
k
|X
k
= F)
=
N(v
k
|µ
k,+
,σ
2
k,+
)
N(v
k
|µ
k,−
,σ
2
k,−
)
,
where N(v|µ,σ
2
) is the probability that measurement
v comes from normal distribution with mean µ and
variance σ
2
, and X
k
is the parent node of V
k
in the
BN.
After the process of belief updating concludes, all
Boolean nodes in the network will be assigned proba-
bility values according to the observed evidence (val-
ues) v
k
for the similarity value variables V
k
. The prob-
ability of the root node is the final estimate that the
two elements match, given the combined evidence of
the individual matchers.
3 EXPERIMENTAL RESULTS
In order to evaluate the match accuracy of any
matcher described below, we used five XML schemas
for purchase orders, CIDX, Excel, Noris, Paragon and
Apertum, kindly provided to us by the University of
Leipzig. The figure of merit for evaluation of the ac-
curacy of matching was the popular f-measure, de-
fined as the harmonic mean of precision and recall,
as used in the information retrieval community. If
the number of true matches identified by the match-
ing system as such (hits) is A, the number of true
matches not identified as such (misses) is B, and the
number of cases when two elements do not match,
but the matcher incorrectly declares a match (false
positives) is C, the f-measure F can be computed as
F = 2A/(2A + B +C).
We developed 13 basic schema matchers and eval-
uated the ability of the proposed Bayesian method to
combine their outputs so as to improve the accuracy of
matching. Of these, 11 were lexical matchers: Cosi-
neSimilarity, HammingDistance, JaroMeasure, Lev-
enshteinString, BigramDistance, TrigramDistance,
QuadgramDistance, PrefixName, SuffixName, Affix-
Name, SubstringDistance. One matcher, PathName,
was structural, comparing the entire paths of the two
elements in their respective XML schemas. The last
basic matcher was neither lexical nor structural: the
Synonym matcher declared a match if and only if the
two tested elements were found in a list of synonyms
relevant to the domain of purchase orders. Based on
their method of operation, the similarity values com-
puted by the 11 lexical matchers can be expected to
be highly correlated and statistically dependent; in
contrast, the synonym matcher could be expected to
produce output that is largely independent of the lexi-
cal matchers. Experimental evaluation of their pair-
wise dependence confirms this intuition: Figure 2
shows the pairwise correlation between all 13 pairs of
matchers, evaluated from all pairs of elements in all
ten pairs of schemas. Clearly, all 11 lexical matchers
BayesianNetworksforMatcherCompositioninAutomaticSchemaMatching
51
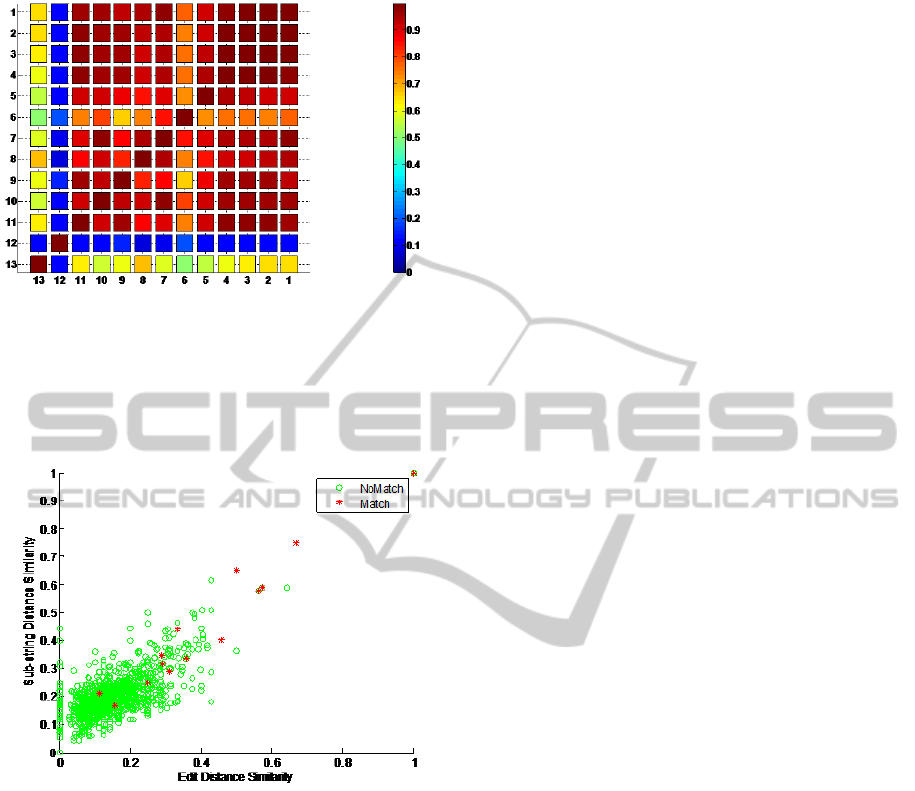
Figure 2: Pair-wise correlations between all pairs of basic
matchers, numbered as follows: 1: Edit Distance; 2: Sub-
string Distance; 3: Bi-Gram Distance; 4: Tri-Gram Dis-
tance; 5: Quad-Gram Distance; 6: Cosine Similarity; 7:
Hamming Distance; 8: Jaro Measure; 9: Affix Name; 10:
Prefix Name; 11: Suffix Name; 12: Path Name; 13: Syn-
onym.
Figure 3: Scatter plot of similarity values computed by the
Edit Distance (LevenshteinString) and SubstringDistance
matchers. Their output is clearly correlated, resulting in a
correlation coefficient of 0.9892.
are highly correlated, whereas their correlation with
the Synonym matcher is minimal. Somewhat surpris-
ingly, the structural matcher, PathName, is the least
correlated with any other matcher.
The kind of major correlation that exists between
lexical matchers is illustrated in Figure 3 that shows
a scatter plot of the similarity values computed by
the LevenshteinString (edit distance) matcher and the
SubstringDistance matcher. Their high correlation
(0.9892) makes one of them almost redundant, if the
other one is present.
Regarding the experimental evaluation of match-
ing accuracy, as with any machine learning method,
care should be given to the training and testing eval-
uation protocol, that is, which data are used for train-
ing and which data are used for testing. We used three
evaluation protocols, as described below.
3.1 Testing on Training Data set
This is the simplest evaluation protocol, where we
use the same data set for testing and training. Its
purpose is to evaluate how well we can fit the train-
ing data. Under this protocol, we define ten match-
ing tasks that correspond to all possible pairs of the
five XML schemas. For each matching task (pair of
schemas), we build a dedicated Bayesian composite
matcher that is specific for this task. The same data
set, then, is used as evidence to predict the belief for
every pair of elements. This is the most lenient eval-
uation protocol, since the learning algorithm has seen
during training the data that will be used for testing.
After a similarity matrix is computed for all pairs
of elements of two database schemas, an additional
global matching step called Max1/Delta is performed
to produce the final match decisions, based on the
understanding that most often (but not always) map-
pings between database elements are one-to-one (Do
and Rahm, 2002). Since this procedure is sensitive
to the exact value of the Delta parameter, we present
below results as a function of that paramater. After
global match decisions have been obtained, they are
compared with the ground truth, and the f-measure for
this pair of schemas is computed. These f-measures
are averaged over all pairs of tasks in the testing data
set (in this case, ten pairs of tasks), in order to arrive
at the final overall f-measure.
Figure 4 shows a comparison between all 13 ba-
sic matchers and the Bayesian Composite Matcher
(BCM). The accuracy of the BCM reaches 0.819 and
is significantly higher than that of any other matcher.
It is also practically constant for a wide range of the
parameter Delta. The performance of Path Name
matcher is better than other individual matchers, be-
cause it is a hybrid matcher combining two basic
match techniques.
3.2 Leave-One-Out Cross Validation
(LOOCV)
A more realistic testing protocol is under the leave-
one-out cross validation (LOOCV) method, where
training and testing data are clearly separated. Each
of the ten pairs of schemas is used for testing, using
a BCM that was learned using the other nine pairs of
schemas. The results are averaged over the ten pairs,
as follows:
1. Build training and testing data sets for 10 test
tasks. For instance, if the similarity matrix of
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
52
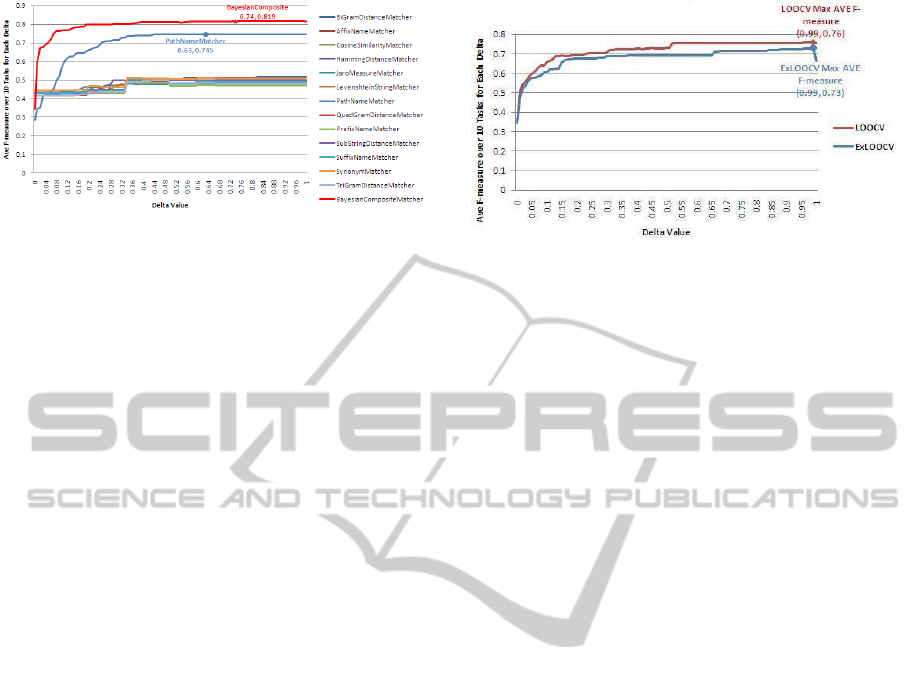
Figure 4: Comparison of average f-measure between the
Bayesian Composite Matcher and all other matchers.
Excel ↔ Noris is used as testing set, the training
data set for this test task is a collection of similar-
ity matrices of the remaining 9 schema pairs.
2. Learn one Bayesian composite matcher for each
task based on its training data.
3. Implement Max1/Delta selection approach on
the composite similarity matrix generated by each
Bayesian Composite Matcher.
3.3 Exclusive Leave-One-Out Cross
Validation (ExclLOOCV)
The second protocol described above still allowed
the training algorithm to see data from the pair of
schemas that would be used for testing, but not the
ground truth for their direct match. To eliminate any
exposure of the training algorithm to data that would
be used for testing, we modified the LOOCV pro-
cedure as follows. For each task, if the test pair is
A ↔ B, the training examples only come from the
three remaining schemas not involving either A nor B.
For example, if one test set is Excel ↔ Noris, it will
be tested with the Bayesian composite matcher that
has used only the following three pairs of schemas for
training: CIDX ↔ Apertum, CIDX ↔ Paragon, and
Apertum ↔ Paragon. This is the maximally realistic
testing protocol.
Figure 5 shows a comparison between the two
variants of the LOOCV evaluation protocol for the
Bayesian Composite Matcher. It can be seen that the
accuracy drops to 0.76 under usual LOOCV and 0.73
under exclusive LOOCV.
4 RELATED WORK
As mentioned in the first section, many methods for
creating composite matchers have been tried, and this
section explains the difference between them and the
proposed approach. One major distinction between
Figure 5: Comparison of Bayesian composite matcher per-
formance under LOOCV and exclusive LOOCV testing
protocols.
these methods is whether they rely on manual tun-
ing of the composition structure and parameters, or
such parameters are estimated from a training set and
verified on an independent test set. The composi-
tion methods developed in the COMA (Do and Rahm,
2002; Do and Rahm, 2007) and GLUE (Doan et al.,
2003) systems are based on manual tuning of the
composition parameters, so comparison with learning
methods for tuning parameters is not entirely correct;
a composite matcher that is manually tuned with a
specific set of schemas in mind can certainly be ex-
pected to be more accurate than a learning matcher
that is tested under a cross-validation protocol.
Among the learning methods for composing
matchers, our approach is most similar to the one pro-
posed by Marie and Gal (Marie and Gal, 2007), who
have approached the problem from a Bayesian net-
work perspective, too, arguing that a disciplined ap-
proach to handling match uncertainty has to be ap-
plied. However, their approach is based on Naive
Bayes networks, that is, two-level Bayesian networks
with one root node that corresponds to the matching
event, and many leaf nodes that are directly children
to the root node. It can be shown that such a Naive
Bayes network has the same classification properties
as a logistic regression model, and the decision sur-
face is linear, similar to the one used in the LSD and
GLUE systems (Doan et al., 2003; Doan et al., 2003).
In contrast, a full (non-naive) Bayesian network like
the one proposed in this paper can model arbitrary
correlations and decision surfaces.
Furthermore, the Bayesian network proposed in
this paper is also different from the Bayesian net-
work classifiers used in the YAM system (Duchateau
et al., 2009) in that our network includes unobserv-
able nodes corresponding to types of matchers; in
contrast, YAM employs the BayesNet classifier from
the WEKA library that can learn the structure of a
fully observable network by adding and removing
edges, but cannot add unobservable nodes (Witten and
BayesianNetworksforMatcherCompositioninAutomaticSchemaMatching
53

Frank, 2005). Unobservable nodes corresponding to a
type of matcher (e.g. lexical, dictionary-based, struc-
tural, etc.) present a natural way of representing the
conditional dependency between multiple matchers of
the same type, because they restrict the edges of the
graph only to the nodes of the same type. In contrast,
a fully-connected BN without hidden nodes would re-
quire an exponential number of CPT parameters to be
estimated, which would make it practically impossi-
ble to collect the data necessary for estimating them.
This problem is further compounded by the continu-
ous values of the similarity values produced by basic
matchers — in fact, it is not immediately clear how
YAM would have been able to learn a fully connected
BN with 13 continuous nodes representing the simi-
larity values of each basic matcher, from the few thou-
sand examples available from the PO dataset under
the two LOOCV protocols.
On the other hand, non-linear classifiers such as
decision trees (Duchateau et al., 2008) can indeed
represent non-linear decision surfaces from a lim-
ited number of training examples, but are not inher-
ently probabilistic, and the binary decisions output
by them are not easy to use in the global assign-
ment process that determines the entire mapping be-
tween two schemas from the pair-wise matches be-
tween their individual elements. Other probabilistic
approaches to the automatic schema matching prob-
lem include the use of an attribute dictionary in the
AUTOMATCH system, where training examples of
matching schemas are used to compile the dictionary,
and candidate elements from new schemas are com-
pared probabilistically to the dictionary. Although
this approach does result in probabilistic estimates of
matches, the compilation of the dictionary requires
many training examples, and is best suited to do-
mains where many pairs of entire schemas have to be
matched repeatedly.
5 CONCLUSIONS AND FUTURE
WORK
We have proposed a novel method for creating com-
posite matchers for the purpose of automatic schema
matching. Its main advantage is the explicit model-
ing of the conditional statistical dependence between
the similarity values computed by individual basic
matchers. Experiments suggest that it combines suc-
cessfully the outputs of such matchers, and achieves
matching accuracy significantly exceeding that of the
individual matchers. Furthermore, its outputs are es-
timates of the genuine probabilities of match, which
allows the application of decision-theoretic methods
for optimal judgment whether elements match, or not.
Further work will focus on leveraging the clear se-
mantics of the computed probabilities for improving
the accuracy of the global matching algorithm, as well
as on improving the computational properties of the
proposed Bayesian method.
REFERENCES
E. Rahm, P. A. Bernstein, A Survey of Approaches to Auto-
matic Schema Matching, VLDB Journal, 10:4 2001.
H. H. Do, E. Rahm, COMA - A System for Flexible Com-
bination of Schema Matching Approaches, in Pro-
ceedings of the 28th International Conference on Very
Large Data Bases (VLDB), 2002.
W. Li, C. Clifton, A Tool for Identifying Attribute Corre-
spondences in Heterogeneous Databases Using Neu-
ral Network, Journal of Data and Knowledge Engi-
neering 33: 1, 49-84, 2000.
A. Doan, P. Domingos, and A. Halevy., Learning to Match
the Schemas of Databases: A Multistrategy Approach,
Machine Learning Journal, no. 50, pp. 279–301, 2003.
S. Bergamaschi, S. Castano, M. Vincini, D. Beneventano,
Semantic Integration of Heterogeneous Information
Sources, Journal of Data and Knowledge Engineering
36: 3, 215-249, 2001.
H. H. Do, E. Rahm, Matching Large Schemas: Approaches
and Evaluation, Journal of Information Systems, Vol.
32, Issue 6, Sep. 2007.
A. H. Doan, P. Domingos, A. Halevy, Reconciling Schemas
of Disparate Data Sources: A Machine Learning Ap-
proach, SIGMOD 2001.
D. W. Embley, Multifaceted Exploitation of Metadata for
Attribute Match Discovery in Information Integration.
WIIW 2001.
D. Heckerman, A Tutorial on Learning Bayesian Networks,
Journal of Learning in Graphical Models, pp. 301-
354, 2001.
K. Murphy, An Introduction to Machine Learning and
Graphical Models, the Intel Workshop on Machine
Learning, Sep. 2003.
J. Tang, J. Z. Li, Using Bayesian Decision for Ontology
Mapping, Journal of Web Semantics, Vol. 4, Issue 4,
Dec. 2006.
Thiesson, B., Accelerated Quantification of Bayesian Net-
works with Incomplete Data, Proceedings of the Con-
ference on Knowledge Discovery in Data, 1995, pp.
306-311.
Rong Pan, Yun Peng, Zhongli Ding, Belief Update in
Bayesian Networks Using Uncertain Evidence, 18th
IEEE International Conference on Tools with Artifi-
cial Intelligence (ICTAI’06), 2006, pp.441-444.
A. Marie and A. Gal. Managing Uncertainty in Schema
Matcher Ensembles. Proceedings of the 1st Interna-
tional Conference on Scalable Uncertainty Manage-
ment. Washington, DC, October 2007, pp. 60-73.
A. H. Doan, J. Madhavan, R. Dhamankar, P. Domingos, A.
Halevy, Learning to Match Ontologies on the Seman-
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
54

tic Web, The VLDB Journal 12 (4), 2003, pp. 303-
319.
F. Duchateau, Z. Bellahsene and R. Coletta, A Flexible Ap-
proach for Planning Schema Matching Algorithms,
OTM Conferences (CooPIS), 2008, pp. 249-264.
F. Duchateau, R. Coletta, Z. Bellahsene, R. J. Miller,
Not Yet Another Matcher, Proceedings of CIKM’09,
Hong-Kong, China, November 2009, pp. 2079-2080.
Ian H. Witten, Eibe Frank, Data Mining: Practical Machine
Learning Tools and Techniques, Second Edition, Mor-
gan Kaufmann, 2005.
Berlin, J., A. Motro: Database Schema Matching Us-
ing Machine Learning with Feature Selection. CAiSE
2002, pp.452-466.
BayesianNetworksforMatcherCompositioninAutomaticSchemaMatching
55
