Development of Robust Learning Control and Application
to Motion Control
Meng-Shiun Tsai, Chung-Liang Yen and Hong-Tzong Yau
Department of Mechnaical Engineering and Advanced, Institute of Manufacturing with High-tech Innovations,
National Chung-Cheng Unviersity, 168, University Rd, MinHsiung, Chiayi, Taiwan
Keywords: Iterative Learning Control, Motion Control, Nurbs Curves, Robust H
∞ Control.
Abstract: In this paper, the error dynamic equation of the ILC algorithm is derived with consideration of parameter
uncertainties and noise. The H
∞
frame work is utilized using the derived error dynamics to design the robust
learning controller. The proper learning gain is designed based on an optimization process to ensure that
both tracking performance and convergence condition can be achieved. Simulation and experiments are
conducted to validate the robust learning algorithm and the system is stable ever under high payload
uncertainty.
1 INTRODUCTION
Iterative learning control (ILC) is a technique to
control the system when it operate same tasks
repetitively. The ILC can be applied to robot
manipulators (Tayabi and Islam, 2006), chemical
batch process (Lee and Lee, 2007), and so on. Many
schemes of the ILC including the 2D theory method
(Geng et al., 1990), stochastic method (Wang and
Afshar, 2009), inverse system (Ye and Wang, 2005),
and feedback learning operators (Goldsmith, 2002;
Chin et al., 2004) have been proposed. Technical
review on the methodologies and applications of the
ILC is referred to (Ahn et al., 2007).
System robustness is generally a major concern
in the implementation of ILC to either linear or
nonlinear systems. The adaptive iterative learning
control was proposed (French and Rogers, 2000).
The Lyapunov method was adopted to prove the
convergence of the algorithm. Other adaptive ILC
algorithms were proposed to handle system with
time-varying parameters using a positive-definite
Lyapunov-like sequence (Kuc et al., 1991). Another
approach to ensure system robustness is to utilize the
H
∞
theory to formulate the general design
framework for the ILC algorithm (Padieu and Su,
1990). In these papers, only the performance and
robustness analysis of ILC schemes are considered.
In this paper, two steps design process is
proposed. The first step is to design the H∞
controller without consideration of the system
uncertainty. But the noise effect is included in the
design process. The second step is to iterate the
learning gain such that the convergence condition is
satisfied even under large system uncertainty. The
learning gain served as the performance weighting
which is the loop optimization variable to further
minimize system performance. Simulations and
experiments are conducted to demonstrate the design
philosophy.
2 MODELLING OF SERVO
CONTROL SYSTEM
In this paper, the command-based ILC is applied to a
CNC milling machine tool (Tsai et al., 2006). The
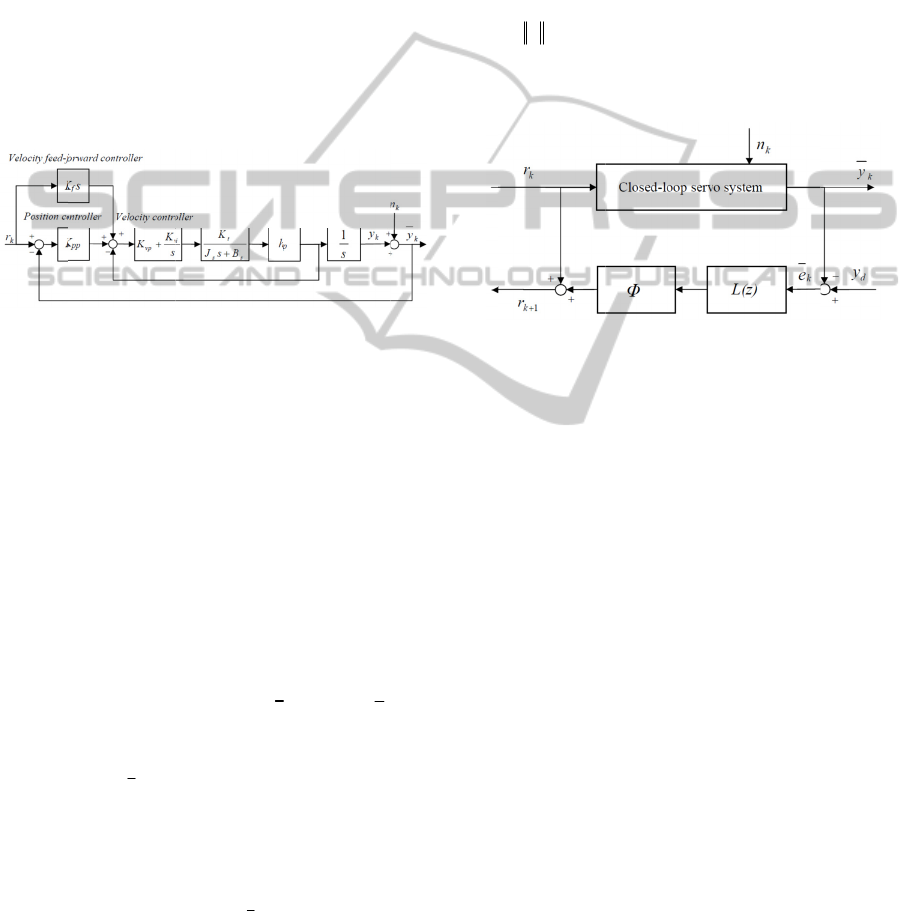
general servo control system as shown in Fig. 1
which includes the linear dynamic model of the
servo system, the velocity and position loops with a
velocity feedforward controller F(s). The function
)s(F
is designed as
sK
f
where
f
K
is the
feedforward gain. The J
s
, B
s
, K
t
and h
p
are the
moment of inertia, viscosity, torque constant and
pitch of lead screw. The parameters
vp
K
and
vi
K
in
the velocity loop can be designed by specifying the
damping ratio and bandwidth of the closed-loop
transfer function of the velocity loop. The position
gain
pp
K
in the position loop is determined by the
designed bandwidth of the position loop. The
148
Tsai M., Yen C. and Yau H..
Development of Robust Learning Control and Application to Motion Control.
DOI: 10.5220/0004008601480152
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 148-152
ISBN: 978-989-8565-21-1
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

feedfor
w
optimiz
a
the ma
g
various
f
function
s
referenc
e
)s(n
k
a
r
y
Bec
a
discrete
-
discrete
-
techniq
u
y
k
Figure 1
measure
m
3 O
P
In the
p
servo c
o
the erro
r
method
o
3.1
E
Figure
2
b
ased I
L
at the k
t
h
the des
i
denote t
h
the trac
k
tracking
L(z) an
d
comma
n
r
k+1
. Th
e
can be r
e
r
Afte
r
b
e simp
l
w
ard gain
K
a
tion approac
h
g
nitudes of
t
f
requencies.
A
s between
e
command
r
e givens as:
r)s(G)s(
y
k
rk
=
a
use the lear
n
-
time domain
-
time model
u
e and is give
n
r)z(G)z(
k
r
k
=
: Architectur
e
m
ent noise.
P
TIMIZA
T
p
revious sect
i
o
ntrol system
r
dynamics e
o
logy is propo
E
rror D
y
n
a
2
illustrates
t
L
C where r
k
a
n
h
and the (k+
1
i
red trajector
y
h
e measurem
e
k
ing error
w
error
k
e
p
r
o
d
learning ga
i
n
d
r
k
to obta
i
e
complete le
a
e
presented by
)
z(r)z(
r
k1k
=
+
y)z(e
dk
=
r
derivation,
t
l
ified as:
f
is design
e
h
, which min
i
t
he error tra
n
A
ccording to
F
the output
)s(r
k
, and
n)s(G)s(
k
n
k
+
n
ing process i
, E
q
. (1) is
using the
n
as:
n)z(G)z(
n
k
+
e
of servo c
o
T
ION PR
O
i
on, the gen
e
is develope
d
quation is d
e
sed.
a
mics Equ
a
t
he architect
u
n
d r
k+1
are th
e
1
)
th
iteration,
r
y
,
)z(n
k
,
y
e
nt noise, the
w
ith measure
m
o
cessed by a
i
n Φ is adde
d
i
n the new
u
a
rning proces
s
the followin
g
z(e)z(ΦL
)
k
+
)z(y)z(
k
−
t
he error dyn
a
e
d by usin
g
i
mizes the su
m
n
sfer functio
n
F
ig. 1, the tra
n
)s(y
k
and
the sensor
n
)s(
k
s implement
e
converted to
zero-order
h
)z(
k
o
ntrol system
O
CESS
ral model o
f
d
. In this sec
t
e
rived and d
e
a
tion
u
re of comm
a
e
input comm
a
r
espectively.
y
)z(
y
k
and
e
k
output signal
m
ent noise.
learning co
n
d
to the refer
e
u
pdated com
m
s
shown in F
i
g
equations.
)
a
mic equatio
n
g
an
m
of
n
at
n
sfer
the
n
oise
(1)
e
d in
the
h
old
(2)
with
f
the
t
ion,
e
sign
and-
a
nds
y
d
is
)z(
k
l
and
The
n
trol
e
nce
m
and
i
g. 2
(3)
(4)
n
can
p
er
f
fun
rep
r
the
W(
z
to
b
ex
p
k
e
Fig
u
me
a
3.
2
Af
t
ca
n
dy
n
for
m
dia
g
eq
u
b
y
t
wh
e
gai
n
opt
i
of
fun
out
p
Eq
u
fol
l
=
L
1k
(
1
e
=
+
Equation (
3
f
ormance is
s
ction
r
LG Φ .
U
r
esentation, t
h
nominal pla
n
z
) and given
a
G
r
(z)=
Here
△ (z) i
s
b
e 1 <
∞
Δ .
T
p
ressed as:
r
0
1
k
GΦL1[
−
=
+
u
re 2: Archit
a
surement nois
e
2
Robust
er developin
g
n
be designe
d
n
amics into a
l
m
(Zhou et a
l
g
ram corres
p
u
ation (12). T
h
t
he following
⎢
⎢
⎢
⎣
⎡
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
L
1k
J
W
0
0
y
e
y
Φ
Φ
e
re P
A
is the
n
which is
i
mization pro
the augmen
ction L(z), i
n
p
ut of the l
e
u
ation (6) c
a
l
owing form:
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
L
y
Z
~
The relation
b
L
(z)y
L
. The au
g
kr
Φ
e)ΦLG-
1
+
3
) indicates
s
trongly infl
u
U
sing the m
u
h
e G
r
can be
n
t G
r0
(z) and
t
s:
G
r0
(z)(1+W
(z
s
the small p
e
T
he errors dy
n
k
0
Φ
L
e])W(I
+
+
Δ
e
cture of co
m
e
.
ILC usin
g
g
the error dy
n
d
by first t
r
l
inear fractio
n
l
., 1996). Fig
u
p
onding to
h
e block diag
r
LFT form gi
v
−
0r0r
0r0r
0GG
II0
0GG
Φ
Φ
Φ
Φ
a
ugmented p
l
the design
c
ess, y
J
, y
L
, u
J
t
ed plant, i
n
n
put to the
e
arning funct
i
a
n be furthe
r
⎢
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
2221
1211
u
W
PP
PP
b
etween the
y
g
mented syst
e
kr
n
Φ
LG
that the
u
enced by th
e
u
ltiplicative u
n
further repre
s
t
he weightin
g
(
z) △ (z))
e
rturbation n
o
y
namics can
b
k
0r
n]WΔI[
Φ
LG +
m
man
d
-
b
ased
H ∞ Contr
o
n
amics, the
H
r
ansforming
n
transformat
i
ure 3 shows
the error
r
am can be re
p
v
en as:
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
L
k
k
J
A
L
k
k
J
u
e
n
u
P
u
e
n
u
I
l
ant,
Φ
is th
e
n
ed variable
J
and u
L
are
t
n
put to the
augmented
p
i
on L(z), res
p
e
r represente
d
⎥
⎥
⎦
⎤
L
u
W
~
y
L
and u
L
is g
i
e
m can be ex
p
(5)
tracking
e
transfer
n
certainty
s
ented by
g
function
(6)
o
rmalized
b
e further
k
(7)
ILC with
o
l
H
∞
control
t
he error
i
on (LFT)
t
he block
dynamic
p
resented
(8)
e
learning
for the
h
e output
learning
p
lant and
p
ectively.
d
by the
(9)
i
ven as u
L
p
ressed as
DevelopmentofRobustLearningControlandApplicationtoMotionControl
149

a stand
a
shown b
Figure 3
consideri
n
With th
e
p
erturbe
d
the robu
the tw
o
learning
and
W
~
c
T
It is no
t
design c
r
And
ILC alg
ensure t
h
Equ
a
should
b
conditio
n
3.3
O
By obse
r
found t
h
algorith
m
uncertai
n
p
rocess,
conside
r
follows.
a
rd form for
elow:
1k
J
e
y
z
~
=
⎥
⎦
⎤
⎢
⎣
⎡
=
+
2
1
L
Py =
: Architecture
n
g measureme
n
e
developed
m
d
system mo
u
st H
∞
control
o
Riccati eq
u
function L, t
c
an be repres
e
⎢
⎣
⎡
−
−
=
W
~
Z
~
LW
0
T
Φ
t
ed that the
f
r
iteria in sele
c
∞
W
~
Z
~
T
the sufficien
t
g
orithm (Roo
v
h
at
T
W
~
Z
~
a
tion (12) im
p
b
e set in or
d
n
.
O
ptimizati
o
r
ving the clo
s
h
at the stabilit
y
m
are str
o
n
ties. Before
the H
∞
cont
r
r
ing the pla
n
designing t
h
L1211
uPW
~
P +
=
L22
1
uPW
~
+
of ILC synt
h
n
t noise
m
odels by Eq
s
del can be u
s
ler can be de
s
u
ations. Af
t
e
he closed lo
o
e
nted as the f
o
−
−
0r
0r0r
LG
1LG
GG
Φ
Φ
ΦΦ
f
ollowing eq
u
c
ting the lear
n
∞
≥
0r
ΦG
t
convergenc
e
v
er, and Bo
s
1
W
~
≤
∞
p
lies that the
c
d
er to satisfy
o
n Process
s
ed loop tran
s
y
and perfor
m
o
ngly infl
u
introducing
r
oller designe
d
n
t uncertain
t
h
e H
∞
contro
h
esis problem
s
. (8) and (9)
,
s
ed for desig
n
s
igned by sol
v
e
r designing
o
p between t
h
o
llowing:
⎥
⎦
⎤
0r
G
u
ation provid
n
ing gain
Φ
.
e
condition o
f
s
gra, 2000) i
c
ondition of
Φ
the converg
e
s
fer function,
m
ances of the
enced by
the optimiz
a
d
process wit
h
t
ies is give
n
o
llers
(10)
(11)
with
, the
ning
ving
the
h
e
Z
~
(12)
d
es a
(13)
f
the
i
s to
(14)
1
Φ
<
e
nce
it is
ILC
the
a
tion
hout
n
as
wh
e
au
g
for
m
tra
n
fol
l
Fig
u
lea
r
lea
r
sat
i
ini
t
des
p
la
n
co
n
of
t
inc
l
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
L
1
y
Z
~
e
re
⎢
⎣
⎡
=
21
11
2A
P
P
P
g
mented syst
e
m
for H
2
/H
∞
c
k
L
e
y
z
~
⎢
⎣
⎡
=
With the d
e
n
sfer functi
o
l
owing:
[
1
1
W
~
Z
~
LG
PT
1
Φ =
=
u
re 4: The flo
w
r
ning controlle
r
The design
p
r
ning gain
Φ
i
sfied. The p
r
ial value of
Φ
ign the cont
r
n
t. The secon
n
troller L(z) s
h
t
he converge
n
l
uded.
⎢
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
2221
1211
u
W
~
PP
PP
⎥
⎦
⎤
22
12
P
P
is the
e
m can be e
x
c
ontroller desi
111
1
k
J
P
W
~
P
y
+=
⎥
⎦
⎤
+
signed contr
o
o
n can be
]
0r0r
2
2
12
1
1
LG1
G
LPI(P
Φ −
−+
w
chart of des
i
.
p
rocess is to
and ensure t
h
r
ocedure start
s
Φ
and then a
p
oller L(z)
b
a
s
d
step is to e
n
h
ould satisfy
t
n
ce where t
h
⎥
⎥
⎦
⎤
L
1
u
W
~
augmented
p
x
pressed as a
i
gn as shown
b
L12
u
P
o
ller, the cl
o
represented
]
21
1
2
LP)
−
igning learnin
g
start by sel
e
h
e stability c
o
t
s by first ch
o
a
pply the H
∞
s
ed on the a
u
n
sure that the
t
he sufficient
h
e plant unc
e
(15)
p
lant. The
standard
b
elow:
(16)
o
sed loop
as the
(17)
g
gain and
e
cting the
ndition is
o
osing an
theory to
u
gmented
designed
condition
e
rtainty is
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
150

4 E
X
To vali
d
and exp
machine
machine
MHMD
0
servo d
r
each ax
i
(RTX) (
V
control
output
d
the Ad
v
p
aramet
e
approac
h
a linear
s
1 Volt t
o
1000 H
z
Transfe
r
1999).
T
velocity
1.0 and
5
of positi
o
251.33
r
f
K
is s
e
To
e
applied
t
curve is
Fig.5. T
h
tested i
n
p
ayload
to devi
a
corresp
o
uncertai
n
After ap
p
is foun
d
range o
f
X
PERIM
E
d
ate the desi
g
eriments are
tool system
.
tool ar
0
42S1S serv
o
r
ives. The re
s
i
s is equal to
V
enturCom I
n
system with
d
ata from the
v
antech 178
4
e
rs are identi
f
h
. The nomin
a
s
wep
t
-freque
n
o
1 Volt and
t
z
, and ident
i
r
Function Es
t
T
he damping
r
close
d
-loop
t
5
02.65 rad/se
o
n closed-loo
r
ad/sec and
t
e
lected to 0.9
5
e
nsure that t
h
t
o a complex
used as a
w
h
ree payload
s
n
the moving
changes can
c
a
te about 8
%
o
nding weigh
t
n
ty bounds is
)s(W
=
Figure 5:
p
lying the de
s
d
that the lea
r
f
0.3 and 0.
5
E
NTAL V
A
g
n process, si
m
performed
u
.
The x, y,
a
e driven
o
motors an
d
s
olution of th
1μm. The r
e
n
c., 2006) is
u
real-time
p
linear scale
4
encoder
c
f
ied using a
f
a
l plant G
r0
(s)
n
cy signal at t
h
t
he frequenci
e
i
fied by usi
n
t
imate (ETF
E
r
atio and the
t
ransfer funct
i
c, respectivel
y
p transfer fu
n
t
he velocity
5
.
h
e proposed
a
trajectory, a
w
orking exa
m
s
given as 0,
1
platform. T
h
c
ause the mo
m
%
and 16%,
r
t
ing function
given as:
200s
s5.0
+
=
The butterfly c
s
ign process
s
r
ning gain
Φ
5
3 to satisfy
A
LIDATI
O
m
ulation ana
l
u
sing a three
-
a
nd z axes o
f
by Panas
d
MHMD04
2
e linear scal
e
e
al-time exte
n
u
sed to ensur
e
p
erformance.
are processe
d
c
ard. The
p
f
requency do
m
is measured
w
h
e magnitud
e
e
s from 0.1
H
n
g the Empi
r
E
) method (Lj
u
bandwidth o
f
i
on are chos
e
y
. The band
w
n
ction is chos
e
feedforward
a
lgorithm ca
n
b
utterfly NU
R
m
ple as show
n
1
0, and 20 K
g
h
e 10 and 2
0
m
ent of inert
i
r
espectively.
W(s) to cove
r
u
rve.
s
hown in Fig.
should be i
n
the converg
e
O
N
l
ysis
-
axis
f
the
s
onic
2
S1S
e
for
n
sion
e
the
The
d
by
p
lant
m
ain
with
e
of -
H
z to
r
ical
ung,
f
the
e
n as
w
idth
e
n as
gain
n
be
R
BS
w
n in
g
are
0
Kg
i
al J
s
The
r
the
(18)
4, it
n
the
e
nce
co
n
to
b
too
l
res
p
b
et
w
lea
r
an
d
the
the
val
u
co
n
we
i
99.
4
val
u
co
n
we
i
99.
3
ma
x
un
d
10
k
98.
Th
e
sat
i
out
p
loa
d
Fig
u
cas
e
n
dition. The
o
b
e 0.53.
Experiments
l
with the
p
a
y
p
ectively. T
h
w
een the c
a
r
ning after th
e
d
7. From the
r
x-axis and t
h
conditions
u
es of x-axi
s
n
ditions of t
h
i
ght and loa
d
4
0% and 99.
4
u
es of y-axi
s
n
ditions of t
h
i
ght and loa
d
3
0% and 9
9
x
imu
m
value
s
d
er the condit
i
k
g weight a
n
16%, 98.71
%
e
results illu
s
i
sfies the syst
e
p
ut tracking
d
ings.
u
re 6: The co
m
e
s of without le
o
ptimal learni
are conduct
y
loa
d
equal t
o
h
e comparis
o
a
ses of with
o
e
10th iteratio
r
esults, the tr
a
h
e y-axis are
of different
s
output trac
k
h
at without l
d
ing 20 kg
w
4
1% after 1
0
s
output trac
k
h
at without l
d
ing 20 kg
w
9
.12% after
s
of the x-axi
s
i
ons of that w
i
n
d loading
2
%
and 98.77
%
s
trate tha
t
n
o
e
m robustnes
s
errors are s
i
m
parisons of tr
a
a
rning and the
l
i
ng gain is d
e
t
ed on the
m
o 0, 10 kg a
n
o
ns of track
i
o
ut learning
o
n are shown
i
a
cking perfor
m
much impro
v
loadings.
T
k
ing errors
u
l
oading, load
i
w
eight reduce
0
iterations.
T
k
ing errors
u
l
oading, load
i
w
eight reduce
10th iterat
i
s
output track
i
w
ithout loadin
g
2
0 kg weig
h
%
after 10th
o
t only the
c
s
but also the
i
milar under
a
cking error b
e
learning.
e
termined
m
achining
n
d 20 kg,
i
ng error
and the
i
n Figs. 6
m
ances of
v
ed under
he RMS
u
nder the
i
ng 10kg
99.40%,
T
he RMS
u
nder the
i
ng 10kg
99.33%,
i
on. The
i
ng errors
g
, loading
h
t reduce
iteration.
c
ontrolle
r
trends of
different
e
tween the
DevelopmentofRobustLearningControlandApplicationtoMotionControl
151

Figure 7:
the tracki
n
5 C
O
A modi
f
this pap
e
choosin
g
learning
method
o
learning
Experi
m
with dif
f
reductio
n
iteration
s
compari
s
p
ayload
s
achieve
d
ACK
N
The aut
h
Affairs,
to this s
t
SE - 10
1
REF
E
Ahn, H.
S
learn
i
Tran
s
1121.
French,
M
learn
i
Inter
n
Geng, Z.
,
mode
The trends for
ng errors.
O
NCLUS
I
f
ied H
∞
opti
m
er
to provid
e
g
the learni
n
function.
o
logy, the a
p
function ca
n
m
ents are con
d
f
erent loading
n
of trackin
g
s for the no
m
s
ons betwee
n
s
demonstrate
d
.
N
OWLE
D
h
ors are grate
f
R. O. C. for
t
t
udy under co
n
1
, and 100-E
C
E
RENCES
S
., Chen, Y. Q.
i
ng control: bri
e
s
. on Systems,
M
., and Roge
r
i
ng by an
n
ational Journ
a
,
Carroll, R., a
n
e
l and algorit
h
the RMS and
m
I
ONS
m
ization proc
e
e
a systemati
c
n
g gain an
d
According
p
propriate le
n
be designe
d
d
ucted on th
e
conditions. I
t
g
error is o
v
m
inal plant.
n
the plant
s
that system
r
D
GEMEN
T
f
ul to the Min
i
t
he financial
s
n
tract 98 – E
C
C
-17-A-05-S1
-
, and Moore,
K
e
f survey and c
Man, and Cy
b
r
s, E., 2000,
adaptive Ly
a
a
l of Control, 7
3
nd
Xie, J., 199
0
h
m analysis fo
m
aximum valu
e
ss is propos
e
c
methodolog
d
designing
the prop
o
arning gain
d
simultaneo
u
e
machining
t
t
is shown tha
t
v
er 97% afte
r
Furthermore,
s
with diff
e
r
obustness ca
n
T
S
i
stry of Econ
o
s
upports prov
C
– 17 – A –
0
-
189, respecti
K
. L., 2007, Iter
ategorization,
I
b
ernetics, 37, 1
Nonlinear iter
a
punov techn
i
3
, 840-850.
0
, Two-dimens
i
r
a class of iter
a
u
es of
e
d in
g
y in
the
o
sed
and
u
sly.
t
ools
a
t the
r
10
the
e
rent
a
n be
o
mic
v
ided
05 –
i
vely.
r
ative
I
EEE
1
099-
r
ative
n
ique.
i
onal
a
tive
Ku
c
Lee
Lju
n
Pa
d
Ta
y
Tsa
i
Ve
n
Wa
n
Ye,
Zh
o
learning contr
o
c
, T. Y., Nam,
learning contr
o
Robot. Autom.
,
, J. H., and Le
e
applied to b
a
Engineering P
r
n
g, L., 1999,
User. Prentice
d
ieu, F., and S
control syste
m
Processing, 4,
y
abi, A, and Isl
a
control for ro
b
Control Engin
e
i
, M. S., Li
n
Development
control algo
disturbance, a
n
Syst. Technol.,
n
turCom Inc.,
Documentatio
n
n
g, H., and
Structure Con
t
in Stochastic
S
Trans. on Aut
o
Y. Q., and
inversion lear
n
1556.
o
u, K., Doyle,
J
Optimal Contr
o
o
l systems. Int.
J
K., and Lee,
o
l of robot m
a
,
7, 835–841.
e
, K. S., 2007,
t
ch processes:
r
actice, 15, 13
0
System Identi
f
Hall.
u
, R., 1990,
H
m
s, Int. J.
A
465–474.
a
m, S., 2006,
A
b
ot manipulato
e
ering Practic
e
n
, M. T., a
n
of comman
d
-
b
r
ithm with c
o
n
d noise effec
t
14, 511-518.
2006, Vent
u
n
. Cambridge.
A
fsha
r
, P., 2
0
t
roller Design
f
S
ystems Using
matic control,
5
Wang, D.
W
n
ing control la
w
J
. C., and Glo
v
o
l. New Jersey
,
J. Control, 52,
J. S., 1991,
A
a
nipulators. IE
E
Iterative learn
i
An overvie
w
0
6-1318.
fication: Theo
r
H
∞ approach t
A
daptive Con
t
A
daptive iterati
v
o
rs: Experimen
t
e
, 14, 843-851.
nd
Yau, H.
b
ased iterativ
e
o
nsideration o
ts. IEEE Tran
s
u
rCom RTX
009, ILC-Bas
for Output PD
g
LMI Techni
q
54, 760-773.
W
., 2005, Cle
a
w
. Automatica,
v
e
r
, K., 1996,
R
,
Prentice Hall
.
833-862.
A
n iterative
E
E Trans.
i
ng control
w
. Control
r
y for the
o
learning
t
r. Signal
v
e learning
t
al results.
T., 2006,
e
learning
f friction,
s
. Control
6.5 SDK
e
d Fixe
d
-
F
Shaping
q
ues. IEEE
a
n system
41, 1549–
R
obust and
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
152