Automated Design of Reconfigurable Manufacturing Systems

A Framework based on a Genetic Algorithm and Discrete System Simulation

J. Padayachee and G. Bright

Discipline of Mechanical Engineering, University of KwaZulu-Natal, King George V Avn, Durban, South Africa

Keywords: Reconfigurable Manufacturing Systems, Discrete System Simulation, Genetic Algorithms, Manufacturing

System Design.

Abstract: The concept of Reconfigurable Manufacturing Systems (RMSs) was formulated due to the global necessity

for production systems that are able to economically evolve according to changes in markets and products.

Technologies and design methods are under development to enable RMSs to exhibit transformable system

layouts, reconfigurable processes, cells and machines. Existing manufacturing design systems do not

encapsulate concepts of reconfigurability in design mechanisms to obtain optimal RMS configurations. This

paper presents a framework for a resource allocation and shop floor design system within the context of

RMSs. The framework focuses on the automated generation of shop floor configurations for systems with

high product variety and shared resources. The DEVS, (Discrete Event System Specification), formalism is

used to model reconfigurable equipment and simulate manufacturing processes. The “design engine” in the

proposed framework, implements a genetic algorithm for the assembly, evaluation and optimisation of

candidate shop floor configurations and their corresponding DEVS models.

1 INTRODUCTION

The concept of Reconfigurable Manufacturing was

first proposed and formalised by researchers at the

University of Michigan in the late 1990s. A

definition of Reconfigurable Manufacturing Systems

as follows (Koren et al., 1999): “ A Reconfigurable

Manufacturing System (RMS) is designed at the

outset for rapid change in structure, as well as in

hardware and software components, in order to

quickly adjust production capacity and functionality

within a part family in response to sudden changes

in market or regulatory requirements.”

The RMS concept has evolved out of the

inadequacy of previous manufacturing paradigms in

addressing the global manufacturing challenges of:

economically managing the rapid rate of product

development, frequent changes in parts and

products, fluctuations in product demand and mix

and changes in product and process technology

(Malhotra et al., 2009). In order to address these

challenges RMSs are envisioned to exhibit

transformable system layouts, reconfigurable

processes, cells and machines. Reconfigurability in

RMSs is also specified to be achieved by the use of

modular mechanical hardware and control elements

that can be rapidly integrated into Reconfigurable

Machine Tools (RMTs), material handling systems,

quality control systems and product assembly

mechanisms to achieve new levels of system

functionality (Moon and Kota, 2002, Mehrabi et al.,

2000).

The nature of RMSs presents the necessity to

quickly alter factory floor configurations when the

system can no longer meet the demands of the

production schedule. The generation of RMS

configurations that facilitate alterations to its

machines is essential to maintaining system

productivity under changing production demands.

Existing manufacturing design systems do not

encapsulate concepts of reconfigurability in design

mechanism to obtain optimal RMS configurations.

This paper presents a framework for an automated

resource allocation and shop floor design system for

RMSs.

2 RELEVANT LITRATURE

A method for the design of a RMS was presented by

(Koren and Shpitalni, 2010). The method extends to

the design of a RMS configuration for a single part

153

Padayachee J. and Bright G..

Automated Design of Reconﬁgurable Manufacturing Systems - A Framework based on a Genetic Algorithm and Discrete System Simulation.

DOI: 10.5220/0004009001530158

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 153-158

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

family. The first stage in the method is a calculation

of the number of machines required to complete an

operation. The number of machines N, may be

arranged in a variety of different configurations. The

minimum number of stages in a configuration is

limited to the number of machine setups required to

produce the part family. Koren’s method requires

the manual population of a space of potential

configurations. The selection of an optimal

configuration then proceeds by eliminating those

configurations that cannot meet the required

production rate. Consideration is also given to

system throughput with machine reliability less than

100%, investment cost, scalability and floor space.

Koren and Shpitalni presented a manual method of

enumerating and evaluating candidate RMS

configurations. The number of configurations that N

machines may assume, grows factorially with the

number N. This method therefore requires

substantial amounts of time and human effort to

enumerate and evaluate different configurations.

The use of the Analytic Hierarchy Process,

(AHP), was proposed by (Abdi, 2005) for the design

of a suitable RMS. The AHP was originally

developed by Thomas L. Saaty and the details of this

algorithm may be found in (Saaty, 2008). The AHP

requires a set of design alternatives and a set of

design criteria as inputs to the algorithm. Abdi listed

reconfigurability, cost, quality and reliability as the

design objectives. The implementation presented by

Abdi required the manual enumeration of possible

RMS design configurations. This method, like

(Koren and Shpitalni, 2010), is unappealing due to

the time required to enumerate and rank various

configurations.

The use of a Genetic Algorithm to design a

Multiple Part Line (MPL) for RMSs was proposed

by (Tang et al., 2003). Tang defined a MPL as a line

that consists of several serial stages with a finite size

buffer between every two stages. Each stage consists

of identical machines in parallel that perform the

same set of tasks. The problem formulation

restricted the MPL to the production of a given part

family. It was assumed that the number of stages in

the MPL is predetermined by the designer and each

Figure 1: Illustration of a Parallel MPL (Tang et al., 2003).

part visits every stage in the MPL. The objective of

the optimisation was therefore, to allocate machines

to the various stages of the MPL from a given

library of available machines. Limitations in this GA

implementation include the specification that the

RMS layout assumed a form as depicted in Figure 1.

3 PARALLEL DEVS

SIMULATION

The use of computer simulation for the design of

RMSs has been largely overlooked. This research

pursues the use of simulation for manufacturing

system design within an automated framework. The

Parallel Discrete Event System (Parallel DEVS)

specification has been chosen as the formalism for

the simulator. DEVS was selected because the

formalism is hybrid, i.e capable of modelling both

discrete event and discrete time systems. The

formalism is also modular and hierarchical thus

making it suitable for creating manufacturing system

models that can be generated and modified

automatically during the execution of a genetic

algorithm. The Parallel DEVS variation of the

original DEVS formalism was introduced (Chow

and Zeigler, 1994). A Parallel DEVS model consists

of Atomic Models that are networked to form

coupled models. An Atomic DEVS model M is an 8-

tuple defined by:

 



   



 







  



Where:

X: is a set of input events;

Y: is a set of output events;

S: is a set of sequential states;

ext

: Q × X

→ S, is an external transition function;

where Q = {(s,te)|s



S, 0≤te≤ta(s)} is the total state

set of M and te is the time elapsed since the last the

last event;

int

: S → S, an internal transition function;

con

: S × X

→ S, is the confluent transition function;

λ: S → Y

, is an output function;

ta: S → Real, is the time advance function.

Atomic DEVS models have been used to model the

elementary components of a manufacturing system

such as buffers, machines, assembly stations, human

labourers, robots and material transport systems.

Atomic models are stored in a manufacturing

resource/ equipment library:

 







 





Atomic models from this library are selected to

create candidate design solutions for a

ICINCO 2012 - 9th International Conference on Informatics in Control, Automation and Robotics

154

reconfigurable manufacturing system. A candidate

design solution is a network of atomic models,

which, as a whole is a discrete system model of a

manufacturing system. The structure of a coupled

model according to the Parallel DEVS formalism is:

 



  



















 







Where:

X: is a set of input events;

Y: is a set of output events;

D: is a set if component names {i};

}: is a set of atomic components, {M

}



}: I

is the set of other atomic models, by name,

that influence the

atomic model

i,j

is the of set of input and output couplings

The structured population of the 6-tuple coupled

model to create viable candidate manufacturing

system configurations requires the use of a

reconfigurable process plan used in conjunction with

a selection and organisation strategy.

4 RECONFIGURABLE PROCESS

PLANS

A Reconfigurable Process Plan, unlike a traditional

process plan, is a set of all possible mappings

between a part feature and the variety of machines

that are available to create that feature. The most

elementary building block of a reconfigurable

process plan is a process descriptor. A process

descriptor P

j,k

is used to represent information

pertaining to the creation of feature k on a part, using

machine i in configuration (setup) j. Recall that the

machines available to RMSs are reconfigurable, this

is discussed in (Moon and Kota, 2002, Padayachee

et al., 2009). The description P

i,j,k

is a 3 – tuple

defined by:









  



where:

tm: is the time for part feature k to be completed on

machine i in configuration j;

q: is the feature quality confidence on machine i in

configuration j (0< q < 1);

c: is the cost of machining feature k on machine i in

configuration j.

The process descriptor therefore assists

automated resource allocation by presenting a

mapping between a part feature and a machine, as

well as the information that may be used to evaluate

the optimality of the relationship.

RMSs will contain multiple types of

reconfigurable machinery capable of providing

similar processing operations. Therefore the creation

of a feature on a part may be achieved by a variety

of machines with different setups; the number of

possibilities may be encapsulated in a set:





 





The set of feature may then be grouped to represent

an entire part; this may be written as an ordered set,

where the precedence of feature creation is

according to a prescribed sequence:











































Parts may also be grouped into part families, and

part families into product platforms (a family of

assemblies) as described above. The set

PLATFORM

is a set of all possible process plans

and corresponding resource allocations for a product

platform.

5 CANDIDATE RMS

CONFIGURATIONS

Candidate RMS configurations are generated by first

selecting a process descriptor for each part feature

. Once a process descriptor has been selected for

the creation of a part feature, the corresponding

machine is selected from the set LIB. The allocation

(final mapping) of machines to part features is stored

in a set called MAP. One MAP exists per part family.

This process is performed repeatedly until all

features on all parts to be manufactured have had a

manufacturing resource allocated to them. A flow

chart of the procedure is illustrated in Figure 2.

Multiple part features, on parts from the same

family, may be created by the same type of machine

(possibly with the same setup). Such features are

grouped into Operational Groups (OG). The

machines on which an OG is executed are grouped

for further analysis:

={<P

ijk

>,… }

In an OG, the feature number k and the setup

(configuration) number j of the process descriptors

change but the machine number i stays the same.

The elements of an OG are further divided to form

smaller Operational Clusters (OC), i.e.   .

Formation of operational clusters depends on

features requiring the same type of setup on the

same type of machine. Because RMSs allow

dynamic changes to machines and setups,

Automated Design of Reconfigurable Manufacturing Systems - A Framework based on a Genetic Algorithm and Discrete

System Simulation

155

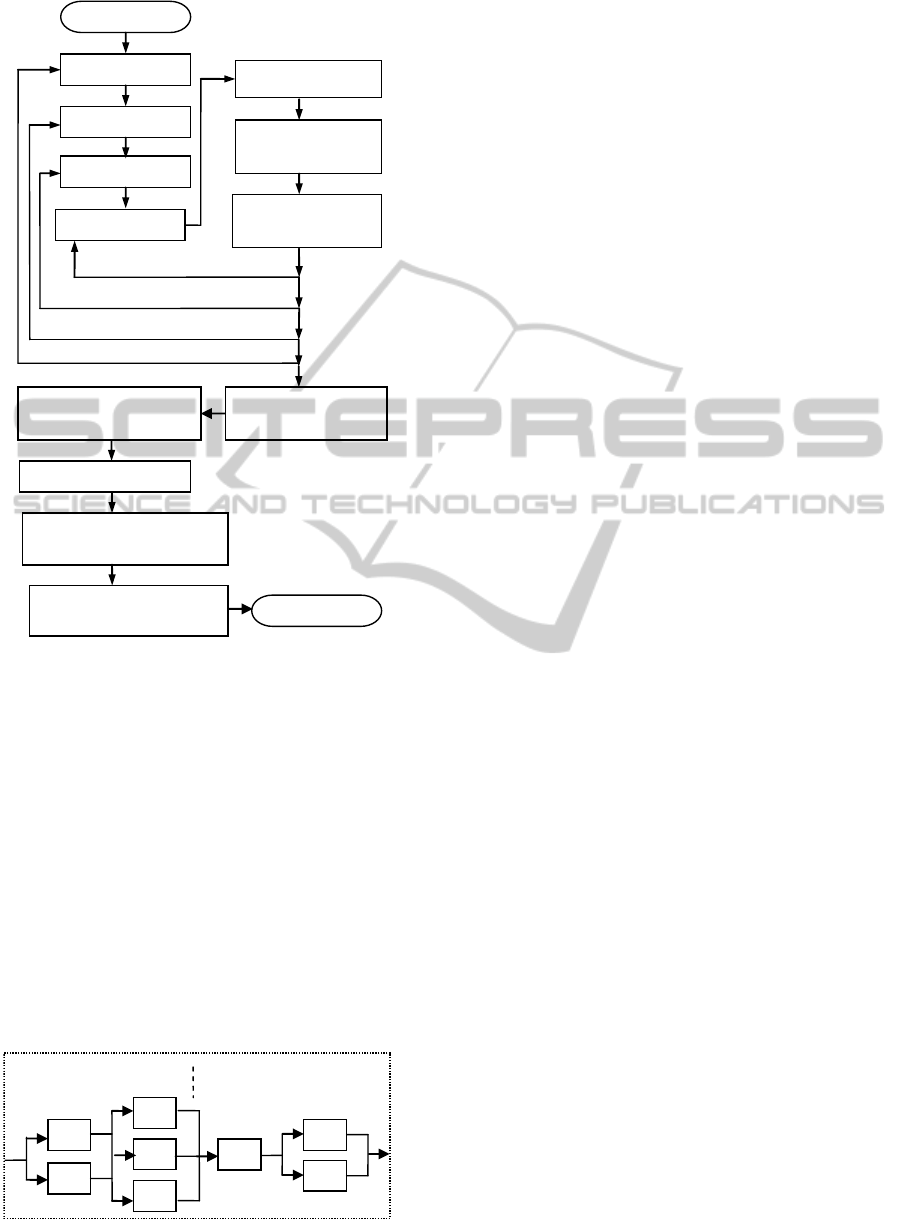
Figure 2: Process for Generating Candidate RMSs.

operational clusters may also be allowed on a

machine where the required setup change is minimal

between parts.

Machines in an OC are then duplicated until the set

of machines forms a STAGE able to provide the

required daily production rate. Multiple stages are

then spatially arranged according to a prescribed

sequence of operation:

= {STAGE

, …STAGE

}

The Spatial Configuration of stages (SC) will

correspond to one part family and its block of

manufacturing lines. The block of manufacturing

lines that are described by SC may be translated in to

facility layout diagrams as illustrated by Figure 3.

Figure 3: Spatial Configuration of a Block of Lines.

Multiple blocks of manufacturing lines such as those

illustrated in Figure 3 will be placed on the factory

floor for each part family in the system. All lines

will eventually lead to assembly stations. Facility

layout for assembly lines constitutes future work and

is not considered in this paper.

6 OPTIMISATION STRATEGIES

6.1 Feature – Machine Mapping

The design of a RMS may be optimised at multiple

levels using various modifications. The first

modification that can be made to the design is

changing the mapping between a part feature and the

machine used to make it. This will require the

complete redesign of the entire block of lines in

which that feature is created. Changing the machines

used to create a feature would usually require

swapping machines between other blocks of lines,

unless the library of manufacturing equipment has

excess machines of an appropriate type available

(practically unlikely). A single modification of this

type therefore has the ability to cause great changes

in a candidate solution. This type of modification is

therefore unsuitable as an optimisation mechanism.

A rule, algorithm (e.g. the Analytic Hierarchical

Process) or heuristic should be used for selecting the

most appropriate machine to create a feature at the

outset and once a mapping has been established it

should not be altered as an optimisation mechanism.

6.2 Operational Clusters, Stages and

Blocks

The division of operational groups into clusters, the

formation of stages from clusters and the

arrangement of stages into blocks of manufacturing

lines, is sizeable combinatorial optimisation

problem. The operational group will need to be

divided across multiple stages such that:

 the production rate under a static

production schedule is optimal,

 flow is balanced between different stages,

 the production rate is least diminished

when reconfigurations are required as per a

dynamically changing production schedule.

Finding an optimal configuration for a block of

lines, and considering that a manufacturing system

would consist of multiple blocks; the colossal task of

finding an optimal configuration for all blocks

would be a process that is best automated by a

SelectFEATURE

Select P

ijk

Select Corresponding

from LIB

Add mapping to set

MAP={<P

ijk

>,…}

Select FAMILY

Select PART

Select PLATFORM

for F

…

for PART

…

for FAMILY

…

for PLATFORM

…

Start

Candidate RMS

Spatial Configuration SC

Select Mat Handling and Buffers

from LIB, add to SC

Create OG from MAP

÷ OG to form smaller OC

Add all M

from SC to DN,

Populate< X, Y, D,{I

}, {Z

i,j

Duplicate M

in each stage

according to req Prod Rate

OC1.1

OC1.2

OC2.2

OC2.1

OC1.2

OG 1

OG 2

Stage 1

Stage 5

ICINCO 2012 - 9th International Conference on Informatics in Control, Automation and Robotics

156

suitable algorithm.

7 OPTIMISATION ROUTINE

7.1 Genetic Encoding

As a first initiative in the development of an

automated design system for RMSs, the authors

propose that the optimisation of the design be

executed within the structure of a Genetic

Algorithm. Encoding for an operational group and

its corresponding operational clusters is a binary

matrix of links between machines and features:

 

 

  























Each row of the matrix represents machines from 1-

n and each column, the features that could be created

on those machines from 1-k. Blocks of operational

group lines are stored in the ordered set BLOCK.

 







  





7.2 Genetic Operations

Standard genetic operations are gene mutation and

crossover. For gene mutation pair wise “bit flipping”

of elements in an operational group matrix is

performed. The operation is pair wise because once

a feature has been assigned a new operational cluster

within a group, its assignment to another cluster

must be deactivated.

For genetic crossover to be performed in a

meaningful way, while still maintaining the integrity

of a candidate solution, this operation has been

restricted to swopping of ‘OG’ elements from one

BLOCK set with those from another BLOCK for the

same part family.

7.3 Execution of Algorithm

The execution of the Genetic Algorithm begins with

the creation of an initial set of candidate solutions as

per the routine outlined in Section 5. When an initial

set of candidate solutions have been created the

encoding of the solution must be represented in two

formats; a format that may be used to construct

DEVS models and a genetic encoding. DEVS

coupled models are assembled and simulated to

produce results that may be analysed and used for

fitness evaluations. The use of simulation as part of

the optimisation procedure is essential for examining

the effect that reconfiguration will have on the

production rate for different OG and BLOCK

configurations. Simulation will also help identify

zones of buffer over flow, buffer starvation and

unacceptable machine idle times and idle

frequencies. Data analysis of simulation results

therefore has the ability to be used to exactly exploit

problematic areas by means of genetic operators.

However, a balance between solution exploitation

and exploration must be observed to prevent

premature convergence of solutions onto local

minima.

Figure 4: Execution Cycle for Genetic Algorithm.

A performance metric for a block of lines would

be the ratio of reconfiguration sensitivity to cost.

Reconfiguration sensitivity is an indicator of the

effect of reconfigurations on the productivity of a

block of lines. A suitable formulation and method of

determining reconfiguration sensitivity constitutes

future work.

Once candidates have been selected for genetic

operations and these operations have been applied to

create modified solutions; the genetic encoding must

be translated into new DEVS models for the next

iterative cycle. This cycle is shown in Figure 4, and

continues until no significant improvement is

demonstrated between successive iterations.

8 CONCLUSIONS

The framework presented in this paper requires

significant software development for the full

automation of the design system. A major

component of future work will include the software

development of the automated RMS configuration

generator and DEVS model assembler. The software

implementation will be built on the modeling

formalism presented in Section 3, the concept of

reconfigurable process plans presented in Section 4

and the routine presented in Section 5.

The exploration of appropriate Genetic

Candidate RMSs

DEVS Simulation

Data Analysis &

Fitness Evaluation

Genetic Operations

Assemble DEVS

coupled models

Translate Genetic

encoding to DEVS

Automated Design of Reconfigurable Manufacturing Systems - A Framework based on a Genetic Algorithm and Discrete

System Simulation

157

Algorithm configurations will also be conducted.

This will include research into advanced

performance metrics, improves genetic

recombination techniques and offspring selection

strategies. This research is necessary to ensure the

implementation of an algorithm that does not

converge prematurely on to sub-optimal RMS

configurations.

ACKNOWLEDGEMENTS

The authors would like to gratefully thank the

Technology Innovation agency, (TIA), together with

the Department of Science and Technology- South

Africa for the provision of project funding and

resources during this research.

REFERENCES

Abdi, M. R. 2005. Selection of a Layout Configuration for

Reconfigurable Manufacturing Systems using the

AHP. 8th International Symposium on the Analytic

Hierarchy Process Multi-criteria Decision Making.

Honolulu, Hawaii, USA.

Chow, A. C. H. & Zeigler, B. P. 1994. Parallel DEVS: A

Parallel Hierarchical, Modular Modeling Formalism.

In: Proceedings of 1994 Winter Simulation

Conference, Lake Buena Vista, FL, USA.

Koren, Y., Heisel, U., Jovane, F., Moriwaki, T.,

Pritschow, G., Ulsoy, G. & Van Brussel, H. 1999.

Reconfigurable Manufacturing Systems. Annals of the

CIRP, 48, 527-540.

Koren, Y. & Shpitalni, M. 2010. Design of Reconfigurable

Manufacturing Systems. Journal of Manufacturing

Systems, 29, 130-141.

Malhotra, V., Raj, T. & Arora, A. 2009. Reconfigurable

manufacturing system: an overview. International

Journal of Machine Intelligence, 1, 38-46.

Mehrabi, M. G., Ulsoy, A. G. & Koren, Y. 2000.

Reconfigurable Manufacturing System and Their

Enabling Technologies. International Journal of

Manufacturing Technology and Management, 1, 113 -

130.

Moon, Y.-M. & Kota, S. 2002. Design of Reconfigurable

Machine Tools. Journal of Manufacturing Science and

Engineering, 124, 480 - 483.

Padayachee, J., Bright, G. & Masekamela, I. 2009.

Modular Reconfigurable Machine Tools: Design,

Control and Evaluation. South African Journal of

Industrial Engineering, 20, 127-143.

Saaty, T. L. 2008. Decision Making with the Analytic

Hierarchy Process. International Jourrnal of Services

Sciences, 1, 83-98.

Tang, L., Yip-Hoi, D. M., Wang, W. & Koren, Y. 2003.

Concurrent Line-Balancing, Equipment Selection and

Throughput Analysis for Multi-Part Optimal Line

Design. CIRP 2nd International Conference on

Reconfigurable Manufacturing. Ann Arbor, MI, USA.

ICINCO 2012 - 9th International Conference on Informatics in Control, Automation and Robotics

158