Design and Analysis of an Automated Heavy Vehicle Platoon

G´abor R¨od¨onyi

, P´eter G´asp´ar

, J´ozsef Bokor

and L´aszl´o Palkovics

Systems and Control Laboratory, Computer and Automation Research Institute, Hungarian Academy of Sciences,

Budapest, Hungary

Knorr-Bremse Brake-systems Gmbh, Budapest, Hungary

Keywords:

Vehicle Platoon, Peak-to-peak Gain, Model Set Identiﬁcation, Unfalsiﬁcation.

Abstract:

From the model set identiﬁcation through the control design and robust performance analysis to the implemen-

tation and experimental veriﬁcation, the whole design process for an automated vehicle platoon is presented.

The goal is to demonstrate that safe platooning with acceptable performance can be achieved by utilizing the

services already available on every commercial heavy trucks with automated gearbox. Using the services, the

control design reduces to the selection of four design parameters, the static gain coefﬁcients of the output-

feedback-input-feed-forward controller common for every vehicle. It is experimentally demonstrated, that in

normal driving maneuvers, the spacing errors are less than three meters.

1 INTRODUCTION

Safe control of vehicle platoons requiresstrict guaran-

teed bounds on inter-vehicle spacing errors. In order

to avoid collision the sampled errors are best mea-

sured by its ℓ

∞

norm, so the bounds represent the

worst-case peaks of the spacing errors. Consistent

identiﬁcation tools are the set membership methods in

the ℓ

setting, see e.g. (Gustafsson and M¨akil¨a, 1996;

Milanese and Belforte, 1982; Milanese, 1995). The

identiﬁed model sets are employed for on-line model

validation and a priori analysis of the control perfor-

mance measured by the worst-case spacing errors.

Controllers for autonomous vehicle platoons usu-

ally consists of two levels of feedback controllers. At

the lower level a local, vehicle speciﬁc controller is re-

sponsible for performing acceleration demands. The

higher level control law is common for all vehicle, it

is designed for satisfying string stability requirements

of the whole platoon. Very short safety gaps can be

guaranteed, under certain constraints on lead vehicle

maneuvers, when detailed engine, gearbox and brake

system models are available, see, e.g., in references

(Nouveliere and Mammar,2007; Gerdes and Hedrick,

1997; Liang et al., 2003). There is, however, some

difﬁculties in the widespread applicability of these

control methods. The required engine/gearbox/brake

system models are usually not available and not re-

liable for every commercial heavy trucks. Beyond

that, these controllers try to directly excite the brake

cylinder pressures and throttle valve of the engine,

which could also conﬂict with the existing control

units, such as Electronic Brake System (EBS) and En-

gine Control Unit (ECU).

In this paper the goal is to explore the performance

of an automated vehicle string where, in contrast to

the former solutions, only the standardized and gen-

eral services of the EBS and ECU are used. This

work is an extension of the work that have been pre-

sented in reference (R¨od¨onyi et al., 2012), where the

focus was placed on the analysis of the spacing error

bounds subject to heterogeneity in vehicle dynamics

and inter-vehicle communication failures. Here we

present two model set identiﬁcation problems, one of

which is an extension of the method introduced in

(Nagamune et al., 1997; Nagamune and Yamamoto,

1998).

In Section 2 the mathematical model of the pla-

toon is presented. The vehicle model set identiﬁca-

tion method is presented in Sections 3 and 4. The

performance of a heterogeneous platoon is analyzed

in Section 5. The experimental results are presented

in Section 6.

Basic notations. The peak norm of a sequence

u(k) is denoted by kuk

∞

=sup

|u(k)|, ℓ

∞

denotes

the space of sequences of ﬁnite peak norm. The

peak-to-peak norm of a system H is deﬁned by

kHk

=sup

u6=0

kHuk

∞

kuk

∞

Rödönyi G., Gaspár P., Bokor J. and Palkovics L..

Design and Analysis of an Automated Heavy Vehicle Platoon.

DOI: 10.5220/0004009900310037

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 31-37

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 STATE-SPACE MODEL OF

VEHICLE PLATOONS

In this section the discrete-time version of platoon

model and controller are brieﬂy summarized.

The longitudinal dynamics of a single vehicle is

approximated by the following ﬁrst order nominal

model with sampling time T

(k+ 1) = θ

∗

(k) + θ

∗

(k), i = 0,1,...,n

where a

and u

denote the acceleration and accelera-

tion demand of vehicle i, θ

∗

and θ

∗

denote constant

parameters.

The spacing error of the ith follower vehicle is de-

ﬁned by e

(k) = x

(k) + L

− x

i−1

(k) where L

denotes

the desired intervehicular space. Without loss in gen-

erality it can be assumed to be zero in the analysis.

The position of the ith vehicle is denoted by x

. For

each vehicle, the spacing error dynamics can be writ-

ten as follows





(k+ 1)









1 T

0 0 0

0 1 T

−T

0 0 θ

∗

0 θ

∗











(k)

i−1

(k)







where δ

denote the relative speed of vehicle i and

i− 1. The open-loop model of the whole platoon

x(k+ 1) = A

x(k) + B

u(k) + E

r(k)

is constructed by introducing the state vector x

··· e

], control input vector u

··· u

] and reference signal r = u

The platoon controller is a modiﬁed version of

the constant spacing strategy presented in (Swaroop,

1994, Section 3.3.4). The modiﬁcation resides in

that, instead of measured acceleration, control input

is transmitted through the network. Consequently, the

gear change has lower impact in the control signal

than in the acceleration, so each vehicle can change

gear without deceiving the followers; the vehicles re-

act quicker to maneuver changes; and no need for

ﬁltering the rather noisy acceleration measurements.

The control strategy is deﬁned by the following equa-

tions

u(k) := u

(k) + ˆu

(k)

(k) = K

x(k)

(k) = K

x(k) + G

r(k) + Su(k)

where u

contains the locally available radar informa-

tion. Gain matrix K

can be constructed based on the

following deﬁnition

L,1

(k) = −k

(k) − k

(k)

L,i

(k) = −k

1β

(k) − k

2β

(k), i > 1

where i stands for the vehicle index and k

+λ+λq

1+q

, k

λ(q

)

1+q

, k

1α

+λq

1+q

, k

2α

λq

1+q

, k

1β

+λ

1+q

and k

2β

λq

1+q

, where q

, q

and λ are design parameters. Control signal u

is con-

structed from the information received from the com-

munication network

N,1

(k) = u

(k)

N,i

(k) =

1+ q

i−1

(k) +

1+ q

(k)

−k

1α

∑

j=0

(k) − k

2α

∑

j=0

(k), i > 1

from which K

, G

and S matrices can be con-

structed.

The communication network has a sampling time

of T = NT

and the packet is transmitted after h <

T constant delay. If y(k) denotes the variable to be

transmitted at the network input, then

ˆy(k) =



y(k− h) if

k−h

is an integer

ˆy(k− 1) otherwise

denotes the network output at the receiver.

The closed-loop system with the delayed commu-

nication is derived in (R¨od¨onyi et al., 2012). The lo-

cal part u

of the controllers run with the faster sam-

pling rate T

. By closing the loop with u

, re-sampling

with NT

, then closing the loop with ˆu

and assuming

r(k) = r(k + 1) = ... = r(k + N − 1) we arrive at the

following system

z(k+ N) = A

(h)z(k) + E

(h)r(k)

(h) =



+ B

+ SK

) B

+ B

+ SK



(h) =



+ B



where the state-space is augmented to

z(k) =



x(k)

(k− N)



and

h−1

∑

j=0

N−1− j

, B

N−1

∑

j=h

N−1− j

N−1

∑

j=0

N−1− j

where A

= A

+ B

, B

= B

, E

= E

. The spac-

ing errors can be observed through matrixes C

(k) = C

z(k), i = 1, 2,...n.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

3 IDENTIFICATION OF MODEL

SETS

Nominal vehicle models and uncertaintysets are iden-

tiﬁed in the worst-case ℓ

setting. Two circum-

stances motivate the application of this identiﬁcation

approach. Both the brake system and the drive-line

are functioning as an unknown nonlinear, hybrid sys-

tems with many thousands of program rows organiz-

ing ﬁnite state machines. A good description of noise

statistics is not available and only reduced order mod-

els can be considered. It seems to be reasonable to

consider only strict bounds on the disturbances and

unmodelled dynamics. Strict bounds are also useful

in the worst case analysis of spacing error bounds. On

the other hand, these model sets may result in overly

conservative (loose) description of the system. So-

phisticated uncertainty model structures are required

for control performance analysis problems, the elabo-

ration of which is yet left to future work.

In order to obtain a preliminary view of the uncer-

tainty in the vehicle dynamics and actuators including

EBS and ECU softwares, two identiﬁcation methods

are presented in the section. The ﬁrst one is an ARX-

type model structure with time-varying parameters.

The basic concept originates in the papers (Nagamune

et al., 1997; Nagamune and Yamamoto, 1998), brieﬂy

presented in the following subsection. Then, these re-

sults are extended in several ways in Section 3.2. In

the second method an OE model structure is identiﬁed

in Section 3.4. Both methods are applied for experi-

mental data of a heavy truck in Section 4.

3.1 Identiﬁcation of Smallest Unfalsiﬁed

Sets

Consider the following discrete-time linear single in-

put single output model structure

G(z) =

∑

i=1

−i

∑

i=1

−i

, θ ∈ P

(θ

∗

,ε)

with time-varying parameter vector θ =

,...,a

,...,b

]

deﬁned in the cube

(θ

∗

,ε

) := {θ : kW(θ

∗

− θ)k

∞

≤ ε}, where the a

priori given diagonal matrix W = diag{

θ,1

,...,

θ,2m

}

deﬁnes the shape of the cube with edges of length

2ε

θ,i

. Given input output data set {u(k),y(k)}

k=1

the problem is to ﬁnd the central parameter θ

∗

and

the minimal size ε of the cube such that for every

k = m,...,l there exists a parameter θ ∈ P

(θ

∗

,ε) not

invalidated by the measurements, i.e.

(θ

∗

,ε) ∩ D

0 ∀k = m,..., l

where D

:= {θ : y(k) = ϕ

(k)θ(k)} and ϕ

(k) =

[−y(k−1),...,−y(k− m),u(k−1),...,u(k− m)]. This

problem can be solved by minimizing a convex func-

tion as follows

ε = min

∗

max

m≤k≤l

|y(k) − ϕ

(k)θ

∗

−1

ϕ(k)k

In the following subsection the model structure is

augmented by an additive disturbance term, and the

worst case prediction error is minimized while an op-

timal shape of the parameter cube and a bound for the

disturbance are determined.

3.2 Unfalsiﬁed ARX Model Set of

Minimal Prediction Error in ℓ

∞

With the notation of the previous section we can de-

ﬁne the following ARX type model structure, denoted

by M

M = { y(k) = ϕ

(k)θ(k) + e(k),

θ(k) ∈ P

(θ

∗

,ε

e(k) ∈ P

(ε

), k = 1,..., l }

where

(θ

∗

,ε

) = {θ : kW(θ

∗

− θ)k

∞

≤ 1},

(ε

) = {e : |e| ≤ ε

= [ε

θ1

,...,ε

θ2m

]

W = diag



θ,1

,...,

θ,2m



The shape and size of the uncertainty set char-

acterized by ε

and ε

are unknown parameters.

The only information given a priori is the data set

{u(k), y(k)}

k=1

In order to characterize consistency of the model

set with the data, deﬁne hyperplane D

in the n+1 di-

mensional extended parameter space of p := [θ

:= {p : y(k) = [ϕ

(k) e(k)]p}

Let P(θ

∗

,ε

) := {p = [θ

: θ ∈ P

(θ

∗

,ε

), e ∈

(ε

)} denote the parameter set deﬁning model set

M in the extended parameter space.

Deﬁnition 1 (Consistency). The parameter set p ∈

P(θ

∗

,ε

) can reproduce the data if

P(θ

∗

,ε

) ∩ D

0 ∀k = m,..., l (1)

For given data ϕ(k) and model set parameters θ

∗

and ε

the output y(k) that the model set can gen-

erate lies between the bounds

¯y(k) = max

θ∈P

(θ

∗

,ε

)

(k)θ+ ε

y(k) = min

θ∈P

(θ

∗

,ε

)

(k)θ− ε

DesignandAnalysisofanAutomatedHeavyVehiclePlatoon

With these bounds, the parameter set identiﬁcation

problem can be formulated as follows.

Problem 1. Assume that we are given a data set

{u(k), y(k)}

k=1

. Find a model set characterized by

∗

, ε

and ε

such that (1) is satisﬁed and that mini-

mizes γ :=

k ¯y(k) − y(k)k

∞

3.3 Solution Via Linear Programming

It will be shown that Problem 1 leads to the solution of

a linear programming (LP) problem. In contrast to the

solution of (Nagamune et al., 1997), where for each

a minimum necessary size parameter ε = ε(D

,θ

∗

)

is determined for a given θ

∗

, we characterize consis-

tency with the help of the output bounds

Lemma 3.1. Consistency condition (1) is satisﬁed if

and only if there exist θ

∗

, ε

and ε

such that

y(k) ≤ ϕ

(k)θ

∗

+ |ϕ

(k)|ε

+ ε

, k = m,..., l (2)

y(k) ≥ ϕ

(k)θ

∗

− |ϕ

(k)|ε

− ε

, k = m,..., l (3)

where |.| element-wise takes the absolute value of the

argument.

Proof. We only need to show that

max

θ∈P

(θ

∗

,ε

)

(k)θ = ϕ

(k)θ

∗

+ |ϕ

(k)|ε

and

min

θ∈P

(θ

∗

,ε

)

(k)θ = ϕ

(k)θ

∗

− |ϕ

(k)|ε

, then

the statement follows from the deﬁnitions. The linear

function ϕ

(k)θ over a convex polytope takes up its

extreme values at the vertices of the polytope. Let the

vertex set of P

(θ

∗

,ε

) be denoted by V ,

V =











θ : θ = θ

∗







±ε

θ,1

±ε

θ,2m

















where ± means all combinations. From this the

claims follow.

The following theorem summarizes our results.

Theorem 3.2. The model set M which is consistent

with the data set {u(k), y(k)}

k=1

and minimizes γ =

k ¯y(k) − y(k)k

∞

is the solution of the following LP

problem.

min

∗

,ε

subject to (2), (3) and

γ ≥ |ϕ

(k)|ε

+ ε

, k = m,...,l

The problem involves 4m + 2 variables and 3(l −

m + 1) inequality constraints, and can be efﬁciently

solved by rutin CLP in the MPT toolbox for Matlab,

(Kvasnica et al., 2004).

3.4 Identiﬁcation of OE Models of

Minimal Error in ℓ

∞

In this section an output error model structure is iden-

tiﬁed with the smallest error in ℓ

∞

. Suppose, we are

given a data set {u(k),y(k)}

k=1

and the model struc-

ture of LTI SISO systems in the form

G(z) =

∑

i=1

−i

∑

i=1

−i

The set of parameters is divided as θ

= [a

,...,a

]

and θ

= [b

,...,b

]. We are looking for θ

and θ

that

minimize γ := ky(k)− ˆy(k)k

∞

, where ˆy(z) = G(z)u(z).

This optimization problem is nonlinear in parameter

, therefore an nonlinear programming method can

be applied. In case of small noises, good initialization

for θ

and determination of the model order can be

attained by using the recent result (Soumelidis et al.,

2011). Once θ

is ﬁxed, θ

can be computed by linear

programming as follows.

1. Formulate A, B,C, the controllability canonical

state-space representation of G(z). Then C = θ

From this, ˆy(k) = θ

∑

k−1

j=0

k− j−1

Bu( j)

2. Solve the LP problem

min

subject to

y(k) − θ

k−1

∑

j=0

k− j−1

Bu( j) ≤ γ, k = m, ...,l

−y(k) + θ

k−1

∑

j=0

k− j−1

Bu( j) ≤ γ, k = m, ...,l

4 MODELLING LONGITUDINAL

VEHICLE DYNAMICS

Several braking experiments have been carried out

with a Volvo FH, 24 tonne three-axle truck. ARX and

OE models of order m = 1 are identiﬁed by using the

methods described in the previous section.

4.1 ARX Model Structure

The LP method of Theorem 3.2 was applied to the

model structure

a(k) = a(k− 1)θ

(k) + u(k− 1)θ

(k) + e(k)

θ(k) := [θ

(k) θ

(k)]

∈ P

(θ

∗

,ε

)

ke(k) − e

∗

∞

≤ ε

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

where a(k) is the longitudinal acceleration computed

by the available onboard computers based on wheel

speed measurements, and u(k) is the acceleration de-

mand deﬁned in an AutoBox connected to the vehi-

cle’s CAN network. An offset error of the measure-

ments can be taken into consideration with parame-

ter e

∗

. The unknown parameters of the model are the

central parameters θ

∗

and e

∗

, and the bounds of the

parameter and noise variation, ε

and ε

, respectively.

The one-step ahead prediction of the optimal

model is plotted in Figure 1. The central parameters

∗

and θ

∗

correspond to a time constant of 1.13s and

a gain of 9.5 when the model is transformed to con-

tinuous time by zero order hold (T

= 0.01). For the

parameter variation we get ε

= [0.180.20]1e− 12.

0 2 4 6 8 10 12

−5

−4

−3

−2

−1

time [s]

acceleration [m/s

]

1−step ahead prediction

command

measured

central model

bounds

Figure 1: One step ahead prediction with the central model

with parameter θ

∗

in a braking experiment. Bounds for the

prediction, ¯y and y, are also plotted (thin dotted black lines).

Fixing the maximum allowed noise level ε

, the

optimization can be performed in the remaining vari-

ables. Figures 2 and respectively 3 show the depen-

dence of the prediction error bound and the optimal

parameters on the chosen noise levels. It can be seen

that forcing the model set to represent uncertainty by

the time-variation of parameters will result in overly

conservative models. At the optimum, the uncertainty

is described by almost entirely the noise term. We

must conclude that a more sophisticated uncertainty

description is necessary.

0 0.1 0.2 0.3 0.4 0.5

Prediction error bound as a function of fixed noise bound

fixed noise bound, ε

(minimal γ at ε

=0.14282)

Prediction error bound, γ

Figure 2: Worst case prediction error as a function of ﬁxed

noise bound ε

in the ARX model structure.

0 0.1 0.2 0.3 0.4 0.5

−0.5

0.5

1.5

2.5

fixed noise bound, ε

(minimal γ at ε

=0.14282)

Parameters θ

and θ

Optimal parameter bounds as functions of fixed noise bound

bounds

Figure 3: Parameter bounds as functions of ﬁxed noise

bound ε

in the ARX model structure.

4.2 OE Model Structure

The output-error model structure

a(k) = a(k− 1)θ

+ u(k − 1)θ

+ e(k) − e(k − 1)θ

ke(k) − e

∗

∞

≤ ε

is identiﬁed by applying the LP method presented in

Section 3.4 for identifying θ

while θ

is determined

by simple line search. The optimal parameters cor-

respond to a time constant of 0.9s and a gain of 1.25

when the model is transformed to continuous time by

zero order hold (T

= 0.01). The ﬁt of the model and

the error bounds are plotted in Figure 4. This model

can serve as nominal models in the performance anal-

ysis of the platoon.

0 2 4 6 8 10 12

−5

−4

−3

−2

−1

time [s]

acceleration [m/s

]

Output−error model fit

command

measured

central model

bounds

Figure 4: Fit of the OE model with parameter to the mea-

surements in a braking experiment. Bounds for the error are

also plotted (thin dotted black lines).

5 PERFORMANCE ANALYSIS OF

HETEROGENEOUS PLATOONS

For the case of heterogeneous platoons with nom-

inal LTI models, spacing error bounds in ℓ

∞

are

analyzed.Assume that the allowable reference input

r = u

satisﬁes ku

∞

≤ u

max

, where u

max

is a given

bound. Then, the worst-case peaks of the spacing er-

rors, as functions of communication delays, can be

DesignandAnalysisofanAutomatedHeavyVehiclePlatoon

computed as follows

(h) := k e

(h,t)k

∞

∑

j=0

(h)t

(h)|u

max

In the following numerical analysis ε

(h), i = 1,...,n,

are computed when the platoon is not homogeneous

in nominal vehicle parameters θ

∗

. It is assumed that

both θ

∗

i,1

and θ

∗

i,2

may differ from vehicle to vehicle

Θ = [θ

∗

1,1

∗

1,2

∗

2,1

∗

2,2

... θ

∗

n,1

∗

n,2

∗

i,1

= 1−

∗

i,2

∈ {0.6, 0.8}

∈ {0.9,1.1}

where time constant τ

and gain g

are parameters of

the continuous-time vehicle models and may take up

their extremal values. It can be shown that the worst-

case platoon conﬁguration is the case when the vehi-

cle model parameters are extremal and alternating in

order. This means that if the platoon is of length n+1,

it is enough to compute ε

(h), i = 1,...,n for (n+ 1)

systems. Taking the maximum and minimum for the

(n + 1)

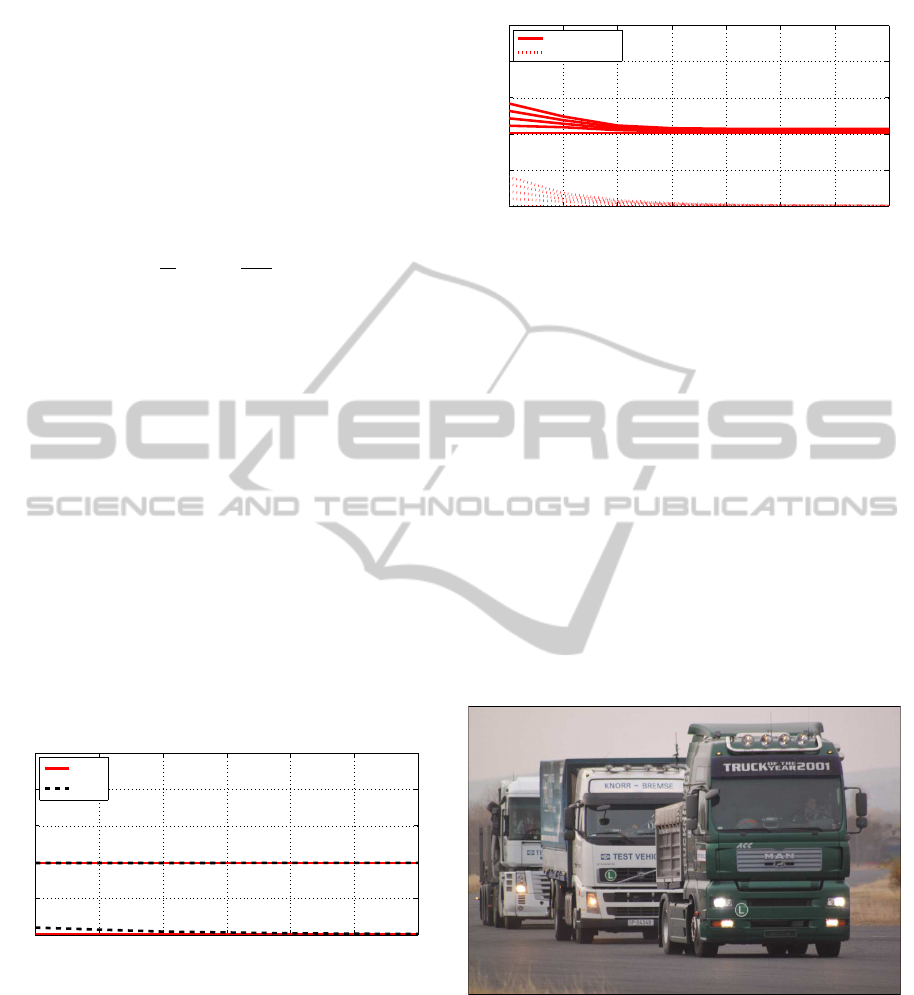
systems, Figure 5 show the worst case and

best case bounds as functions of the vehicle index i.

The lower bounds are achieved in case of homoge-

neous platoons. For a given set of allowable maneu-

vers, this analysis directly provides hints on choosing

safety gaps between the vehicles in the different con-

trol modes, such as L

> ε

, assuming zero initial con-

ditions. The analysis is carried out for a range of net-

work delays from h = 0 to h = 8T

, but network delay

of this range has negligible impact on the bounds.

1 1.5 2 2.5 3 3.5 4

Vehicle index

Spacing error bound [m]

Peak bounds for spacing errors with different delays

h=0T

h=8T

Figure 5: Lower and upper bounds on spacing errors, ε

for

different network delays. Uncertainty is present in both θ

and θ

. Lower bounds (around zero) correspond to homo-

geneous platoons. Upper bounds at ε

= 4 correspond to

platoons of alternating vehicle dynamics.

In the case when gain coefﬁcients are estimated

on-line, for example with the help of parameter adap-

tation methods described in (Swaroop, 1994), acceler-

ation demand can always be scaled so that θ

param-

eters can be set to θ

= 1. Then, spacing errors are

bounded as shown in Figure 6. The bounds reduced

to about one meter.

1 2 3 4 5 6 7 8

0.5

1.5

2.5

h=0T

Vehicle index

Spacing error bound [m]

Peak bounds for spacing errors with different delays

h=8T

upper bounds

lower bounds

Figure 6: Lower and upper bounds on spacing errors, ε

for

different network delays. Uncertainty is present only in θ

6 EXPERIMENTAL RESULTS

The control strategy presented in Section 2 is imple-

mented on a platoon of three heavy trucks and tested

on a 3km long ﬂight-strip. The leader vehicle, driven

by a driver, is a MAN TGA two-axle tractor of 18

tonne with load cage. The second vehicle is a Volvo

FH 24 tonne three-axle truck. The third one is a Re-

nault Magnum two-axle tractor of 18 tonne with a

semitrailer, See Fig. 7. It is important to remark that

all vehicles are equipped with automatic gear change,

thus acceleration can be attained purely by software.

The communication network consists of radio

transceivers operating on the open 868MHz ISM

narrow-band.

Figure 7: Experimental vehicles in project TruckDAS.

The experimental scenario is started with a ’join-

ing in’ maneuver in which the leader vehicle passes

the others which are travelling at constant speed.

When the last vehicle in the platoon is caught by the

radar of the joining vehicle and its driver enables the

joining maneuver by pressing a deadman-button, the

joining vehicle is accelerated and braked by given

constant values and for sufﬁcient time so that the ve-

hicle arrives approximately at the prescribed distance

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

with speed near that of the platoon. After the braking

period the spacing controller is switched on. When

both joining maneuvers are ﬁnished, the leader vehi-

cle can accelerate and decelerate and ﬁnally stop.

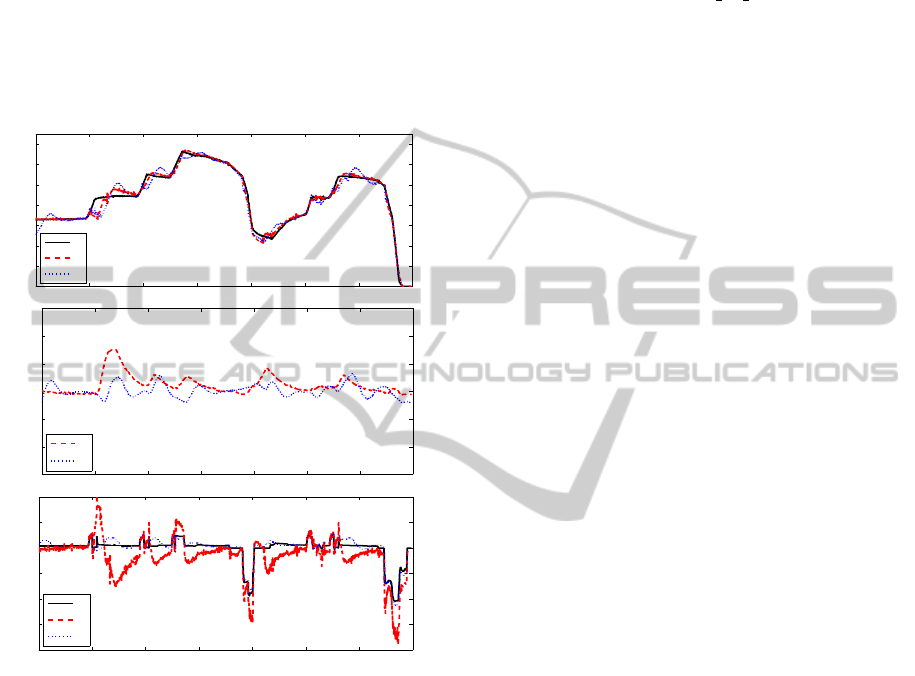
Nine experiments of similar maneuvers were car-

ried out on a 3km long pathway. The maximum spac-

ing error was not greater than 3m during braking, i.e.

in the direction of collision danger. During driving

maneuvers, the maximum leg was not greater than

8m.

0 20 40 60 80 100 120 140

Communication with both preceding and leader vehicle

speed [km/h]

0 20 40 60 80 100 120 140

−15

−10

−5

spacing error [m]

0 20 40 60 80 100 120 140

−4

−3

−2

−1

Control signal [m/s

]

time [s]

Figure 8: Platoon control experiment.

7 CONCLUSIONS

According to our experiences in a platoon of three ve-

hicles with different types and properties, a safety gap

of 3m can be safe if the following conditions hold:

deceleration of the leader vehicle is not greater than

2m/s

and there is some dwell time between inten-

sive acceleration and abrupt braking maneuvers so

that transients can cease.

ACKNOWLEDGEMENTS

This research work has been supported by Control

Engineering Research Group, Hungarian Academy of

Sciences at the Budapest University of Technology

and Economics and the Hungarian National Scien-

tiﬁc Research Fund (OTKA) through grant No. CNK-

78168. The research has also been supported by the

Hungarian National Ofﬁce for Research and Technol-

ogy through the project TECH 08 A2 /2-2008-0088.

REFERENCES

Gerdes, J. and Hedrick, J. (1997). Vehicle speed and spac-

ing control via coordinated throttle and brake actua-

tion. Control Engineering Practice, 5:1607–1614.

Gustafsson, T. K. and M¨akil¨a, P. M. (1996). Modelling of

uncertain systems via linear programming. In Auto-

matica, volume 32. No. 3, pages 319–335.

Kvasnica, M., Grieder, P., and Baoti´c, M. (2004). Multi-

Parametric Toolbox (MPT).

Liang, H., Chong, K. T., No, T. S., and Yi, S. (2003). Vehi-

cle longitudinal brake control using variable param-

eter sliding control. Control Engineering Practice,

11:403–411.

Milanese, M. (1995). Properties of least squares estimates

in set membership identiﬁcation. In Automatica, vol-

ume 31. No. 2, pages 327–332.

Milanese, M. and Belforte, G. (1982). Estimation theory

and uncertainly intervals evaluation in presence of un-

known but bounded errors: Linear families of models

and estimators. In IEEE Trans. on Automatic Control,

volume AC-27. No. 2, pages 408–414.

Nagamune, R. and Yamamoto, S. (1998). Model set

validation and update for time-varying siso systems.

In Proceedings of the American Control Conference,

Philadelphia, pages 2361–2365.

Nagamune, R., Yamamoto, S., and Kimura, H. (1997).

Identiﬁcation of the smallest unfalsiﬁed model set

with both parametric and unstructured uncertainty.

In Preprints of the 11th IFAC Symposium on Sys-

tem Identiﬁcation (SYSID97), Kitakyushu, Japan, vol-

ume 1, pages 75–80.

Nouveliere, L. and Mammar, S. (2007). Experimental ve-

hicle longitudinal control using a second order slid-

ing mode technique. Control Engineering Practice,

15:943–954.

R¨od¨onyi, G., G´asp´ar, P., Bokor, J., Aradi, S., Hankovszki,

Z., Kov´acs, R., and Palkovics, L. (2012). Analysis and

experimental veriﬁcation of faulty network modes in

an autonomous vehicle string. In 20th Mediterranean

Conference on Control and Automation, Barcelona,

Spain.

Soumelidis, A., Schipp, F., and Bokor, J. (2011). Pole

structure estimation from laguerre representations us-

ing hyperbolic metrics on the unit disc. 50th IEEE

Conference on Decision and Control and European

Control Conference (CDC-ECC), Orlando, FL, USA.

Swaroop, D. (1994). String stability of interconnected sys-

tems: An application to platooning in automated high-

way systems. PhD dissertation.

DesignandAnalysisofanAutomatedHeavyVehiclePlatoon