Elastomeric Seismic Isolators Behavior at Different Pads Thickness
Gabriele Milani
1
and Federico Milani
2
1
Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133, Milan, Italy
2
Chem. Co Consultant, Via J. F. Kennedy 2, 45030, Occhiobello (RO), Italy
Keywords: Elastomeric Isolators, Hardness/Young’s Modulus, Elastic Modulus/Thickness, Stretch-stress and Shear
Behavior under Large Deformations, Numerical Simulations, Finite Element Method.
Abstract: A seismic isolator has the main function to be extremely deformable for horizontal forces, but at same time
sufficiently stiff when loaded with vertical actions. These properties may be strongly influenced by both the
isolator geometry (i.e. overall dimensions, number and thickness of rubber pads and steel laminas) and the
mechanical properties of rubber pads. Mechanical properties of the pads, especially Young modulus, may be
evaluated as a function of hardness, by means of consolidated empirical formulas. In this work, the
influence of rubber pads thickness and hardness on both vertical and horizontal stiffness of realistic seismic
isolators is discussed. Three full 3D Finite Element models referred to three different seismic isolators
having different slenderness are analysed in detail in both vertical compression (elastic analysis) and simple
shear in large deformations. Uniaxial and shear response of the seismic devices obtained numerically are
finally critically compared, with the aim of evaluating the best compound to be used in practice.
1 INTRODUCTION
In the recent past, seismic isolation technology has
been applied almost entirely to large buildings in
high seismicity countries, where seismic events are
expected to be relevant. One of the most diffused
technology for seismic isolation is the utilization of
elastomeric multilayer bearings. Until now, the high
cost of production reduces the use of seismic
isolation mainly for important buildings. Their cost
is due to the preparation of the steel plates, which
are used to provide vertical stiffness, and the
assembly of the rubber sheets. From a technical
point of view, the rubber has the main function to be
extremely deformable for horizontal forces, but at
the same time sufficiently stiff when loaded with
vertical actions. Each individual elastomeric layer in
the bearing deforms according to two kinematic
assumptions, i.e. that (1) horizontal planes remain
planar and (2) points on vertical lines lie on a
parabola after loading.
This is obtained thanks to the incompressibility
of the rubber sheets (Amin et al., 2002; 2006, Gracia
et al., 2010) and the introduction of the thin
reinforcing steel plates, interspersed between 10-30
mm thick rubber pads (Moon et al., 2002; 2003).
Kelly and co-workers (e.g. Tsai and Kelly, 2002)
have demonstrated that theoretically it is possible to
substitute reinforcing elements of multilayer
elastomeric isolation bearings, which are normally
steel plates, by fiber reinforcement. This solution
goes to a drastically reduction in the weight and
probably in the reduction of the cost in the assembly
of the items. Milani & Milani (2012) have described
a numerical approach to predict the macroscopic
behavior of parallelepiped elastomeric isolators
undergoing large deformations. In that work, the
actual behaviour of elastomeric sheets as a function
of the typology of rubber used and their compounds
were discussed. Following the original approach
proposed in Milani & Milani (2012), in the present
work, with the aim of reducing the production cost,
we have theoretically considered the opportunity to
increase the thickness of the rubber sheets and
decrease the steel plates. This geometrical
rearrangement provides a decrease of the vertical
stiffness but at the same time a good performance
under horizontal loads. When the rubber pad
thickness is increased up to 3.5 cm, it would be
necessary to consider the kinetic of vulcanization of
the rubbers sheets, in order to obtain mechanical-
elastomeric characteristics as homogeneous as
possible in any point of the rubber pad. This would
allow to obtain responses for horizontal forces of the
17
Milani G. and Milani F..
Elastomeric Seismic Isolators Behavior at Different Pads Thickness.
DOI: 10.5220/0004012000170023
In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),
pages 17-23
ISBN: 978-989-8565-20-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

isolator similar to those obtained with thin sheets. As
it is known, the mechanical elastic behavior can be
correlated to the density of the cross-link, that is
function of the thickness, the dimensions, the type of
rubber and the compound. For these reasons, it is
necessary to optimize the vulcanization in terms of
time/temperature in such a way that in all points of
the items there are similar mechanical-elastomeric
characteristics and in order to obtain pads with a
hardness directly proportional to pad thickness. As a
matter of fact, mechanical properties of the pads,
especially Young modulus, at a first attempt and
without the possibility to perform expensive
mechanical simulations, may be evaluated as a
function of hardness, by means of consolidated
empirical formulas. In this work, the influence of
rubber pads thickness and hardness on both vertical
and horizontal stiffness of realistic seismic isolators
is discussed. Three full 3D Finite Element models
referred to three different seismic isolators having
different slenderness (and hence thickness of the
rubber pads) are analysed in detail in both vertical
compression (elastic analysis) and simple shear in
large deformations. Uniaxial and shear response of
the seismic devices obtained numerically are finally
critically compared, with the aim of evaluating the
best compound to be used in practice.
2 CURED RUBBER
MECHANICAL PROPERTIES
AS A FUNCTION OF
HARDNESS
At present, the influence of pads thickness in the
seismic isolation performance of rubber bearings is
not completely understood in terms of types of
elastomers, optimal recipe, ingredients of
vulcanization to be used to increase both the
mechanical performance and reduce costs. In this
paper, three different thicknesses of rubber pads are
considered and the vertical stiffness of the isolators
so obtained is evaluated in conjunction with the
shear behavior.
As a matter of fact, the utilization of thick pads
provides a decrease of the vertical stiffness, which
obviously depends on the elastic modulus of the
rubber used.
In general, the so-called static modulus of a
rubber compound is obtained in standard stress-
strain tests in which the samples are extended at the
rate of 20 in/min. The dynamic modulus is measured
while the sample is oscillated about some given
strain or stress, usually under some fixed
superimposed load. Hardness is a modulus measured
at very small deformations, commonly obtained by
means of the use of indenter devices.
The static moduli at 300% extension, the
dynamic moduli and the hardness data have been
extensively studied by Studebaker & Beatty (1978).
Usually modulus and hardness of a stock are
increased through the use of fillers. As a
consequence, both modulus and hardness depend on
the so called filler “structure” (or more specifically
on carbon black structure) and cross-linking density.
Dealing with commercial compounds, which are
rather random and heterogeneous, it is difficult to
collect data regarding Young modulus and hardness
and draw any generalization.
The standard test method to have an idea of
rubber mechanical properties still remains
ASTMD2240, which deals with the penetration of a
specified indentor forced into the material under
specified conditions. The test is called “durometer
test”.
Durometer, like many other hardness tests,
measures the depth of an indentation in the material
created by a given force on a standardized presser
foot. This depth is dependent on the hardness of the
material, its viscoelastic properties, the shape of the
presser foot, and the duration of the test. ASTM
D2240 durometers allows for a measurement of the
initial hardness, or the indentation hardness after a
given period of time. The basic test requires
applying the force in a consistent manner, without
shock, and measuring the hardness (depth of the
indentation). If a timed hardness is desired, force is
applied for the required time and then read. The
material under test should be a minimum of 6.4 mm
(.25 inch) thick.
There are some empirical formulas that correlate
indentation hardness to penetration, elastic modulus
and viscoelastic behavior of the material.
For instance, the following external force-
hardness empirical law holds for a so called type A
durometer:
A
HN 075.0550.0:Force +=
(1)
where H
A
is the hardness read on a type A
durometer.
Conversely, for a so called type B durometer the
following formula may be used:
D
HN 4445.0:Force =
(2)
where H
D
is the hardness reading on a type D.
The difference between type A and type D
durometers stands exclusively on the geometry of
SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
18

the device.
Type A durometer is a hardened steel rod with
diameter 1.1- 1.4 mm, with a truncated 35° cone of
diameter 0.79 mm. Type D durometer is a hardened
steel rod having a diameter of 1.1- 1.4 mm, with a
30° conical point and 0.1 mm radius tip.
Under small deformations rubbers are linearly
elastic solids. Because of the high modulus of bulk
compression, about 2000MN/m
2
, compared to the
shear modulus G, about 0,2-5MN/m
2
(Tobolsky and
Mark, 1971), they may be regarded as relatively
incompressible. The elastic behavior under small
strains can thus be described by a single elastic
constant G, being Poisson’s ratio very near to ½ and
Young’s modulus E equal to 3G with very good
approximation.
In order to have the possibility to evaluated the
relation between hardness and Young’s modulus,
first of all we have taken into consideration a semi
empirical relation between the shore hardness and
Young’s modulus for elastomers that has been
derived by Gent (1958; 1978). This relation has the
following form:
()
()
S54.2254137505.0
S62336.7560981.0
−
+
=E
(3)
where E is the Young’s modulus in MPa and S is the
shore hardness. This relation gives a value of E
equal to infinite at S=100, but departs from
experimental data for S lower than 40.
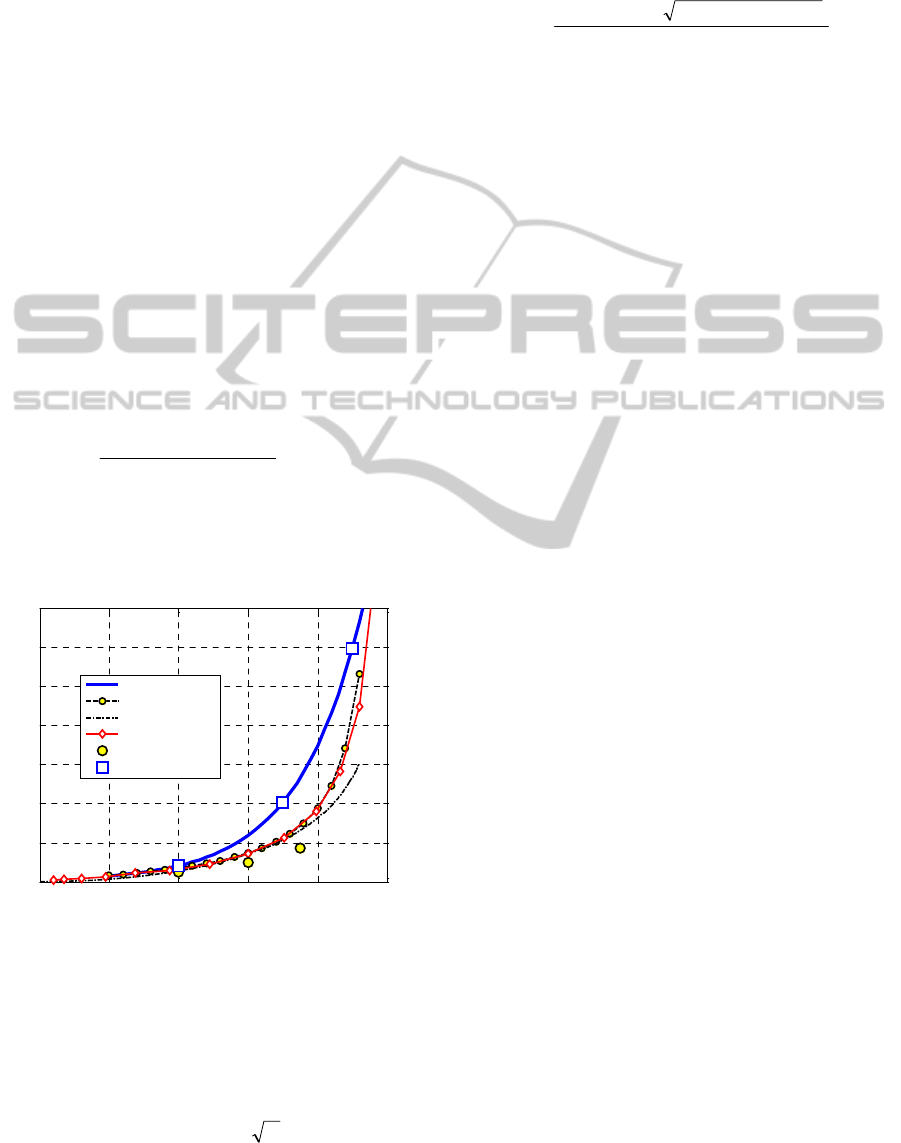
Figure 1: Empirical dependence of the rubber elastic
modulus in terms of international hardness (formula
(6).
Circle, square and triangle denote elastic moduli used in
the numerical simulations.
Another relation that fits experimental data
slightly better is the following and is reported into
British standards (BS 1950, BS 1957):
(
)
Eerf
4
10186.3100S
−
×=
(4)
where erf is the error function and E is in units of
Pa. A first order estimate of the relation between
shore D hardness and the elastic modulus for a
conical indenter with a 15 degree cone is:
(
)
E
E
D
88.78136.6113188.7820
100S
++−
−=
(5)
where S
D
is the shore D hardness and E is in MPa.
Another linear relation between the shore
hardness and the natural logarithm of Young’s
modulus is applicable over a large range of shore A
and shore D hardness (Qi et al., 2003). This relation
has the form:
6403.0S0235.0)ln( −=E
(6)
Where S= S
A
for S
A
between 20 and 80 and S=
S
D
+50 for S
D
between 30 and 85, being S
A
the shore
A hardness, S
D
the shore D hardness and E the
Young’s modulus in MPa.
In our theoretical work, we have considered an
ideal rubber item with different hardness and have
calculated the corresponding Young’s modulus.
From that value, we have deduced the influence of
the thickness of the compounding rubber materials
for the optimal stiffness vertical resistance.
However, hardness is a superficial determination and
for this reason it is necessary to optimize also the
density of cross-linking at same recipe. While this
latter issue is extremely important, our work focuses
on the possibility to increase the thickness of rubber
pads to optimize the elastic properties of the items,
such as initial compression modulus and shear
behavior under large deformation.
The typical dependence of rubber Young
modulus E with respect to hardness S, obtained by
means of the empirical formulas discussed above is
schematically represented in
Figure 1.
As it is possible to notice and as expected, there
is a quite large scatter of the results for rubbers with
big hardness. However, formulas suggested by
ASTM 1415 and BS 903 provide very similar results
in a wide range, also for S near 80. Despite the fact
that Qi et al., (2003) formula seems less
conservative for hard rubbers, authors adopted such
approach to evaluate Young modulus to use in the
numerical simulations, being Qi et al., (2003)
approach based on a convincing experimental and
theoretical framework.
0 20 40 60 80 100
0
5
10
15
20
25
30
35
Hardness S
Young Modulus [MPa]
Qi et al. (2003)
Gent (1958)
BS 903 (1957)
ASTM 1415
FIP experimental
Present data
ElastomericSeismicIsolatorsBehavioratDifferentPadsThickness
19

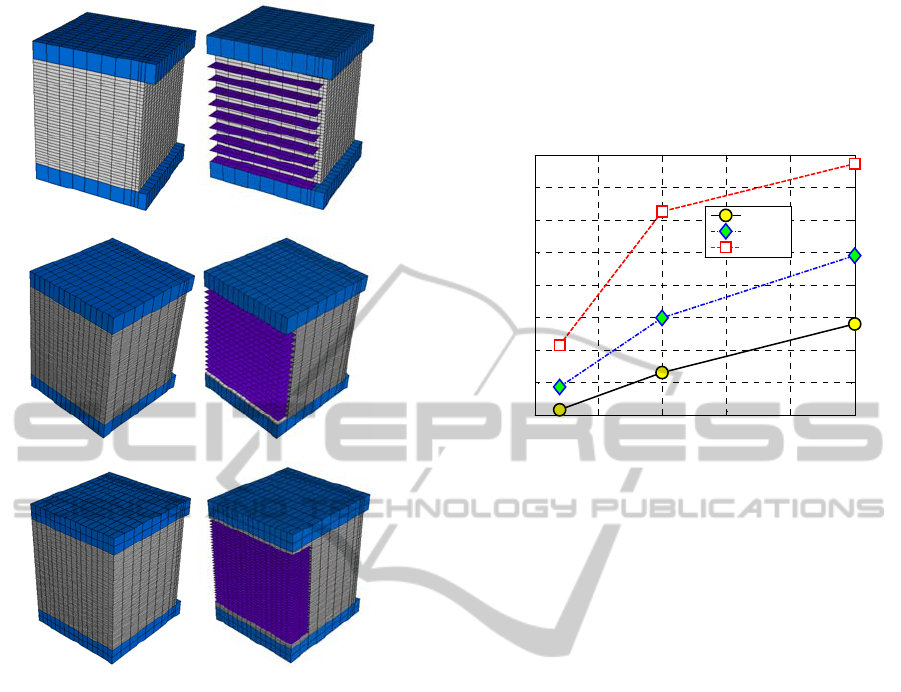
Figure 2: FE discretization of the seismic isolators studied.
3 NUMERICAL FINITE
ELEMENT SIMULATIONS ON
ELASTOMERIC ISOLATORS
One of the key parameters having a fundamental
role in the determination of overall isolator
compression elastic modulus E
c
is the so called
shape factor S
F
(or primary shape factor), defined as
the ratio between the loaded area and the lateral
surface free to bulge. Since the shape factor refers to
the single rubber layer, it represents a measure of the
local slenderness of the elastomeric bearing.
Experimental tests have shown that low shape factor
bearings, characterized by values of S
F
greater than
5 and less than 20 (in the present case S
F
=7), provide
an isolation effect in both the horizontal and vertical
directions whereas high shape factor bearings,
characterized by values of S
F
greater than 20, only
provide a good isolation in the horizontal direction.
It is even obvious that low values of the shape factor
define thick rubber layers and, hence, provide
bearings characterized by high deformability. As a
rule, in seismic isolation applications the need to
have a device with a high vertical stiffness and low
shear stiffness requires that S assumes values greater
than 5 and less than 30.
Figure 3: Isolator vertical elastic modulus varying shape
factor and rubber hardness.
Three geometric cases corresponding to shape
factors S
F
equal to 7, 15 and 30 are hereafter
considered. In these cases, the thicknesses of the
single pad are approximately respectively equal to 5,
8.5 and 18 mm, assuming a width of the isolator
equal to 500 mm (square isolators) and a total
thickness equal to 250 mm. Assuming in the first
case a thickness of steel laminas equal to 1 mm, in
the second 2 mm and in the third 3 mm, the number
of steel plates to be used on such devices is
respectively equal to 38, 19 and 9.
Three refined discretizations are adopted in the
numerical simulations discussed in this Section, as
depicted in Figure 2. For rubber, eight-noded bricks
elements are used, whereas for steel laminas four-
noded plate and shell elements are adopted, to
properly take into account both the in-plane and the
out-of-plane effect induced by steel bending.
Obviously, the isolator with shape factor S=30
requires several elements, due to the reduced
thickness of the pads, namely 12224 bricks, 5328
plates and 14501 nodes.
Elastic analyses under small deformations are
performed to characterize the vertical elastic
modulus in compression, which is represented in
Figure 3, at different values of the shape factor
and for the three blends represented in
Figure 1 with
squares.
5 10 15 20 25 30
0
2000
4000
6000
8000
10000
12000
14000
16000
First shape factor
E
eq
[MPa]
Soft
Medium
Hard
SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
20

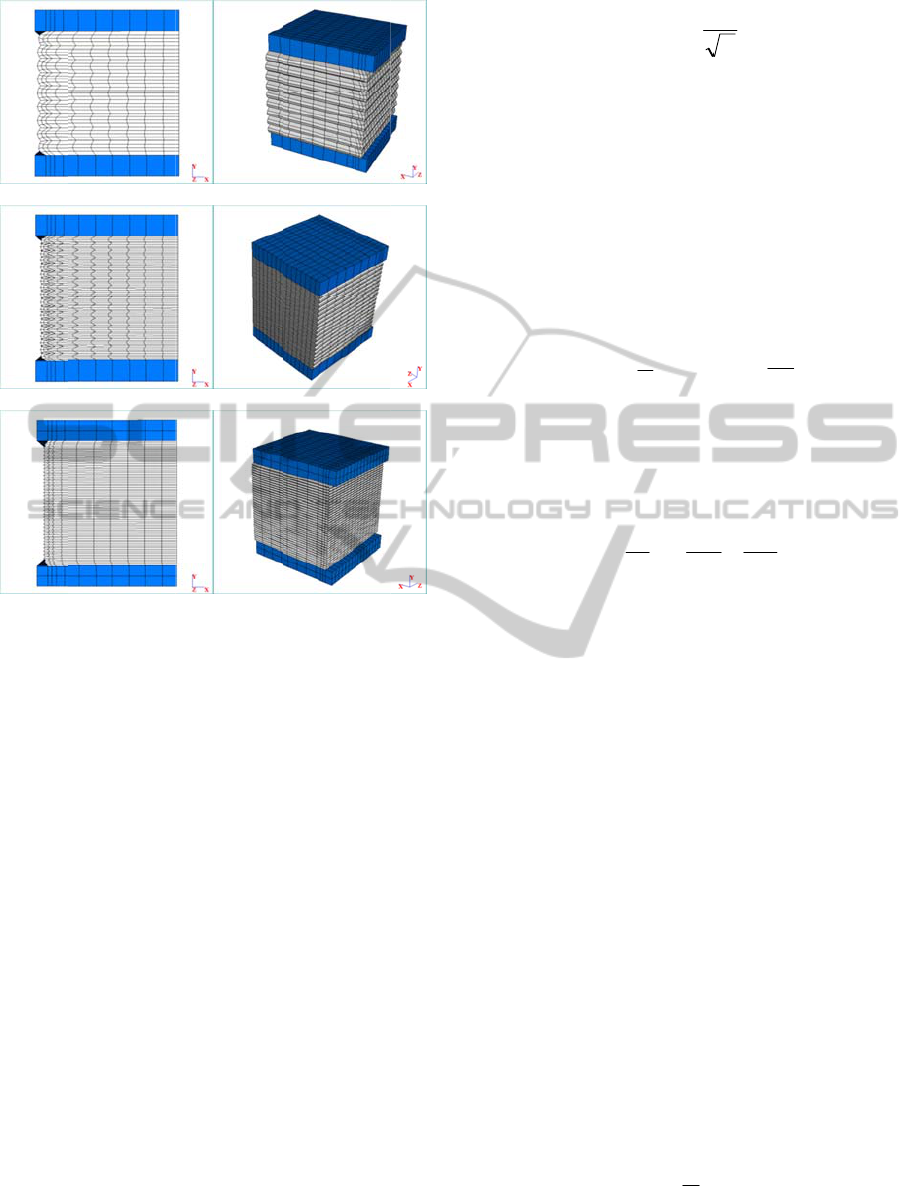
Figure
Obv
i
factor a
n
elastic
m
b
etween
shape f
a
should
b
soft bl
e
p
rogress
lower s
h
In
F
isolators
role pla
y
p
articul
a
To
s
under la
r
Rivlin
m
Defi
n
length i
n
length i
n
stretch i
n
corresp
o
stresses
32
= σσ
incompr
e
4: Deformed s
h
i
ously elastic
n
d is maximu
m
oduli of a
1500 and 7
5
a
ctor equal to
b
e used. Con
v
e
nds could
h
ively decreas
e
h
ape factors h
a
F
igure 4, d
e
under vertic
a
y
ed by the si
n
a
rly evident.
s
tudy the sh
e
r
ge deformat
i
m
odel is utiliz
e
n
ed the stre
t
n
the deform
e
n
the undefo
r
n
the directio
n
o
nding stres
s
are zero, sin
c
0=
. For
e
ssibility con
d
h
apes for verti
c
modulus inc
r
m for the ha
r
seismic isol
a
5
00 MPa, m
e
15, a mediu
m
v
ersely, for hi
g
h
ave the b
e
e
vertical stif
f
a
rd blends are
e
formed sha
p
a
l compressi
o
n
gle rubber p
a
e
ar behaviou
r
i
ons, a two c
o
e
d in what fol
l
t
ch as the r
a
e
d configurati
o
r
med state, l
e
n
of elongati
o
s
. The othe
r
c
e no lateral
f
constancy
o
d
ition
321
λλλ
c
al compressio
n
r
eases with s
h
r
d blend. Usu
a
tor should r
a
e
aning that
f
m
or a soft b
g
her shape fa
c
e
neficial rol
e
f
ness, wherea
s
preferable.
p
es of the
t
n are shown.
a
d free to bul
g
r
of the isol
a
o
nstants Moo
n
l
ows.
a
tio between
o
n divided b
y
e
t
λλ =
1
be
o
n and
σ
σ =
1
r
two prin
c
f
orces are ap
p
o
f volume,
1=
gives:
n
s.
h
ape
u
ally,
a
nge
f
or a
b
lend
ctor,
e
to
s
for
t
hree
The
g
e is
a
tors
n
ey-
the
y
the
e
the
σ
the
c
ipal
p
lied
the
M
o
W
h
det
e
tes
t
hol
d
un
s
uni
a
de
n
uni
a
dis
p
p
ri
n
ax
e
gra
d
de
fo
as
for
ha
v
The strain
e
o
oney-Rivlin
m
=W
where
2
1
1
λ =I
h
ere
1
C
and
e
rmined for i
n
t
.
In uniaxial t
e
d
and therefo
r
λ
1
=I
The engine
e
s
trained area
a
xial tensile
t
n
sity as follo
w
⎜
⎝
⎛
= 12'S
In simple s
h
a
xial compr
e
p
lacement do
e
n
cipal stretch
e
s. Due to app
d
ient tensor
fo
rmation tens
⎢
⎢
⎢
⎣
⎡
=
00
10
1
γ
F
Consequentl
y
21
3== II
Cauchy stres
s
2
12
T =
γ
In pure she
v
e the followi
n
λλ
32
==
n
ergy functi
o
m
odel is:
()
3
21
+−
C
IC
2
3
2
2
2
1
λλ ++
an
d
2
C
are mat
e
n
stance by a
s
e
nsion or co
m
r
e:
λ
λ
2
2
+
1
=I
e
ring stress
o
f cross-sect
i
t
est may be
e
w
s:
⎜
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
−
1
3
1
I
W
λ
λ
h
ear deformat
e
ssion, the
e
s not coinci
d
e
s; rather it
i
l
ied shear str
a
F
and th
or
B
are de
s
⎥
⎥
⎥
⎦
⎤
1
0
0
⎢
⎢
⎢
⎣
⎡
=
1
B
y
, the strain i
n
2
γ
+
,
3
=I
s
becomes:
/[
1
IW +∂∂
γ
a
r deformati
o
n
g form:
1
1
3
2
1
=
=
=
λ
λ
λ
λ
λ
λ
1
o
n for a tw
o
()
3
12
−I
C
d
2
12
−
+=
λ
λ I
e
rial paramet
e
s
imple uniaxi
a
m
pression equ
a
2
1
2
λ
λ +
'S
(force
i
on) in the c
a
e
valuated fro
m
⎟
⎟
⎠
⎞
∂
∂
+
2
1
I
W
W
t
ion and diff
e
direction o
f
d
e with the di
r
involves a r
o
a
in
γ
, the de
f
h
e left Cau
c
s
cribed as:
+
100
0
1
0
1
2
γ
γγ
n
variants are
e
1
and the e
x
]/
2
IW ∂∂
o
n
p
rincipal
(7)
o
constats
(8)
2
3
2
2
−−
+ λ
λ
.
e
rs to be
a
l tension
a
tions (7)
(9)
per unit
a
se of an
m
energy
(10)
e
rently to
f
applied
r
ection of
o
tation of
f
ormation
hy-Green
⎥
⎥
⎥
⎦
⎤
0
0
(11)
e
xpressed
x
pression
(12)
stretches
(13)
ElastomericSeismicIsolatorsBehavioratDifferentPadsThickness
21

Consequently, the strain invariants are expressed
as
1/1
22
21
++== λλ II
and the expression for
Cauchy stress becomes:
()
⎟
⎠
⎞
⎜
⎝
⎛
−−−=− 1
1
212
2
2
2
13311
λ
λσσ
CC
()
⎟
⎠
⎞
⎜
⎝
⎛
−+−−=− 1
1
212
2
1
2
23322
λ
λσσ
CC
()
⎟
⎠
⎞
⎜
⎝
⎛
−+=−
2
2
212211
1
2
λ
λσσ
CC
(14)
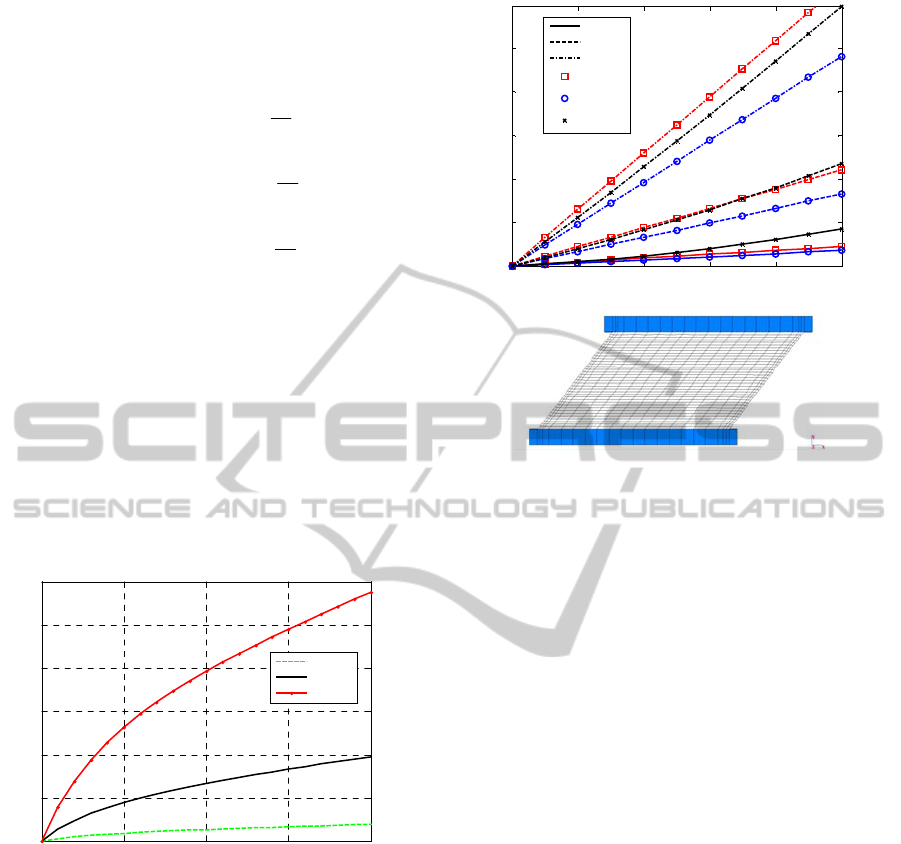
The normal behaviour under large deformations
of the single pad is shown in
Figure 5
. Such a response under large
deformations is fully determined once known the
two Mooney-Rivlin constants
1
C
and
2
C
. However,
the initial Young Modulus gives only one
information on such constants (G=2(
1
C
+
2
C
)). In
what follows we therefore assume
1
C
=G/2 and
2
C
=0, in absence of experimental data on constituent
materials, which corresponds to a Neo-Hookean
material.
Figure 5: Stretch-stress behaviour of a single rubber pad
(top) and pure shear behaviour under large deformations
(bottom).
Having at disposal
1
C
and
2
C
constants, a
standard large deformation software is utilized to
plot the response of the whole isolator in shear, as
sketched in Figure 6.
Figure 6
is particularly important for practical
purposes, because the curves may be implemented at
a structural level to study entire base-isolated
buildings in the dynamic range.
Figure 6: Force-displacement curves in shear under large
deformations and corresponding deformed shape (S=7).
As it is possible to notice, the utilization of
different hardness rubber pads in conjunction with
slender or less slender isolators may considerably
change the macroscopic response of the isolator and,
hence, the effectiveness of the device inserted in a
large case structure may be variable.
4 CONCLUSIONS
The important matter of the role played by the
thickness of rubber pads within seismic isolators is
not well covered in the literature. From our
theoretical investigation, it is shown that a proper
calculation is needed when the item involves a high
thickness and a large volume of the elastomer
compounds. Hardness is a very important parameter
to define rubber initial Young’s modulus, that is the
main parameter to define the possibility that a
predetermined thickness of the rubber pad is able to
suitably support the vertical load. As it is known, the
hardness determination, in general, is done on the
surface of the items and this is function, at same
recipe and rubber type, of the cross-link density. For
this reason it will be required to deepen such
preliminary results considering a particular rubber
type, an experimental recipe and a mathematical
approach to define the optimal vulcanization
time/temperature and subsequently link these
parameters with the hardness, to evaluate an optimal
1 1.5 2 2.5 3
0
10
20
30
40
50
60
Stretch
λ
[ ]
Engineering stress S' [MPa]
Soft
Medium
Hard
0 100 200 300 400 500
0
1000
2000
3000
4000
5000
Horizontal displacement [mm]
F shear force [kN]
Soft
Medium
Hard
S
F
=7
S
F
=15
S
F
=30
SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
22

cross-link density in any point of the items,
especially for isolators with big dimensions.
Another important parameter that will be
investigate is the hysteresis loss and thermo-
mechanical behavior that, as known, can be
correlated to the dynamic behavior based on cross-
link structures. Finally, it will be considered the
aging or the stability of the rubber items, that in
general depends on the structure of the elastomer
used. In our theoretical work it is shown that a
proper calculation is needed when a product
involves a large volume of the rubber items in the
seismic isolators. It is suggested to consider the
following steps for a choice of the optimal thickness
of the pads as a function of predetermined hardness,
which also allows to increase the volume of rubber
and decrease the number of the steel plates:
1) Calculation of the Young’s modulus from
hardness.
2) Calculation of the maximum vertical stiffness
supported.
3) Determination of the stretch-stress behaviour
of the single rubber pad.
4) Determination of the shear behaviour of the
whole isolator under large deformations.
5) Utilization of the stretch-stress and the shear
behaviour in order to define the best solution for a
single building.
6) Combination of the technical characteristics
of the rubber pads and the steel laminas to minimize
the cost, in order to introduce the seismic isolation
technology in large buildings in high seismicity
countries. The authors are convinced that this
approach could be in the future the normal routine to
design new buildings.
REFERENCES
Amin, A. F. M. S., Alam, M. S., Okui, Y., 2002. An
improved hyperelasticity relation in modeling
viscoelasicity response of natural and high damping
rubbers in compression: experiments, parameter
identification and numerical verification. Mech. Mater.
34: 74-95.
Amin, A. F. M. S., Wiraguna, I., Bhuiyan, A. R., Okui, Y.,
2006. Hyperelasticity Model for Finite Element
Analysis of Natural and High Damping Rubbers in
Compression and shear. Journal of Engineering
Mechanics ASCE, 132(1): 54-64.
British Standard 903, 1950, 1957. Methods of testing
vulcanized rubber, Part 19 (1950) and Part A7 (1957).
Gent, A. N., 1958. On the relation between indentation
hardness and Young’s modulus. Institution of Rubber
Industry – Transactions, 34: 46-57.
Gent, A. N., 1978. Rubber elasticity: basic concepts and
behavior. In: Science and Technology Rubber (Ed.: F.
R. Eirich), Academic Press, NY, San Francisco,
London.
Gracia, L. A., Liarte, E., Pelegay, J. L., Calvo, B., 2010.
Finite Element simulation of the hysteretic behavior
on industrial rubber. Application to design rubber
components. Finite Elements in Analysis and Design
46: 357-368.
Milani, G., Milani, F., 2012. Stretch-stress behavior of
elastomeric isolators with different rubber materials. A
numerical insight. Journal of Engineering Mechanics
ASCE, in press.
Moon, B. Y., Kanga, G. J., Kanga, B. S., Kim, G. S.,
Kelly, J. M., 2003. Mechanical properties of seismic
isolation system with fiber-reinforced bearing of strip
type. International Applied Mechanics, 39(10): 1231-
1239.
Moon, B. Y., Kanga, G. J., Kanga, B. S., Kim, G. S.,
Kelly, J. M., 2002. Design and manufacturing of fiber
reinforced elastomeric isolator for seismic isolation.
Journal of Materials Processing Technology, 130-131:
145-150.
Qi, H. J., Joyce, K., Boyce, M.C., 2003. Durometer
hardness and the stress-strain behavior of elastomeric
materials. Rubber Chemistry and Technology, 72(2):
419-435.
Studebaker, M. L., Beatty, J. R., 1978. The rubber
compound and its composition. In: Science and
Technology of Rubber (Ed.: F.R. Eirich), Academic
Press, NY, San Francisco, London.
Tobolsky, A. V., Mark, H. F., 1971. Polymer Science and
Materials. Chap.13 (Ed.: Wiley) New York.
Tsai, H. S., Kelly, J. M., 2002. Stiffness Analysis of Fiber-
Reinforced Rectangular Seismic Isolators. Journal of
Engineering Mechanics ASCE, 128(4): 462-470.
ElastomericSeismicIsolatorsBehavioratDifferentPadsThickness
23