
Dynamic Model of a 7-DOF Whole Arm Manipulator and Validation
from Experimental Data
Zaira Pineda Rico, Andrea Lecchini-Visintini and Rodrigo Quian Quiroga
Department of Engineering, University of Leicester, University Road, Leicester, U.K.
Keywords:
Whole Arm Manipulator Model, Friction Model, Friction Identification.
Abstract:
The present paper describes the design of the dynamic model of a 7 degrees of freedom whole arm manipulator
implemented in SimMechanics. The friction phenomena of the manipulator is identified, represented through
a fitted model and included in the system model with the aim of increment the accuracy of the model with
respect to the real system. The characteristics of the model make it suitable to test and design control strategies
for motion and friction compensation in MATLAB/Simulink.
1 INTRODUCTION
The computation of the dynamic model of a robot ma-
nipulator plays an important role in simulation of mo-
tion, analysis of the manipulator’s structure and de-
sign of optimal control algorithms. The inclusion of
the effects of friction in a mechanical system model
when simulating control strategies, helps to improve
the performance of the controller to be implemented
in the real system (Kostic et al., 2004; Indri, 2006;
Bompos et al., 2007). Most of the whole arm manip-
ulators mathematical models are based in the com-
putation of multi-links serial robot’s mathematical
equations. These equations are obtained using the
Newton-Euler recursive method to calculate the Cori-
olis, centrifugal and inertial forces observed when the
end-effector is in motion. Moreover, a Jacobian ap-
proach may be implemented in parallel for mapping
between Cartesian and joint space, in order to mini-
mize singularity conditions that increase the computa-
tion load of the control algorithm (Lau and Wai, 2002;
Sousa et al., 2009). This methodology involves both
operational and joint forces.
In most cases these mathematical models are
implemented using high level computing languages
as MATLAB (Corke, 1996), C/C++ or Fortran.
Nevertheless, in order to avoid significant com-
putation time, some authors have found in MAT-
LAB/SimMechanics a comfortable tool to design me-
chanical systems used for experimental verification.
The capability of this tool yields appropriate results
when working with joints with 1 DOF and when
all the manipulator’s inertial parameters are known
(MathWorks, 2011).
Section 2 offers a brief description of the real ma-
nipulator system. Section 3 gives insights on the de-
sign of the model and shows the importance of exper-
imental data in the development of the friction model.
In Section 4 the response of the real system is com-
pared to that of the model when simulating some ex-
periments. Finally, section 5 presents some conclu-
sions related to this work.
2 THE REAL SYSTEM
The real system is a 7-degrees-of-freedom whole arm
manipulator (WAM) from Barrett Technology Inc. It
is a joint torque controlled manipulator equipped with
configurable PD/PID control and gravity compensa-
tion. The information related to the joints configu-
ration, joint motor drives and the body part masses,
centre of gravity and inertia matrix is provided by the
manufacturer in the WAM ARM User’s Manual (Bar-
rett Technology Inc, 2008). Figure 1 shows the con-
figuration and attached frames of the 7-DOF system
with a grasper. All the joints of the manipulator are
1 DOF revolute joints. An image of the real system
is shown in Figure 2, consisting in a Barret 7-DOF
Whole Arm Manipulator with an attached BH8-series
BarrettHand.
For the developmentofthis projectthe 7-DOF ma-
nipulator is configuredwithjoint PD control and grav-
ity compensation given by Equation (1), where the
joint torque τ is expressed as the sum of the difference
217
Pineda Rico Z., Lecchini-Visintini A. and Quian Quiroga R..
Dynamic Model of a 7-DOF Whole Arm Manipulator and Validation from Experimental Data.
DOI: 10.5220/0004013002170222
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 217-222
ISBN: 978-989-8565-22-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Z4
X3,X4
Z3
J4
J1,J3
Z0,Z2
X0,X1,X2
Z1
J2
Zbase
Xbase
Xtool
Ztool
X5,X6
X7
J5,J7
Z6,Z7
Z5
J6
Figure 1: WAM 7-DOF Denavit-Hartenberg architecture
with attached frames as shown in (Barrett Technology Inc,
2008).
Figure 2: The Barret 7-DOF Whole Arm Manipulator with
the BH8-series BarrettHand.
between the reference and measured position, namely
position error ˜q, multiplied by a constant proportional
gain K
P
, the derivative of the error
˙
˜q multiplied by a
respective derivative gain K
D
and the compensation
for gravity g, which is a function of the joint position.
τ = K
P
˜q+ K
D
˙
˜q+ g (1)
The WAM joint PD control block diagram is shown
in Figure 3. The control loop uses the reference sig-
nal r(t), namely a joint trajectory, and the measured
position y(t) to compute the present error. Then the
derivative of the error is calculated, and the gravity
compensation is added to conform the joint torque
u(t) to be applied to the manipulator’s joint.
_
+
lIr(t)
lIy(t)
P
+
lu(t)
K
P
Ks
D
+
+
I
I
g( )y(t)
+
ie(t)
Figure 3: Configuration of the joint PD control with grav-
ity compensation. r(t) is the reference trajectory, e(t) is
the response error, P represents the manipulator, g(y(t)) is
the gravity compensation, K
D
and K
P
are the derivative and
proportional gains, respectively.
3 THE MODEL
The 7-DOF WAM model is built by four blocks:
• Seven modules that compute the joint reference
trajectories.
• The dynamic model of the system.
• Fitted friction models for each joint of the manip-
ulator.
• Joint PD controllers configured and tuned as those
implemented in the real system.
The dynamic model of the manipulator is based on
the configuration and physical characteristics of the
real system, the parameters of the friction model are
determined through the identification of the joint fric-
tions whilst the joint trajectory and joint controller are
emulations of those existent on the real system.
3.1 Trajectory Generation
The reference signal used to perform every joint ro-
tation is a linear segment parabolic blend (LSPB) tra-
jectory defined as follows. Up to a time t
c
the trajec-
tory is parabolic with linear velocity, at tc the trajec-
tory chances to linear with constant velocity and zero
acceleration, finally after a time (t
f
− t
c
) the trajec-
tory changes to parabolic again and the velocity de-
creases linearly until reaching zero. The motion pro-
duced when applying this velocity profile to any joint
is translated in a rotation from the initial joint posi-
tion q
i
of the manipulator to q
f
radians. Equation (2)
defines the described trajectory, where q
i
is the initial
position, q
f
is the final position reached in a time t
f
,
˙q
c
= ¨q
c
t
c
is the value of the constant velocity exhib-
ited from time t
c
to time (t
f
− t
c
) and ¨q
c
is the value
of the desired constant acceleration.
q(t) =
q
i
+
1
2
¨q
c
t
2
0 ≤ t ≤ t
c
1
2
(q
f
+ q
i
− ˙q
c
t
f
) + ˙q
c
t t
c
< t ≤ t
f
−t
c
q
f
−
1
2
¨q
c
(t
f
−t)
2
t
f
−t
c
< t ≤ t
f
(2)
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
218

0 1 2 3 4 5 6 7
-0.6
-0.4
-0.2
0
[rad]
[s]
Position
0 1 2 3 4 5 6 7
0
0.05
0.1
[s]
Velocity
0 1 2 3 4 5 6 7
-0.1
0
0.1
[rad/s
2
]
[s]
Acceleration
[ rad/s]
l
Figure 4: Example of a trapezoidal velocity profile when
the values of the variables are set as follows q
i
= −0.55,
q
f
= −0.05 rads, ¨q
c
= 0.083 rads/s, t
f
= 7s and t
c
= 1.
An example of the trajectory given by Equation (2)
can be seen in Figure 4 where a rotation of 0.5 rads is
performed.
In order to generate the LSPB joint trajectory, the
real system sets the value of the time of change tc as
1, and the velocity ˙q
c
and acceleration ¨q
c
are calculated
using Equations (3) and (4), taking into account the mea-
sured values of the initial and the final joint position q
i
and q
f
.
In simulations, the joint trajectory is emulated by the
model considering the experimental values of the initial
joint position q
i
, the final joint position q
f
and the exe-
cution time t
f
. The value of t
c
is set as 1 and the velocity
and acceleration are also calculated using Equations (3)
and (4). Finally, taking all the parameters previously es-
timated, the joint trajectory is generated using Equation
(2).
˙q
c
=
4(q
f
− q
i
)
t
2
f
− (−2(t
c
− 0.5t
f
))
2
(3)
¨q
c
= ˙q
c
(4)
3.2 The Dynamic Model
The dynamic model equation for a robot manipulator is
generally written in the form (Siciliano et al., 2009):
B(q) ¨q+C(q, ˙q) ˙q+ G(q) + F = τ (5)
where q, ˙q, ¨q are the position, velocity and acceleration
vectors of all the joints that shape the manipulator, B(q)
is the inertial matrix, C(q, ˙q) ˙q is the Coriolis-Centrifugal
matrix, G(q) is the gravity vector and F is the vector of
friction, which is usually obtained using a fitted friction
model.
The dynamic model of the WAM Arm was designed
and simulated using MATLAB/SimMechanics, and most
of the inertial data provided by the manufacturer had to
be adapted according to the inertial reference system.
The MATLAB/SimMechanics toolbox is a block dia-
gram modelling environment like Simulink, created by
MATLAB, to design and simulate mechanical systems.
The toolbox contains several modules that represent par-
ticular bodies and which inertial properties can be spec-
ified by the user.
A great advantage of using SimMechanics in mod-
elling mechanical systems is that the toolbox is prompt
to be used with Simulink so that control routines can be
added with ease in order to analyse the behaviour of the
system’s dynamics under motion constraints.
700 800 900
-1
-0.5
0
0.5
1
1.5
2
DataforfrictionmodellingJ1
Position[rads]
Samples(T=0.01s)
0 50 100 150 200 250 300 350 400
0.3
0.32
0.34
0.36
0.38
0.4
Samples(T=0.01s)
.Id
_
.idt
0 100 200 300 400 500
1
2
3
4
5
6
Torque[Nm]
4
4.5
5
5.5
6
Samples(T=0.01s)
0 100 200 300 400 500
Velocity[rad/s]
0 50 100 150 200 250 300 350 400
Samples(T=0.01s)
Torque[Nm]
Figure 5: Register of position and torque in the Barret WAM
when rotating joint 1 by 0.5 rads.
3.3 The Friction Model
Friction phenomena in robot manipulators may affects
the accuracy of the system in position control and when
moving the manipulator at very low velocities. Most
of the friction models employed when modelling posi-
tion controlled mechanisms, include several components
as the sliding friction (or Coulomb friction), the break-
down friction (or stiction) and the viscous friction (Bona
and Indri, 2005). In most cases if the manipulator is ex-
pected to displace at medium or medium-high velocities,
the friction can be expressed mathematically as a func-
tion of the joint velocity considering the effects of the
viscous friction and the Coulomb friction only (Guran
et al., 2001; Lewis et al., 2004; Kelly et al., 2005; Si-
ciliano et al., 2009). This simplified friction model is
known as classic friction model:
F = F
c
sign(v) + σ
2
v (6)
where F
c
in the parameter for Coulomb friction, σ
2
is
the viscous damping coefficient and v is the velocity of
the system. The value of the parameters for the classic
friction model can be estimated from experimental data
DynamicModelofa7-DOFWholeArmManipulatorandValidationfromExperimentalData
219
Friction[Nm]
Velocity[rad/s]
Friction-VelocityMapofJoint1
Friction-VelocityMapofJoint5
-0.4
-0.3
-0.2
-0.1
0
0.1 0.2 0.3
0.4
-0.4
-0.3
-0.2
-0.1
0
0.1 0.2 0.3
0.4
Velocity[rad/s]
Friction[Nm]
Friction[Nm]
Friction[Nm]
-4
-2
0
2
4
6
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.4
Velocity[rad/s]
0.8
0.4
Friction-VelocityMapofJoint2
Friction-VelocityMapofJoint6
Velocity[rad/s]
-0.4
-0.3
-0.2
-0.1
0
0.1 0.2 0.3
0.4
-0.4
-0.3
-0.2
-0.1
0
0.1 0.2 0.3
0.4
F
riction[Nm]
Friction[Nm]
-3
-2
-1
0
1
2
3
4
5
0
Velocity[rad/s]
Friction-VelocityMapofJoint3 Friction-VelocityMapofJoint4
Friction-VelocityMapofJoint7
-0.4
-0.3
-0.2
-0.1
0
0.1 0.2 0.3
0.4
-0.4
-0.3
-0.2
-0.1
0
0.1 0.2 0.3
0.4
-0.4
-0.3
-0.2
-0.1
0
0.1 0.2 0.3
0.4
Velocity[rad/s]
Velocity[rad/s]
Friction[Nm]
2
1
0
-1
-2
-3
2
1
0
-1
-0.4
-0.2
0
0.2
0.4
Measureddata
Estimation
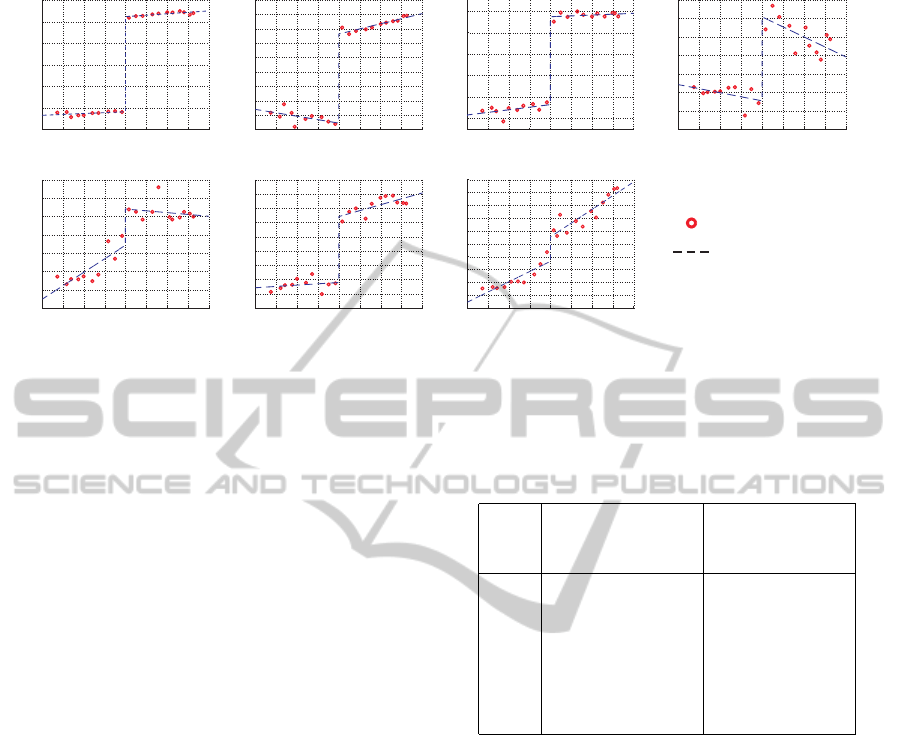
Figure 6: Friction velocity maps corresponding to each joint of the 7 DOF manipulator. The measured data is obtained after
rotating each joint of the manipulator at different constant velocities whilst the estimated value is computed using a fitted
classic friction model.
through the execution of joint rotations at constant veloc-
ity, this process in not straight forward and is explained
in detail in section 3.3.1.
3.3.1 Friction Identification
The procedure for the identification of the friction model
parameters for each joint of the 7-DOF whole arm ma-
nipulator follows several steps. First a closed loop PD
control with gravity compensation is used to move the
link following a trapezoidal velocity profile at different
positive and negative velocities, the measurements of po-
sition in addition with the corresponding sampling time
are employed to compute the velocity of the link in each
experiment. Afterwards, the values of torque and veloc-
ity during the constant velocity stage of the trajectory are
averaged and used to construct the friction-velocity map,
which is basically a torque versus velocity plot. Finally,
the parameters for the friction model are estimated to
fit the friction-velocity map by applying a least-squares
minimization method (Canudas de Wit and Lischinsky,
1997; Canudas de Wit et al., 1995; Olsson et al., 1998;
Johnson and Lorenz, 1992) using
n
∑
i=1
[F(v
i
) −
ˆ
F(v
i
)]
2
(7)
where F(v
i
) is the measured torque at certain velocity
v
i
(i.e the friction force), and
ˆ
F(v
i
) is the value com-
puted by the friction model represented in Equation (6).
Figure 5 shows an example of the measured position and
torque in the manipulator when rotating joint 1. The data
segment in the inset of the figure corresponds to the lin-
ear change in the position which is used to compute the
joint velocity. The averages of the computed velocity v
i
and measured torque F(v
i
), respectively, yield to ordered
pairs [F(v
i
),v
i
] that shape the friction velocity map.
The obtained friction model parameters for each
Table 1: Friction model parameters for the seven joints of
the robot manipulator. V +/V− stands for positive and neg-
ative velocities respectively.
Joint Coulomb friction Viscous friction
F
c
σ
2
(V + /V−) (V + /V−)
1 4.4748/ 4.3609 1.3348/ 0.8266
2 2.6385/ 3.5643 3.5572/-2.3951
3 1.7399/ 2.3529 0.3944/ 1.2075
4 1.5414/ 0.7342 -2.7045/-1.0969
5 0.2798/ 0.1172 -0.1972/ 1.4670
6 0.4834/ 0.4417 0.8291/ 0.1836
7 0.0538/ 0.1370 1.0689/ 0.7954
joint of the 7-DOF whole arm manipulator are listed in
Table 1. There can be noted that the first joint is the
most affected by the Coulomb friction F
c
whilst the 3
DOF that shape the wrist of the manipulator are the least
influenced. These parameters were used to estimate the
joint friction velocity maps plotted in Figure 6, where the
velocity maps obtained using real data are also shown.
The measured friction suited perfectly the shape of
the classic friction model, which reinforces the initial
choice of the friction model for the development of this
project. In general, the estimation of friction is very ac-
curate for all the joints, and it is suitable enough to be
considered when compensating the friction phenomena
manifested in the real manipulator.
4 SIMULATIONS
Several joint rotational motion experiments were per-
formed with the aim of evaluate the accuracy of model
with respect to the real manipulator. First, a LSPB joint
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
220
Manipulator
Model
ix10
-3
0
2
4
6
5
3
1
Joint1
P
ositionError[rads]
Time[sec]
10
12
18
16
Joint2
PositionError[rads]
2
4
6
PositionError[rads]
Joint3
PositionError[rads]
Joint4
0
2
4
6
8
PositionError[rads]
Joint5
P
ositionError[rads]
Joint6
0
10
20
30
40
PositionError[rads]
Joint7
Time[sec] Time[sec] Time[sec]
Time[sec] Time[sec]
Time[sec]
7
14
8
6
2
4
1
3
5
4
3
2
1
1
3
5
7
2
4
6
8
10
12
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
ix10
-3
ix10
-3
ix10
-3
ix10
-3
ix10
-3
ix10
-4
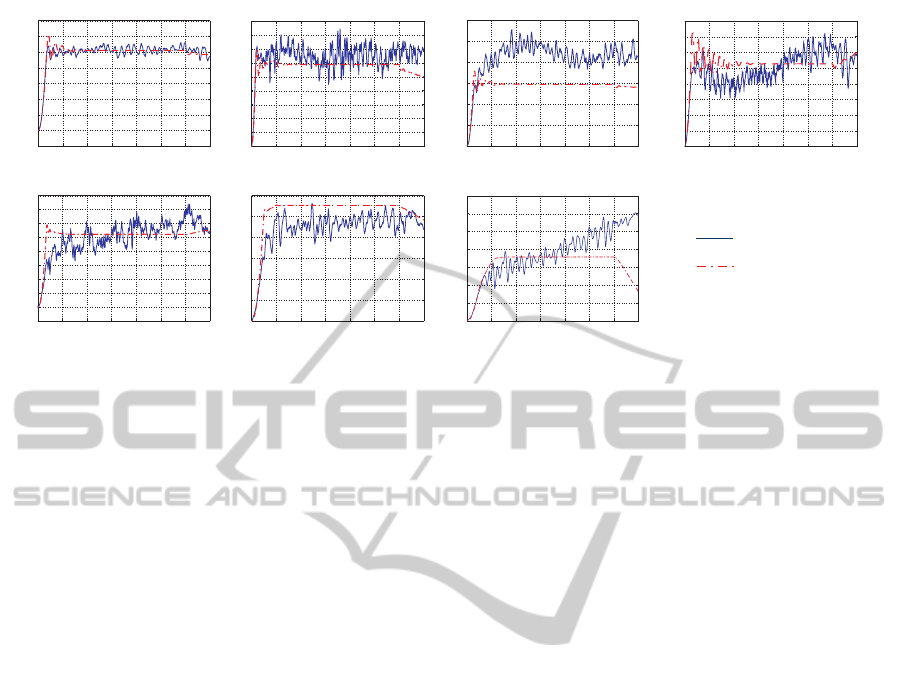
Figure 7: Real and simulated joint error of the 7 DOF manipulator when executing a specific trajectory. Every link is rotated
one at a time and the error is calculated using the reference position minus the actual position.
trajectory with a rotation of 0.5 rad at a velocity of 0.083
rads/sec was used as a reference in the real system, and
the joint position was measured while the manipulator
was in motion. Subsequently, the joint position error
was calculated to be used as a performance measure-
ment. Later, in simulation, the same joint trajectory was
generated using experimental data as described in Sec-
tion 3.1. The response of the model was recorded and
the model joint position error was calculated.
The position error was chosen as a performance mea-
surement in order to have a closer comparison of the re-
sponse of both the real manipulator and the model when
executing the exact same trajectory. As mentioned ear-
lier, the real system uses a PD control with gravity com-
pensation, and therefore, throughout the simulations a
PD control was used and zero gravity was assumed.
During the first set of simulations every link was ro-
tated one at a time. The second set consisted in one simu-
lation only, where all the joints were rotated at the same
time. This gave a total of eight simulations performed
by the model, to be compared to the behaviour of the
real system when executing the exact same trajectory.
The graphs in Figure 7 show a comparison of the posi-
tion error obtained in the first set of simulations. This
practice helped to prove the veracity of the model with
friction joint per joint and showed that, regardless of the
real manipulator is exposed to transducer noise and sen-
sor errors, the response of the model is accurate.
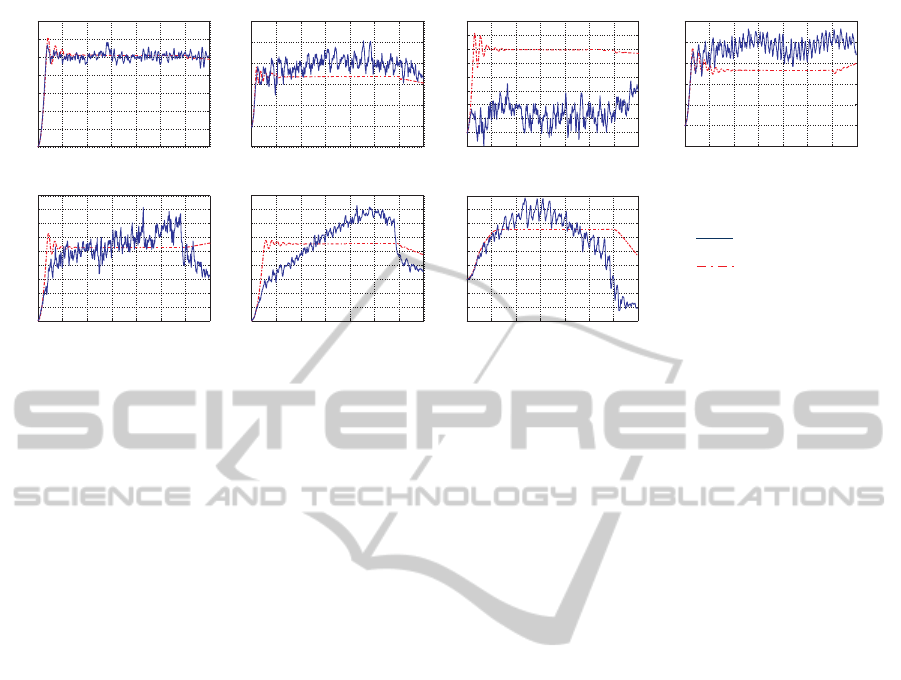
The second set of simulations was more an evalua-
tion of reliability, due to in real exercise the manipulator
might operate in Cartesian space and all the joints would
rotate at the same time. The response of the model dur-
ing this simulation was good as expected despite of the
clear difference between the simulated and the real po-
sition error of the third joint. Figure 8 shows the results
of the second set of simulations. The difference in errors
between model and real system are expected due to the
disturbances at which the real system is exposed, such as
nonlinearities caused by the joint motors and the inertia
of the system. Other sources of disturbance to be con-
sidered are the joint actuators and the scheme used for
gravity compensation.
5 CONCLUSIONS
The identification of friction phenomena in the manip-
ulator is helpful to observe the effects that friction has
in the overall performance of the system, so a compen-
sation technique, if necessary according to the applica-
tion task of the manipulator, may be implemented on the
current joint PD/PID control. On the other hand, the in-
clusion of a friction model in the dynamic model of the
mechanical system establish a good platform for simu-
lations in order to observe and analyse the response of
the manipulator to different control strategies in a more
realistic scenario.
The presented dynamic model with friction is prompt
to be used as a reference in the design of joint control
strategies implemented in Simulink. By taking advan-
tage of the fact that real joint trajectory is completely
emulated in our simulations by setting up the desired ro-
tation angle and execution time, a close comparison of
the simulation results with respect to experimental data
is also possible.
The development of a dynamic model with friction
is extremely useful for observing and improving the per-
formance of the manipulator by analysing the effective-
ness of the on system control. In certain cases, some
types of stimuli utilised in controller tuning techniques
are not feasible to be implemented in experiments whilst
the model can be easily manipulated in simulations.
DynamicModelofa7-DOFWholeArmManipulatorandValidationfromExperimentalData
221
2
4
6
5
3
1
2
4
2
4
6
8
-10
10
20
30
7
1
3
4
3
2
1
1
3
5
7
2
4
6
8
10
18
25
20
15
10
5
0
0
5
0
9
12
14
16
0
25
15
5
-5
Manipulator
Model
ix10
-3
Joint1
P
ositionError[rads]
Time[sec]
Joint2
PositionError[rads]
PositionError[rads]
Joint3
PositionError[rads]
Joint4
PositionError[rads]
Joint5
P
ositionError[rads]
Joint6
PositionError[rads]
Joint7
Time[sec] Time[sec] Time[sec]
Time[sec] Time[sec]
Time[sec]
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
0
ix10
-3
ix10
-3
ix10
-3
ix10
-3
ix10
-3
ix10
-4
Figure 8: Real and simulated joint error of the 7 DOF manipulator when executing a specific trajectory. All the joints are
rotating at the same time and the error is calculated using the reference position minus the actual position.
REFERENCES
Barrett Technology Inc (2008). WAM Arm User's Manual.
Bompos, N., Artemiadis, P., Oikonomopoulos, A., and Kyr-
iakopoulos, K. (2007). Modeling, full identification
and control of the mitsubishi pa-10 robot arm. In
IEEE/ASME International Conference on Advanced
Intelligent Mechatronics,.
Bona, B. and Indri, M. (2005). Friction compensation in
robotics: an overview. In 44th IEEE Conference on
Decision and Control.
Canudas de Wit, C. and Lischinsky, P. (1997). Adaptive
friction compensation with partially known dynamic
friction model. In International Journal of Adaptive
Control and Signal Processing.
Canudas de Wit, C., Olsson, H., Astrom, K., and Lishinsky,
P. (1995). A new model for control of systems with
friction. In IEEE Transactions On Automatic Control.
Corke, P. (1996). A robotics toolbox for matlab. In IEEE
Robotics and Automation Magazine.
Guran, A., Pfeiffer, F., and Popp, K. (2001). Dynamics with
friction. In Series on Stability, Vibration and Control
of systems.
Indri, M. (2006). Control of manipulators subject to un-
known friction. In 45th IEEE Conference on Decision
and Control.
Johnson, C. and Lorenz, R. (1992). Experimental identifi-
cation of friction and its compensation in precise, po-
sition controlled mechanisms. In IEEE Transactions
on Industry and Applications.
Kelly, R., Santibanez, V., and Loria, A. (2005). Control of
Robot Manipulators in Joint Space. Springer.
Kostic, D., de Jager, B., Steinbuch, M., and Hensen, R.
(2004). Modeling and identification for high perfor-
mance robot control: An rrr-robotic arm case study.
In IEEE Transactions on Control System Technology.
Lau, H. and Wai, L. (2002). A jacobian-based redun-
dant control strategy for the 7-DOF WAM. In Sev-
enth International Conference on Control, Automa-
tion, Robotics and Vision.
Lewis, F., Dawson, D., and Abdallah, C. (2004). Robot
Manipulator Control: Theory and Practice. Marcel
Dekker, second edition.
MathWorks (2011). MATLAB/SimMechanics.
Olsson, H., Astrom, K., Canudas de Wit, C., Gafvert, M.,
and Lischinsky, P. (1998). Friction models and friction
compensation. In European Journal of Control.
Siciliano, B., Sciavicco, L., Villani, L., and Oriolo, G.
(2009). Robotics: Modelling, Planning and Control.
Springer, London.
Sousa, C., Cortesao, R., and Queiros, P. (2009). Compli-
ant co-manipulation control for medical robotics. In
Proceedings of the 2nd Conference on Human System
Interactions.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
222
