
Simulation and Multi-objective Optimization
of Vaccuum Ethanol Fermentation
Jules Thibault
1
, Rubens Maciel Filho
2,3
, Marina O. S. Dias
3
, Tassia L. Junqueira
2,3
, Otavio Cavalett
3
Charles D.F. Jesus
3
, Carlos E.V. Rossell
3
and Antonio Bonomi
3
1
Department of Chemical and Biological Engineering, University of Ottawa, Ottawa (Ontario), K1N 6N5, Canada
2
Faculdade de Engenharia Química, Departamento de Processos Químicos
Universidade Estadual de Campinas, R. Albert Einstein, nº 500,13081-970 - Campinas, SP - Brazil
3
Laboratório Nacional de Ciência e Tecnologia do Bioetanol - CTBE/CNPEM
Caixa Postal 617013083-970, Campinas, Brazil
Keywords: Ethanol Fermentation, in Situ Recovery, Vacuum Fermentation, Simulation, Optimization.
Abstract: With the overall objective of optimizing an integrated first and second generation bioethanol production
plant, a simple illustrative example is first used to examine the advantages and challenges of using a
combination of VBA and UniSim Design for multi-objective optimization. In this paper, the simulation and
optimization of a vacuum fermentation system using glucose and xylose as substrates is performed. The
simulation of the fermentation system and the optimization are performed in the VBA environment, while
UniSim Design is used to provide thermodynamic data necessary to perform calculations and used to
simulate the downstream portion of the fermentation vacuum system. The Pareto domain of the system was
circumscribed based on three decision variables (starting time of vacuum, rate of broth removal by vacuum
and condenser temperature) and four objective functions (minimum ethanol loss, maximum productivity,
minimum residual sugars and minimum compression energy). The procedure developed has allowed to
easily circumscribe the Pareto domain of this system and to observe clearly the compromises that are
required when all objective functions are optimized simultaneously. Some challenges to overcome are the
time required for exchanging information between VBA and UniSim Design and the risk of non-converging
for complex problems. For this procedure to be implemented effectively for the integrated ethanol plant,
some innovative measures need to be developed.
1 INTRODUCTION
As a mean of partially reducing the world
dependence on non-renewable petroleum as a fuel
source and overall carbon dioxide emissions,
research on biofuels has intensified significantly
during the last decade with the main focus placed on
bioethanol and biodiesel, and more recently on
biobutanol. In many industrialized countries, over
two thirds of the refined petroleum products sold is
used for transportation purposes (NRCan, 2009; U.S.
EIA, 2010). This includes gasoline, low-sulphur
diesel, and aviation fuel. There is therefore a need
for a transitional fuel that will allow for a smooth
changeover.
Bioethanol has great potential and has already
been blended with some mainstream fuel sources at
concentrations varying from 10% per volume up to
100%. Bioethanol has many advantages, including
reduced dependence on imported oil, new markets
for farmers and foresters, and a reduction of
greenhouse gas (GHG) emissions from vehicles.
Facing with the highly-publicized criticism of
diverting farmlands or crops away from the human
food chain supply (not the case for sugarcane), a
shift to second-generation biofuels and a greater use
of residual lignocellulosic biomass to produce
biofuels is well underway to partly reduce this
controversy.
The step before fermentation, to obtain
fermentable sugars, and the microorganisms used in
fermentation are the main differences between the
ethanol production processes from simple sugar,
starch or lignocellulosic material (Mussatto et al.,
2010). The production of bioethanol from
lignocellulosic biomass is significantly more
79
Thibault J., Maciel Filho R., O. S. Dias M., L. Junqueira T., Cavalett O., D. F. Jesus C., E. V. Rossell C. and Bonomi A..
Simulation and Multi-Objective Optimization of Vaccuum Ethanol Fermentation.
DOI: 10.5220/0004014400790086
In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),
pages 79-86
ISBN: 978-989-8565-20-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
complex and costly than the one from sugarcane and
corn (Krissek, 2008). Indeed the efficient conversion
of lignocellulosic biomass into fermentable sugar
remains a major challenge for commercial
application (Margeot et al., 2009). The impetus
nowadays is to have a more integrated plant with the
production of multiple products. In Brazil, current
bioethanol plants draw their revenues from sugar,
bioethanol and electricity. In newer plants, first and
second generation bioethanol production will
probably be integrated, taking advantage of sharing
part of the infrastructure and the feedstock
availability (bagasse and trash) for second
generation ethanol production (Dias et al., 2012).
The increased complexity of these plants requires
the system to be well optimized.
A research project has been initiated to optimize
the integrated ethanol plant. The complete integrated
plant has been simulated using Aspen Plus (Dias et
al., 2008). It is desired to use this simulated plant to
perform a multi-objective optimization of this plant
by integrating it into an optimization algorithm.
Various scenarios are currently envisaged to
determine how to best incorporate the simulated
plant. One scenario, which is the subject of this
paper, is to use Excel/VBA (Visual Basic for
Applications) as an optimization platform but also as
a communication platform for passing on arguments
to and retrieving information from Aspen HYSYS or
Honeywell UniSim Design.
Given the complexity of the simulated ethanol
integrated plant, it was decided to implement this
scenario progressively. As a first step, it was desired,
via a simple illustrative example, to examine how
the combination of Excel, VBA and UniSim Design
could be used for optimizing a vacuum ethanol
fermentation process with regards to the protocol of
communication, the ease of convergence and the
time required to converge to an optimized solution.
In this paper, a vacuum fermentation system is
simulated and optimized based on three decision
variables and four objective criteria. The paper is
organized as follows. First, the simulated
fermentation system will be described followed by
the description of the optimization procedure. Some
results will then be presented and discussed prior to
concluding.
2 FERMENTATION SYSTEM
The simple illustrative process of Figure 1 consists
of a fermenter containing initially 500 m
3
of
inoculated fermentation medium. The initial
substrate concentrations of glucose and xylose in the
broth are 150 g/L and 75 g/L, respectively. A ratio
of 2:1 for glucose:xylose is typical of fermentable
sugars from lignocellulosic biomass. At this level of
substrate concentration, incomplete consumption
occurs because ethanol reaches a concentration level
that is completely inhibitory to the microorganism.
The in situ ethanol recovery from the fermentation
broth can partly mitigate product inhibition and
extend the fermentation, thereby allowing more
complete substrate utilization. Many methods have
been proposed to achieve this objective (Cardona
and Sanchez, 2007): liquid-liquid extraction (Jassal
et al., 2009), adsorption (Einicke et al., 1991), gas
stripping (Liu and Hsien-Wen, 1990), pervaporation
(Groot et al., 1992), and vacuum fermentation (Park
and Geng, 1992). In this investigation, a simplified
version of vacuum fermentation is simulated.
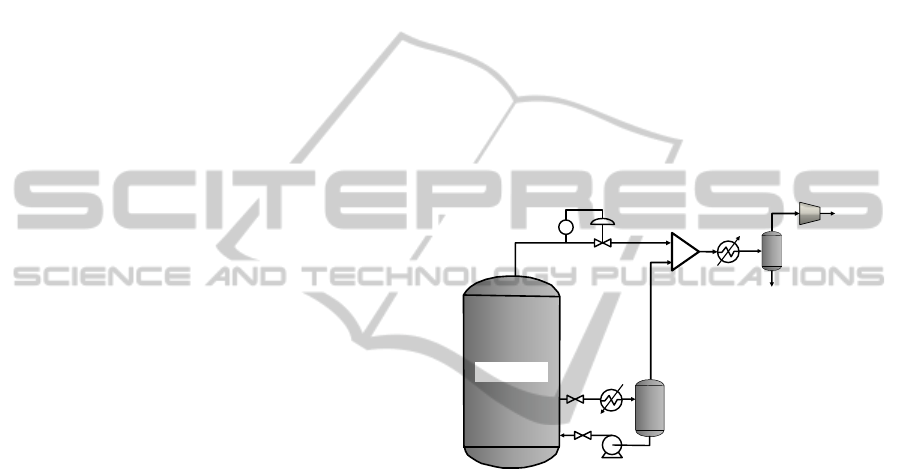
Figure 1: Simplified vacuum fermentation system.
The fermenter of Figure 1 operates at
atmospheric pressure but is equipped with an
external flash tank that, when in operation, is
maintained at a pressure low enough for the
fermentation broth to boil. When it is desired to
continuously remove a portion of ethanol from the
fermentation broth to reduce the inhibition, a small
stream of the fermentation broth is continuously
circulated through the external flash tank to be
partially evaporated. The heat exchanger preceding
the external flash tank serves to provide the latent
heat of vaporization of the evaporated fraction of the
stream and is used to control the rate of evaporation.
The exiting vapour is richer in ethanol such that the
in situ ethanol recovery is possible, resulting in a
decrease or a delay in fermentation inhibition caused
by ethanol accumulation. The exiting vapour passes
through a condenser to recover most of the
evaporated water and ethanol. In the present scheme,
in order to simplify the number of components, it
also was decided to send the CO
2
stream to the
PC
1
2
3
4
5
6
7
Fermenter
Flash
Tank
Compressor
Condenser
Heater
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
80
condenser in lieu of having a separate absorption
column.
2.1 Fermentation Model
There are numerous models for predicting the
production and consumption of the main species
involved in fermentation. In this investigation, the
model of Leksawasdi et al. (2001) was used. This
model was developed for the batch fermentation of
mixtures of glucose and xylose by recombinant
Zymomonas mobilis strain ZM4(pZB5), containing
additional genes for xylose assimilation and
metabolism. The model represented very well
experimental biomass growth, utilization of the two
substrates and ethanol production over a large range
of substrate concentrations.
This model has been adopted in this investigation
to evaluate the in situ product recovery during
fermentation operating at 30
o
C. The microbial
growth on each sugar is modelled using Equation (1)
with index j being 1 for glucose and 2 for xylose,
respectively. This equation includes three terms
affecting the maximum growth rate: (1) Monod
kinetics for substrate limitation, (2) ethanol
inhibition with a threshold level and a maximum
inhibitory concentration, and (3) a typical substrate
inhibition term.
iX,j iX,j
j
X,j max,j
X,j j mX, j iX,j iX,j j
P - P K
S
r = 1 -
K + S P - P K + S
S
(1)
The total biomass growth based on these two
sugars is represented by Equation (2).
X,1 X,2
dX
= r + (1 - )r X
dt
(2)
The associated glucose and xylose consumption
rates are given in Equation (3).
iS,j iS,j
jj
,max, j
SS,j j mS, j iS, j iS, j j
P - P K
dS S
= - 1- X
dt K +S P -P K +S
S
q
(3)
The rate of ethanol production can be related to
the rates of glucose and xylose consumption subject
to similar constraints and is given in Equation (4).
P,1 P,2
dP
= r + (1 - )r X
dt
(4)
with
iP,j iP,j
j
P,j ,max, j
SP,j j mP,j iP,j iP, j j
P - P K
S
r = 1 -
K + S P - P K + S
P
q
(5)
The model of Leksawasdi et al. (2001) did not
need to account for the production of carbon dioxide
during fermentation. However, in the present
investigation, it is necessary to know the amount of
carbon dioxide leaving the fermenter when vacuum
is used to reduce the concentration of ethanol in the
fermenter. We will assume that CO
2
is produced
according to stoichiometric equation for the
consumption of glucose and xylose. For each kg of
glucose or xylose consumed, 0.489 kg CO
2
is
produced. It is assumed that the same quantity of
CO
2
is produced whether the substrate is used for
ethanol production or biomass. It is therefore
possible to write the following differential equation
to account for the rate of CO
2
produced.
12
dS dS
dG
= - 0.489 +
dt dt dt
(6)
where dG/dt represents the mass rate of CO
2
production per unit volume of liquid broth.
The 31 parameters of the model can be found in
Leksawasdi et al. (2001). With these parameters and
the three sets of initial conditions given in the paper,
it was possible to reproduce exactly the curves
appearing in the publication.
2.2 Simulation Details
To perform the optimization of the process (covered
in the next section), the simulation of the complete
system must be performed numerous times with
different input design parameters. It is not possible
to perform the fermentation simulation within
UniSim Design such that the simulation of the
majority of the system and the optimization
algorithm were performed in the VBA environment
and UniSim Design was used as a supporting
platform for thermodynamic calculations and for
simulating the immediate downstream part of the
process. The simulation subroutine first obtains from
an EXCEL spreadsheet the initial conditions of the
fermenter content: X
0
(0.028 kg/m
3
), S
10
(150
kg/m
3
), S
20
(75 kg/m
3
), P
0
(0 kg/m
3
), fermentation
time (40 h) and the volume (500 m
3
). A schematic
diagram of the interaction between these computer
programs is presented in Figure 2.
Figure 2: Diagram of simulation communication protocol.
The fermentation is initiated in batch mode such
that the system of Equations (1)-(6) is integrated
numerically. An additional term in the mass
balances for the batch fermentation was added to
Excel UniSim
Object
Library
Object
Library
VBA
Simulation and Multi-Objective Optimization of Vaccuum Ethanol Fermentation
81

account for the entrainment of ethanol and water
from the fermenter due to carbon dioxide exiting the
fermenter. It is assumed that the carbon dioxide gas
stream leaves the fermenter saturated in ethanol and
water. When the external flash tank is put in
operation, an additional term to the mass balance of
each differential equation is added to account for the
evaporation rates of ethanol and water.
For each integration step of the mass balance
differential equations, the vapour partial pressure of
ethanol and water is calculated by passing to UniSim
Design the concentration of the fermentation broth
and by retrieving the equilibrium mass fraction in
the vapour phase (stream 1). With this information,
it is possible to perform a complete mass balance for
each species within the fermenter and to calculate
the mass flow rate and composition of streams 1 and
2 (Figure 1). The information of the combined
stream 3 and the desired exit temperature of stream 4
are then sent to UniSim to perform heat and mass
balances and to calculate the mass flow rates and
concentrations of streams 5, 6 and 7. VBA then
retrieves these flow rates and concentrations in
addition to the energy required for cooling stream 3
and the power required by the compressor. A
screenshot of the two simple systems used in
UniSim Design is shown in Figure 3.
Figure 3: UniSim Design screen capture showing the two
processes supporting VBA simulation.
3 OPTIMIZATION ALGORITHM
3.1 Multi-Objective Optimization
The first step to optimize a process is choosing a set
of process decision variables that can be
manipulated and that have an effect on a series of
objective functions. The choice of these decision
variables and objective functions need to be
performed by experts who have a profound
knowledge of the process. In the simple vacuum
fermentation illustrative example, three decision
variables were first considered (ranges of variation
in brackets): (1) the time at which the vacuum
system is placed in operation [0, 40 h], (2) the
evaporation rate in the external vacuum flash tank
[0, 6 m
3
/h], and (3) the exit temperature of the
condenser (stream 4) [-10, 10
o
C].
For this optimization study, four objective
functions were retained: (1) minimization of overall
ethanol lost (kg), i.e. the cumulative amount of
ethanol leaving stream 7, (2) maximization of
overall ethanol productivity (kg/m
3
h) based on
initial fermenter volume, (3) minimization of
residual sugars at the end of fermentation (kg), and
(4) minimization of the average consumption by the
compressor (MJ/h). This selection is of course not
unique and, ideally, the amortized total capital and
operating costs per kg of ethanol produced could
also need to be considered. However, to investigate
the benefits and constraints of using a combination
of EXCEL-VBA-UniSim Design, the current
example meets this requirement. As mentioned, this
simple example must be viewed as a preliminary
exploration for the optimization of the complete
integrated ethanol plant.
This problem, as summarized in Figure 4, is a
multi-objective optimization system. It is desired to
determine the values of the decision variables that
will maximize the second objective function while
minimizing the other three functions. It is possible to
combine the four objective functions into a single
profit function to be minimized. Even though single
objective optimization has been often used in the
literature, this method suffers from several
disadvantages such as the lack of information about
the trade-offs amongst various competing objectives,
the difficulty to assign the relative weighting to each
individual objective in a single profit function and
the convergence on a suboptimal point (local
maximum or minimum) instead of global optimum
in complex nonlinear problems (Deb, 2001; Haupt
and Haupt, 2004).
Even though it requires more computation time,
it is significantly more informative to solve the
problem as a multi-objective problem with the
distinct advantage to generate multiple Pareto-
optimal solutions that provide the decision maker or
expert a global perspective about trade-offs between
conflicting objectives. Other advantages include the
ability to optimize functions without requiring
information about function derivatives and therefore
application in non-convex, non-concave and
discontinuous problems (Deb, 2001; Haupt and
Haupt, 2004).
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
82

Figure 4: Schematic optimization block flow diagram of
the decision variables and objective functions.
3.2 Pareto Domain
The Pareto domain is the set of all feasible solutions
that are non-dominated by other solutions in that set.
A solution X
1
is said to dominate another solution X
2
if the values of all objectives for X
1
are not worse
than those of X
2
, and the value of at least one
objective for X
1
is better than the corresponding X
2
(Deb, 2001). Otherwise, both points are non-
dominated relative to each other.
Different algorithms exist in the literature to
circumscribe the Pareto domain from an initial
population of solutions. In this investigation, the
dual population evolutionary algorithm (DPEA) was
used. This algorithm incorporates the concepts of
domination to generate the Pareto domain. The
general approach is briefly described as follows
(Perrin et al., 1997; Thibault, 2008):
1. An initial set of decision variables is randomly
generated within their specified ranges. For each
of these points, the values of the objective
functions are then calculated as per Section 3.1.
2. The objective functions of all the points are
compared to the others (one solution versus
another at a time) to determine the number of
times a solution is dominated by another.
3. The non-dominated solutions of the population
and a portion of the least dominated solutions are
used to generate new solutions to replace
discarded solutions. To generate a new solution,
two kept solutions are chosen randomly and a
linear interpolation of their decision variables is
performed and the objective functions are
calculated.
4. The procedure is repeated until the desired
number of non-dominated individuals in the
population is obtained.
When the Pareto domain is circumscribed, it can
be used per se or the solutions can be ranked
according to some preferences expressed by an
expert. Two methods are particularly efficient to
capture preferences of experts: Net Flow Method
and Rough Set Method (Thibault, 2008). In this
investigation, only the Pareto domain will be
circumscribed and analyzed.
4 RESULTS AND DISCUSSION
4.1 Simulation Statistics
For each function call of the optimizing subroutine,
the set of mass balance equations for the
fermentation system was integrated over a period of
40 h with a time step of 0.1 h for a total 400
integration steps. Under ideal conditions, it takes
approximately 16 to 20 s of computation time to
simulate the 40 h fermentation on a Lenovo laptop
computer with an Intel 2.49GHz Dual Processor.
Sometimes it took much longer to complete a
simulation run. The difference in time required
undoubtedly depends on the ease to converge to a
solution within UniSim even though the flowsheet is
relatively simple. The majority of this time is spent
communicating with UniSim Design and performing
calculation within UniSim. Indeed, to perform a
complete function call without resorting to UniSim
took less than 1 s.
When the correct communication protocol has
been established between VBA and UniSim Design,
the simulation of a complete fermentation run was
possible and the optimization routine was able to
properly approximate the Pareto domain. To obtain a
population of 242 non-dominated solutions, it took
more than 1500 function calls. A higher number of
function calls are required when the number of
objective functions is higher. It requires significantly
more function calls than a traditional optimization
method but it is believed that the payback in having
the possibility to examine the trade-offs expressed
by the Pareto domain is all worth it.
The use of a metamodel is currently being
explored to converge more rapidly to the final Pareto
domain. In this method, a neural network model
representing the underlying relationship between the
decision variables and the objective functions would
be developed using the information of the initial
population. The metamodel would then be used in
the optimization method to determine the Pareto
domain. Finally, the Pareto domain obtained using
the metamodel would be validated and refined using
the more accurate original model. The development
of convergence promoter tools is important if one
wants to tackle the optimization of the complete
ethanol plant in the future. Other techniques are also
being evaluated.
4.2 Pareto Domain
A Pareto domain is specific to a set of decision
variables and objective functions. Changing some of
Vacuum
Fermentation
System
t
Vac
F
Out
T
4
Ethanol loss
Ethanol productivity
Residual sugars
Energy of compressor
Simulation and Multi-Objective Optimization of Vaccuum Ethanol Fermentation
83
the decision variables and/or objective functions will
lead to a different Pareto domain. All solutions
within the Pareto domain are non-dominated
solutions such that in the pairwise comparison of
any two solutions, each solution is better for at least
one objective function. All feasible solutions outside
the Pareto domain are dominated which means that
there exists at least one point within the Pareto
domain that is better for all four objective criteria.
The main advantage of the Pareto domain is the
possibility to clearly observe the compromises that
are being made when trying to optimize all four
objective functions at the same time. The resulting
Pareto domain is a four-dimensional surface
containing all potential optimal solutions. Figures 5
and 6 present the four objective functions of the
Pareto domain using two-dimensional projections.
Each of the 242 points on the graphs represents a
different fermentation simulated with a different set
of decision variables (start time for vacuum,
evaporation rate and condenser temperature).
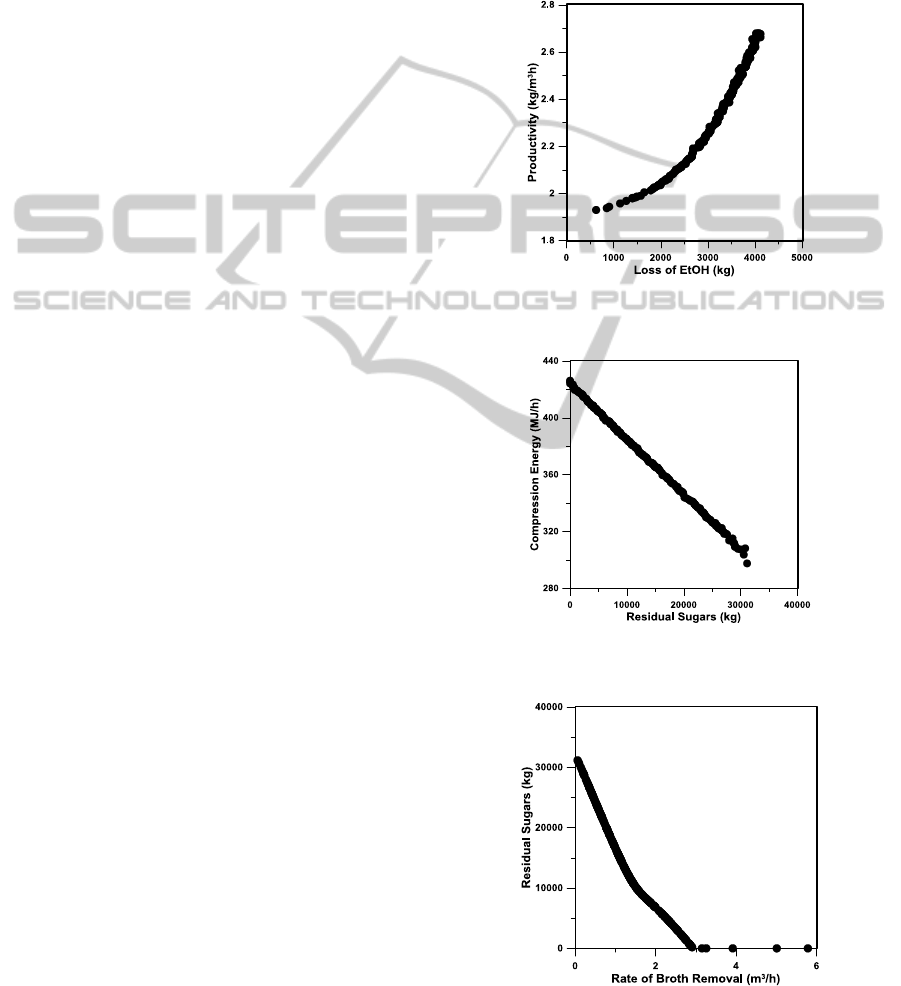
Figure 5 illustrates very well the compromises
that the Pareto domain expresses where an increase
in the productivity is accompanied by a greater loss
of ethanol. Similar compromise is expressed in
Figure 6 where the minimization of residual sugars
leads to an increase in the power of compression.
Two main reasons explain this compromise: (1) the
utilization of a greater quantity of xylose and
glucose leads to a higher production of carbon
dioxide, and (2) a greater sugar consumption rate
requires a higher removal rate of ethanol from the
broth in order to reduce product inhibition as shown
in Figure 7. Figure 7 shows very clearly that to
completely use glucose and xylose by reducing
product inhibition, the minimum fermentation
removal rate in the flash tank must be nearly 3 m
3
/h
when the flash tank vacuum system is put into
operation. Similarly (plots not shown), increasing
productivity is accompanied by a decrease in
residual sugars and increase in compression energy.
In this investigation, for simplicity and to reduce
the number of pieces of equipment, the carbon
dioxide stream was combined to the evaporated
broth stream. Using a traditional absorption column
to capture ethanol would reduce the power of
compression at the expense an additional column.
Information about the decision variables are
presented in Figures 8 and 9. The histogram of
Figure 8 reveals that for the majority of the solutions
within the Pareto domain, the vacuum flash tank was
put into operation in the vicinity of 20 h, in fact 21.1
± 5.8 h. This is where the level of ethanol
concentration starts to have a greater inhibiting
effect and some of it needs to be removed. It is
also more efficient to remove ethanol when the
concentration is higher. It would be possible to
refine the optimization by adding a stopping time for
the vacuum system as another decision or,
alternatively, adding the total fermentation time as a
decision variable. Either addition would have for
benefit to reduce the energy required for
compression.
Figure 5: Plot of ethanol productivity versus total ethanol
loss during fermentation.
Figure 6: Plot of the energy required for compression
versus the residual sugars at the end of fermentation.
Figure 7: Plot of residual sugars versus rate of broth
removal via vacuum boiling.
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
84
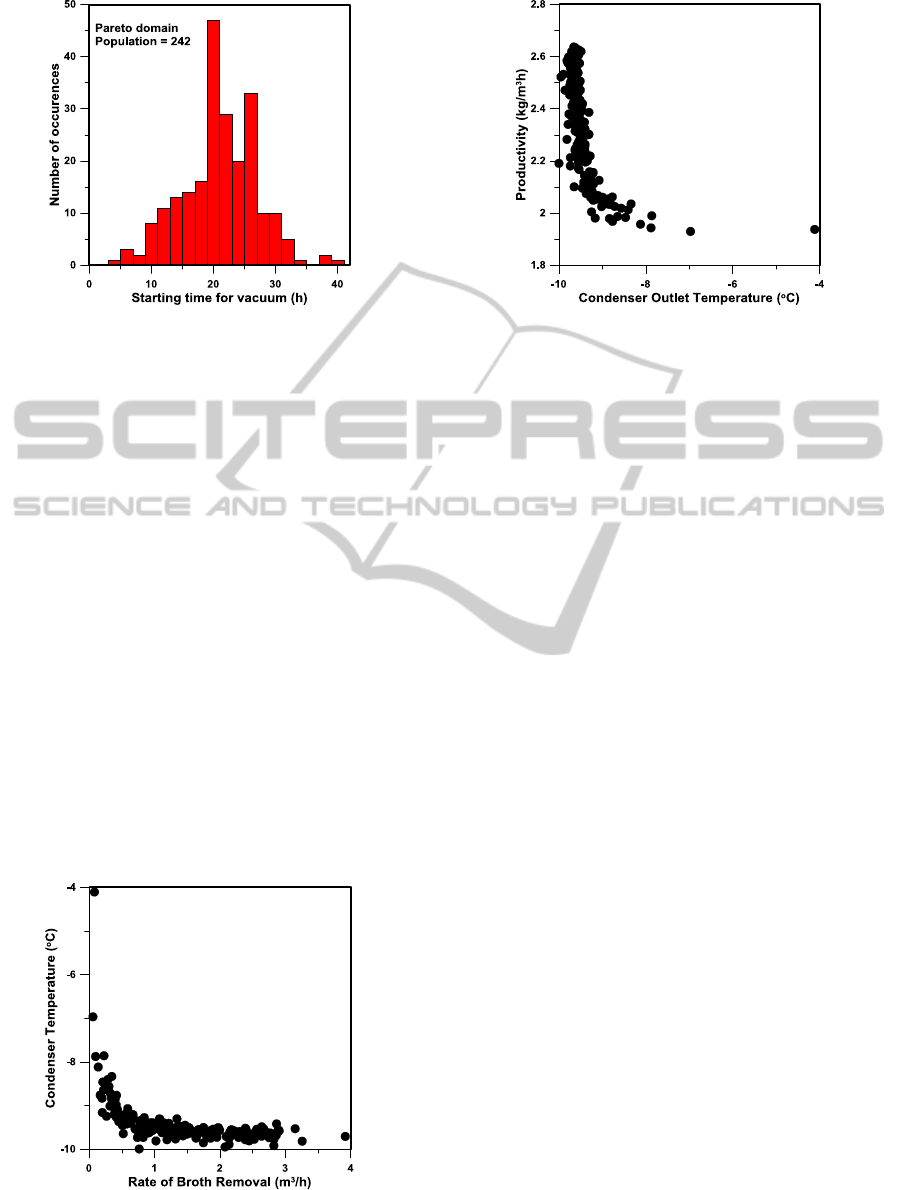
Figure 8: Histogram of the time at which the vacuum flash
tank is put into operation for Pareto-optimal solutions.
Figure 9 shows that as the rate of broth removal
via the vacuum flash tank is increased, the
temperature of the condenser needs to be lowered.
For most of the Pareto domain, the condenser
temperature hovers in the vicinity of its lower limit
of -10
o
C. Of course, a lower condensing temperature
will lead to lower ethanol loss but at greater
refrigerant expenses. A lower condensing
temperature leads to a higher productivity as shown
in Figure 10.
The current fermentation model was developed
for a fermenter operating at 30
o
C such that low
vacuum pressure due to thermodynamic limitation
had to be used to perform in situ ethanol recovery. If
the fermentation could occur at a higher
temperature, higher pressure could be used thereby
significantly reducing the cost. Microorganisms able
to tolerate higher fermentation temperature are
currently available but the productivity is yet too
low to compete with existing technology (Kumar et
al., 2010).
Figure 9: Plot the condenser outlet temperature versus the
rate of broth removal.
Figure 10: Plot of productivity versus condenser outlet
temperature.
5 CONCLUSIONS
The main goal of this paper was to examine, via the
simulation and optimization of a simple illustrative
example, the ease of combining Excel, VBA and
UniSim Design for optimizing industrial plants. This
investigation has shown that even for a simple
system, the time to access UniSim Design to pass
and retrieve information is relatively long. To
optimize a more complex plant, the time of
simulation will be a limiting factor with the
additional risk of not converging to a solution within
UniSim Design. It will be necessary to resort to
innovative and efficient methods to be able to
perform the optimization of a complex plant such as
the integrated first and second generation ethanol
production plant.
In this investigation, the bulk of the simulation
and optimization of the vacuum fermentation system
was performed within VBA with UniSim Design
performing thermodynamic and downstream
processing calculations. The Pareto domain was
circumscribed and allowed to observe very clearly
the compromises that need to be made when four
objective functions, mostly conflicting, were
optimized simultaneously.
ACKNOWLEDGEMENTS
The financial contribution of the Canadian National
Science and Engineering Research Council
(NSERC) is acknowledged.
Simulation and Multi-Objective Optimization of Vaccuum Ethanol Fermentation
85

REFERENCES
Cardona, C. A., Sanchez, O. J. 2007. Fuel ethanol
production: Process design trends and integration
opportunities. Bioresource Technology, 98,
2415-2457.
Deb, K. 2001. Multi-objective optimization using
evolutionary algorithms. New York: Wiley.
Dias, M. O. S., Maciel Filho, R., Maciel, M. R. W.,
Rossell, C.E.V., Bioethanol production from
sugarcane and sugarcane bagasse investigation of plant
performance and energy consumption. 18
th
International Congress of Chemical and Process
Engineering - CHISA, 2008.
Dias, M. O. S., Junqueira, T. L., Cavalett, O., Cunha, M.
P., Jesus, C. D. F., Rossell, C. E. V., Maciel Filho, R.,
Bonomi, A. 2012. Integrated versus stand-alone
second generation ethanol production from sugarcane
bagasse and trash. Bioresource Technology, 103, 152-
161.
Einicke, W.D., Gläser, B., Schöoullner, R. 1991. In-Situ
recovery of ethanol from fermentation broth by
hydrophobic adsorbents. Acta Biotechnologica, 11(4),
353-358.
Groot, W. J., Kraayenbrink, M. R., Waldram, R. H., Lans
R. G. J. M., Luyben K. Ch. A. M. 1992. Ethanol
production in an integrated process of fermentation
and ethanol recovery by pervaporation. 8, 99-111.
Haupt, R. L. and Haupt, S. E. 2004. Practical Genetic
Algorithms, 2
nd
Ed., John Wiley & Sons.
Kumar, S, Singh, S.P., Mishra, I.M., Adhikari, D.K. 2010.
Feasibility of ethanol production with enhanced sugar
concentration in bagasse hydrolysate at high
temperature using Kluyveromyces sp. IIPE453.
Biofuels, 1(5), 697-704.
Jassal, D.S., Zhang, Z., Hill, G.A. 2009. In-situ extraction
and purification of ethanol using commercial oleic
acid. Can. J. Chem. Eng., 72(5), 822-827.
Krissek, G. 2008. Future Opportunities and Challenges for
Ethanol Production and Technology. http://www.
farmfoundation.org/news/articlefiles/378-Krissek%
202-5-08.pdf.
Leksawasdi, N., Joachimsthal, E.L., Rogers, P.L. 2001.
Mathematical modelling of ethanol production from
glucose/xylose mixtures by recombinant Zymomonas
mobilis. Biotechnology Letters 23: 1087–1093.
Liu, H.S., Hsien-Wen, H. 1990. Analysis of gas stripping
during ethanol fermentation - I. In a continuous stirred
tank reactor. Chemical Engineering Science. 45(5),
1289-1299.
Mussatto, S.I., Dragone, G., Guimarães P.M.R., Silva,
J.P.A., Carneiro, L.M., Roberto, I.C., Vicente, A.,
Domingues, L., Teixeira, J.A. 2010. Technological
trends, global market, and challenges of bio-ethanol
production
Nguyen, V.D., Kosuge, H., Auresenia, J., Tan, R.,
Brondial, Y. 2009. Effect of vacuum pressure on
ethanol fermentation. Journal of Applied Sciences,
9(17), 3020-3026.
NRCan (March 24, 2009). Energy Sources. Consulted
August 5, 2011. Natural Resources Canada:
http://www.nrcan.gc.ca/eneene/sources/pripri/aboapr-
eng.php.
NRCan (January 4, 2011). Personal: Transportation.
Consulted August 8, 2011.Natural Resources Canada:
http://oee.nrcan.gc.ca/publications/infosource/pub/vehi
clefuels/ethanol/M92_257_2003.cfm.
Margeot, A., Hahn-Hagerdal, B., Edlund, M., Slade, R.,
Monot, F.. 2009. New improvements for
lignocellulosic ethanol, Curr. Opinions. Biotechnol.,
20, 372–380.
Park, C. H., Geng, Q. 1992. Simultaneous Fermentation
and Separation in the Ethanol and Abe Fermentation.
Separation and Purification Reviews, 21(2) 127-174.
Perrin, E., Mandrille, A., Oumoun, M., Fonteix, C., Marc,
I. (1997). Optimization globale par stratégie
d'évolution: Technique utilisant la Génétique des
individus diploides. RAIRO- Recherche Operationelle
31, 161-201.
Thibault, J. (2008). Net Flow and Rough Sets: Two
Methods For Ranking the Pareto Domain. In G.
Rangaiah (Ed.), Chapter 7 - Multi-Objective
Optimization: Techniques and Applications in
Chemical Engineering. World Scientific Publishing.
U.S. EIA (August 2010). Annual Energy Review
2009.ConsultedAugust 5, 2011, www.eia.gov/aer.
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
86
