
Channel-encoded and SVD-assisted MIMO Multimode Transmission
Schemes with Iterative Detection
Sebastian Aust, Andreas Ahrens and Steffen Lochmann
Hochschule Wismar, University of Technology, Business and Design, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany
Keywords:
Multiple-input Multiple-output (MIMO) System, Singular-value Decomposition (SVD), Bit Allocation,
Optical Fibre Transmission, Multimode Fiber (MMF), Bit-interleaved Coded Modulation (BICM).
Abstract:
In this contribution a coherent (2 × 2) MIMO (multiple input multiple output) transmission with iterative
detection over a measured multimode fiber channel at 1325 nm as well as at 1570 nm operating wavelength is
studied. For the channel measurements a fibre length of 1,4 km were chosen. Extrinsic information transfer
(EXIT) charts are used for analyzing and optimizing the convergence behaviour of the iterative demapping
and decoding. Our results show that in order to achieve the best bit-error rate, not necessarily all MIMO layers
have to be activated.
1 INTRODUCTION
Energy consumption of telecom networks has been
identified as an important research topic throughout
the recent past since energy costs contribute signifi-
cantly to network operator’s operational expenditures
(Baliga et al., 2009; Pickavet et al., 2008). Therefore
systems enabling energy-efficient data transmission
are mandatory for next generation network equip-
ment.
In the recent past the concept of MIMO (multiple
input multiple output) transmission over multimode
fibers has attracted increasing interest in the optical
fiber transmission community, e. g. (B¨ulow et al.,
2010; B¨ulow et al., 2011; Singer et al., 2008), target-
ing at increased fiber capacity. The concept of MIMO
transmission has been investigated since decades now
for both, twisted-pair copper cable transmission –
suffering from crosstalk between neighbouring wire
pairs – (Van Etten, 1975; Ahrens and Lange, 2006), as
well as for multi-antenna radio systems – where sig-
nal interference occurs on the radio interface (Telatar,
1999; Foschini, 1996).
A MIMO approach where modal dispersion is ex-
ploited, rather than avoided, is a promising solution.
Note that for a long time the multipath nature of wire-
less channels was viewed as a limiting factor to be
avoided. In recent years it has been realized that the
multipath nature of a channel can actually enhance
throughput and improve the quality of the data trans-
mission (i. e. minimize the bit-error rate) if it is prop-
erly exploited (Ahrens and Benavente-Peces, 2009b).
Bit-interleavedcoded modulation (BICM) was de-
signed for bandwidth efficient transmission over fad-
ing channels (Caire et al., 1998; Chindapol, 2001).
Wireless MIMO-BICM transmission schemes for
both non-frequency and frequency selective MIMO
channels have attracted a lot of attention and reached
a state of maturity (K¨uhn, 2006; Ahrens and
Benavente-Peces, 2009a). By contrast, MIMO-aided
optical systems require substantial further research
(Shah et al., 2005; Hsu et al., 2006; Lenz et al.,
2004). That is why in addition to bit loading al-
gorithms in this contribution the benefits of channel
coding are also investigated. The proposed iterative
decoder structures employ symbol-by-symbol soft-
output decoding based on the Bahl-Cocke-Jelinek-
Raviv (BCJR) algorithm and are analyzed under the
constraint of a fixed data throughput (Bahl et al.,
1974).
Against this background, the novel contribution
of this paper is that we jointly optimize the num-
ber of activated MIMO layers and the number of bits
per symbol combined with powerful error correct-
ing codes under the constraint of a given fixed data
throughput and integrity. The performance improve-
ments are exemplarily studied by computer simula-
tions at a measured 1,4 km multimode MIMO fiber
channel at 1325 nm and at 1570 nm operating wave-
length.
Since the ”design-space” is large, a two-stage op-
timization technique is considered. Firstly, the un-
353
Aust S., Ahrens A. and Lochmann S..
Channel-encoded and SVD-assisted MIMO Multimode Transmission Schemes with Iterative Detection.
DOI: 10.5220/0004018203530360
In Proceedings of the International Conference on Data Communication Networking, e-Business and Optical Communication Systems (OPTICS-2012),
pages 353-360
ISBN: 978-989-8565-23-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
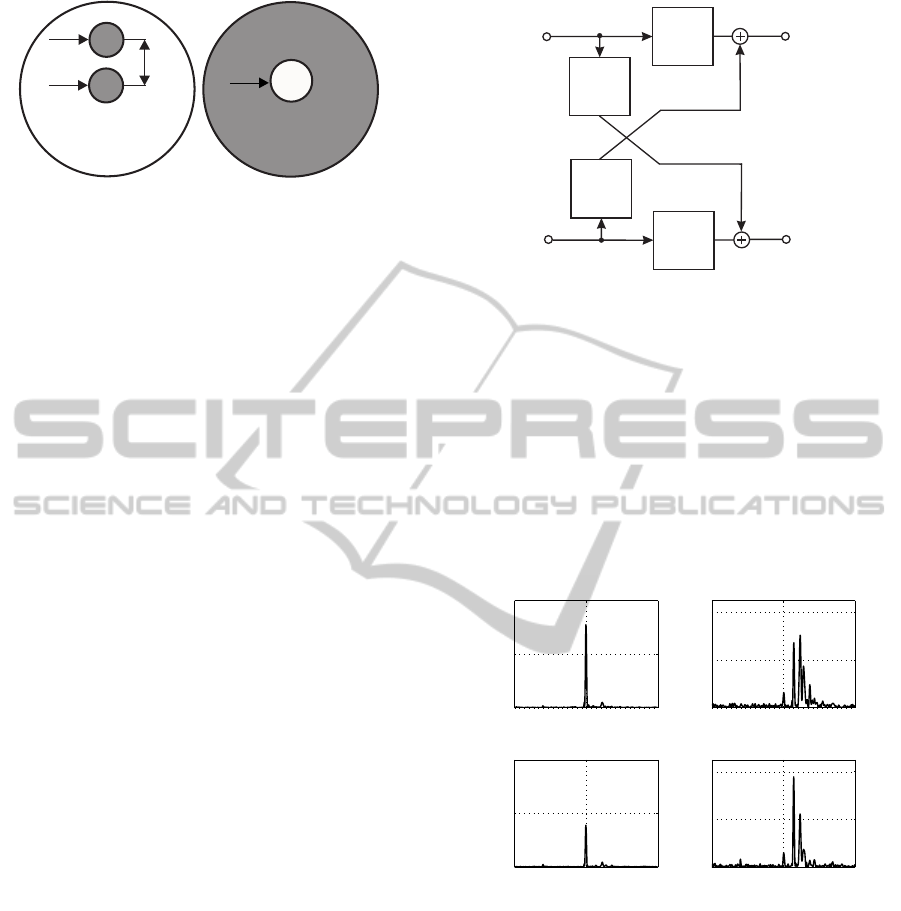
10µm
10µm
TX
2
TX
1
δ
RX
2
RX
2
RX
1
r
Figure 1: Forming the optical MIMO channel (left: light
launch positions at the transmitter side with a given eccen-
tricity δ, right: spatial configuration at the receiver side as a
function of the mask radius r).
coded MIMO scheme is analyzed, investigating the
allocation of both the number of bits per modulated
symbol and the number of activated MIMO layers at
a fixed data rate. Secondly, the optimized uncoded
system is extended by incorporating bit-interleaved
coded modulation using iterative detection (BICM-
ID), whereby both the uncoded as well as the coded
systems are required to supportthe same user data rate
within the same bandwidth.
The remaining part of this contribution is orga-
nized as follows: Section 2 introduces our system
model, while the proposed uncoded solutions are dis-
cussed in section 3. In section 4 the channel encoded
MIMO system is introduced. The associated perfor-
mance results are presented and interpreted in section
5. Finally, section 6 provides our concluding remarks.
2 CHANNEL MEASUREMENTS
AND MIMO SYSTEM MODEL
Forming the MIMO (multiple input multiple output)
system, the corresponding optical transmitter as well
as receiver side configuration is depicted in Fig. 1. At
the receiverside different spatial filters have been pro-
duced by depositing a metal layer at fiber end-faces
and subsequent ion milling (Pankow et al., 2011).
Details on the transmission model, which has been
determined by channel measurements, are given in
(Pankow et al., 2011).
2.1 MIMO Channel Measurements
For the investigated optical MIMO channel an eccen-
tricity δ of 10µm and a mask radius r of 15µm were
chosen (Fig. 1). The arising electrical (2× 2) MIMO
channel is highlighted in Fig. 2.
The obtained MIMO channel impulse responses
at 1325 nm and 1570 nm operating wavelength are
depicted in Fig. 3 and Fig. 4, respectively and show
the expected dependency from the operating wave-
u
s 1
(t)
u
s 2
(t)
u
k 1
(t)
u
k 2
(t)
g
11
(t)
g
21
(t)
g
12
(t)
g
22
(t)
Figure 2: Electrical (2× 2) MIMO system model.
length. The measured MIMO channel impulse re-
sponses at 1325 nm operating wavelength are high-
lighted in Fig. 3 and illustrate the activation of dif-
ferent mode groups according to the transmitter side
light launch conditions (Fig. 1). The individual mode
groups are clearly separated since almost no chro-
matic dispersion is imminent at the wavelength of
1325 nm. At a higher operating wavelength, i. e. 1570
nm, the separation of the different mode groups disap-
pears based on the additional effect of the chromatic
dispersion (Fig. 4).
0 2 4
0
1
2
0 2 4
0
0.2
0.4
0 2 4
0
1
2
0 2 4
0
0.2
0.4
t (inns) →t (inns) →
t (inns) →t (inns) →
T
s
g
1 1
(t) →
T
s
g
1 2
(t) →
T
s
g
2 1
(t) →
T
s
g
2 2
(t) →
Figure 3: Measured electrical MIMO impulse responses
with respect to the pulse frequency f
T
= 1/T
s
= 5,12 GHz
at 1325 nm operating wavelength.
2.2 MIMO Channel Parameters
In MMF two different sources of dispersion take
place, i. e. modal and chromatic dispersion. The
modal dispersion can be approximated by a weighted
Dirac delta impulse response
g
(νµ)
m
(t) =
N−1
∑
κ=0
g
(νµ)
mκ
δ(t − τ
0
− τ
κ
) . (1)
Therein, N is the number of propagating modes (i.e.
mode groups), g
(νµ)
mκ
describes the attenuation of the
OPTICS2012-InternationalConferenceonOpticalCommunicationSystems
354
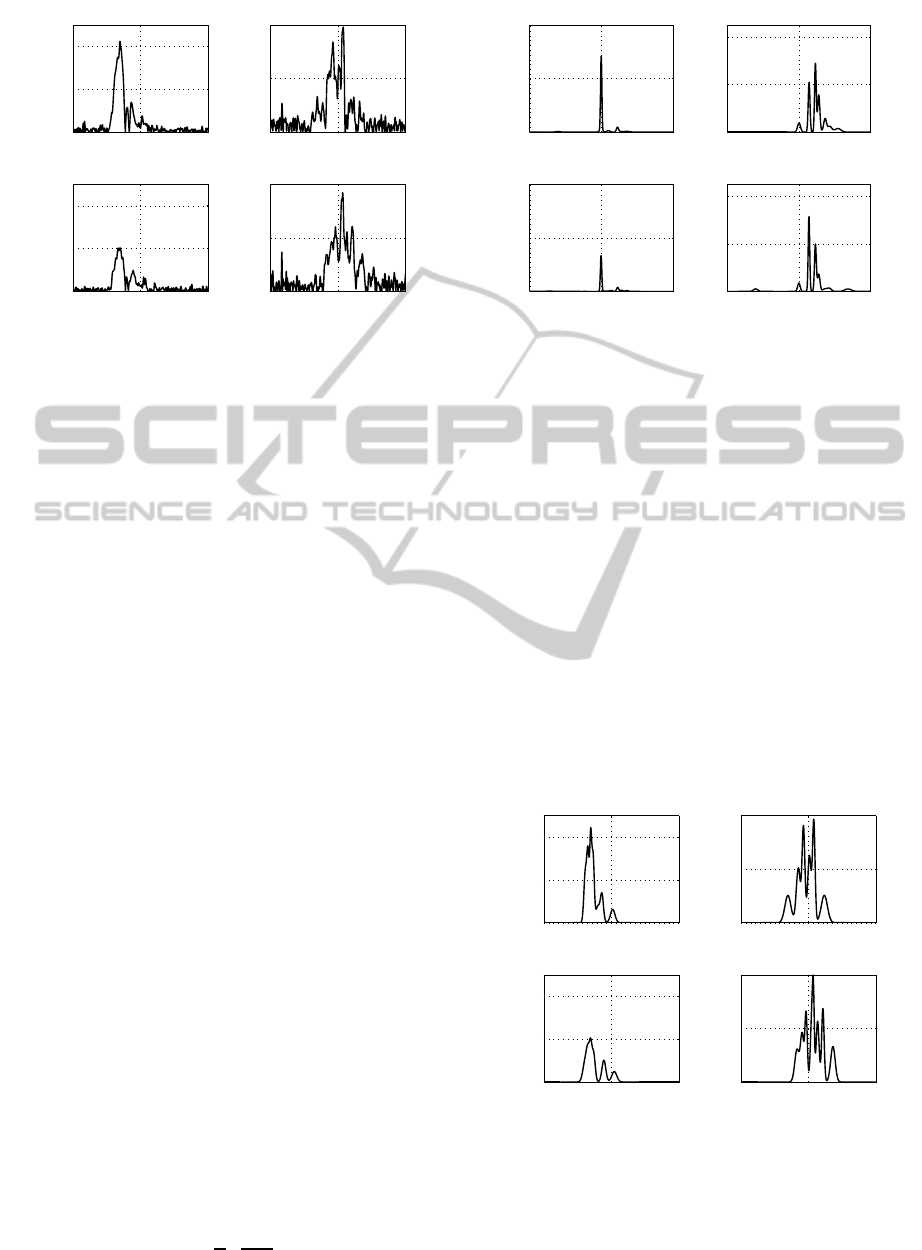
0 2 4
0
0.1
0.2
0 2 4
0
0.05
0.1
0 2 4
0
0.1
0.2
0 2 4
0
0.05
0.1
t (inns) →t (inns) →
t (inns) →t (inns) →
T
s
g
1 1
(t) →
T
s
g
1 2
(t) →
T
s
g
2 1
(t) →
T
s
g
2 2
(t) →
Figure 4: Measured electrical MIMO impulse responses
with respect to the pulse frequency f
T
= 1/T
s
= 5,12 GHz
at 1570 nm operating wavelength.
κth propagation mode (i. e. mode group) between
the µth input and the νth output, τ
κ
is the differential
modal delay with respect to the overall baseline delay
of τ
0
. In the presence of modal coupling, the attenua-
tion factor g
(νµ)
mκ
would become time-varying. Taking
the different SISO (single input single output) chan-
nels into consideration, the value g
(νµ)
mκ
expresses the
different contributions of the individual mode groups
to the SISO channels within the MIMO system. Since
almost no chromatic dispersion is imminent at the
wavelength of 1325 nm, the individual mode groups
are clearly separated as highlighted in Fig. 3.
As a result of the modal dispersion at the receiver
side, a single transmitted pulse may spread into a
number of adjacent symbol periods, depending on
the data rate, distance traveled, and fiber properties
(Singer et al., 2008). Practically, the weighted Dirac
delta pulses can be approximated by Gaussian pulses.
Fig. 5 shows the obtained impulse responses by using
Matlabs
R
curve fitting tool.
Another limit for MMF is given by the chromatic
dispersion, based on the frequency-dependenceof the
phase velocity of a wave. The transfer function of the
chromatic dispersion is given by
G
c
( f) = e
(π f τ
c
)
2
. (2)
Therein, the spectral width affecting parameter τ
c
re-
sults in
τ
c
= D
c
· δ
λ
· ℓ , (3)
with the parameter ℓ describing the fibre length. The
parameter δ
λ
represents the spectral width of the
source and D
c
is the group delay dispersion param-
eter, which depend on the refractive index n and the
operating wavelength λ, and is described as
D
c
= −
λ
c
·
d
2
n
dλ
2
. (4)
0 2 4
0
1
2
0 2 4
0
0.2
0.4
0 2 4
0
1
2
0 2 4
0
0.2
0.4
t (inns) →t (inns) →
t (inns) →t (inns) →
T
s
g
1 1
(t) →
T
s
g
1 2
(t) →
T
s
g
2 1
(t) →
T
s
g
2 2
(t) →
Figure 5: Approximated electrical MIMO impulse re-
sponses with respect to the pulse frequency f
T
= 1/T
s
=
5,12 GHz at 1325 nm operating wavelength by using
Matlabs
R
curve fitting tool.
In this work a fibre length of ℓ = 1,4 km is chosen.
The spectral width of the source is δ
λ
= 11 nm and
the group delay dispersion parameter is assumed to
be D
c
= 18 ps/(nm·km). The impulse response of
the chromatic dispersion g
c
(t) can be obtained by the
inverse Fourier transform of (2).
Finally, the multi-mode channel impulse response
between the µth input and the νth output can be ob-
tained as
g
νµ
(t) = g
(νµ)
m
(t) ∗ g
c
(t) . (5)
Fig. 6 shows the obtained SISO impulse responses
with modal and chromatic dispersion within the
MIMO system by using Matlabs
R
curve fitting tool.
0 2 4
0
0.1
0.2
0 2 4
0
0.05
0.1
0 2 4
0
0.1
0.2
0 2 4
0
0.05
0.1
t (inns) →t (inns) →
t (inns) →t (inns) →
T
s
g
1 1
(t) →
T
s
g
1 2
(t) →
T
s
g
2 1
(t) →
T
s
g
2 2
(t) →
Figure 6: Approximated electrical MIMO impulse re-
sponses with respect to the pulse frequency f
T
= 1/T
s
=
5,12 GHz at 1570 nm operating wavelength by using
Matlabs
R
curve fitting tool.
Channel-encodedandSVD-assistedMIMOMultimodeTransmissionSchemeswithIterativeDetection
355
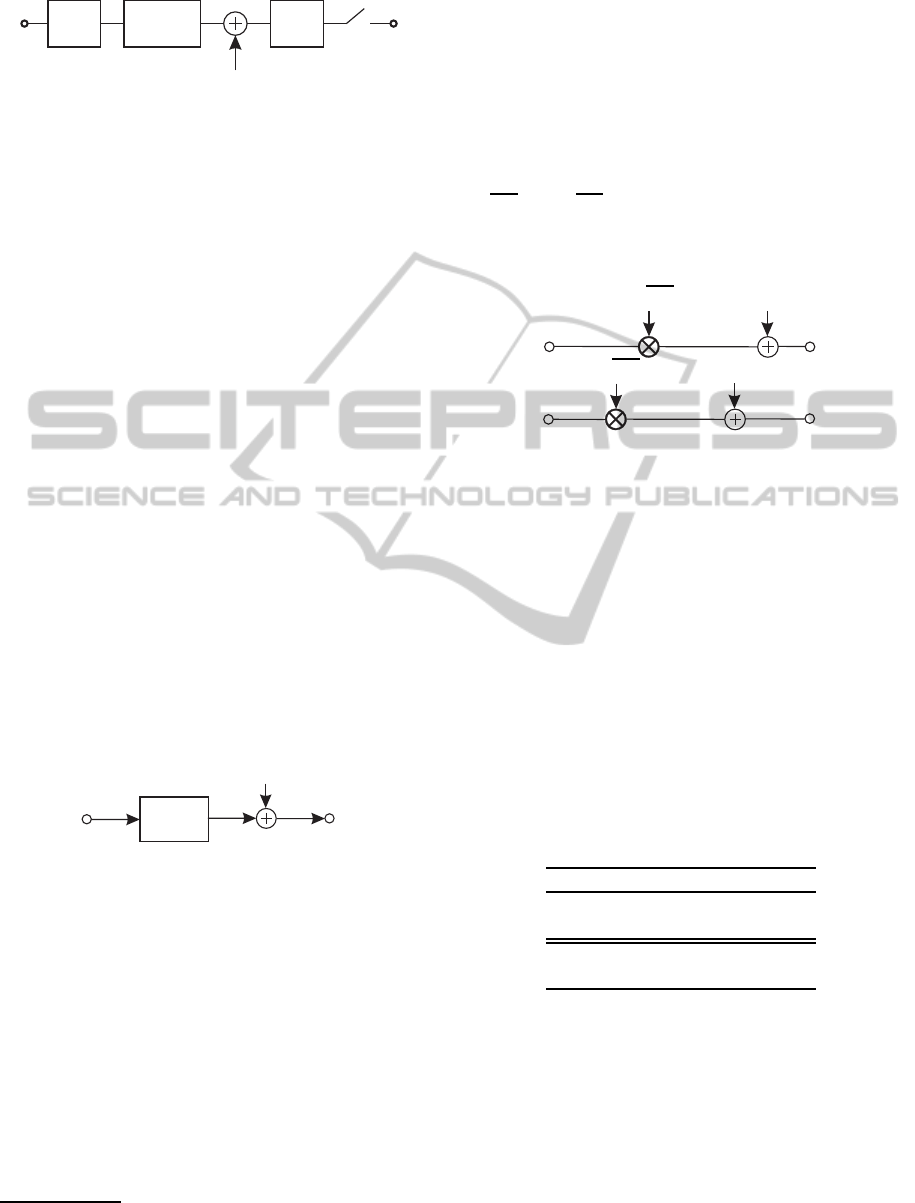
replacements
u
q µ
(t)
g
s
(t)
g
νµ
(t)
Ψ
0
g
ef
(t)
u
e ν
(k)
Figure 7: Mathematical representation of the MIMO related
single input single output (SISO) channels.
2.3 MIMO System Model
Fig. 7 illustrates the MIMO related single input sin-
gle output (SISO) channels. Rectangular pulses are
used for transmit and receive filtering. The baseband
finite-length impulse response of the MIMO channel
between the µth input and the νth output is given by
h
νµ
(t) = g
s
(t) ∗ g
νµ
(t) ∗ g
ef
(t) . (6)
The impulse responses of the transmit and receive fil-
tering are described by g
s
(t) and g
ef
(t).
The block diagram of the transmission model is
shown in Fig. 8: Coherent transmission and detec-
tion is assumed together with the modulation format
QAM (quadrature amplitude modulation) per MIMO
transmission mode. The block-oriented system for
frequency selective channels is modelled by:
u = H· c+ w . (7)
In (7), the transmitted signal vector c is mapped by
the channel matrix H onto the received vector u.
Finally, the vector of the additive, white Gaussian
noise (AWGN) is defined by w (Pankow et al., 2011;
Raleigh and Cioffi, 1998). Details on the transmission
model are given in (Pankow et al., 2011).
transmit vector
receive vector
noise vector
c
u
H
w
Figure 8: Transmission system model.
In MIMO communication, singular-value decom-
position (SVD) has been established as an efficient
concept to compensate the interferences between the
different data streams transmitted over a dispersive
channel: SVD is able to transfer the whole sys-
tem into independent, non-interfering layers exhibit-
ing unequal gains per layer as highlighted in Fig. 9.
The singular-value decomposition (SVD)
(Haykin, 2002) of the system matrix H results in:
H = S · V · D
H
, where S and D
H
are unitary matrices
and V is a real-valued diagonal matrix of the positive
square roots of the eigenvalues of the matrix H
H
H
sorted in descending order
1
.
1
The transpose and conjugate transpose (Hermitian) of
D are denoted by D
T
and D
H
, respectively.
The MIMO data vector c is now multiplied by the
matrix D before transmission. In turn, the receiver
multiplies the received vector u by the matrix S
H
. In
doing so, neither the transmit power budget nor the
noise power characteristic is changed. The overall
transmission relationship is defined as
y = S
H
(H· D· c+ w) = V· c+ ˜w. (8)
The unequal gains per layer, i. e., the diagonalelement
p
ξ
1k
and
p
ξ
2k
of the matrix V at the time instant k,
are defined by the positive square roots of the eigen-
values of the matrix H
H
H (Fig. 9).
p
ξ
1 k
p
ξ
2 k
˜w
1 k
˜w
2 k
c
1 k
c
2 k
y
1 k
y
2 k
Figure 9: SVD-based layer-specific transmission model.
3 OPTIMIZATION APPROACH
By taking the different layer-specific weighting, in-
troduced by the positive square roots of the eigenval-
ues of the matrix H
H
H, into account (Fig. 9), bit- and
power loading per layer can be used to balance the bit-
error probabilities and thus optimize the performance
of the whole transmission system. Given a fixed trans-
mission bit rate, the optimization target is a minimum
BER: Therefore the bit loading to the different trans-
mission modes is optimized according to the options
shown in Table 1.
Table 1: Parameters for bitloading: investigated QAM
transmission modes for fixed transmission bit rate.
throughput layer 1 layer 2
4 bit/s/Hz 16 0
4 bit/s/Hz 4 4
2 bit/s/Hz 4 0
2 bit/s/Hz 2 2
4 CHANNEL-ENCODED MIMO
SYSTEM
BICM is constituted by the concatenation of an en-
coder, an interleaver and a mapper, which is extended
here to a BICM-MIMO scheme, where different sig-
nal constellations are mapped appropriately to differ-
ent layers.
OPTICS2012-InternationalConferenceonOpticalCommunicationSystems
356
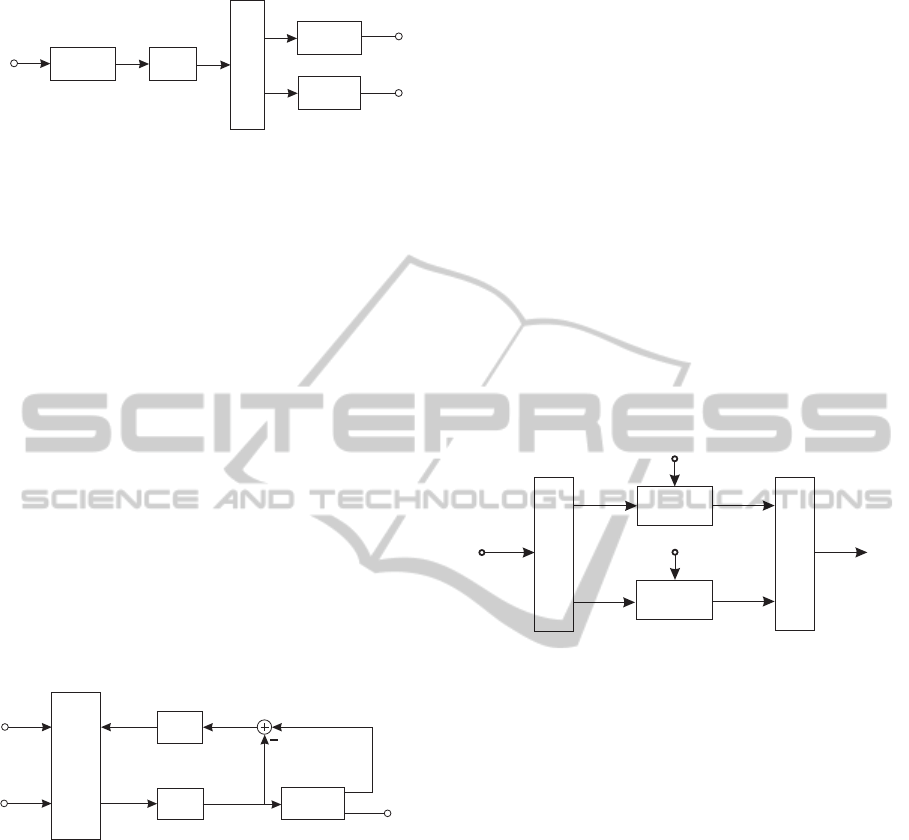
i
b
˜
b
c
1 k
c
2 k
encoder
∏
Mapper
Mapper
˜
b
1
˜
b
2
MUX and Buffer
Figure 10: The channel-encoded MIMO transmitter struc-
ture.
The channel-encoded transmitter structure is de-
picted in Fig. 10. The encoder employs a
half-rate non-systematic, non-recursive convolutional
(NSNRC) code using the generator polynomials (7,5)
in octal notation. The uncoded information is orga-
nized in blocks of N
i
bits, consisting of at least 3000
bits, depending on the specific QAM constellation
used. Each data block i is encoded and results in the
block b consisting of N
b
= 2N
i
+ 4 encoded bits, in-
cluding 2 termination bits. The encoded bits are in-
terleaved using a random interleaver and stored in the
vector
˜
b. The encoded and interleaved bits are then
mapped to the MIMO layers. The task of the multi-
plexer and buffer block of Fig. 10 is to divide the vec-
tor of encoded and interleaved information bits, i.e.
˜
b, into subvectors according to the chosen transmis-
sion mode (Table 1). The individual binary data vec-
tors are then mapped to the QAM symbols c
1k
and
c
2k
according to the specific mapper used (Fig. 9 and
Fig. 10).
y
1 k
y
2 k
Soft Demapper
L
(ν)
2
(
˜
b)
∏
−1
∏
L
(ν)
a,1
(b)
decoder
L
(ν)
1
(i)
L
(ν)
1
(b)
L
(ν−1)
e,1
(b)
L
(ν)
a,2
(
˜
b)
Figure 11: Iterative demodulator structure.
The iterative demodulator structure is shown in
Fig. 11 (Ahrens et al., 2008).
When using the iteration index ν, the first iteration
of ν = 1 commences with the soft-demapper deliver-
ing the N
b
log-likelihood ratios (LLRs) L
(ν=1)
2
(
˜
b) of
the encoded and interleaved information bits, whose
de-interleaved version L
(ν=1)
a,1
(b) represents the input
of the convolutional decoder as depicted in Fig. 11
(Bahl et al., 1974; K¨uhn, 2006). This channel de-
coder provides the estimates L
(ν=1)
1
(i) of the original
uncoded information bits as well as the LLRs of the
N
b
NSNRC-encoded bits in the form of
L
(ν=1)
1
(b) = L
(ν=1)
a,1
(b) + L
(ν=1)
e,1
(b) . (9)
As seen in Fig. 11 and (9), the LLRs of the NSNRC-
encoded bits consist of the receiver’s input signal it-
self plus the extrinsic information L
(ν=1)
e,1
(b), which
is generated by subtracting L
(ν=1)
a,1
(b) from L
(ν=1)
1
(b).
The appropriately ordered, i.e. interleaved extrinsic
LLRs are fed back as a priori information L
(ν=2)
a,2
(
˜
b)
to the soft demapper of Fig. 11 for the second itera-
tion.
Following the detailed structure of the soft-
demapper in Fig. 12, the N
b
LLRs L
(ν)
2
(
˜
b) are com-
posed of sub-blocks (L
(ν)
2
(
˜
b
1
),L
(ν)
2
(
˜
b
2
)). Each vec-
tor L
(ν)
2
(
˜
b
ℓ
) (with ℓ = 1,2) is generated by the soft
demapper from the MIMO channels’ output y
ℓ,k
and
the a priori information L
(ν)
a,2
(
˜
b
ℓ
) (with ℓ = 1,2) pro-
vided by the channel decoder. After the first iteration,
this a priori information emerges from the N
b
LLRs
L
(ν)
a,2
(
˜
b).
MUXandBuffer
DEMUXandBuffer
y
1
(k)
y
2
(k)
Soft-
Soft-
Demapper
Demapper
L
(ν)
2
(
˜
b
1
)
L
(ν)
2
(
˜
b
2
)
L
(ν)
a,2
(
˜
b
1
)
L
(ν)
a,2
(
˜
b
2
)
L
(ν)
2
(
˜
b)
L
(ν)
a,2
(
˜
b)
Figure 12: Detailed soft demapper demodulator structure.
5 RESULTS
The numerical analysis targets at BER results. For
this purpose it is assumed, that each optical input
within the multimode fiber is fed by a system with
identical mean properties with respect to transmit fil-
ter and pulse frequency f
T
= 1/T
s
. For numerical as-
sessment within this paper,the pulse frequencyis cho-
sen to be f
T
= 5,12 GHz, the average transmit power
is supposed to be P
s
= 1V
2
– this equals 1 W at a lin-
ear and constant resistance of 1Ω – and as an external
disturbance a white Gaussian noise with power spec-
tral density N
0
is assumed (Pankow et al., 2011). In
order to transmit at a fixed data rate while maintain-
ing the best possible integrity, i. e., bit-error rate, an
appropriate number of MIMO layers has to be used,
which depends on the specific transmission mode, as
detailed in Tab. 1.
5.1 Uncoded MIMO System
The optimization results, obtained by computer simu-
lation at an overall data rate of 20,48 Gbps, are shown
Channel-encodedandSVD-assistedMIMOMultimodeTransmissionSchemeswithIterativeDetection
357
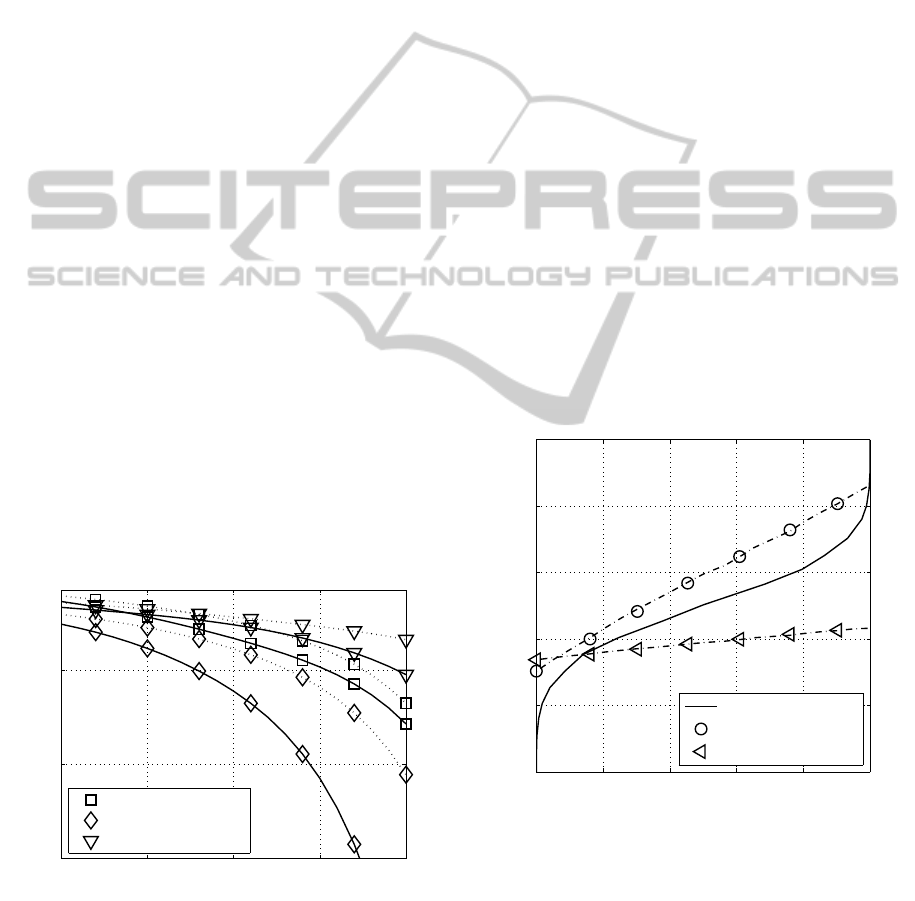
in Fig. 13 for different operating wavelength: The
BER becomes minimal in case of an optimized bit
loading (Fig. 13) with highest bit loading in the layer
with largest singular values. The optimized MIMO
transmission exhibits an improvement with respect to
SISO transmission, but a non-optimized MIMO trans-
mission leads to a significant degradation of the sys-
tem performance. Furthermore, the simulation results
show that in order to minimize the overall BER at a
fixed data rate, not necessarily all MIMO layer should
be activated. Instead, only the strongest MIMO layers
should be used with appropriate modulation levels in
the considered example.
Furthermore, as obtained by the channel measure-
ments (Fig. 3 and Fig. 4), at a higher operating wave-
length, i. e. 1570 nm, the separation of the differ-
ent mode groups disappears based on the effect of
the chromatic dispersion. Since the chromatic disper-
sion affects all mode groups almost equally, MIMO
isn’t able to generate an additional diversity gain
(in comparison to wireless channels, where delay-
spread isn’t any longer a limiting parameter (Ahrens
and Benavente-Peces, 2009b; Ahrens and Benavente-
Peces, 2011)). The advantage of a higher signal-to-
noise-ratio due to lower attenuation in the third op-
tical window is diminished by the chromatic disper-
sion. Therefore, the obtained bit-error rate results
are higher at 1570 nm compared to 1325 nm. How-
ever, dispersion compensation schemes are well es-
tablished in optical communications and they are not
considered as a practical limitation.
However, uncoded systems have reached a state
of maturity. By contrast coded MIMO configurations
require substantial further research.
20 25 30 35 40
10
−6
10
−4
10
−2
10 · log
10
(P
s
T
s
/N
0
) (indB) →
bit-error rate →
16-QAM, SISO
(16,0)-QAM, MIMO
(4,4)-QAM, MIMO
Figure 13: BER performance at 1570 nm operating wave-
length (dotted line) and at 1325 nm operating wavelength
(solid line) when using the transmission modes introduced
in Tab. 1 and transmitting 4 bit/s/Hz over frequency selec-
tive optical MIMO channels.
5.2 Channel Encoded MIMO System
The joint optimization of the number of activated
MIMO layers as well as the number of bits per sym-
bol was found to be effective at high SNRs. However,
iterative receivers are able to work in a much lower
SNR region. Therefore it would be interesting to see
how the design criteria change when coding is added
to the transmission system.
Using the half-rate, constraint-length K
cl
= 3
NSNRC code with the generator polynomialsof (7,5)
in octal notation, the BER performance is analyzed
for an effective throughput of 2 bit/s/Hz based on the
best uncoded schemes of Table 1. In addition to the
number of bits per symbol and the number of acti-
vated MIMO layers, the achievable performance of
the iterative decoder is substantially affected by the
specific mapping of the bits to both the QAM sym-
bols as well as to the MIMO layers. Here, the max-
imum iteration gain can only be guaranteed, if anti-
Gray mapping is used on all activated MIMO layers
(Chindapol, 2001).
Furthermore, observed by comparing the extrinsic
information transfer (EXIT) chart results of Fig. 14
and 15, the overall performance is strongly influenced
by the allocation of the number of bits to the MIMO
layers.
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
extrinsic demapper output →
extrinsic decoder output →
NSNRC code
(16,0) QAM, MIMO
(4,4) QAM, MIMO
Figure 14: EXIT chart for an effective user-data through-
put of 2 bit/s/Hz and the different QAM constellations at
10log
10
(P
s
T
s
/N
0
) = 18 dB (1325 nm operating wavelength
and anti-Gray mapping on all activated MIMO layers).
In order to guarantee an open EXIT tunnel and
therefore an efficient information exchange between
the soft demapper transfer characteristic and the de-
coder transfer characteristic at a given signal-to-noise
OPTICS2012-InternationalConferenceonOpticalCommunicationSystems
358
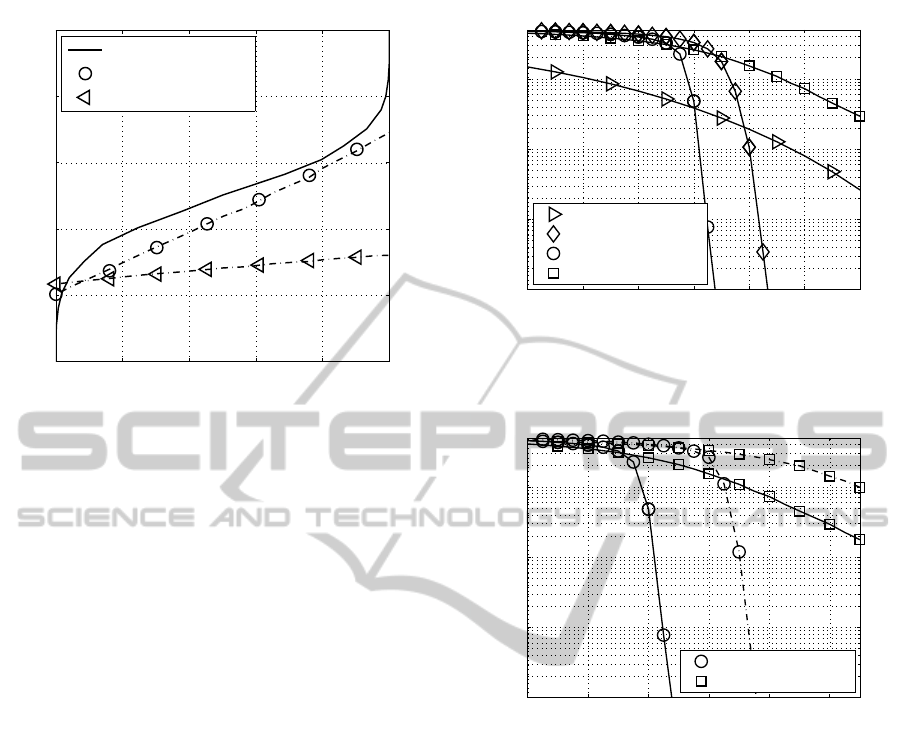
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
extrinsic demapper output →
extrinsic decoder output →
NSNRC code
(16,0) QAM, MIMO
(4,4) QAM, MIMO
Figure 15: EXIT chart for an effective user-data through-
put of 2 bit/s/Hz and the different QAM constellations at
10log
10
(P
s
T
s
/N
0
) = 18 dB (1570 nm operating wavelength
and anti-Gray mapping on all activated MIMO layers).
ratio, not necessarily all MIMO should be activated.
In the considered example only the strongest MIMO
layer should be used with appropriate modulation
level. Activating all MIMO layers the information
exchange between the soft demapper and the decoder
stops relatively early, resulting in a reduced BER per-
formance.
Furthermore, it turns out that chromatic dispersion
combined with the specific QAM constellation sizes,
as detailed in Tab. 1, leads to a degradation of the
overall performance as expected.
The BER performance is presented in Fig. 16
based on the different schemes of Table 1 and con-
firms the EXIT chart results. The information word
length is 3000 bits and a random interleaver is ap-
plied.
Fig. 17 illustrates the wavelength-dependent BER
performance. As already stated by the EXIT charts re-
sults, the chromatic dispersion leads to a degradation
of the overall performance.
The inferior performance is also indicated by the
corresponding BER curves shown in Fig. 17.
6 CONCLUSIONS
Coherent MIMO transmission over measured multi-
mode optical fibers has been investigated targeting at
minimized BER while keeping the transmission bit-
rate constant. The results show that MIMO trans-
mission based on SVD is a promising approach, in
particular when the bit loading is optimized. In that
12 14 16 18 20 22 24
10
−4
10
−3
10
−2
10
−1
10 · log
10
(E
s
/N
0
) (in dB) →
bit-error rate →
(4,0) QAM, uncoded
(16,0) QAM, 3 Iter.
(16,0) QAM, 10 Iter.
(4,4) QAM, 10 Iter.
Figure 16: BERs assuming anti-Gray mapping scheme
on the activated MIMO layers for an effective user-data
throughput of 2 bit/s/Hz (1325 nm operating wavelength).
14 16 18 20 22 24
10
−4
10
−3
10
−2
10
−1
10 · log
10
(E
s
/N
0
) (in dB) →
bit-error rate →
(16,0) QAM, 10 Iter.
(4,4) QAM, 10 Iter.
Figure 17: BER comparison at 1325 nm operating wave-
length (solid line) and at 1570 nm operating wavelength
(dotted line) assuming anti-Gray mapping scheme on the
activated MIMO layers for an effective user-data through-
put of 2 bit/s/Hz.
case significant BER improvements can be achieved
compared to a conventional SISO system. The pro-
posed MIMO-BICM scheme includes an adaptation
of the transmit parameters. EXIT charts are used for
analysing and optimizing the convergence behaviour
of iterative demapping and decoding. Here, the choice
of the number of bits per symbol and the number of
MIMO layers combined with powerful error correct-
ing codes substantially affects the performance of a
MIMO system, suggesting that not all MIMO layers
have to be activated in order to achieve the best BERs.
ACKNOWLEDGEMENTS
The authors wish to thank their co-worker, Mr. Stef-
fen Schr¨oder, for supporting the measurement cam-
Channel-encodedandSVD-assistedMIMOMultimodeTransmissionSchemeswithIterativeDetection
359

paign.
REFERENCES
Ahrens, A. and Benavente-Peces, C. (2009a). Modulation-
Mode and Power Assignment for Broadband MIMO-
BICM Schemes. In IEEE 20th Personal, Indoor and
Mobile Radio Communications Symposium (PIMRC),
Tokio (Japan).
Ahrens, A. and Benavente-Peces, C. (2009b). Modulation-
Mode and Power Assignment in Broadband MIMO
Systems. Facta Universitatis (Series Electronics and
Energetics), 22(3):313–327.
Ahrens, A. and Benavente-Peces, C. (2011). Modulation-
Mode Assignment in Iteratively Detected and SVD-
assisted Broadband MIMO Systems. In Filipe, J. and
Obaidat, M. S., editors, E-business and Telecommuni-
cations, Communications in Computer and Informa-
tion Science, pages 307–319. Springer, Berlin, Hei-
delberg.
Ahrens, A. and Lange, C. (2006). Exploitation of Far-
End Crosstalk in MIMO-OFDM Twisted Pair Trans-
mission Systems. In IASTED International Confer-
ence on Wireless Networks and Emerging Technolo-
gies (WNET), Banff, Alberta (Kanada).
Ahrens, A., Ng, S. X., K¨uhn, V., and Hanzo, L. (2008).
Modulation-Mode Assignment for SVD-Aided and
BICM-Assisted Spatial Division Multiplexing. Phys-
ical Communications (PHYCOM), 1(1):60–66.
Bahl, L. R., Cocke, J., Jelinek, F., and Raviv, J. (1974).
Optimal Decoding of Linear Codes for Minimizing
Symbol Error Rate. IEEE Transactions on Informa-
tion Theory, 20(3):284–287.
Baliga, J., Ayre, R., Hinton, K., Sorin, W. V., and
Tucker, R. S. (2009). Energy Consumption in Opti-
cal IP Networks. Journal of Lightwave Technology,
27(13):2391–2403.
B¨ulow, H., Al-Hashimi, H., and Schmauss, B. (2010). Sta-
ble Coherent MIMO Transport over Few Mode Fiber
Enabled by an Adiabatic Mode Splitter. In European
Conference and Exhibition on Optical Communica-
tion (ECOC), page P4.04, Torino, Italy.
B¨ulow, H., Al-Hashimi, H., and Schmauss, B. (2011).
Coherent Multimode-Fiber MIMO Transmission with
Spatial Constellation Modulation. In European Con-
ference and Exhibition on Optical Communication
(ECOC), Geneva, Switzerland.
Caire, G., Taricco, G., and Biglieri, E. (1998). Bit-
Interleaved Coded Modulation. IEEE Transactions on
Information Theory, 44(3):927–946.
Chindapol, A. Ritcey, J. A. (2001). Design, Analysis, and
Performance Evaluation for BICM-ID with square
QAM Constellations in Rayleigh Fading Channels.
IEEE Journal on Selected Areas in Communications,
19(5):944–957.
Foschini, G. J. (1996). Layered Space-Time Architecture
for Wireless Communication in a Fading Environment
when using Multiple Antennas. Bell Labs Technical
Journal, 1(2):41–59.
Haykin, S. S. (2002). Adaptive Filter Theory. Prentice Hall,
New Jersey.
Hsu, R. C. J., Tarighat, A., Shah, A., Sayed, A. H., and
Jalali, B. (2006). Capacity Enhancement in Coherent
Optical MIMO (COMIMO) Multimode Fiber Links.
IEEE Communications Letters, 10(3):195–197.
K¨uhn, V. (2006). Wireless Communications over MIMO
Channels – Applications to CDMA and Multiple An-
tenna Systems. Wiley, Chichester.
Lenz, D., Rankov, B., Erni, D., B¨achtold, W., and Wit-
tneben, A. (2004). MIMO Channel for Modal Mul-
tiplexing in Highly Overmoded Optical Waveguides.
In International Zurich Seminar on Communications
(IZS), Zurich,Switzerland.
Pankow, J., Aust, S., Lochmann, S., and Ahrens, A. (2011).
Modulation-Mode Assignment in SVD-assisted Op-
tical MIMO Multimode Fiber Links. In 15th Inter-
national Conference on Optical Network Design and
Modeling (ONDM), Bologna (Italy).
Pickavet, M., Vereecken, W., Demeyer, S., Audenaert, P.,
Vermeulen, B., Develder, C., Colle, D. Dhoedt, B.,
and Demeester, P. (2008). Worldwide Energy Needs
for ICT: the Rise of Power-Aware Networking. In
International Symposium on Advanced Networks and
Telecommunication Systems (ANTS), Bombay, India.
Raleigh, G. G. and Cioffi, J. M. (1998). Spatio-Temporal
Coding for Wireless Communication. IEEE Transac-
tions on Communications, 46(3):357–366.
Shah, A., Hsu, R. C. J., Tarighat, A., Sayed, A. H.,
and Jalali, B. (2005). Coherent Optical MIMO
(COMIMO). Journal Of Lightwave Technology,
23(8):2410–2419.
Singer, A. C., Shanbhag, N. R., and Bae, H.-M. (2008).
Electronic Dispersion Compensation – An Overwiew
of Optical Communications Systems. IEEE Signal
Processing Magazine, 25(6):110 – 130.
Telatar, E. (1999). Capacity of Multi-Antenna Gaussian
Channels. European Transactions on Telecommuni-
cations, 10(6):585–595.
Van Etten, W. (1975). An Optimum Linear Receiver
for Multiple Channel Digital Transmission Systems.
IEEE Transactions on Communications, 23(8):828–
834.
OPTICS2012-InternationalConferenceonOpticalCommunicationSystems
360
