
Self-ad-MCNHA-SLOS
A Self-adaptive Minimum-Cost Network Hardening Algorithm based on Stochastic
Loose Optimize Strategy
Yonglin Sun, Yongjun Wang and Yi Zhang
College of Computer Science, National University of Defense Technology (NUDT), Changsha, P.R. China
Keywords: Minimum-cost Network Hardening, Stochastic Loose Optimize, Self-adaptive, Network Vulnerability,
Attack Graph.
Abstract: Given a network, it inevitable contains various vulnerabilities, which could be exploited by malicious
attackers. It is an effective way to harden a network by searching and remedying those critical
vulnerabilities. That is the so-called Minimum-Cost Network Hardening (MCNH) problem, but there
haven’t any effective enough method to address this problem yet, especially, when facing large-scale
network. We proposed Self-ad-MCNHA-SLOS, an algorithm using Stochastic Loose Optimize Strategy
(SLOS) and self-adaptive parameter adjustment method ingeniously, to meet the problem. Experiment
results show that it has the merits of high-efficiency, controllable, asymptotically optimal, and suitable for
large-scale network.
1 INTRODUCTION
Networks changed and are changing people’s life,
anyone and anything could be tied together by the
Internet to share the benefits of interconnected and
information sharing. However, the neglect of
security in the history of network techniques
development is becoming a nightmare. Drived by
economic interests, hacker industry chains create
uncountable malwares and attack techniques
threatening to legitimate users continuously by
finding and exploiting vulnerabilities in networks,
network security is becoming more and more serious.
Network vulnerability means those exploitable
defects existing in network environment, which
could be exploited by adversaries to do harm to the
network and its users, such as software bugs,
protocol defects, security policy conflicts,
unreasonable network structure, etc. MCNH is based
on network vulnerability association analysis and
target for finding minimum-cost hardening plan for
those critical resources. (Jha, 2002) proposed the
most original concept of MCNH based on state
attack graph. Since then, several teams addressed
this problem and made significant improvements but
still unsolved.
The MCNH problem contains 3H questions: how
to determine the whole space of possible hardening
plans, how to determine the cost of a hardening plan,
and how to find the effective minimum-cost
hardening plan. Attack graph can be used to
determine the whole plan space and the validity
criteria of plan, since it can reflect the exploit-
dependence relations among all of the vulnerabilities
existing in given network. Usually, the costs of plans
are assumed to be known for the complexity and
subjectivity of plan cost evaluation. As to the third H,
we assume there are N nodes in a given network,
then, the scale of vulnerabilities is O(N), and the
scale of possible plans is 2
O(N)
, it is NP hard to find
the effective minimum-cost hardening plan. It will
become unfulfillable to solve this problem
accurately, when facing large-scale network
environment.
We proposed Self-ad-MCNHA-SLOS to find
minimum-cost plans (Min-Plan) iteratively from an
array of stochastic sparse sub-spaces (Sparse-Space)
of the whole possible hardening plan space (Plan-
Space), and updates the approximate optimal
hardening plan (Approx-Opt-Plan) according to the
validity of those Min-Plans judged by the validity
judgment function (Valid()). It also uses the history
validity information of those Min-Plans to adjust the
parameter (density) of the hardening plan generator
(GeneratePlan()) to make sure those Sparse-Spaces
converge quickly to the optimal hardening plan
372
Sun Y., Wang Y. and Zhang Y..
Self-ad-MCNHA-SLOS - A Self-adaptive Minimum-Cost Network Hardening Algorithm based on Stochastic Loose Optimize Strategy.
DOI: 10.5220/0004022803720378
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 372-378
ISBN: 978-989-8565-24-2
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

(Opt-Plan). In this way, it can make sure the
Approx-Opt-Plan obtained by iterations of limited
steps closes enough to the Opt-Plan. Testified both
by theoretical analysis and experiments evaluation,
Self-ad-MCNHA-SLOS has the merits of high-
efficiency, controllable and asymptotically optimal,
and is very suitable for large-scale network
environment.
2 RELATED WORK
MCNH is based on attack graph, (Swiler, 2001) first
proposed the attack graph model. (Sheyner, 2002)
studied the automation of attack graph generation
and analysis. (Ammann, 2002) first proposed
attacker’s ability monotonic assumption to improve
the efficiency of attack graph construction. (R. P.
Lippmann, 2005) proposed network security
assessment and hardening method based on attack
graph. (Ou, 2005) proposed a method with
computational complexity between O(N
2
) and O(N
3
)
to construct single-objective attack graph, and found
the phenomenon of circle-included attack paths.
(Ingols, 2006) implement a prototype system to
generate multiple-prerequisite attack graph for large-
scale enterprise network using raw data collected
from real network environment. (Chen, 2009)
proposed an algorithm to generate multi-objective
attack graph. Besides, researchers have also
proposed various methods to enhance the
intelligibility and usability of attack graph for its
complicated (Mehta, 2006); (Lippmann, 2007);
(Homer, 2008).
As for MCNH, (Jha, 2002) proposed the original
concept of MCNH based on state attack graph, their
work is to looking for the minimum safety measure
set to guarantee the safety of the key information
assets of a given network. Since then, (Noel, 2003)
proposed MCNH measure set based on attribute
attack graph, however, it can’t be applied to large
attack graph with circles. Though (Wang, 2006)
used one-pass search strategy to avoid logic loops in
attack graph, it still can’t be applied to large-scale
attack graph. (Homer, 2008) proposed an automatic
network configuration management method to help
for making network configuration decision in an
iterative approach, but it still not efficiency enough
when attack graph is moderate large. (Chen, 2008)
proposed an accurate method to calculate optimal
hardening plan based on Binary Decision Diagrams
(BDD) and an approximate one based on greedy
strategy, the former is better than Lingyu Wang’s
method, but still a method for small-scale network,
while the latter one is theoretically appropriate for
large-scale network, but their experiment results are
not enough to testify its good performance.
MCNH is actually a minimum-cost satisfiability
problem (MinCostSAT). MinCostSAT, as a Boolean
Satisfiability (SAT) problem, is to minimize the cost
of the satisfying assignment, and is suitable for
Automatic Test Pattern Generation (ATPG), FPGA
Routing, AI Planning, etc. (Fu, 2006). (Li, 2004)
have done in-depth research on optimization
algorithms for the MinCostSAT in his PhD thesis.
However, these algorithms for the MinCostSAT is
not suitable for the minimum-cost network
hardening problem.
3 SLOS
SLOS is come from Stochastic Loose Optimize
Principle (SLOP). If a set named Universe is
partitioned to 2 parts: Low and High, and the ratio of
element numbers of Low and Universe is P
L
, then,
the probability of an element selected stochastically
from the Universe belongs to Low is P
L
, and to High
is 1-P
L
. If repeat the selection N times, then, the
probability of selected an element from the Low is
1-(1-P
L
)N. No matter how many elements in the
Universe, and how tiny the P
L
is, we can ensure the
probability of the above selection success is close
enough to 1, as long as the N is moderate big.
As Figure 1 shown, the proof of SLOP is very
simple.
Premise:
|Low|/|Universe| = P
L
;
r
1
, r
2
, … , r
N
∈ Universe;
r
1
, r
2
, … , r
N
is an array of random numbers.
Conclusion:
P({ r
1
, r
2
, … , r
N
}∩Low≠∅) = 1-(1-P
L
)
N
,
where P(event) means the probability of the event happens.
Proof:
∵ r
1
, r
2
, … , r
N
∈ Universe, and they are random numbers.
∴ P(r
1
∈ Low) = P(r
2
∈ Low) = … = P(r
N
∈ Low) = P
L
.
∴ P(r
1
∉ Low) = P(r
2
∉ Low) = … = P(r
N
∉ Low) = 1-P
L
.
and, ∵ the set of events r
1
∉ Low, r
2
∉ Low, … , r
N
∉ Low are
stochastic independence.
∴ P({ r
1
, r
2
, … , r
N
}∩Low =∅)
= P((r
1
∉ Low)∩(r
2
∉ Low)∩…∩(r
N
∉ Low))
= P(r
1
∉ Low)×P(r
2
∉ Low) ×…×P(r
N
∉ Low)
= (1-P
L
)
N
∴ P({ r
1
, r
2
, … , r
N
}∩Low≠∅)
= 1- P({ r
1
, r
2
, … , r
N
}∩Low =∅)
= 1- (1-P
L
)
N
.
Figure 1: Proof of the stochastic loose optimize principal.
SLOS is a strategy for state space searching
which could be used to find an approximate solution
Self-ad-MCNHA-SLOS - A Self-adaptive Minimum-Cost Network Hardening Algorithm based on Stochastic Loose
Optimize Strategy
373

of NP-hard problem quickly. The basic idea is:
select an array of states from the whole state space
to form a stochastic state sub-space, named Sparse-
Space, and the distance between the optimal state of
the Sparse-Space and the optimal state of the whole
space will become smaller gradually with the scale
of the Sparse-Space increasing, according to
concerned partial order. If the scale of the whole
state space is too large to be traveled in limited time,
SLOS could be used to find an approximate optimal
state in a Sparse-Space, and the approximate optimal
state is better and better with the scale of Sparse-
Space increasing. That is, we could find an
approximate solution of a NP-hard problem in a
Sparse-Space with moderate scale, when computing
resource is limited.
MCNH comes down to a state space searching
problem with double constraint conditions, that is,
the Opt-Plan must be both validity and with
minimum cost. The validity depends on the plan
itself, while, the judgment of the minimality need to
search the hardening plan space. We used the SLOS
iteratively both in the MNCHA-SLOS and the Self-
ad-MCNHA-SLOS to ensure the Approx-Opt-Plan’s
validity and approximate minimality.
Table 1: Symbols and their meanings.
Plan
Network Hardening Plan
Approx-Opt-Plan
Approximate Optimal Plan
Opt-Plan
Optimal Plan
Plan-Space
Network Hardening Plan Space
Sparse-Space
Subspace of the Plan-Space contains Some
Stochastic Plans
Valid-Space
Subspace of the Plan-Space contains all of
the Valid Plans
Superior-Space
Subspace of the Plan-Space contains those
Superior Plans
Goal-Space
Subspace of the Plan-Space contains those
Plans both Valid and Superior
Rand()
Random number generator
Valid()
A Function to judge the Validity of Plan
Cost()
A Function to compute the cost of Plan
GeneratePlan()
Plan Generator
density
Mathematical Expectation of the 1-density of
Plan
UpdateDensity()
The Updater of the density
NSparse
The Scale of Sparse-Space
Niterate
Iterate times
PValid
The Ratio of Valid plans
PSuperior
The Ratio of Superior plans
PGoal
The Probability of the Approx-Opt-Plan in
Goal-Space
4 MCNHA-SLOS
4.1 Basic Appointments and Concepts
Appointment 1. The costs of network hardening
plans are given.
Appointment 2. The hardening plan space (Plan-
Space) and hardening plan’s validity judgment
function (Valid()) are given.
Appointment 3. Symbols used in this article with
their meanings in Table. 1.
4.2 Algorithm Description
Basic Thought. Use the SLOS iteratively to meet the
two measures: minim-cost and validity, select the
minimum-cost Plan, noted as Min-Plan, in a N
Sparse
scale Sparse-Space in every iteration, and update the
Approx-Opt-Plan according to the Min-Plan’s
validity, ensure the probability of the Approx-Opt-
Plan belongs to the Goal-Space is close to 1 by
N
iterate
times iterations. It could be easily proved that
the probability of the Approx-Opt-Plan belongs to
the Goal-Space is P
Goal
, as formula (1) shown, by
N
iterate
times of iterations on N
Sparse
scale Sparse-
Spaces.
(1 (1 ) ) (1 (1 ) )
Sparse
iterate
N
N
Goal Superior Valid
P P P
(1)
The pseudo-code of the MCNHA-SLOS is shown in
Figure 2.
Figure 2: Pseudo-code of the MCNHA-SLOS.
4.3 Algorithm Analysis
It is obvious that accurate solving the MCNHP need
to search the whole Plan-Space to find the Opt-Plan,
and the theoretical complexity is 2
n
, while, the
MCNHA-SLOS only need N
iterate
×N
Sparse
times
checking to ensure the Approx-Opt-Plan meet the
user’s expectation, as formula (1) shown. If the scale
of the Plan-Space n is moderate big, those accurate
solving method will inevitable failure, under the Von
Begin:
Approx-Opt-Plan ← 2
n
-1;
for round = 1 to N
iterate
;
Min-Plan ← Approx-Opt-Plan;
for count = 1 to N
Sparse
;
Plan = Rand(t)%2
n
;
if( Cost(Plan) < Cost(Min-Plan) )
Min-Plan ← Plan;
if( Valid(Min-Plan) )
Approx-Opt-Plan ← Min-Plan;
Output: Approx-Opt-Plan;
End.
SECRYPT 2012 - International Conference on Security and Cryptography
374

Neumann architecture. While, according to formula
(1), P
Valid
is fixed for a given goal of a given network,
P
Superior
is given by user, therefore, no matter how
tiny the P
Superior
and the P
Valid
, there are moderate
N
iterate
and N
Sparse
to ensure the P
Goal
is close to 1,
unless the Goal-Space is empty. We can also find
from the formula (1) that the N
Sparse
is mainly to
control the distance between the Approx-Opt-Plan
and Opt-Plan, while, the N
iterate
is mainly to ensure
the validity of the Approx-Opt-Plan.
Generally speaking, the MCNHA-SLOS
transforms the accurate problem solving of 2
n
scale
to approximate problem solving of N
iterate
×N
Sparse
scale, and transforms an couldn’t accomplishable
problem of finding the optimal solution in limited
time to an accomplishable problem of finding a
satisfying approximate optimal solution in limited
time, and is able to control the precision of the
solving process according to the available
computing resource and the user’s expectation.
5 Self-ad-MCNHA-SLOS
According to a mass of experiments, we find some
interesting phenomenon. Given a network and a goal,
if fix the N
iterate
, the probability of the Approx-Opt-
Plan is nontrivial valid reducing with the N
Sparse
increasing; if give N
Sparse
a relative big or tiny value,
the changing of N
iterate
has not significant impact on
the probability of the Approx-Opt-Plan is nontrivial
valid, however, if give N
Sparse
a suitable value, the
impact will be significant, and the suitable values of
the N
Sparse
for different goals are various.
For a given network and a given goal, the
probability of a stochastically selected Plan has a
positive correlation relationship with the 1-density
of its binary representation, that is, the more
vulnerabilities of a Plan contains, the higher of the
probability of the Plan is valid, besides, those valid
Plans definitely have a 1-density lower bound, since
the Plan (0)
2
is invalid for any goal of any network.
The increasing of N
Sparse
, actually, is reducing the
probability of those Min-Plans selected from each
Sparse-Space, because the cost of a Plan also has a
positive correlation relationship with the 1-density
of the Plan’s binary representation. When the N
Sparse
becomes big enough, those Min-Plans will be
invalid with high probability, therefore, the impact
of the increasing of N
iterate
to the probability of the
Approx-Opt-Plan is valid will be insignificant.
If we could find the suitable N
Sparse
quickly for
different goals in different networks, it will
significantly improve the efficiency of the MCNHA-
SLOS, however, the N
Sparse
is a relative stable
number mainly used to control the computation
complexity. Fortunately, we find a substitutable way
to adjust the 1-density of Sparse-Spaces according to
the history validity statistic of those Min-Plans to
make sure the sequence of Sparse-Spaces are
convergent to the Opt-Plan. There are still two
important problems to address, one is how to
generate those Sparse-Spaces according to different
required 1-density, and the other is how to update
the 1-density according to the history validity
information of those Min-Plans. Intuition tell us, if
Min-Plans are valid continuously, we should lower
the 1-density, while, if Min-Plans are invalid
continuously, we should increase the 1-density, and
the lower’s preconditions should be weaker than the
increase’s, since we want to got the minimum-cost
valid Plan.
Based on the above considerations, we proposed
Self-ad-MCNHA-SLOS shown in Figure 3,
Compared with the MCNHA-SLOS, it add a special
function GeneratePlan(density) to generate
stochastic Plans and a function UpdateDensity() to
adjust the density dynamically in each iteration,
where the density is the parameter to control the 1-
density of Plans of GeneratePlan(density) generated,
and its range is (0,1] and is assigned 0.9 to be its
initial value.
Figure 3: Pseudo-code of the Self-ad-MCNHA-SLOS.
GeneratePlan(density) is defined as formula (2). If
fixed the density to 0.5, it will become Rand(t)%2
n
as in MCNHA-SLOS.
1 2 2
( , ) ( ... ) ,
1 ( )%10 10,
,
0 ( )%10 10.
, ( 1) .
n
i
Sparse
GeneratePlan t density x x x
if Rand t density
where x
if Rand t density
where t round N i
(2)
And we define the UpdateDensity() as formula (3),
where the upFlag is to record the count of those
Min-Plans continuously invalid and the downFlag is
to record the count of continuously valid, and both
Begin:
Approx-Opt-Plan ← 2
n
-1;
density = 0.9;
for round = 1 to N
iterate
;
Min-Plan ← Approx-Opt-Plan;
for count = 1 to N
Sparse
;
Plan = GeneratePlan(density)
if( Cost(Plan) < Cost(Min-Plan) )
Min-Plan ← Plan;
if( Valid(Min-Plan) )
Approx-Opt-Plan ← Min-Plan;
density = UpdateDensity();
Output Approx-Opt-Plan;
End.
Self-ad-MCNHA-SLOS - A Self-adaptive Minimum-Cost Network Hardening Algorithm based on Stochastic Loose
Optimize Strategy
375

of them are assigned 0 to be their initial value.
Where the UpTraction and DownDrang are the
upper limit of the upFlag and the downFlag
respectively, if any one of the two variables reached
its upper limit, the density will be updated according
to the formula (3), and both of the two variables will
be assigned 0 again. Generally speaking, the upFlag
like a traction to increase the density, while the
downFlag like a drang to lower the density, and the
direction of the state space searching could be
dynamically adjusted by suitable UpTraction and
DownDrang.
, , ,()
0.1 ,
0.1 .
upFlag UpTraction downFlag DownDrangUpdateDensity
density if upFlag UpTraction
density if downFlag DownDrang
(3)
6 EXPERIMENT
To testify and evaluate algorithms proposed above,
we generate simulative networks and build their
attack graphs using our Network Modeling and
Demonstrating System (Net-MDs) and Network
Vulnerability Analyzing System (Net-VAs), as
Figure 4 and Figure 5 shown. To be concise, we
assigned every vulnerability’s remedy cost 1,
therefore, the cost of hardening plan only depend on
the total vulnerabilities it contains. Besides, as
shown in Figure 4, the single target refers to the
server circled by the bold red loop, and the multiple
targets refers to 4 servers circled by red loops.
Figure 4: Simulative network generated by Net-MDs.
Figure 5: Attack Graph Generated by Net-Vas.
We designed a series of experiments to analyze
the parameters of the Self-ad-MCNHA-SLOS for
finding the best parameter setting principles, and
compared and evaluated the traits and performance
of the MCNHA-SLOS and the Self-ad-MCNHA-
SLOS (see Appendix). In the end, We find: 1.
UpTraction(N
iterate
/e), DownDrang(1) and N
Sparse
(7)
are good parameters for Self-ad-MCNHA-SLOS; 2.
Self-ad-MCNHA-SLOS can significantly improve
MCNHA-SLOS’s performance.
We also compared the Self-ad-MCNHA-SLOS
with (Feng Chen, 2009)’s approximate method
weighted-Greedy in same environment, since those
accurate methods aren’t able to deal with large-scale
network, radically. Due to the complicity of the
weighted-Greedy is firmed as |C|×|L| for a given
goal and given n-valid attack path length n, where C
denotes all of the initial attributes and L denotes all
of the n-valid attack path, we assign appropriate
values to N
iterate
to ensure that N
iterate
×N
Sparse
approximate to |C|×|L| for the purpose of comparing
the accuracy of the two approximate hardening plans:
Greedy-Plan and Approx-Opt-Plan. We observe the
costs of the two approximate plans, respectively, in
four simulated networks: Net
1
with 200 nodes and
10 vulnerabilities, Net
2
with 200 nodes and 20
vulnerabilities, Net
3
with 200 nodes and 30
vulnerabilities and Net
4
with 200 nodes and 40
vulnerabilities.
Figure 6: Comparison of the Self-ad-MCNHA-SLOS and
the weighted-greedy.
As Figure 6 shown, the cost of Greedy-Plan is
lower than the average cost of Approx-Opt-Plans
when network scale is small but significant bigger
when network scale is moderate big. Besides, the
average cost of Approx-Opt-Plans generated by Self-
ad-MCNHA-SLOS relative stable while the cost of
Greedy-Plan generated by weighted-Greedy increase
obviously with the network scale, on condition that
the Self-ad-MCNHA-SLOS spends equivalent
computing resource with the weighted-Greedy. The
above results illustrate that the Self-ad-MCNHA-
SLOS is more efficient than the weighted-Greedy,
especially when facing large-scale network.
According to the above experiments, the Self-ad-
MCNHA-SLOS could make those Sparse-Spaces
converge quickly to the Opt-Plan by adjusting the
SECRYPT 2012 - International Conference on Security and Cryptography
376

parameter density, therefore, it could get an Approx-
Opt-Plan very close to the Opt-Plan by limited
amount of searches in the Plan-Space. The merits of
high-efficiency, controllable, and asymptotically
optimal, ensure that it could make full use of
available computing resource to find possible better
result, therefore very suitable for large-scale network.
7 CONCLUSIONS
In this paper, we proposed the Self-ad-MCNHA-
SLOS to address the MCNH problem using SLOS
and self-adaptive parameter adjust strategy. It could
find an approximate optimal hardening plan close
enough to the optimal hardening plan by limited
amount of searches, and has the merits of high-
efficiency, controllable and asymptotically optimal,
therefore, can make full use of available computing
resource to find possible better result, and is very
suitable for large-scale network environment.
Considering the Self-ad-MCNHA-SLOS’ ability of
transforming NP-hard problem to P-hard iterations,
we will study the generalization of the algorithm to
solve more hard problems in future.
ACKNOWLEDGEMENTS
This paper is supported by the National High
Technology Research and Development Program of
China (863 Program) under Grant
No.2009AA01Z432, the National Natural Science
Foundation of China under Grant No.60873215 and
the Hunan Provincial Natural Science Foundation of
China under Grant No.s2010J5050.
REFERENCES
S. Jha, etc., 2002. Two Formal Analyses of Attack Graphs.
In CSFW’02, 15th IEEE Computer Security
Foundations Workshop.
Steven Noel, etc., 2003. Efficient Minimum-Cost Network
Hardening Via Exploit Dependency Graphs. In
ACSAC’03, 19th Annual Computer Security
Applications Conference.
Lingyu Wang, etc., 2006. Minimum-Cost Network
Hardening Using Attack Graphs. Computer
Communications, Vol. 29, Issue 18, pp. 3812--3824.
John Homer, etc., 2008. From Attack Graphs to
Automated Configuration Management - An Iterative
Approach. Kansas State University Technical Report.
Feng Chen, etc., 2008. An Efficient Approach to
Minimum-Cost Network Hardening Using Attack
Graphs. In IAS’2008, 4th International Conference on
Information Assurance and Security.
Laura P. Swiler, etc., 2001. Computer-Attack Graph
Generation Tool. In DISCEX’01, DARPA Information
Survivability Conference &Exposition II.
Oleg Sheyner, etc., 2002. Automated Generation and
Analysis of Attack Graphs. In S&P’ 02, IEEE
Symposium on Security and Privacy.
Paul Ammann, etc., 2002. Scalable, Graph-Based Network
Vulnerability Analysis. In CCS’02, 9th ACM
conference on Computer and communications
security.
R. P. Lippmann, etc., 2005. Evaluating and Strengthening
Enterprise Network Security Using Attack Graphs.
Technical Report, MIT Lincoln Laboratory.
Xinming Ou, etc., 2005. MulVAL: A logic-based network
security analyzer. In 14th USENIX Security
Symposium.
Xinming Ou, etc., 2006. A scalable approach to attack
graph generation. In CCS’06, 13th ACM conference on
Computer and communications security.
Kyle Ingols, etc., 2006. Practical attack graph generation
for network defense. In ACSAC’06, 22nd Annual
Computer Security Applications Conference.
Feng Chen, etc., 2009. Two Scalable Approaches to
Analyzing Network Security Using Compact Attack
Graphs. In IEEC'09, International Symposium on
Information Engineering and Electronic Commerce.
Vaibhav Mehta, etc., 2006. Ranking attack graphs. In
RAID’06, Recent Advances in Intrusion Detection .
Richard Lippmann, etc., 2007. An interactive attack graph
cascade and reachability display. In VizSEC ’07, IEEE
Workshop on Visualization for Computer Security.
J. Homer, etc., 2008. Improving attack graph visualization
through data reduction and attack grouping. In
VizSEC’08, 5th International Workshop on
Visualization for Cyber Security.
Zhaohui Fu, etc., 2006. Solving the minimum-cost
satisfiability problem using sat based branch and
bound search. In ICCAD’06, International Conference
on Computer-Aided Design.
Xiaoyu Li, 2004. Optimization Algorithms for the
Minimum-Cost Satisfiability Problem. PhD thesis,
North Carolina State University.
Self-ad-MCNHA-SLOS - A Self-adaptive Minimum-Cost Network Hardening Algorithm based on Stochastic Loose
Optimize Strategy
377
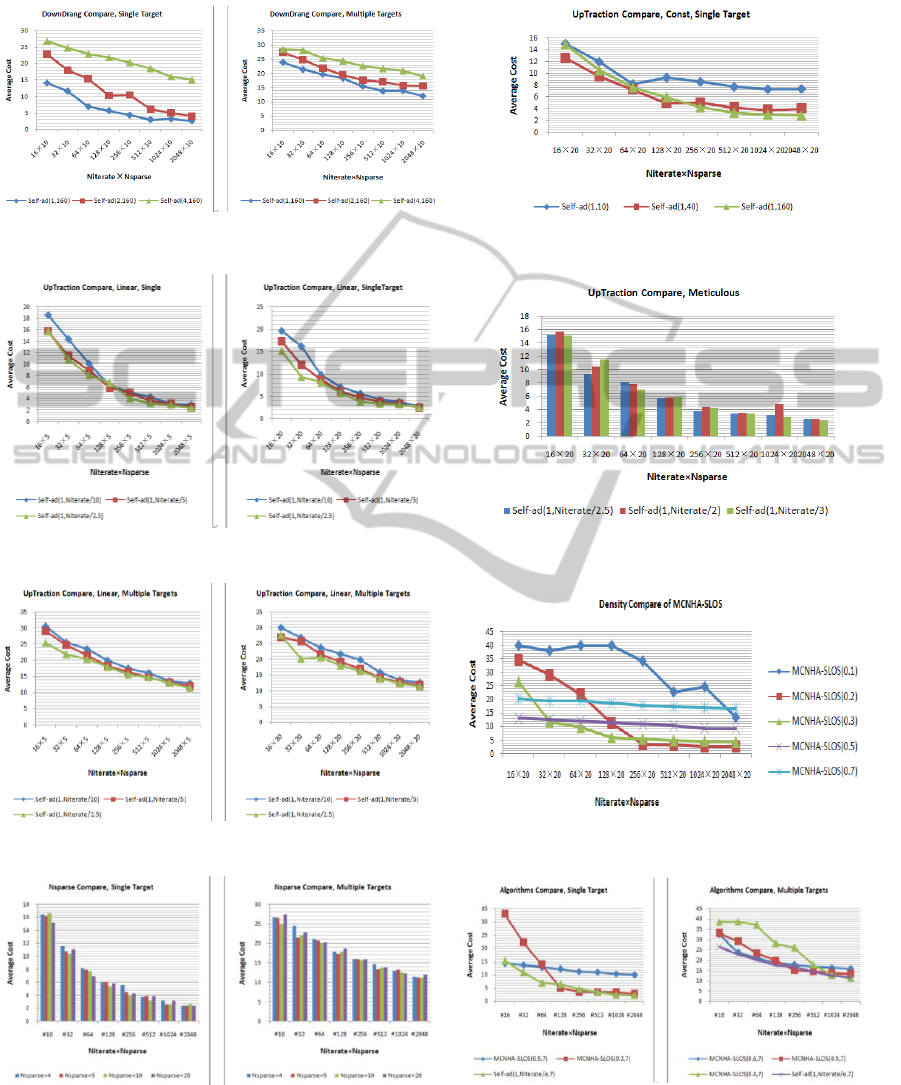
APPENDIX
Figure A1: Comparison of DownDrang.
Figure A2: Comparison of UpTraction.
Figure A3: Comparison of ratios.
Figure A5: Comparison of ratios, meticulously.
Figure A4: Comparison of ratios.
Figure A7: Comparison of density.
Figure A6: Comparison of NSparse.
Figure A8: Algorithms comparison.
SECRYPT 2012 - International Conference on Security and Cryptography
378
