Performance Analysis of New SNR Estimation Methodology based on

Preamble Approach

Sangmi Moon, Saransh Malik, Bora Kim, Cheolhong Kim and Intae Hwang

Department of Electronics and Computer Engineering, Chonnam National University,

300 Yongbong-Dong, Buk-Gu, Gwangju, Republic of Korea

Keywords: CSI, MIMO, OFDM, Preamble, SNR.

Abstract: The latest wireless communication systems focus on developing MIMO-OFDM systems that allow the

transmission of very high data rates in fading environments. We can optimize these systems even further by

setting the modulation and coding adaptively according to the channel conditions, and by using sub-carrier

frequency and power allocation techniques. The overall system performance depends on the accuracy and

delay of the channel state information (CSI). In this paper, we propose a signal-to-noise ratio (SNR)

estimation algorithm based on preamble transmission. Through simulations of several channel environments,

we prove that our proposed algorithm is more accurate than conventional algorithms.

1 INTRODUCTION

Adaptive modulation and coding (AMC), adaptive

subcarrier allocation, and power allocation are used

to increase the system's reliability and transmission

rate. These techniques require feedback of the

channel state information (CSI), which is based on

the estimated SNR of the received signal. Therefore,

many studies have been conducted to improve the

system performance by designing a low complexity

SNR estimation algorithm (Pauluzzi and Beaulieu,

2000); (Xu et al., 2005); (Jiao et al., 2008);

(Boumard, 2003); (Ren et al., 2009); (Zivkovic and

Mathar, 2009). Previously, conventional SNR

estimation algorithms were based on the maximum

likelihood (ML) or minimum mean squared error

(MMSE) and required an estimation of the channel,

which entails feedback delay and higher

computational cost. Recently, some researchers such

as Boumard, Ren and Milan proposed estimating the

SNR based on preamble transmission without

channel estimation. Our proposal consists of using

the preamble principle to diminish the complexity

and feedback delay and avoid channel estimation.

Because the preamble is known by both sides of the

transceiver, the new algorithm can accurately the

follows. In section 2, we present the system model,

and in section 3, we briefly explain the conventional

SNR estimation algorithms proposed by Boumard,

Ren, and Milan, as well as the new proposed SNR

estimation algorithm. In section 4, we analyze and

compare the simulated performance of each of the

algorithms. Finally, in section 5, we present our

conclusions.

2 SYSTEM MODEL

In this section, we explain the structure of the

communication system. As shown in Figure 1, only

two signals with two respective preambles are

transmitted. The two transmission and two receiver

antennas make up a 2

2 multiple-input multiple-

output (MIMO)-orthogonal frequency division

multiplexing (OFDM) system. At the receiver, the

SNR is estimated after the received signal is

changed from the time domain to the frequency

domain using fast Fourier transform (FFT). The

timing of the received signal is assumed to be

perfectly synchronized.

2.1 Transmitter

Each antenna transmits an OFDM symbol,

consisting of a sequence of a predetermined number

(OFDM size) of binary phase shift keying (BPSK)

or quadrature phase shift keying (QPSK) symbols.

The preamble is thus composed of these two

identical OFDM symbols. In Figure 1, the preamble

is given by C

(k, n), where, i = 1, 2 represents the

115

Moon S., Malik S., Kim B., Kim C. and Hwang I..

Performance Analysis of New SNR Estimation Methodology based on Preamble Approach.

DOI: 10.5220/0004026801150119

In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems

(SIGMAP-2012), pages 115-119

ISBN: 978-989-8565-25-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

transmit antenna index, k = 1, 2 is the preamble

index, and n = 0, ..., N-1 is the subcarrier index. For

preamble transmission, we used a cyclic prefix (CP)

of length N/4 as the guard interval.

2.2 Receiver

The received signal after FFT processing is

described by equation (1):

() ()() ()

∑

,,,,

jiijj

nknnkCnkHnkY

(1)

where Y

(k, j) is the signal received at the jth

antenna, and n

(k, n) is the additive white Gaussian

noise (AWGN) present at the input of the jth receive

antenna. H

(k, n) indicates the channel frequency

response between the ith transmission antenna and

the jth receiver antenna. It can be expressed

according to equation (2),

() ()

∑

−

sijlij

ijl

ekThnkH

(2)

where h

l, ij

(k, T

) and τ

l, ij

represent the lth path gain

and delay, respectively, between the ith transmission

and jth receiver antenna during the kth preamble. T

is the OFDM preamble time plus CP, and L is the

number of channel paths. In this paper, the channel

is assumed to be constant during a frame period.

Therefore, for simplicity, the time k is not taken into

account for SNR estimation.

Figure 1: Block diagram of the preamble-based 2×2.

3 CONVENTIONAL SNR ESTIMA

TION ALGORITHMS

3.1 Boumard’s SNR Estimation

Algorithm

According to the Boumard algorithm, in a 2×2

MIMO-OFDM system, the channel varies slowly in

both the frequency and time domains; with this

assumption, two identical consecutive preambles are

used to estimate the SNR (Boumard, 2003). The

signal power is estimated as follows. First, we

estimate Ĥ using equation (3), which is a function of

the two received signals Y(0, n) and Y(1, n), and the

transmitted preamble C(n). Next, we calculate the

average of the squares of the absolute values of Ĥ

using equation (4). The noise power is estimated

using equation (5), and finally, the SNR is estimated

using equation (6). Unlike ML or MMSE-based

SNR estimation, Boumard’s algorithm does not

require channel estimation, but large changes in the

channel can lead to errors in the SNR estimate.

()

∑

−

Bou

(3)

()

()()()

nYnY

nH ,1,0

(4)

()()()()

()( )( )()

∑

−

−+−−−

+−

1,11,01

,1,01

Bou

nYnYnC

(5)

Bou

Bouav

(6)

3.2 Ren’s SNR Estimation Algorithm

Ren’s SNR estimation overcomes the weakness of

Boumard’s regarding frequency selective channels

by using the same subcarrier in the noise power

estimation [equation (7)] (Ren et al., 2009). The

signal power is estimated by equation (8), where the

estimated noise power is removed from the total

received signal power. As in Boumard’s algorithm,

Ĥ is estimated by equation (3), and finally, we

calculate the SNR with equation (9).

()()()

()

∑

−

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

,0,0

nHnCnY

(7)

()

∑

−

−=

WnY

(8)

nav

Re,

(9)

3.3 Milan’s SNR Estimation Algorithm

The preamble used in Milan’s SNR estimation

algorithm contains periodic identical parts in the

time domain (Zivkovic and Mathar, 2009). Figure

2(a) shows the structure of the preamble in the time

domain. N subcarriers are divided into Q identical

parts. Figure 2(b) shows the preamble structure in

the frequency domain. Q signal subcarriers appear

periodically between the null subcarriers. Milan’s

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications

116

algorithm uses these characteristics to estimate the

SNR. After the received signal is FFT modulated

(with an FFT size equal to the total preamble

duration, i.e., 128), the signal power is contained in

the Q signal subcarriers, and the noise power is

contained in the null subcarriers of the received

signal. As we can see in reference (Pauluzzi and

Beaulieu, 2000), Milan’s algorithm provides more

accurate estimations by reducing the interval period;

however, the preamble structure becomes more

complicated. In our system, we transmit two equal

OFDM symbols of size N = 64, which is the

preamble length corresponding to Milan’s algorithm

for the case of N = 128 and Q = 2. However, in our

algorithm we need an FFT size of only 64 at the

receiver, whereas Milan’s algorithm requires an FFT

size of 128.

Figure 2: Preamble structure of Milan’s algorithm. (a)

Time domain, (b) frequency domain.

3.4 New SNR Estimation Algorithm

Figure 3 shows the structure of the transmission

frame, including the preamble. Equation (10) is the

new expression for estimating the SNR, where Y(0,

n) and Y(1, n) represent the consecutive receive

preambles after FFT.

Figure 3: Transmit preamble structure in the new SNR

estimation algorithm.

()()

⎟

⎠

⎞

⎜

⎝

⎛

−

∑

Newav

nYnY

,1,0

(10)

According to equation (10), the signal power is

considered to be the total power carried by the

preambles, i.e., the noise power is calculated by the

average of the square of the absolute values of the

received preambles.

4 PERFORMANCE ANALYSIS

OF THE PROPOSED AND

CONVENTIONAL SNR

ESTIMATION ALGORITHMS

In this section, we present the performance analysis

of the proposed and conventional SNR estimation

algorithms. Table I and Table II contain the

simulation and channel parameters, respectively.

The simulation parameters are based on IEEE

Standard 802.11n; they include 20 MHz of

bandwidth and MIMO-OFDM as the simulation

platform. The SNR is estimated by considering only

two consecutive preambles with the OFDM symbol

size and BPSK or QPSK modulation. We performed

simulations over three different channels: the

Rayleigh flat fading channel, where the channel

conditions change only slightly; Rayleigh selective

fading channel A, where the maximum delay of the

samples is shorter than the CP; and Rayleigh

selective fading channel B, where the maximum

delay of the samples is longer than the CP.

∑

⎟

⎠

⎞

⎜

⎝

⎛

−

aviav

NMSE

ρρ

(11)

where N

is the number of transmitted packets

(25,000),

is the estimated SNR value

corresponding to the received preamble from the ith

package, and ρ

represents the actual SNR value.

Figure 4 compares the actual SNR values and those

estimated by each algorithm over the Rayleigh flat

fading channel. At low SNRs, the Ren algorithm has

a higher SNR estimation error than the other

algorithms, which return values almost identical to

the actual SNR. Figure 5 shows the NMSE

performance for each algorithm. We can verify that

Boumard’s and the new SNR algorithm provide the

most accurate estimations, with NMSE values close

to 0, followed by Milan and Ren. As mentioned in

the description above, for Boumard’s algorithm the

channel is considered to be almost stationary. The

performance results, confirm that the most suitable

algorithms for these conditions are Boumard’s and

the new SNR estimation algorithm. Figure 6

compares the actual and estimated SNR values over

Rayleigh selective fading channel A.

The estimation error of Boumard’s algorithm

increases for a selective channel. Figure 7 shows the

NMSE performance on the same channel. For

Boumard’s algorithm, the NMSE increases with the

SNR, whereas Milan’s and Ren’s algorithms

maintain a constant NMSE value of about 0.3

PerformanceAnalysisofNewSNREstimationMethodologybasedonPreambleApproach

117

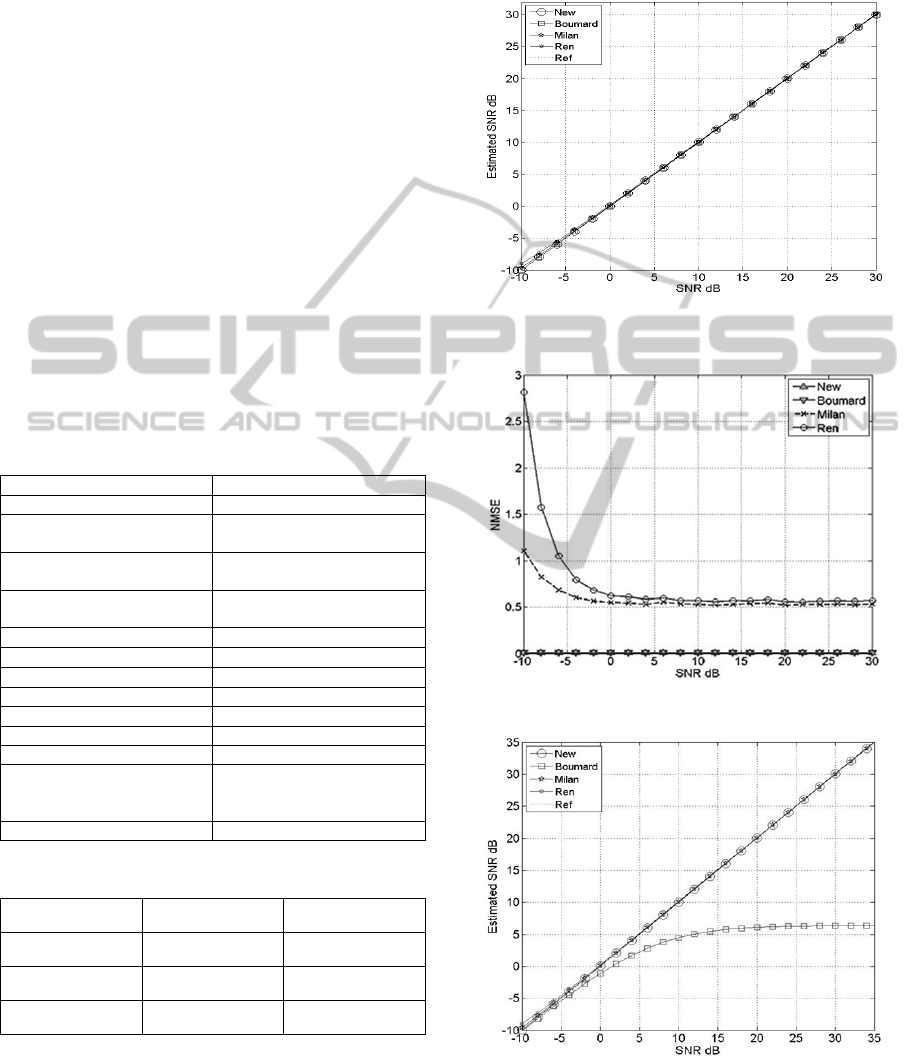
starting at approximately 0 dB. The NMSE of the

new algorithm is very close to 0, which means that

for a frequency selective multi-path channel, the

new algorithm provides the most reliable estimation

of the real SNR value. Figure 8 and Figure 9 show

the result of the same simulations over Rayleigh

selective fading channel B, where the maximum

delay is larger than the CP length, using four

multiple paths. This channel environment is more

difficult than channel A; therefore, each algorithm

has a higher estimation error than in the previous

simulation of channel A. In Figure 8, the values

estimated by Boumard’s algorithm are very far from

the actual SNR values, whereas those estimated by

the new algorithm, as the values estimated by

Boumard’s algorithm are very far from the actual

SNR values, while those estimated by the new

algorithm, as well as by those of Milan and Ren,

remain very close to the actual value until

approximately 26 dB. Furthermore, Figure 9 shows

that until approximately 38 dB, the new algorithm

has the lowest estimation error.

Table 1: Simulation parameters.

Parameters Value

System bandwidth (BW) 20 MHz

1 OFDM symbol time

4 μs(3.2 μs: FFT length + 0.8

μs: CP length)

Number of data symbols per

space stream(SS)

468

Number of subcarriers per

preamble

Subcarrier spacing 312.5 KHz

MIMO

Layered 2×2

Noise AWGN

FFT length 64 point

GI(CP) length 16 point

1 OFDM symbol samples 80

SNR estimation algorithm Boumard, Milan, Ren, new

Preamble

2 OFDM symbols: 2 equal

sequences of QPSK or

BPSK symbols

Transmission packets 25000

Table 2: Channel parameters.

Channel

Delay

path(samples)

Rayleigh power

Rayleigh selective

fading channel A

3Path:

[0 12 15]

[ -1.92, -5.92,

-9.92 ]

Rayleigh selective

fading channel B

4Path:

[0 12 15 18]

[ -1.92, -5.92,

-9.92, -12.92]

Rayleigh flat

fading channel

No delay -

5 CONCLUSIONS

In this paper, we proposed a new SNR estimation

algorithm that is based on the use of a preamble and

does not require channel estimation to make an

accurate estimation of the SNR.

Figure 4: Actual and estimated SNR values over the

Rayleigh flat fading channel.

Figure 5: NMSE performance over Rayleigh flat fading.

Figure 6: Actual and estimated SNR values over Rayleigh

selective fading channel A.

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications

118

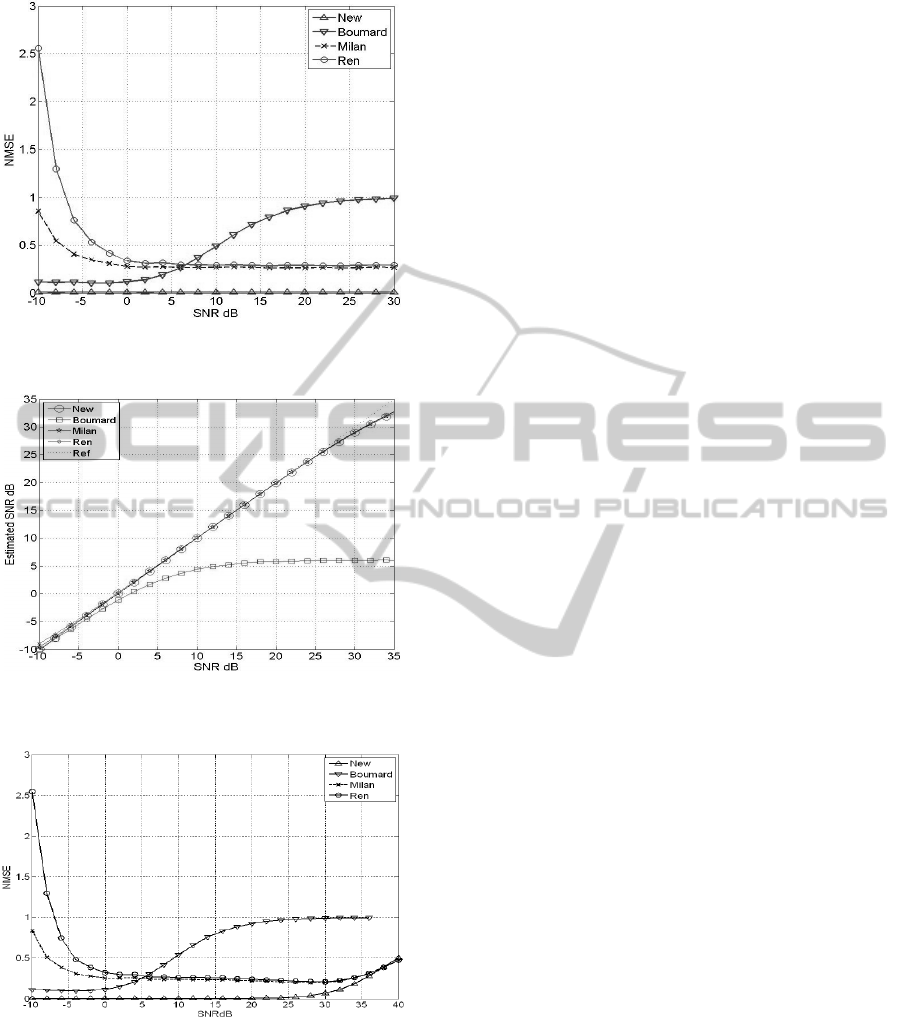
Figure 7: NMSE performance over Rayleigh selective

fading channel A.

Figure 8: Actual and estimated SNR values over Rayleigh

selective fading channel B.

Figure 9: NMSE performance over Rayleigh selective

fading channel B.

In our algorithm, the signal power is considered

to be the entire sequence of two preambles with

OFDM size and composed of BPSK or QPSK

symbols; therefore, we consider the signal power to

be 1. The relative noise power is calculated by the

square of the absolute value of the two received

preambles. By dividing the signal between the noise

power, we obtain the SNR estimation. Simulations

performed in several channels prove that the new

proposed algorithm produces the lowest estimation

error.

ACKNOWLEDGEMENTS

"This research was supported by the MKE(The

Ministry of Knowledge Economy), Korea, under the

ITRC(Information Technology Research Center)

support program supervised by the NIPA(National

IT Industry Promotion Agency)" (NIPA-2012-

H0301-12-3005). "This study was financially

supported by Chonnam National University, 2011".

REFERENCES

D. R. Pauluzzi and, N. C. Beaulieu, “A comparison of

SNR Estimation Techniques for the AWGN Channel,”

IEEE Trans. Commun., vo1.48, pp1681-1691, October

2000.

H. Xu, G. Wei, and J. Zhu, “Novel SNR estimation

algorithm for OFDM,” Proc. IEEE VTC, vol. 5, pp.

3068-3071, June 2005.

F. Jiao, G. Ren, and Z. Zhang, “New Noise Variance and

Post Detection SNR Estimation Method for MIMO

OFDM Systems,” Proc. IEEE Conf. ICCT, pp. 179-

182, Nov. 2008.

S. Boumard, “Novel noise variance and SNR estimation

algorithm for wireless MIMO OFDM systems,” in

Proc. IEEE Global Telecommunications Conf.

(Globecom), vol. 3, pp. 1330-1334, Dec. 2003.

G. Ren, H. Zhang, and Y. Chang, “SNR estimation

algorithm based on the preamble for OFDM systems

in frequency selective channels,” IEEE Trans.

Commun., vol. 57, no. 8, pp. 2230-2234, Aug. 2009.

M. Zivkovic and R. Mathar, “Preamble-based SNR

estimation in frequency selective channels for wireless

OFDM systems,” Proc. of IEEE VTC Spring, pp. 1-5,

2009.

PerformanceAnalysisofNewSNREstimationMethodologybasedonPreambleApproach

119