
Semantic Place Recognition based on Deep Belief Networks and Tiny
Images
Ahmad Hasasneh
1,2
, Emmanuelle Frenoux
1,2
and Philippe Tarroux
2,3
1
Paris Sud University, Orsay, F-91405, France
2
LIMSI-CNRS, B.P. 133, Orsay, F-91403, France
3
Ecole Normale Sup
´
erieure, 45 Rue d’Ulm, Paris, F-75230, France
Keywords:
Semantic Place Recognition, Restricted Boltzmann Machines, Deep Belief Networks, Bag-of-Words, Softmax
Regression.
Abstract:
This paper presents a novel approach for robot semantic place recognition (SPR) based on Restricted Boltz-
mann Machines (RBMs) and a direct use of tiny images. RBMs are able to code images as a superposition of a
limited number of features taken from a larger alphabet. Repeating this process in a deep architecture leads to
an efficient sparse representation of the initial data in the feature space. A complex problem of classification in
the input space is thus transformed into an easier one in the feature space. In this article, we show that SPR can
thus be achieved using tiny images instead of conventional Bag-of-Words (BoW) methods. After appropriate
coding, a softmax regression in the feature space suffices to compute the probability to be in a given place
according to the input image.
1 INTRODUCTION
Robot localization is one of the major problems
in autonomous robotics. Probabilistic approaches
(S. Thrun and Fox, 2005) have given rise to Si-
multaneous Localization and Mapping (SLAM) tech-
niques. However, beyond the precise metric lo-
calization given by SLAM, the ability for a mo-
bile robot to determine the nature of its environment
(kitchen, room, corridor, etc.) remains a challenging
task. View-based approaches achives place recogni-
tion without any reference to the objects present in
the scene. Semantic category can thus be used as con-
textual information which fosters object detection and
recognition (giving priors on objects identity, location
and scale). Moreover, SPR build an absolute refer-
ence to the robot location, providing a simple solu-
tion for problems in which the localization cannot be
deduced from neighboring locations, such as in the
kidnapped robot or the loop closure problems.
2 CURRENT APPROACHES
Current approaches are based on the extraction of ad
hoc features efficient for image coding (gist, CEN-
TRIST, SURF, SIFT) (Oliva and Torralba, 2006; Ul-
lah et al., 2008; Wu and Rehg, 2011). To reduce
the size of these representations, most of the authors
use Bag-of-Words (BoW) approaches which consider
only a set of interest points in the image. This step
is usually followed by vector quantization such that
the image is eventually represented as a histogram.
Discriminative approaches can be used to compute
the probability to be in a given place according to
the current observation. Generative approaches can
also be used to compute the likelihood of an obser-
vation given a certain place within the framework of
Bayesian filtering. Among these approaches, some
works (Torralba et al., 2003) omit the quantization
step and model the likelihood as a Gaussian Mixture
Model (GMM). Recent approaches also propose to
use naive Bayes classifiers and temporal integration
that combine successive observations (Dubois et al.,
2011).
Semantic place recognition then requires project-
ing images onto an appropriate feature space that al-
lows an accurate and rapid classification. Concern-
ing feature extraction, the last two decades have seen
the emergence of new approaches strongly related to
the way natural systems code images (Olshausen and
Field, 2004). These approaches are based on the con-
sideration that natural image statistics are not Gaus-
236
Hasasneh A., Frenoux E. and Tarroux P..
Semantic Place Recognition based on Deep Belief Networks and Tiny Images.
DOI: 10.5220/0004029902360241
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 236-241
ISBN: 978-989-8565-22-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

sian as it would be if they have had a completely ran-
dom structure (Field, 1994). The auto-similar struc-
ture of natural images allowed the evolution to build
optimal codes. These codes are made of statisti-
cally independent features and many different meth-
ods have been proposed to construct them from im-
age datasets. One characteristic of these features is
their locality, that can be related to the notion of re-
ceptive field in natural systems. It has been shown
that Independent Component Analysis (Bell and Se-
jnowski, 1997) produces localized features. Besides
it is efficient for distributions with high kurtosis well
representative of natural image statistics dominated
by rare events like contours; however the method is
linear and not recursive. These two constraints are
released by Deep Belief Networks (DBNs) (Hinton
et al., 2006) that introduce non-linearities in the cod-
ing scheme and exhibit multiple layers. Each layer is
made of a Restricted Boltzmann Machine (RBM), a
simplified version of a Boltzmann machine proposed
by Smolensky (Smolensky, 1986) and Hinton (Hin-
ton, 2002). Each RBM is able to build a genera-
tive statistical model of its inputs using a relatively
fast learning algorithm, Contrastive Divergence (CD),
first introduced by Hinton (Hinton, 2002). Another
important characteristic of the codes used in natural
systems, the sparsity of the representation (Olshausen
and Field, 2004), is also achieved in DBNs.
In (Torralba et al., 2008) the authors have shown
that DBNs can be successfully used for coding huge
amounts of images in an efficient way. Each image in
a very large database is first reduced to a small size
patch (32x32) to be used as an input for a DBN. A set
of predefined features (the alphabet) is computed only
once from a set of representative images and each im-
age is represented by a unique weighted combination
of features taken from the alphabet. With the ap-
propriate parameters, the CD algorithm converges to-
wards a sparse representation of the images. A sparse
code means that an image is represented by the small-
est possible number of features. A simple distance
measurement between the image codes allows com-
paring them. The efficiency of the method shows
that drastically reducing the size of the images pre-
serves a sufficient amount of information for allow-
ing comparisons between them. Thus working with
size-reduced images seems to be a simpler alternative
to the BoW approaches. Since this work seems to
demonstrate that DBNs can be successfully used for
image coding and that tiny images retain enough in-
formation for classification, we have elaborated an ap-
proach based on these considerations and we present
here the obtained results. The main contribution of
this paper is thus the demonstration that DBNs cou-
pled with tiny images can be successfully used in the
context of Semantic Place Recognition (SPR).
3 DESCRIPTION OF THE MODEL
3.1 Gaussian-Bernoulli Restricted
Boltzmann Machines
Unlike a classical Boltzmann Machine, a RBM is a
bipartite undirected graphical model θ={w
i j
,b
i
,c
j
},
linking, through a set of weights w
i j
between visible
and hidden units and biases {b
i
,c
j
} a set of visible
units v to a set of hidden units h (Smolensky, 1986).
For a standard RBM, a joint configuration of the bi-
nary visible units and the binary hidden units has an
energy function, E(v,h,θ) given by:
E(v, h; θ) = −
∑
i, j
v
i
h
j
w
i j
−
∑
i
b
i
v
i
−
∑
j
c
j
h
j
(1)
The probabilities of the state for a unit in one layer
conditional to the state of the other layer can therefore
be easily computed. According to Gibbs distribution:
P(v,h;θ) = −
1
Z(θ)
exp
−E(v,h,θ)
(2)
where Z(θ) is a normalizing constant.
Thus after marginalization:
P(h,θ) =
∑
v
P(v,h;θ) (3)
it can be derived (Krizhevsky, 2009) that the condi-
tional probabilities of a standard RBM are given as
follows:
P(h
j
= 1|v;θ) = σ(c
j
+
∑
i
w
i j
v
i
) (4)
P(v
i
= 1|h;θ) = σ(b
i
+
∑
j
w
i j
h
j
) (5)
where σ(x) = 1/(1 + e
−x
) is the logistic function.
Since binary units are not appropriate for multi-
valued inputs like pixel levels, as suggested by Hinton
(Hinton, 2010), in the present work visible units have
a zero-means Gaussian activation scheme:
P(v
i
= 1|h;θ) ← N (b
i
+
∑
j
w
i j
h
j
,σ
2
) (6)
In this case the energy function of Gaussian-
Bernoulli RBM is given by:
E(v, h; θ) =
∑
i
(v
i
− b
i
)
2
2σ
2
i
−
∑
j
c
j
h
j
−
∑
i, j
v
i
σ
i
h
j
w
i j
(7)
SemanticPlaceRecognitionbasedonDeepBeliefNetworksandTinyImages
237

3.2 Learning RBM Parameters
One way to learn RBM parameters is through the
maximization of the model log-likelihood in a gra-
dient ascent procedure. The partial derivative of the
log-likelihood for an energy-based model can be ex-
pressed as follows:
∂
∂θ
L(θ) = −
∂E(v, θ)
∂θ
data
+
∂E(v, θ)
∂θ
model
(8)
where hi
model
is an average with respect to the model
distribution and hi
data
an average over the sample
data. The energy function of a RBM is given
by E(v,θ) = log
∑
h
exp
−E(v,h,θ)
and ∂E(v,θ)/∂θ =
∑
h
p(h|v;θ)∂E(v,h,θ)/∂θ. Unfortunately, comput-
ing the likelihood needs to compute the partition func-
tion, Z(θ), that is usually intractable. However, Hin-
ton (Hinton, 2002) proposed an alternative learning
technique called Contrastive Divergence (CD). This
learning algorithm is based on the consideration that
minimizing the energy of the network is equivalent to
minimize the distance between the data and a statisti-
cal generative model of it. A comparison is made be-
tween the statistics of the data and the statistics of its
representation generated by Gibbs sampling. Hinton
(Hinton, 2002) showed that usually only a few steps
of Gibbs sampling (most of the time reduced to one)
are sufficient to ensure convergence. For a RBM, the
weights of the network can be updated using the fol-
lowing equation:
w
i j
← w
i j
+ η(hv
0
i
h
0
j
i − hv
n
i
h
n
j
i) (9)
where η is the learning rate, v
0
corresponds to the ini-
tial data distribution, h
0
is computed using equation 4,
v
n
is sampled using the Gaussian distribution in equa-
tion 6 and with n full steps of Gibbs sampling, and h
n
is again computed from equation 4.
3.3 Layerwise Training for Deep Belief
Networks
A DBN is a stack of RBMs trained in a greedy layer-
wise and bottom-up fashion introduced by (Hinton
et al., 2006). The first model parameters are learned
by training the first RBM layer using the contrastive
divergence. Then, the model parameters are frozen
and the conditional probabilities of the first hidden
unit values are used to generate the data to train the
higher RBM layers. The process is repeated across
the layers to obtain a sparse representation of the ini-
tial data that will be used as the final output.
3.4 Description of the Database
We use the COLD database (COsy Localization
Database) (Ullah et al., 2007), which is a collec-
tion of labeled 640x480 images acquired at five
frames/sec during robot exploration of three different
labs (Freiburg, Ljubljana, and Saarbruecken). Two
sets of paths (Standard A and B) have been acquired
under different illumination conditions (sunny, cloudy
and night), and for each condition, one path consists
in visiting the different rooms (corridors, printer ar-
eas, etc.). These walks across the labs are repeated
several times. Although color images have been
recorded during the exploration, only gray images are
used since previous works have demonstrated that in
the case of COLD database colors are weakly infor-
mative and made the system more illumination depen-
dent (Ullah et al., 2007).
As proposed by (Torralba et al., 2008) the image
size is reduced to 32x24 (Figure 1). The final set
of tiny images (a new database called tiny-COLD) is
centered and whitened in order to eliminate order 2
statistics. Consequently the variance in equation 6 is
set to 1. Contrarily to Torralba, the 32x24 = 768 pix-
els of the whitened images are used directly as the
input vector of the network.
Printer Area Corridor Terminal Room
Robotics Lab Printer Area Printer Area
Figure 1: Samples of the initial COLD database. The cor-
responding 32x24 tiny images are displayed bottom right.
One can see that, despite the size reduction, these small im-
ages remain fully recognizable.
4 EXPERIMENTAL RESULTS
4.1 Feature Extraction: The Alphabet
Preliminary trials have shown that the optimal struc-
ture of the DBN in terms of final classification score
is 768−256−128. The training protocol is similar to
the one proposed in (Krizhevsky, 2010) (100 epochs,
a mini-batch size of 100, a learning rate of 0.002, a
weight decay of 0.0002, and momentum). The fea-
tures (Figure 2) computed by training the first layer
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
238

are localized and correspond to small parts of the ini-
tial views like edges and corners that can be identified
as room elements. The combinations of these initial
features in higher layers correspond to larger struc-
tures more characteristic of the different rooms.
Figure 2: A sample of the 32x24 features obtained by
training the first RBM layer on tiny-COLD images. Some
of them represent parts of the corridor which is over-
represented in the database. Some others are localized
edges and corners not specific of a given room.
4.2 Supervised Learning of Places
As previously said, the network giving the best results
is a stack of two RBM networks. The real-valued
output of the second RBM units is used to perform
the classification (Figure 3). Assuming that the non-
linear transform operated by DBN improves the linear
separability of the data, a simple regression method is
used to perform the classification process. To express
the final result as a probability that a given view be-
longs to one room, we normalize the output with a
softmax regression method.
The samples taken from each laboratory and each
different condition of illumination were trained sep-
arately as in (Ullah et al., 2008). For each image
the softmax network output gives the probability of
being in each of the visited rooms. According to
maximum likelihood principles, the largest probabil-
ity value gives the decision of the system. In this case,
we obtain an average of correct answers ranging from
65% to 80% according to the different conditions and
labs as shown in figure 3.
However, two different ways are open for improv-
ing these results. The first one is to use temporal inte-
gration as proposed in (Guillaume et al., 2011). The
second one presented here is to rely on decision the-
ory. The detection rate presented in figure 3 is indeed
computed from the classes with the highest probabil-
ities, irrespective of the relative values of these prob-
abilities. Some of them are close to the chance (in
our case .20 or .25 depending on the number of cat-
egories to recognize) and it is obvious that, in such
cases, the confidence in the decision made is weak.
Thus below a given threshold, when the probability
distribution tends to become uniform, one could con-
sider that the answer given by the system is mean-
ingless. The effect of the threshold is then to discard
the most uncertain results. Figure 4 shows the av-
erage result for a threshold of 0.55 (only the results
where max
X
p(X = c
k
|I) ≥ 0.55, where p(X = c
k
is
the probability that the current view I belongs to c
k
,
are retained). In this case the average rate of accep-
tance (the percentage of considered examples) ranges
from 75% to 80% depending on the laboratory and the
average results show values that outperforms the best
published ones (Ullah et al., 2008). Table 1 shows
an overall comparison of our results with those from
(Ullah et al., 2008) for the three training conditions in
a more synthetic view. It also shows the results ob-
tained using a Support Vector Machine (SVM) classi-
fication instead of softmax. The results are quite com-
parable to softmax showing that the DBN computes a
linear separable signature.
5 DISCUSSION AND
CONCLUSIONS
Our results demonstrate that an approach based on
tiny images followed by a projection onto an appro-
priate feature space can achieve good classification
results in a SPR task. They are comparable to the
most recent approaches (Ullah et al., 2008) based on
more complex techniques (use of SIFT detectors fol-
lowed by a SVM classification). We show that, to
recognize a place, it is not necessary to correctly clas-
sify each image of the place. As the proposed system
computes the probability of the most likely place this
image has been taken from, it offers the way to weight
a view by a certainty factor associated with the prob-
ability distribution over all classes. One can discard
the most uncertain views thus increasing the recogni-
tion score up to very high values. In a place recogni-
tion task not all the images are informative: some of
them are blurred when the robot turns or moves too
fast, some others show non informative details (e.g.
when the robot is facing a wall). Our results offer a
simpler alternative to the method proposed in (Prono-
bis and Caputo, 2007) based on cue integration and
the computation of a confidence criterion in a SVM
classification approach. The second important point
is the use of tiny images that greatly simplifies the
SemanticPlaceRecognitionbasedonDeepBeliefNetworksandTinyImages
239
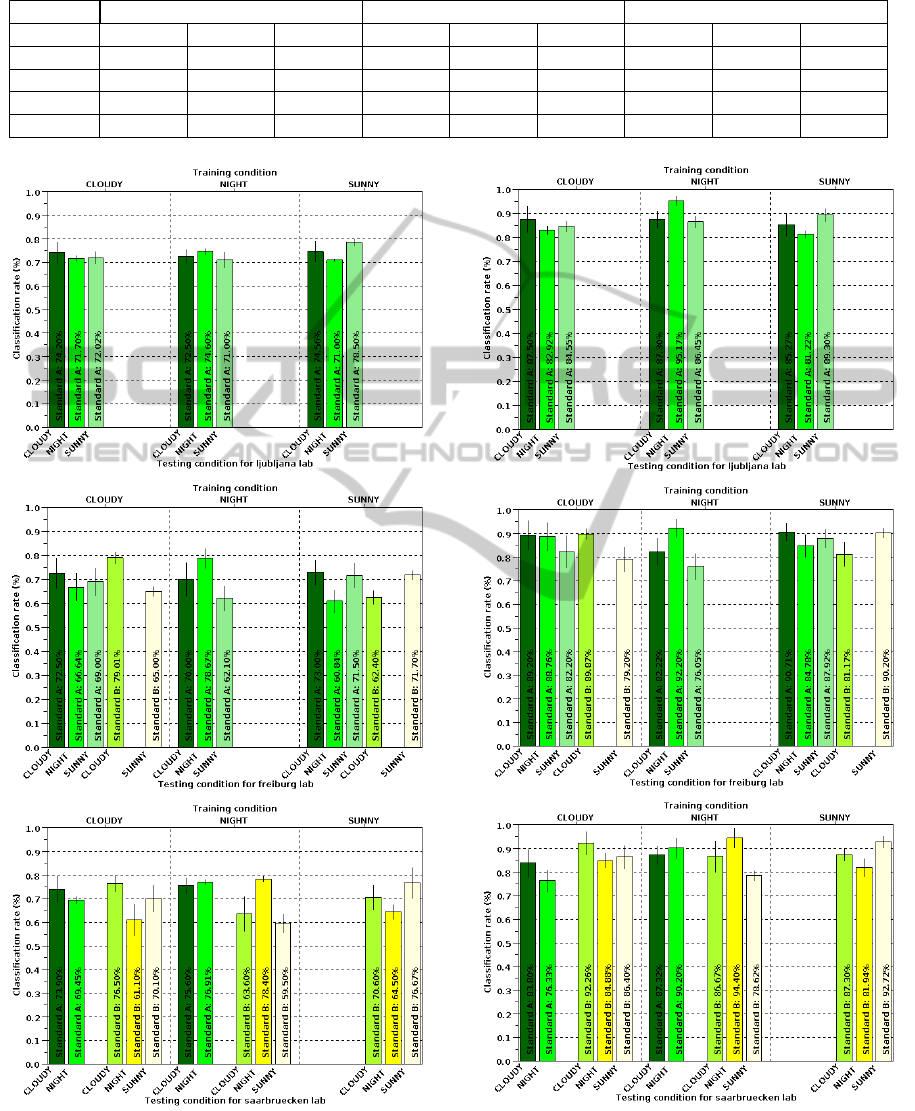
Table 1: Average classification for the three different labs and the three training conditions. First row: Ullah’s work; second
row: rough results without threshold; third row: classification rates with threshold as indicated in text.
Saarbruecken Freiburg Ljubljana
Training Cloudy Night Sunny Cloudy Night Sunny Cloudy Night Sunny
Ullah 84.20% 86.52% 87.53% 79.57% 75.58% 77.85% 84.45% 87.54% 85.77%
No thr. 70.21% 70.80% 70.59% 70.43% 70.26% 67.89% 72.64% 72.70% 74.69%
SVM 69.92% 71.21% 70.70% 70.88% 70.46% 67.40% 72.20% 72.57% 74.93%
0.55 thr. 84.73% 87.44% 87.32% 85.85% 83.49% 86.96% 84.99% 89.64% 85.26%
Figure 3: Average classification from the three different
labs. Training conditions are on top of each set of bar-
charts. Each bar corresponds to a testing condition.
Figure 4: Average classification from the three different
labs with a threshold of 0.55. Same legend as in figure 3.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
240

overall algorithm. The strong size reduction and low
pass filtering of the images lead to perceptual alias-
ing. However this is rather an advantage for seman-
tic place recognition because these images keep only
the most important characteristic of the scene with re-
spect to scene recognition. Concerning the sensitivity
to illumination, our results give similar results as in
(Ullah et al., 2008).
Different ways can be used in further studies to
improve the results. A final step of fine-tuning can
be introduced using back-propagation instead of us-
ing rough features. However, using the rough fea-
tures makes the algorithm fully incremental avoiding
the adaptation to a specific domain. The strict sepa-
ration between the construction of the feature space
and the classification allows considering other classi-
fication problems sharing the same feature space. The
independence of the construction of the feature space
has another advantage: in the context of autonomous
robotics it can be seen as a developmental maturation
acquired on-line by the robot, only once, during an
exploration phase of its environment. Temporal inte-
gration is also a point that deserves to be explored in
future studies. Another point concerns the sparsity of
the obtained code. If we assume that a sparse feature
space increases the linear separability of the represen-
tation, the study of different factors acting on sparsity
would certainly improve the classification score.
So, the present approach obtains scores compara-
ble to the ones based on hand-engineered signatures
(like Gist or SIFT detectors) and more sophisticated
classification techniques like SVM. As emphasized
by (Hinton et al., 2011), it illustrates the fact that fea-
tures extracted by DBN are more promising for image
classification than hand-engineered features.
REFERENCES
Bell, A. J. and Sejnowski, T. J. (1997). Edges are the ’in-
dependent components’ of natural scenes. Vision Re-
search, 37(23):3327–3338.
Dubois, M., Guillaume, H., Frenoux, E., and Tarroux, P.
(2011). Visual place recognition using bayesian fil-
tering with markov chains. In ESANN 2011, Bruges,
Belgium.
Field, D. (1994). What is the goal of sensory coding? Neu-
ral Computation, 6:559–601.
Guillaume, H., Dubois, M., Frenoux, E., and Tarroux, P.
(2011). Temporal bag-of-words - a generative model
for visual place recognition using temporal integra-
tion. In VISAPP, pages 286–295, Vilamoura, Algarve,
Portugal. SciTePress.
Hinton, G. (2002). Training products of experts by mini-
mizing contrastive divergence. Neural Computation,
14:1771–1800.
Hinton, G. (2010). A practical guide to training re-
stricted Boltzmann machines - version 1. Technical
report, Department of Computer Science, University
of Toronto, Toronto, Canada.
Hinton, G., Krizhevsky, A., and Wang, S. (2011). Trans-
forming auto-encoders. In Artificial neural networks
and machine learning - ICANN 2011.
Hinton, G., Osindero, S., and Teh, Y. (2006). A fast learning
algorithm for deep belief nets. Neural Computation,
18:1527–1554.
Krizhevsky, A. (2009). Learning multiple layers of fea-
tures from tiny images. Master sc. thesis, Department
of Computer Science, University of Toronto, Toronto,
Canada.
Krizhevsky, A. (2010). Convolutional deep belief networks
ocifar-10. Technical report, University of Toronto,
Toronto, Canada.
Oliva, A. and Torralba, A. (2006). Building the gist of a
scene: the role of global image features in recognition.
Progress in Brain Research, 14:23–36.
Olshausen, B. and Field, D. (2004). Sparse coding of
sensory inputs. Current Opinion in Neurobiology,
14:481–487.
Pronobis, A. and Caputo, B. (2007). Confidence-base cue
integration for visual place recognition. In IROS 2007.
S. Thrun, W. B. and Fox, D. (2005). Probabilistic Robotics
(Intelligent Robotics and Autonomous Agents). MIT
Press, Cambridge, MA, 1st edition.
Smolensky, P. (1986). Information processing in dynamical
systems foundations of harmony theory. In Rumelhart,
D. and McClelland, J., editors, Parallel Distributed
Processing Explorations in the Microstructure of Cog-
nition, volume 1: Foundations. McGraw-Hill, New
York.
Torralba, A., Fergus, R., and Weiss, Y. (2008). Small codes
and large image databases for recognition. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion - CVPR 08, Anchorage, AK.
Torralba, A., Murphy, K., Freeman, W., and Rubin, M.
(2003). Context-based vision system for place and ob-
ject recognition. Technical Report AI MEMO 2003-
005, MIT, Cambridge, MA.
Ullah, M. M., Pronobis, A., Caputo, B., Jensfelt, P., and
Christensen, H. (2008). Towards robust place recogni-
tion for robot localization. In IEEE International Con-
ference on Robotics and Automation (ICRA’2008),
Pasadena, CA.
Ullah, M. M., Pronobis, A., Caputo, B., Luo, J., and Jens-
felt, P. (2007). The cold database. Technical report,
CAS - Centre for Autonomous Systems. School of
Computer Science and Communication. KTH Royal
Institute of Technology, Stockholm.
Wu, J. and Rehg, J. M. (2011). Centrist: A visual descriptor
for scene categorization. IEEE Trans. Pattern Anal.
Mach. Intell., 33(8):1489–1501.
SemanticPlaceRecognitionbasedonDeepBeliefNetworksandTinyImages
241
