
Timed Trajectory Generation for a Vision-based Autonomous Mobile
Robot in Cluttered Environments
Jorge B. Silva
1
, Cristina P. Santos
1
and Jo˜ao Sequeira
2
1
Industrial Electronic Department, University of Minho, Azur´em, Guimar˜aes, Portugal
2
Industrial Electronic Department, Instituto Superior T´ecnico, Av. Rovisco Pais 1, Lisbon, Portugal
Keywords:
Timed Trajectories, Nonlinear Dynamical System, Extended Kalman Filter, Autonomous Navigation.
Abstract:
An autonomous mobile robot should find feasible trajectories in order to avoid collisions with obstacles in
its environment. This ability to plan collision-free trajectories requires two major aspects: modulation and
generation of trajectories. This is especially important if temporal stabilization of the generated trajectories
is considered. Temporal stabilization means to conform to the planned movement time, in spite of diversified
environmental conditions or perturbations. This timing problem applied for wheeled vehicles has not been
addressed in most current robotic systems. Herein, we extend our previous work by integrating an architecture
able to generate timed trajectories for a wheeled mobile robot, whose goal is to reach a target location within
a specified time, independently of the world complexity.
1 INTRODUCTION
An autonomous mobile robot should find feasible tra-
jectories in order to avoid collisions with obstacles in
its environment. This ability to plan collision-free tra-
jectories requires the combination of generation and
modulation techniques. Moreover, a more relevant is-
sue arises in the path planning problem if temporal
stabilization of the generated trajectories is consid-
ered, in particular when discrete movements are con-
sidered.
Temporal stabilization means to conform to the
planned movement time, in spite of diversified en-
vironmental conditions or perturbations. Controlling
the time of a concrete action requires involving sta-
ble temporal relationships. Moreover, several robotic
tasks have the necessity of temporal stabilization of
actions since they are initiated only once previous ac-
tions have terminated.
To the best of our knowledge, the generation of
timed trajectories embedded in feedback structures
remains an open problem, who has received atten-
tion both in robotics and in neuroscience. Typical
approaches in literature for generating timed con-
trols are based on nonlinear dynamical systems due
to several advantages to address the temporal stabi-
lization problem. Herein, related research concern-
ing to timed trajectories has been verified in several
scopes such as: learning by demonstration, (Ijspeert
et al., 2002), generation of synchronized movement
for biped and quadruped autonomous adaptive loco-
motion (Santos and Matos, 2011), drumming(Ijspeert
et al., 2002), rehabilitation (Ronsse et al., 2010) and
modular robotics (Cui et al., 2010) for instance. The
proposed systems are robust against disturbances but
temporal stabilization is not effectively attempted.
Other works including a dynamical system archi-
tecture (Sch¨oner, 1994) to generate timed trajectories
were implemented in a real vehicle, with a tempo-
ral stabilization mechanism (Santos, 2004). These
works have achieved an online linkage to noisy senso-
rial information by coupling these dynamical systems
to time-varying sensory information. The framework
proposed in (Sch¨oner and Santos, 2001) has suffered
some changes introduced by (Tuma et al., 2009), ar-
guing that the mechanism of temporal stabilization
was not able to preserve the temporal constraint. Ad-
ditionally, they proposed to use the dynamical solu-
tion to control the velocity of the robot.
Later, this challenge of controlling the velocity of
a mobile robot has suffered some novel adaptations
when in (Silva et al., 2010a), it was proposed to ex-
plore the intrinsic properties of the used oscillator.
However, the target was defined geographically and
using vision to detect targets makes the application
more realistic. Thus, in (Silva et al., 2010b) the sen-
sory loop was closed by online acquiring the location
of the target.
431
B. Silva J., P. Santos C. and Sequeira J..
Timed Trajectory Generation for a Vision-based Autonomous Mobile Robot in Cluttered Environments.
DOI: 10.5220/0004031204310434
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 431-434
ISBN: 978-989-8565-22-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
However, when the localization of a target is vi-
sually achieved, there might be situations where the
visual system is unable to detect the target. Then,
in this contribution we extend our previous work to
deal with these localization problems by using an Ex-
tended Kalman Filter (EKF) to estimate the location
of the target. However, the inclusion of an EKF could
affect the temporal nature of architecture. Several
comparative examples of temporal solutions with and
without the EKF are presented to show the intrinsic
robustness of the system.
Additionally, to verify that our proposed architec-
ture can be used in cluttered environments, we vali-
dated it in a hospital environment.
2 SYSTEM OVERVIEW
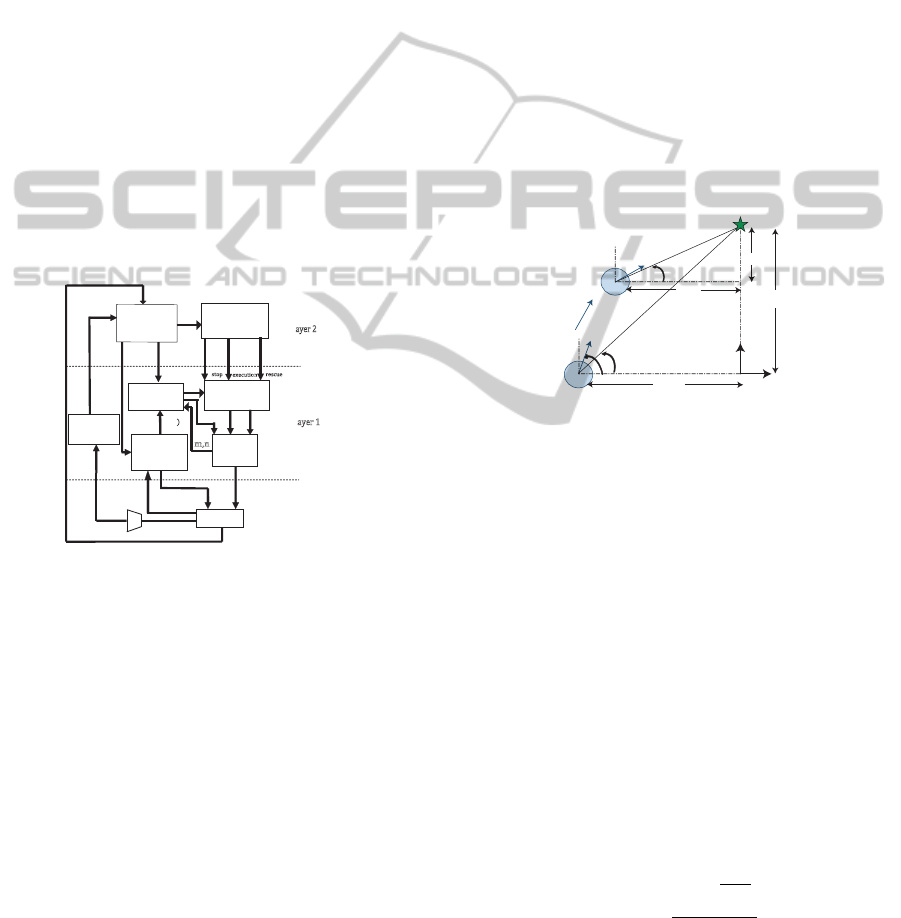
The overall architecture of our system (fig. 1) is hier-
archically divided into two functional layers accord-
ing to their level of abstraction.
Layer 1
(φ )
(
World
µ
Image
Layer 2
Sonars
u
u
execution
rescue
stop
u
h
ψ
tar,
D
D
x
D
y
D
^
^
^
^
ω
A
U O
m
V
V
φ
h
φ
h
φ
m,n
Parameter
Modulation
Velocity
Robot
Behavior
Switching
Heading
Direction
Control
Image
Processing
Timing
Adaptation
Extended
Kalman
Filter
Figure 1: Schematic of the overall architecture.
The second layer is responsible for mimicking the
role of supra-spinal structures in biological systems.
In other words, it selects the most adequate robot mo-
tor behavior according to external conditions and send
them to the first layer at the right timing. Also, an
EKF is used to estimate the localization of the target
relatively to the robot’s position.
The first layer is responsible for controlling the 2D
motion of the robot according to the dynamics of two
behavioral variables: the heading direction φ
h
and the
velocity v. The generated trajectories are modulated
in a simple and straightforward manner through sets
of parameters that are received from the second layer
at the right timing. For a complete explanation please
see (Silva et al., 2010a).
3 EXTENDED KALMAN FILTER
FORMULATION
The EKF operation requires a state space model of the
dynamic system describing the time evolution of the
state to be estimated. Herein, the state to be estimated
is the target position in the robot coordinate system,
which is expressed by the system state discrete vari-
able x
k
= [Dx
k
,Dy
k
,φ
h
k
]
T
.
To calculate the localization of a target relative to
the robot’s position, it is necessary to calculate the
Euclidean distance between the robot and the target
D, as well as the angle from the robot Y-axes to the
target around the robot’s Z-axes ψ
tar
. Both variables
are detailed in fig. 2, in which it is represented the mo-
tion of the robot relative to the target’s position in two
different instants of time. All variables are defined in
the robot coordinate system.
robot
target
Dx
Dy
φ
hk-1
tar
ψ
vk
D
φhk
Dk
Dx
Dyk
k-1
ψ
tar
k
k-1
ωk,
k-1
k
k-1
Y
X
Figure 2: Representation of the variables involved in the
motion of the robot relative to the target. Variables are de-
scribed in the robot coordinate system.
The following relationships may be established
among these variables:
Dx
k
= Dx
k−1
−v
k
cos(φ
h
k
)dt, (1)
Dy
k
= Dy
k−1
−v
k
sin(φ
h
k
)dt, (2)
φ
h
k
= φ
h
k−1
+ ω
k
dt, (3)
where Dx
k
,Dy
k
are respectively the projections onto
the robot X and Y-axes of the distance between the
robot and the target, φ
h
k
is the current heading direc-
tion of the robot, v
k
is the robot forward velocity and
ω
k
is the robot angular velocity. The time step be-
tween two different instants of time is defined by dt
From equations (1),(2) and observing fig. 2 we can
derive the angle ψ
tar
k
that the robot has to follow in
order to reach the target, and the distance D
k
that it
has to travel to reach the target at instant of time k:
ψ
tar
k
= arctan
Dy
k
Dx
k
, (4)
D
k
=
q
Dx
2
k
+ Dy
2
k
. (5)
To estimate our process, we have adopted an EKF
since the next state of the process follows a nonlin-
ear function of the previous state.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
432
4 PERFORMANCE OF
EXTENDED KALMAN FILTER
In order to verify if by adding the EKF to the system
we do not degrade the temporal nature, comparative
examples of the robot moving towards to a target with
and without the EKF are evaluated. Table I shows
the obtained results for several performance indexes
defined in the following.
The robot’s visual system perceives the target as
if it is moving inside an hypothetical circumference,
whose radius is varied in the different experiments,
simulating a noisy target perception.
∆T indicates if the robot satisfied the time con-
straints. It is calculated as the ratio between the time
needed by the robot to reach the target and the speci-
fied movement time. If this value is smaller than 1 the
timing properties are verified.
Table 1: Performance of the system resulting from different
perceptions of the target noise. Averaged over 10 runs for
each noise level.
Radius Version ∆P
f
(m) ∆T E
5 cm non-EKF 0.034 0.970 0.1155
5 cm EKF 0.023 0.957 0.1148
10 cm non-EKF 0.036 0.966 0.1163
10 cm EKF 0.011 0.93 0.1140
20 cm non-EKF 0.039 0.960 0.1166
20 cm EKF 0.007 0.921 0.1104
30 cm non-EKF 0.040 0.957 0.1166
30 cm EKF 0.031 0.939 0.1105
From table I, when the EKF is used the error in
the distance between the final position of the robot
and the target position, ∆P
f
, is smaller. Thus, the in-
clusion of the EKF has reduced the error caused by
the noise perception. We verify that in both modes
(with and without the EKF) ∆T is smaller than 1. This
means that the inclusion of the EKF did not compro-
mise the timing properties.
These results show that the average energy, cal-
culated as E =
√
v
2
+ ω
2
, required for the robot to
successfully complete the missions is lower when the
EKF is used. Also, the inclusion of an EKF does not
destroy the good properties of the architecture pro-
vided that the EKF converges.
5 SIMULATION RESULTS
This simulation demonstrates the reliability of the ar-
chitecture to integrate nonlinear dynamical systems
and an EKF, and simultaneously to preserve the tem-
poral nature of the approach.
At each sensorial cycle, information is acquired,
dynamic equations are calculated and integrated using
an Euler method with a time step of 0.2 s. The robot
is able to reach a maximum velocity of approximately
0.75 m/s.
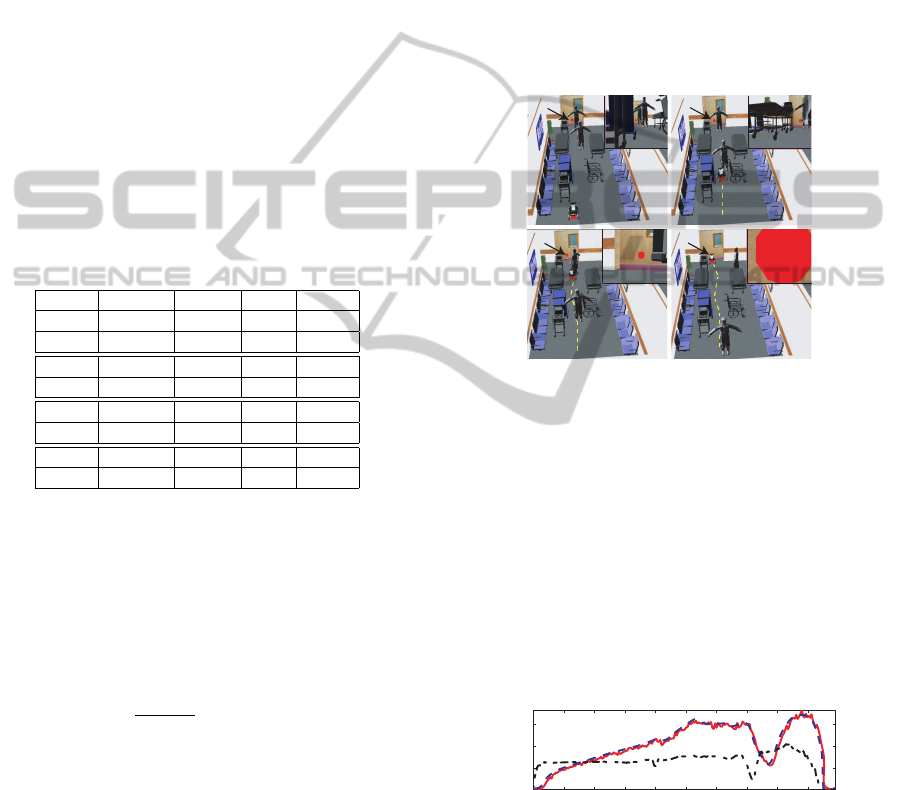
In this simulation the robot has to deal with both
dynamic and static obstacles. Initially, the robot is
stopped and starts moving towards the red mark and
having 20 s to reach it. However, a first person starts
to move in the robot direction obstructing partially its
trajectory, t = 8 s. Another person moves towards the
robot at t = 14 s. The setup for this experiment is de-
picted in fig. 3. In fig. 4 (top)it is depicted the velocity
1
2
3
4
mark
mark
mark
mark
Figure 3: Snapshots of the robot motion.
profile of the robot for this experiment. The amplitude
of the oscillator (black dashed-dotted line) remains
practically constant during the task until the robot has
detected the first person, t = 8 s. At this instant of
time, the amplitude of the oscillator decreases and the
velocity of the robot decreases accordingly. Then, the
velocity of the robot is increased to compensate this
delay. When the second person is detected, a signi-
ficative reduction of the velocity in order to ensure a
safe circumnavigation is required. After the circum-
navigation the velocity of the robot increases to com-
pensate for this provoked delay.
0 2 4 6 8 10 12 14 16 18
0
0.2
0.4
0.6
20
V,m,
A
(m\ )
s
Figure 4: Velocity performed by the robot (continuous red
line), generated velocity by the oscillator (dashed blue line)
and amplitude of the oscillator (black dashed-dotter).
We can verify in fig. 5 that in this experiment, the
robot loses the visual contact with the mark during
several intervals of time, and as expected the EKF fil-
ters the measurements and provides reliable estima-
tions when no measurements are available (shadow
areas).
TimedTrajectoryGenerationforaVision-basedAutonomousMobileRobotinClutteredEnvironments
433

In the bottom panel, we can note that the direction
of the robot,
ˆ
φ
h
, (greencontinuousline) changes when
obstacles in the trajectory are detected (shadow ar-
eas). These changes are required for obstacle circum-
navigation. However, as soon as the obstacles were
circumnavigated, the heading direction converges to
the goal direction
ˆ
ψ
tar
. This experiment demonstrated
0 2 4 6 8 10 12 14 16 18
0
2
4
6
8
20
Dx,Dx
^
(m)
0 2 4 6 8 10 12 14 16 18
-0.5
-0.25
0
0.25
0.5
Dy,Dy
^
(m)
20
0 2 4 6 8 10 12 14 16 18
−0.5
0
0.5
1
1.5
20
Time (s)
^
φ ,
h
ψ
tar
^
(rad)
Figure 5: Top panel (Middle): Measured D
x
(D
y
) by the
robot’s visual system (blue continuous line), and estimated
ˆ
D
x
(
ˆ
D
y
) by the EKF (continuous green line). Bottom: Esti-
mated robot’s heading direction
ˆ
φ
h
(green continuous line),
and the angle
ˆ
ψ
tar
(red dashed line) that the robot has to
follow.
that the EKF is able to filter and to estimate sensorial
information, in this case visual information about the
goal, and simultaneously, to ensure that the temporal
nature of the nonlinear dynamical system approach is
not degraded, even when the robot has to deal with
dynamical obstacles in a cluttered environment.
6 CONCLUSIONS
The purpose of this paper was to address the problem
of generating timed trajectories for an autonomous
mobile robot equipped with noisy and low-level sen-
sory information, while simultaneously has to esti-
mate the goal location using an EKF.
We have successfully demonstrated that the inte-
gration of a standard EKF and a nonlinear dynamical
system to robotics in the same approach without de-
grading the temporal nature of the proposed architec-
ture. Moreover, the inclusion of the EKF has allowed
to reduce the error between the final position of the
robot and the position of the goal.
For future work, we intend to address other more
complex and cluttered environments, as well as to op-
erate in a real hospital environment.
ACKNOWLEDGEMENTS
Work supported by the Portuguese Science Foun-
dation (grant PTDC/EEA-CRO/100655/2008),
and by project FCT PEst-OE/EEI/LA0009/2011.
Jorge B. Silva is supported by PhD Grant
SFRH/BD/68805/2010, granted by the Portuguese
Science Foundation.
REFERENCES
Cui, X., Zhu, Y., Zang, X., Tang, S., and Zhao, J. (2010).
Cpg based locomotion control of pitch-yaw connect-
ing modular self-reconfigurable robots. IEEE Inter-
national Conference on Information and Automation
(ICIA), pages 1410 – 1415.
Ijspeert, A., Nakanishi, J., and Schaal, S. (2002). Learning
attractor landscapes for learning motor primitives. In
Advances in Neural Information Processing Systems
15, pages 1547–1554. MIT Press.
Ronsse, R., Vitiello, N., Lenzi, T., van den Kieboom, J.,
Carrozza, M., and Ijspeert, A. (2010). Human-robot
synchrony:flexible assistance using adaptive oscilla-
tors. IEEE Transactions on Biomedical Enginnering,
58:1001 – 1012.
Santos, C. (2004). Generating timed trajectories for an au-
tonomous vehicle: a non-linear dynamical systems ap-
proach. in Proc. of the IEEE Int. Conf. on Robotics
and Automation (ICRA).
Santos, C. and Matos, V. (2011). Gait transition and mod-
ulation in a quadruped robot: A brainstem-like modu-
lation approach. Robot. Auton. Syst., 59:620 – 634.
Sch¨oner, G. (1994). Dynamic theory of action - perception
patterns: The time before-contact-paradigm. Human
Mov. Science, 3:415 – 439.
Sch¨oner, G. and Santos, C. (2001). Control of movement
time and sequential action through attractor dynamics:
A simulation study demonstrating object interception
and coordination. in Proc. of the 9th Int. Symposium
on Intelligent Robotic Systems (SIRS).
Silva, J., Santos, C., and Matos, V. (2010a). Generating tra-
jectories with temporal constraints for an autonomous
robot. In 8th IEEE International Workshop on Safety,
Security & Rescue, Bremen, Germany, July 26-30.
Silva, J., Santos, C., and Matos, V. (2010b). Timed trajec-
tory generation for a toy-like wheeled robot. In 36th
Annual Conference of the IEEE Industrial Electronics
Society, Glendale, USA, November 07-10, pages 1645
– 1650.
Tuma, M., Iossifidis, I., and Sch¨oner, G. (2009). Temporal
stabilization of discrete movement in variable environ-
ments: an attractor dynamics approach. in IEEE In-
ternational Conference on Robotics and Automation,
Kobe International Conference Center, Kobe, Japan,
pages 863 – 868.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
434
