
Monte Carlo Localization using the Global Appearance of
Omnidirectional Images
Algorithm Optimization to Large Indoor Environments
Lorenzo Fern´andez, Luis Pay´a, David Valiente, Arturo Gil and Oscar Reinoso
Departamento de Ingenier´ıa de Sistemas y Autom´atica
Miguel Hern´andez University, Avda. de la Universidad s/n, Elche (Alicante), Spain
Keywords:
Autonomous Robot, Global Appearance, Panoramic Images, Fourier Signature, Monte-Carlo Localization.
Abstract:
In this paper we deal with the problem of robot localization using the visual information provided by a single
omnidirectional camera mounted on the robot, using techniques based on the global appearance of panoramic
images. Our main objective consists in showing the feasibility of the appearance-based approaches in a lo-
calization task in a relatively large and real environment. First, we study the approaches that permit us to
describe globally the visual information so that it represents with accuracy locations in the environment. Then,
we present the probabilistic approach we have used to compute the most probable pose of the robot when it
performs a trajectory within the map. At the end, we describe the kind of environments and maps we have
used to test our localization algorithms and the final results. The experimental results we show have been
obtained using real indoor omnidirectional images, captured in an office building under real conditions.
1 INTRODUCTION
When a mobile robot has to carry out a task au-
tonomously in an environment, it has to face the prob-
lem of computing its location within a given map with
enough precision so that it can plan the route to follow
to go to the target points during the development of
the task. During the last years, omnidirectional cam-
eras have become a popular tool to carry out these lo-
calization tasks. In this work, we use the information
captured by a single camera that is installed on the
robot. With this system, we capture omnidirectional
images from the environment and we transform these
images into a panoramic format to represent locations
in the environment.
When the appearance-based approach is used,
each scene is represented by a single descriptor which
is computed working with the scene as a whole. For
example, (Menegatti et al., 2004a; Menegatti et al.,
2004b) use a signature based on the Discrete Fourier
Transform of panoramic images to build a visual map
and to perform a probabilistic localization within this
map. (Kr¨ose et al., 2004) use Principal Components
Analysis (PCA) (Kirby, 2001) of panoramic images
for environment modeling and localization. On the
other hand, as no relevant information is extracted, it
is necessary to find a descriptor of the global appear-
ance which optimizes the computational cost of the
localization process. Also, it must work well in large
environments where visual aliasing could be a usual
event.
The main goal of this work consists in evaluating
the feasibility of the appearance-based approaches in
a localization task in a relatively large and real indoor
environmentand studying how the computationalcost
and the accuracy of the results depend on the main
parameters of the descriptor. With this aim, we make
use of the Monte Carlo (MC) Algorithm (Thrun et al.,
2000), which has proved to be robust and efficient in
localization tasks in the field of mobile robotics. We
have decided to describe each omnidirectional image
by a single Fourier descriptor. However, the methods
described here are in fact independent of the descrip-
tor used to represent the images.
2 MONTE-CARLO
LOCALIZATION
In mobile robot localization we are interested in the
estimation of the robot’s pose (location and orienta-
tion, typically, the state x
t
= (x, y, θ)) at time t using a
set of measurements z
1:t
= {z
1
, z
2
, . . . , z
t
} from the en-
439
Fernández L., Payá L., Valiente D., Gil A. and Reinoso O..
Monte Carlo Localization using the Global Appearance of Omnidirectional Images - Algorithm Optimization to Large Indoor Environments.
DOI: 10.5220/0004031904390442
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 439-442
ISBN: 978-989-8565-22-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

vironment and the movements u
1:t
= {u
1
, u
2
, . . . , u
t
}
of the robot (Fox et al., 1999). In Monte Carlo Lo-
calization (MCL) (Thrun et al., 2000), the probability
density function p(x
t
|z
1:t
, u
1:t
) is represented by a set
of M random samples χ
t
= {x
i
t
, i = 1. . . M} extracted
from it, named particles. Each particle can be under-
stood as a hypothesis of the true state of the robot
x
i
t
= (x
i
, y
i
, θ
i
). The weight of each sample (parti-
cle) determines the importance of the particle. The
set of samples defines a discrete probability function
that approximates the continuous belief. The Monte
Carlo Localization algorithm is described briefly in
the next lines, and consists of two phases:
Prediction Phase. At time t a set of particles χ
t
is
generated based on the set of particles χ
t−1
and a
control signal u
t
. This step uses the motion model
p(x
t
|x
t−1
, u
t
). In order to represent this probability
function, the movement u
t
is applied to each particle
while adding a pre-defined quantity of noise. As a re-
sult, the new set of particles χ
t
represents the density
p(x
t
|z
1:t−1
, u
1:t
).
Update Phase. In this second phase, for each particle
in the set χ
t
, the observation z
t
obtained by the robot
is used to compute a weight ω
i
t
. This weight repre-
sents the observation model p(z
t
|x
t
) and is computed
as ω
i
t
= p(z
t
|x
i
t
). The weights are normalized so that
∑
ω
i
t
= 1. As a result, a set of particles accompanied
by a weight χ
t
= {x
i
t
, ω
i
t
} are obtained.
The resulting set χ
t
is calculated by resampling
with replacement from the set χ
t
, where the probabil-
ity of resampling each particle is proportional to its
importance weight ω
i
t
, in accordance with the litera-
ture on the SIR algorithm (Sampling Importance Re-
sampling) (Smith and Gelfand, 1992; Rubin, 1988).
Finally, the distribution p(x
t
|z
1:t
, u
1:t
) is represented
by the set χ
t
.
By means of computing a weight w
i
for each par-
ticle the Monte Carlo algorithm introduces the cur-
rent observation z
t
of the robot. In this case we con-
sider that our map is composed of a set of N bi-
dimensional landmarks L = {l
1
, l
2
, . . . , l
N
} and the po-
sition of these marks on the environment is known.
Each landmark l
j
is represented by an omnidirectional
image I
j
associated and a Fourier Signature descrip-
tor d
j
that describes the global appearance of the om-
nidirectional image (Fernandez et al., 2011), thus
l
j
= {(l
j,x
, l
j,y
), d
j
, I
j
}. d
j
is constructed from the bi-
dimensional Fourier signature with all the elements
arranged in a vector. Using this Fourier descriptor we
compare the descriptor d
t
with the rest of descriptors
d
j
, j = 1. . . N and find the B landmarks in the map
that are closest in appearance with the current image
I
t
. In this sense, we allow the correspondence of the
current observation to several landmarks in the map.
In this work, we propose to compute the weight
of each particle ω
i
t
= p(z
t
|x
i
t
) through a sum of gaus-
sian functionscentered on each landmarkposition and
considering the difference in the descriptors of the
landmarks (images).
ω
i
t
=
B
∑
j=1
exp{−v
j
Σ
−1
l
v
T
j
}exp{−h
j
Σ
−1
d
h
T
j
} (1)
where, v
j
= (l
j,x
, l
j,y
) − (x
i
, y
i
) is the difference
between the position of the landmark l
j
and the posi-
tion (x
i
, y
i
) of the particle i. The matrix Σ
l
is a diago-
nal matrix Σ
l
= diag(σ
2
l
, σ
2
l
). The variance σ
2
l
is cho-
sen experimentally in order to minimize the error in
the localization. h
j
= |d
j
− d
t
| defines the difference
between the module of the Fourier descriptor associ-
ated to the current image observed and the module of
the descriptor associated to the landmark l
j
. The ma-
trix Σ
d
= diag(σ
2
d
) is a k×k matrix, being k the length
of the Fourier descriptor.
3 EXPERIMENTAL RESULTS
In order to acquire the necessary data for the exper-
iments we have used a Pioneer P3-AT mobile robot,
equipped with an omnidirectional camera, and a fixed
platform equipped with an omnidirectional camera
and a laptop. The map was built by carefully ob-
taining omnidirectional images at different positions
on a regular grid in an office-like environment using
the fixed platform. Next, the robot performed some
trajectories within this environment, capturing a new
omnidirectional image and odometry data whenever
it traversed a distance equal to 0.1m. The robot cap-
tured a total of 515 images and traveled around 55m.
The map is composed of a set of 381 images placed
on a grid with a resolution of 0.4m. The map has a
size of 11m in the x axis and 25m in the y axis.
To test the performance of our appearance-based
Monte-Carlo Localization method we have carried
out a series of simulation experiments of robot track-
ing using the sets of images described in the previ-
ous paragraph. We have used an associations num-
ber B equal to 4. We have computed the average er-
ror in the robot position along the trajectory, depend-
ing on the number of Fourier components for differ-
ent number of particles. The average error has been
obtained taking as a reference the real path (ground
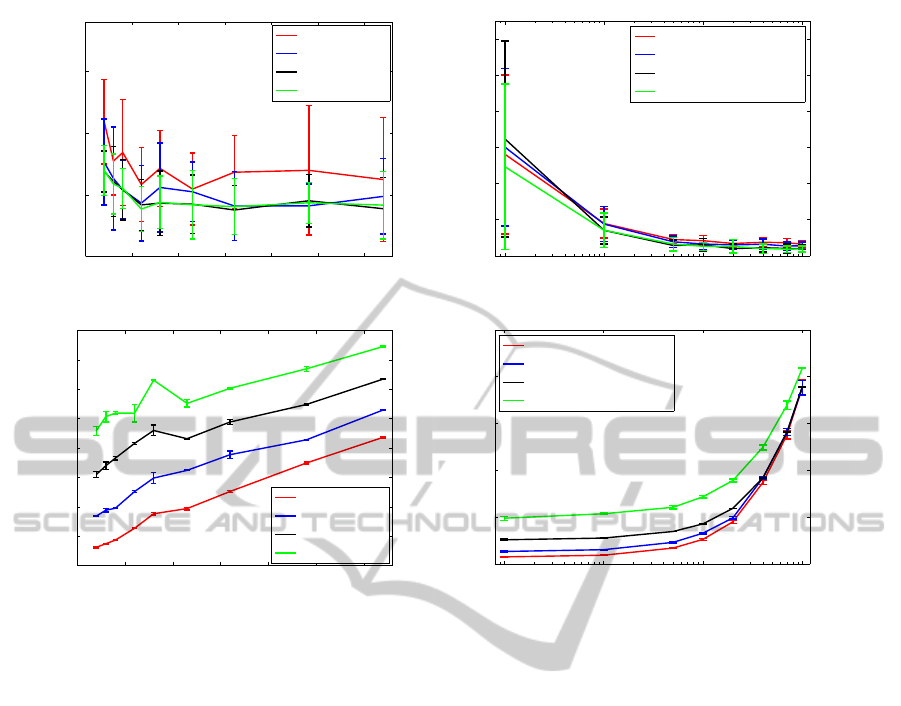
truth) (Figure 1 (a)). We must take into account the
average error of the robot odometry data comparing
with the ground truth is 0.736m. As shown in Figure
1 (a) as we increase the number of Fourier compo-
nents, the localization error along the trajectory tends
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
440
0 20 40 60 80 100 120
0.4
0.45
0.5
0.55
Number of Fourier components
Localization error (m)
500 particles
2000 particles
4000 particles
6000 particles
(a)
10
1
10
2
10
3
10
4
0.4
0.6
0.8
1
1.2
1.4
1.6
log(Number of particles)
Localization error (m)
8 Fourier components
16 Fourier components
32 Fourier components
64 Fourier components
(b)
0 20 40 60 80 100 120
0
50
100
150
200
250
300
350
400
Number of Fourier Components
Time (s)
500 particles
2000 particles
4000 particles
6000 particles
(c)
10
1
10
2
10
3
10
4
0
100
200
300
400
500
log (Number of particles)
Time (s)
8 Fourier components
16 Fourier components
32 Fourier components
64 Fourier components
(d)
Figure 1: (a) Trajectory average error in position versus the number of Fourier components for different number of particles
and (b) trajectory average error in position versus the number of particles for different number of Fourier components, with
respect to the real path, (c) computation time needed to complete the estimation of the trajectory of the robot versus the
number of Fourier components for different number of particles and (d) versus the number of particles for different number
of Fourier components.
to decrease, but a threshold number of components
appears and when we increase this number, the er-
ror does not decrease significantly (this threshold is
around 24 Fourier Components for a relatively high
number of particles). We can also see that the graph
tendency is quite similar for the four different number
of particles tested.
To compare the performance of our method with
respect to the number of particles we have carried out
a set of experiments of robot tracking in which we
have tested the trajectory average error in the position
of the robot depending of this number of particles.
Figure 1 (b) shows how the increase of the number
of particles makes the error with respect the real path
to decrease until a certain value from which the error
remains small (about 2000 particles). We arrive to the
same conclusion as in the previous experiment.
Figure 1 (c) shows the average time needed to
carry out the complete Monte-Carlo localization ex-
periment with respect to the number of Fourier com-
ponents and for different number of particles. On the
other hand, Figure 1 (d) show the dependence of the
computation time with respect to the number of parti-
cles.
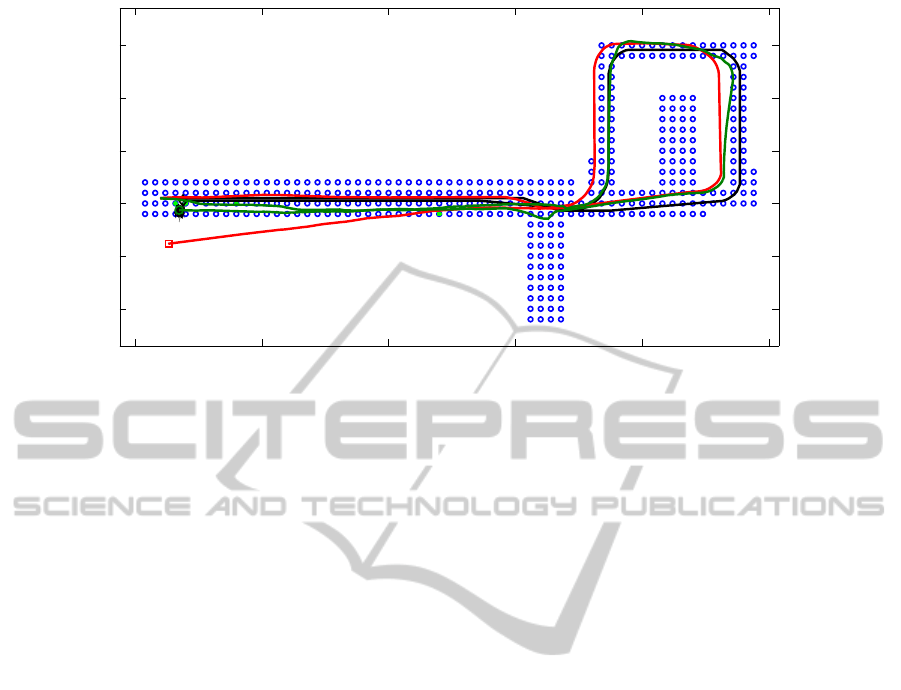
Figure 2 presents an example of a relatively accu-
rate case of robot tracking using 4000 particles and
32 Fourier components. In this figure, the position of
the map images is indicated with a blue circle, the po-
sition of the associated landmarks is indicated with a
green solid circle (four associations are used, as stated
before), the real path is represented by a black line,
the robot odometry path is presented by a red line, the
path obtained with our method is shown as a green
line and finally, the particles are represented as black
dots. As we can observe, our algorithm is able to cope
with robot turnings and the trajectory estimated is ac-
curate enough for many robot applications in indoor
environments.
4 CONCLUSIONS
In this paper we have tested the performance of a
Monte-Carlo localization technique using the global
MonteCarloLocalizationusingtheGlobalAppearanceofOmnidirectionalImages-AlgorithmOptimizationtoLarge
IndoorEnvironments
441
8
10
12
14
16
18
0 5 10 15 20 25
Y (m)
X (m)
(a)
Figure 2: An experiment of Monte-Carlo localization using 4000 particles and 32 Fourier components.
appearance of panoramic images. We compare our
results with the real trajectory in an large indoor en-
vironment. We have built the appearance-based de-
scriptor using the Fourier signature of panoramic im-
ages. We have evaluated the performance of the
method in the case of a local localization. Our sys-
tem is able to track the position of the robot while
moving if we tune correctly the parameters involved
in the process. We have proved that the precision of
our method varies with the number of particles used
and the number of Fourier components. Furthermore,
as we increase the number of particles in the system,
the average error of localization decreases rapidly un-
til a certain point from which the error remains small
with no appreciable improvement. Finally, as we in-
crease the number of Fourier components, the local-
ization error decreases, but from a number of compo-
nents the error does not decrease significantly. These
experiments show the feasibility of using appearance-
based techniques in robot localization, maintaining a
reasonable computational cost, so, the navigation can
be carried out in real time.
ACKNOWLEDGEMENTS
This work has been supported by the Spanish govern-
ment through the project DPI2010-15308. ”Explo-
raci´on Integrada de Entornos Mediante Robots Co-
operativos para la Creaci´on de Mapas 3D Visuales y
Topol´ogicos que Puedan ser Usados en Navegaci´on
con 6 Grados de Libertad”.
REFERENCES
Fernandez, L., Paya, L., Reinoso, O., and Amoros, F.
(2011). Appearance-based visual odometry with om-
nidirectional images. a practical application to topo-
logical mapping. In Proc. of ICINCO, pages 205–210.
Fox, D., Burgard, W., and Thrun, S. (1999). Markov lo-
calization for mobile robots in dynamic environments.
JAIR, 11:391–427.
Kirby, M. (2001). Geometric data analysis. Wiley Inter-
science.
Kr¨ose, B., Bunschoten, R., Hagen, S. T., Terwijn, B., and
Vlassis, N. (2004). Environment modeling and local-
ization from an omnidirectional vision system. IEEE
Robotics and Automation Magazine.
Menegatti, E., Maeda, T., and Ishiguro, H. (2004a). Image-
based memory for robot navigation using properties
of omnidirectional images. Robotics and Autonomous
Systems, 47(4):251–276.
Menegatti, E., Zocaratto, M., Pagello, E., and Ishiguro, H.
(2004b). Image-based monte carlo localisation with
omnidirectional images. Robotics and Autonomous
Systems, 48(1):17–30.
Rubin, D. B. (1988). Bayesian statistics 3. Oxford Univer-
sity Press.
Smith, A. F. M. and Gelfand, A. E. (1992). Bayesian statis-
tics without tears: a sampling-resampling perspective.
American Statistician, 46(2):84–88.
Thrun, S., Fox, D., Burgard, W., and Dellaert, F. (2000).
Robust monte carlo localization for mobile robots. Ar-
tificial Intelligence, 128(1-2):99–141.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
442
