
Performance Shaping through Cost Cumulants and Neural
Networks-based Series Expansion
Bei Kang, Chukwuemeka Aduba and Chang-Hee Won
Department of Electrical and Computer Engineering, Temple University, Philadelphia, PA 19122, U.S.A.
Keywords:
Statistical Optimal Control, Cumulant Minimization, Neural Networks, Cost Cumulants, Performance
Shaping.
Abstract:
The performance shaping method is addressed as a statistical optimal control problem. In statistical control,
we shape the distribution of the cost function by minimizing n-th order cost cumulants. The n-th cost cumu-
lant, Hamilton-Jacobi-Bellman (HJB) equation is derived as the necessary condition for the optimality. The
proposed method provides an approach to control a higher order cost cumulant for stochastic systems, and
generalizes the traditional linear-quadratic-Gaussian and Risk-Sensitive control methods. This allows the cost
performance shaping via the cost cumulants. Moreover, the solution of general n-th cost cumulant control is
provided by numerically solving the HJB equations using neural network method. The results of this paper
are demonstrated through a satellite attitude control example.
1 INTRODUCTION
We shape the performance of the system through the
statistical properties of the cost function. In linear-
quadratic-Gaussian (LQG) control, the performance
is optimized by minimizing the mean of the cost func-
tion (Fleming and Rishel, 1975). In statistical opti-
mal control, we minimize any cost cumulant to im-
prove the performance of the system. So far the first
mean (LQG) and denumerable sum of all the cumu-
lants (risk-sensitive) of the cost function are inves-
tigated (Lim and Zhou, 2001). However, there are
other statistical parameters that we can vary to shape
the performance. This is achieved by minimizing n-th
cost cumulants. The study of cost control cumulant
was initiated by (Sain, 1966). The authors extended
the theory of cost cumulant control to third and fourth
cumulants for a nonlinear system with nonquadratic
cost and derived the corresponding HJB equations
(Won et al., 2010). HJB equation was derive, but
the solution was not determined. In fact, most HJB
equations do not have analytical solutions except for
the special cases of linear systems with quadratic cost
functions. Thus, numerical approximate methods are
needed to solve HJB equation. For the first two cu-
mulant case, we solved the HJB equation using neu-
ral networks in (Kang and Won, 2010). In this paper,
we extend this result to n-th cumulants. This is not a
simple extension of the results in (Won et al., 2010).
There, we developed a procedure to solve higher or-
der cost cumulant problem using the results of the mo-
ments. In this paper, we use induction to derive n-th
cumulant HJB equation, which was not a trivial task.
This n-th cumulant HJB equation corresponds to the
performance shaping idea. Then we solve this HJB
equation using a neural network method.
A power series expansion to approximate the
value function for an infinite-time horizon determin-
istic system was given in (Alberkht, 1961). Apply-
ing Galerkin approximate method to solve the gen-
eralized Hamilton-Jacobi-Bellman (GHJB) was given
in (Beard et al., 1997). (Chen et al., 2007) proposed
using neural network methods to solve the optimal
control problem of a nonlinear finite time system. If
we define the weighting and the basis functions as
polynomials, the neural network is in fact equivalent
to power series expansion in that we use coefficients
of the power expansion as the weights in neural net-
works. However, neural network method has the po-
tential to be more than simple power series expansion
by adding additional layers of neurons. In this work,
we extend the system dynamics of (Chen et al., 2007)
to stochastic systems. Then we solve the HJB equa-
tions for the n-th cost cumulant control problem using
neural network approximation method.
Section 2 states the problem and defines the nota-
tions used in this paper. Section 3 develops the HJB
equations for the n-th cost cumulant control of the
196
Kang B., Aduba C. and Won C..
Performance Shaping through Cost Cumulants and Neural Networks-based Series Expansion.
DOI: 10.5220/0004032101960201
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 196-201
ISBN: 978-989-8565-21-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

system. The induction is utilized in the derivation. In
order to solve the statistical optimal control problem,
we use neural network approximations for HJB equa-
tions in Section 4. The simulation results for the satel-
lite attitude control application is presented in Section
5. Finally conclusions are given in the last section.
2 PROBLEM FORMULATION
Consider a stochastic differential equation:
dx(t) = f(t, x(t), u(t))dt + σ(t, x(t))dw(t),
(1)
where t ∈ [t
0
,t
F
], x(t
0
) = x
0
, x(t) ∈ R
n
, u(t) ∈U ⊂ R
m
,
and dw(t) is a Gaussian random process of dimension
d with zero mean and covariance of W(t)dt. The sys-
tem control is given as
u(t) = k(t, x(t)),t ∈ T.
(2)
The system cost function is given as:
J(t, x(t);k) = ψ(x(t
F
))
+
Z
t
F
t
l(s, x(s)) + k
′
(s, x(s))Rk(s, x(s))
ds,
(3)
where ψ(x(t
F
)) is the terminal cost, l(s, x(s)) is a pos-
itive definite function, R is the positive definite matrix.
The goal is to find an optimal controller for system (1)
which minimizes the n-th cumulant of the cost func-
tion (3), such that V
n
(t, x, k(t, x)) = min
k∈K
M
{V
n
(t, x, k)}.
We now introduce a backward evolution operator
O (k), defined by
O (k) =
∂
∂t
+
n
∑
i=0
f
i
(t, x, k(t, x))
∂
∂x
i
+
n
∑
i, j=1
σ(t, x)W(t)σ
′
(t, x)
i, j
∂
2
∂x
i
∂x
j
.
Then the n-th cumulant of cost function, we in-
troduce the n-th moments of cost function which is
defined as:
M
i
(t, x, k(t, x)) = E
n
J
i
(t, x, k(t, x))
x(t) = x
o
Next, we introduce some definitions,
Definition 2.1. A function M
j
: Q
0
→ R
+
is an
admissible j-th moment cost function if there ex-
ists an admissible control law k such that M
j
(t, x) =
E
tx
J
i
(t, x, k(t, x))
for t ∈ T, x ∈ R
n
.
Definition 2.2. The admissible moment cost func-
tions M
1
, ..., M
j
defines a class of control laws K
M
such that for each k ∈ K
M
, M
1
, ..., M
j
satisfy Defini-
tion 2.1.
Definition 2.3. A function V
j
: Q
0
→ R
+
is an admis-
sible j-th cumulant cost function if there exists an ad-
missible control laws k such that V
j
(t, x) = V
j
(t, x, k).
Now, we mathematically formulate the statistical
optimal control problem as follows. Under the as-
sumption that M
1
, ..., M
n−1
exist and are admissi-
ble, we find an optimal control k
∗
∈ K
M
such that
V
∗
n
(t, x) = V
n
(t, x, k
∗
) satisfies V
∗
n
(t, x) ≤ V
n
(t, x, k) for
all k(t, x) ∈ K
M
(t, x).
The n-th cumulant of the cost function is given by
the following recursion formula (Smith, 1995), where
we suppress the arguments for the sake of brevity.
V
n
= M
n
−
n−2
∑
i=0
(n− 1)!
i!(n− 1− i)!
M
n−1−i
V
i+1
.
(4)
It is shown in (4) that the n-th order cumulant
can be calculated from the n-th order moment and the
lower order moments and cumulants. In the next sec-
tion, the above definitions and formulas will be used
to derive the HJB equations for the n-th order cumu-
lant minimization.
3 n-th CUMULANT HJB EQ.
Before we derive the n-th cumulant HJB equation,
we introduce the n-th moment HJB equation. (Sain,
1967) derived the n-th moment HJB equation given in
recursive form,
O (k)[M
n
(t, x, k)] + nM
n−1
(t, x, k)L(t, x, k) = 0
(5)
Using (5) and the Definition 2.1, we have the fol-
lowing theorem which gives the necessary condition
for the optimality. Consider on open set Q
0
⊂ (
¯
Q
0
).
Theorem 3.1. Let M
j
(t, x) ∈ C
1,2
p
(Q
0
)∩C(
¯
Q
0
) be the
j-th admissible moment cost function, assume the ex-
istence of an optimal controller k
∗
∈ K
M
such that
M
∗
j
(t, x) = M
j
(t, x, k
∗
) = min
k∈K
M
M
j
(t, x, k)
,
then k
∗
and M
∗
j
satisfy the following HJB equation,
O (k)
M
∗
j
(t, x)
+ jM
j−1
(t, x)L(t, x, k
∗
) = 0,
(6)
for t ∈ T, x ∈ R
n
and the terminal condition is given
as M
∗
j
(t
f
, x) = ψ(x(t
f
)).
Proof: See (Won et al., 2010).
The following Lemmas are used to obtain the n-th
cumulant HJB equation.
Lemma 3.1. Consider two functions M
i
(t, x), V
j
(t, x)
∈ C
1,2
p
(Q) ∩C(
¯
Q), where i and j are non-negative in-
tegers, then
O (k)[M
i
(t, x)V
j
(t, x)]
= O (k)[M
i
(t, x)]V
j
(t, x) + M
i
(t, x)O (k)[V
j
(t, x)]
+
∂M
i
(t, x)
∂x
′
σ(t, x)Wσ(t, x)
′
∂V
j
(t, x)
∂x
.
PerformanceShapingthroughCostCumulantsandNeuralNetworks-basedSeriesExpansion
197

Lemma 3.2. Let V
i
(t, x), ..., V
k−1
(t, x) ∈ C
1,2
p
(Q) ∩
C(
¯
Q) be admissible cost cumulant functions, then
1
2
k−1
∑
s=1
k!
s!(k− s)!
∂V
s
∂x
′
σWσ
′
∂V
k−s
∂x
=
k−2
∑
i=0
(k− 1)!
i!(k− 1− i)!
∂V
k−1−i
∂x
′
σWσ
′
∂V
i+1
∂x
.
Proof: Omitted for brevity.
The main result of this paper is given in the fol-
lowing theorem. We use induction to prove the gen-
eral n-th cumulant optimal control.
Theorem 3.2. (n-th cumulant HJB equation) Let
V
1
(t, x),V
2
(t, x), . . . ,V
n−1
(t, x) ∈ C
1,2
p
(Q
0
) ∩C(
¯
Q
0
) be
an admissible cumulant cost function for the con-
trol. Assume the existence of an optimal control law
k
∗
V
k
|M
∈ K
M
and an optimal value function V
∗
n
(t, x) ∈
C
1,2
p
(Q
0
) ∩ C(
¯
Q
0
). Then the minimal n-th cumu-
lant cost function V
∗
n
(t, x) satisfies the following HJB
equation,
0 = min
k∈K
M
(
O (k)[V
∗
n
]
+
1
2
n−1
∑
s=1
n!
s!(n− s)!
∂V
s
∂x
′
σWσ
′
∂V
n−s
∂x
)
,
(7)
for (t, x) ∈
¯
Q
0
, with the terminal conditionV
∗
n
(t
f
, x) =
0.
Proof: The mathematical induction method is used
here to prove the theorem. We proved that when n=2,
the second cost cumulant HJB equation satisfies (1).
The third and fourth cumulant cases were proved in
(Won et al., 2010). Thus, we assume that this theorem
holds for the second, third and (n-1)-th cumulant case.
We will show that the theorem also holds for the n-th
cumulant case. Henceforth, the arguments of M and
V are suppressed for brevity.
Let V
∗
n
be in the class of C
1,2
p
(Q) ∩ C(
¯
Q). Apply
the backward evolution operator O (k) to the recursive
formula (4), we have
0 = O (k)[V
∗
n
] − O (k)[M
n
]
+
n−2
∑
i=0
(n− 1)!
i!(n− 1− i)!
O (k)[M
n−1−i
V
i+1
].
(8)
From Theorem 3.1, we have
O (k)[M
n
] + nM
n−1
L = 0.
(9)
Then, from Lemma 3.1, and letting i = n − 1− i, j=
i+ 1, we obtain
O (k)[M
n−1−i
V
i+1
] = O (k)[M
n−1−i
]V
i+1
+ M
n−1−i
O (k)[V
i+1
] +
∂M
n−1−i
∂x
′
σWσ
′
∂V
i+1
∂x
.
(10)
Substitute (9), (10) into (8), and we have
0 = O (k)[V
∗
n
] + nM
n−1
L
+
n−2
∑
i=0
(n− 1)!
i!(n− 1− i)!
"
O (k)[M
n−1−i
]V
i+1
+ M
n−1−i
O (k)[V
i+1
] +
∂M
n−1−i
∂x
′
σWσ
′
∂V
i+1
∂x
#
.
(11)
Use (9) again for O (k)[M
n−1−i
] in (11) results in
0 = O (k)[V
∗
n
] + nM
n−1
L
+
n−2
∑
i=0
(n− 1)!
i!(n− 1− i)!
"
− (n− 1− i)M
n−2−i
V
i+1
L
+ M
n−1−i
O (k) [V
i+1
] +
∂M
n−1−i
∂x
′
σWσ
′
∂V
i+1
∂x
#
.
(12)
Using the formula in (Stuart and Ord, 1987),
∂M
i
∂V
j
=
i!
j!(i− j)!
M
i− j
,
then
∂M
n−1−i
∂x
=
n−1−i
∑
j=1
(n− 1− i)!
j!(n− 1− i− j)!
M
n−1−i− j
∂V
j
∂x
.
Thus, using the assumption that the theorem holds,
from second order to (n− 1)-th order cumulant case,
(12) becomes
0 = O (k)[V
∗
n
] −
n−2
∑
i=1
(n− 1)!
i!(n− 1− i)!
"
M
n−1−i
i−1
∑
j=0
i!
j!(i− j)!
∂V
i− j
∂x
′
σWσ
′
∂V
j+1
∂x
#
+
n−2
∑
i=0
(n− 1)!
i!(n− 1− i)!
"
n−1−i
∑
j=1
(n− 1− i)!
j!(n− 1− i− j)!
M
n−1−i− j
∂V
j
∂x
′
σWσ
′
∂V
i+1
∂x
#
.
(13)
From (13), we notice that both the second and third
term on the right hand side contain the moment from
{M
x
}, where x = 1, 2, .. . , n − 2. Therefore, it is
feasible to combine two summations with respect to
M
x
and simplify the equation. For derivation conve-
nience, we use p and q instead of i and j within the
bracket of the second term of (13),
M
n−1−i
i−1
∑
j=0
i!
j!(i− j)!
∂V
i− j
∂x
′
σWσ
′
∂V
j+1
∂x
,
to distinguish the notations of the second and third
term in (13). Note that the notations p, q and i, j are
indeed equivalent. Therefore, (13) is rewritten as
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
198

O (k)[V
∗
n
] −
n−2
∑
p=1
(n− 1)!
p!(n− 1− p)!
"
M
n−1−p
p−1
∑
q=0
p!
q!(p− q)!
∂V
p−q
∂x
′
σWσ
′
∂V
q+1
∂x
#
+
n−2
∑
i=0
(n− 1)!
i!(n− 1− i)!
"
n−2−i
∑
j=1
(n− 1− i)!
j!(n− 1− i− j)!
M
n−1−i− j
∂V
j
∂x
′
σWσ
′
∂V
i+1
∂x
#
+
n−2
∑
i=0
(n− 1)!
i!(n− 1− i)!
"
∂V
n−1−i
∂x
′
σWσ
′
∂V
i+1
∂x
#
= 0.
(14)
Now, let us focus on the second and third terms of
(14). We consider the second and third terms as func-
tions with respect to M
x
. We will compare the coef-
ficients of the same M
x
on second and third terms,
i.e when M
n−1−p
= M
n−1−i− j
. When k − 1 − p =
k− 1− i− j, then p = i+ j, then we will determine the
corresponding coefficients associated with M
n−1−p
=
M
n−1−i− j
via the following procedure. In the second
term of (14), the coefficient associated with M
n−1−p
is
−
p−1
∑
q=0
(n− 1)!
q!(n− 1− p)!(p − q)!
"
∂V
p−q
∂x
′
σWσ
′
∂V
q+1
∂x
M
n−1−p
#
.
(15)
For the third term in (14) because p = i+j, then for
each p in [1, n-2], there are combinations of i and j,
such that the summation of which are equal to p such
as p=0+p, p=1+(p-1), ...and p=(p-1)+1. Because
the range for index i is i = 0, 1, 2, ..., p-1, when we
look for the coefficient of M
n−1−i− j
when M
n−1−i− j
=
M
n−1−p
, we must find summation of the coefficient of
M
n−1−i− j
for all combinations of i and j. Therefore,
the corresponding coefficient is
i=p−1
∑
i=0, j=p=i
C
M
n−1−i− j
,
where C
M
n−1−i− j
is the coefficient for each i and j
which lead to the same k-1-i-j. Substitute p = i +
j, i = 0, 1, 2, ..., p-1, j = p-i back to the third term of
(14), then the coefficient associated with M
n−1−i− j
is
p−1
∑
i=0
(n− 1)!M
n−1−p
i!(n− 1− i)!
"
(n− 1− i)!
(p− i)!(n − 1 − p)!
∂V
p−i
∂x
′
σWσ
′
∂V
i+1
∂x
#
=
p−1
∑
i=0
(n− 1)!
i!(n− 1− p)!(p − i)!
"
∂V
p−i
∂x
′
σWσ
′
∂V
i+1
∂x
M
n−1−p
#
.
(16)
Compare (15) and (16), we notice that since p is
equivalent to i and q is equivalent to j, it is obvi-
ous that they have exactly format except for the signs.
Thus they will cancel with each other when they are
summed up. Therefore, the summation of the sec-
ond and third term on (14) will be zero. Then we
apply Theorem 3.1, (14) becomes (7). The theorem is
proved.
4 NEURAL NETWORK APPROX.
Neural network method based on series expansion ap-
proximate concept for HJB equations is applied to
solve the value function of the HJB equations gen-
erated in the Section 3.
In our neural network approach, several neural
network input function are multiplied by their cor-
responding weights and then summed up to pro-
duce output which is the approximated value func-
tion. In this paper, polynomial series expansion
¯
δ
L
(x) = {δ
1
(x), δ
2
(x), . . . , δ
L
(x)}
′
is the neural net-
work input function while the weights of the series ex-
pansion is w
L
(t) = {w
1
(t), w
2
(t), . . . , w
L
(t)}
′
. These
weights are time-dependent. The n-th cumulant value
function is represented as V
∗
nL
(x,t) = w
′
L
(t)
¯
δ
L
(x) =
∑
L
i=1
w
′
i
(t)δ
i
(x). The subscript L in the value func-
tion represents the order of the polynomial series. The
higher the order of the series, the closer the approxi-
mate value gets to the real value.
In Theorem 3.2, the HJB equation for the n-th
cumulant case is given. We need to solve this HJB
equation to find the optimal controller. The optimal
controller k
∗
for the n-th cumulant case has the form.
k
∗
= −
1
2
R
−1
B
′
∂V
1
∂x
+ γ
2
∂V
2
∂x
. . . + γ
n
∂V
∗
n
∂x
,
(17)
with terminal condition V
∗
n
(t
f
, x) = 0 where
γ
2
, γ
3
, . . . , γ
n
are the Lagrange multipliers. From
(1), we assume that
f(t, x(t), k(t, x(t))) = g(t, x) + B(t, x)k(t, x),
where the matrices R(t) > 0, B(t, x) are continuous
real matrices. We substitute k
∗
back into the HJB
equation from the first to n-th cumulant cases, then
use neural network series expansion to approximate
each HJB equation. Assuming terminal conditions for
the value function V
1
,V
2
, . . . ,V
n
are zero.
PerformanceShapingthroughCostCumulantsandNeuralNetworks-basedSeriesExpansion
199

Then the neural network approximations are used.
We approximage V
1
by V
1L
(x,t) = w
′
1L
(t)
¯
δ
L
(x), V
2
by V
2L
(x,t) = w
′
2L
(t)
¯
δ
L
(x), etc. We obtain differen-
tial equations for the weigths. The n-th order one is
given as an example.
˙
w
nL
(t) =
− h
¯
δ
nL
(x),
¯
δ
nL
(x)i
−1
Ω
h∇
¯
δ
nL
(x)g(x),
¯
δ
nL
(x)i
Ω
¯w
nL
(t)
+
1
2
h
¯
δ
nL
(x),
¯
δ
nL
(x)i
−1
Ω
A
L
¯w
nL
(t)
+
n
∑
i=2
γ
2
i
2
h
¯
δ
nL
(x),
¯
δ
nL
(x)i
−1
Ω
B
iL
¯w
nL
(t)
−
1
2
n−1
∑
i=1
n!
i!(n− i)!
h
¯
δ
nL
(x),
¯
δ
nL
(x)i
−1
Ω
F
iL
¯w
(n−i)L
−
1
2
h
¯
δ
nL
(x),
¯
δ
nL
(x)i
−1
Ω
G
L
¯w
nL
.
(18)
The terminal conditions ¯w
1L
(t
f
),..., ¯w
nL
(t
f
) are
assumed zero and the quantities A
L
, B
iL
, C
L
, F
iL
and
G
L
are defined as follows,
A
L
=
L
∑
s=1
w
1s
(t)h∇
¯
δ
1L
(x)BR
−1
B
′
∇
¯
δ
1s
(x)
¯
δ
1L
(x)i
Ω
,
B
iL
=
L
∑
s=1
w
is
(t)h∇
¯
δ
iL
(x)BR
−1
B
′
∇
¯
δ
is
(x)
¯
δ
1L
(x)i
Ω
,
C
L
= htr
σWσ
′
∇
∇
¯
δ
′
1L
(x) ¯w
1L
(t)
,
¯
δ
1L
(x)i
Ω
,
F
iL
=
L
∑
s=1
w
is
(t)h∇
¯
δ
(n−i)L
(x)σWσ
′
∇
¯
δ
is
(x)
¯
δ
nL
(x)i
Ω
,
G
L
= htr
σWσ
′
∇
∇
¯
δ
′
nL
(x) ¯w
nL
(t)
,
¯
δ
nL
(x)i
Ω
.
To solve the n-th cumulant neural network equation,
we need to simultaneously solve all the n-th cumulant
equation by converting the PDEs to neural network
ODEs. Then, we solve the approximated ODEs with
the corresponding Lagrange multipliers γ
2
, γ
3
, γ
4
to
γ
n
.
5 SIMULATION
In this section, we will use the neural network to cal-
culate the first, second third and fourth cumulant opti-
mal control for a satellite attitude control application
studied in (Won, 1999). This is a linear system with
quadratic cost function. We define the state variables
as follows: ¯x = [x
1
, x
2
, x
3
, x
4
, x
5
, x
6
, x
7
, x
8
, x
9
, x
10
] =
[φ, θ, ψ, ω
x
, ω
y
, ω
z
, Ω
1
, Ω
2
, Ω
3
, Ω
4
]. φ, ψ and θ are
the roll, yaw and pitch Euler angles of the satellite.
ω
x
, ω
y
and ω
z
are the angular velocities of the satel-
lite. Ω
1
, Ω
2
, Ω
3
and Ω
4
are the reaction wheel ve-
locities. We consider the fourth cumulant control
and analyze the system state space form and derive
the HJB equations for the fourth cumulant control.
Let V
1L
(x,t) = w
′
1L
(t)
¯
δ
L
(x) to approximate V
1
(x,t),
V
2L
(x,t) = w
′
2L
(t)
¯
δ
L
(x) to approximate V
2
(x,t), etc.
The basis function
¯
δ
L
(x) is chosen from the expan-
sion of a polynomial generating function (x
1
+ x
2
+
x
3
+ x
4
+ x
5
+ x
6
+ x
7
+ x
8
+ x
9
+ x
a
)
2
which contains
55 elements. Thus, the weights to be determined
are defined as w
1L
(t) = {w
1
, w
2
, . . . , w
55
}, w
2L
(t) =
{w
56
, w
57
, . . . , w
110
}, w
3L
(t) = {w
111
, w
112
, . . . , w
165
},
w
4L
(t) = {w
166
, w
167
, . . . , w
220
}. Using neural net-
work method, we solve for the approximatedV
1L
(x,t),
V
2L
(x,t), V
3L
(x,t) and V
4L
(x,t) .
Here we simulate the first four cost cumulant con-
trol, i.e n = 4. Because we use Lagrange multiplier
method to derive the second, third and fourth cost cu-
mulant HJB equations, we solve the HJB equations
by assigning different values for the Lagrange multi-
pliers γ
2
, γ
3
and γ
4
. In all simulation, we fix γ
2
= γ
3
= 0.001, while γ
4
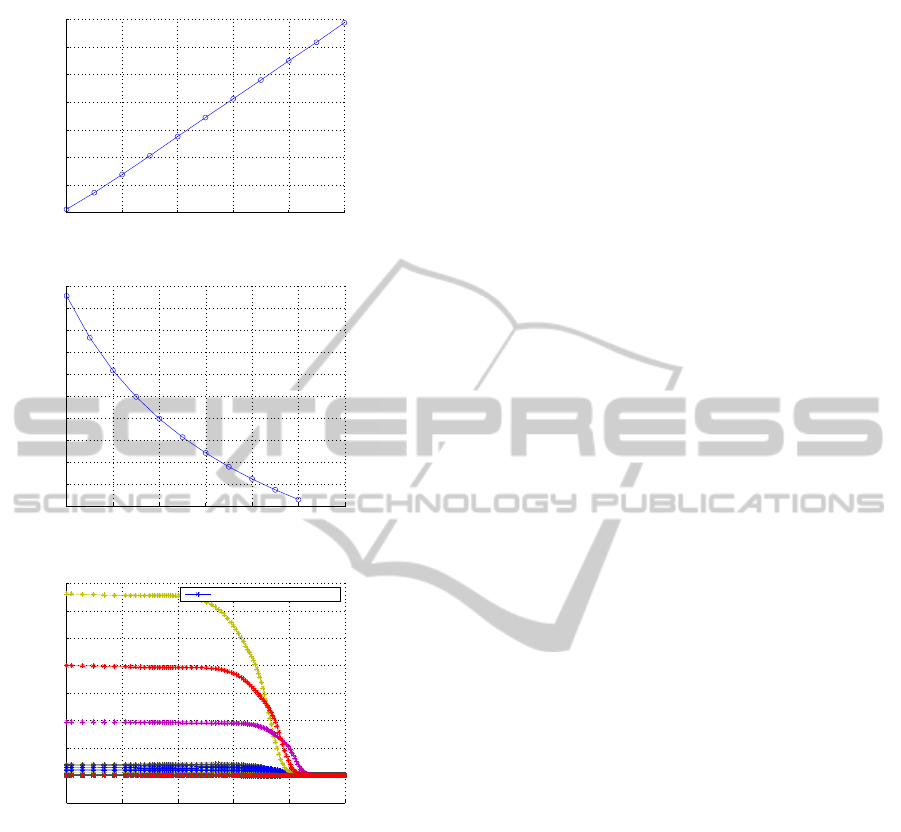
vary from 0 to 0.0001. In Fig. 1(a),
we observe that first cumulant V
1
increases with in-
creases in γ
4
and the smallest V
1
is obtained when γ
4
is 0. For brevity we did not show second and third cu-
mulant value functions as a function of gamma
4
. The
second cumulant V
2
decreases with with increases in
γ
4
and reaches a minimum when γ
4
= 0.0001. This is
related to the variance of the cost function. It is ob-
served thatV
3
decreases with increases in γ
4
. Fig. 1(b)
shows the fourth cumulant V
4
as γ
4
varies in value. It
is observed V
4
decreases with increases in γ
4
. Fig.
1(c) shows that the neural network weights converge
to constants when integrated backward in time.
Depending on the desired statistical properties of
the cost function, the engineer will choose the appro-
priate Lagrange multiplier values. In the satellite at-
titude control case, the mean and the variance are the
important factors. Thus γ
4
equal to 0.0001 is a good
choice. From the value functions, the corresponding
optimal controller k
∗
is determined by substituting V
1
,
V
2
, V
3
and V
4
back to the following equation,
k
∗
= −
1
2
R
−1
B
′
∂V
1
∂x
+ γ
2
∂V
2
∂x
+ γ
3
∂V
3
∂x
+ γ
4
∂V
∗
4
∂x
.
(19)
The optimal controller k
∗
(t,x) is the minimal
fourth cumulant controller. Similarly, the minimal
first cumulant controller (LQG control) is found by
letting γ
2
= γ
3
= γ
4
= 0. Following similar approach,
we can determine higher order cumulant optimal con-
troller.
6 CONCLUSIONS
In this paper, we studied the statistical optimal control
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
200
0 0.2 0.4 0.6 0.8 1
x 10
−4
9600
9700
9800
9900
10000
10100
10200
10300
First Cumulant, γ
4
from 0 to 0.0001, γ
2
= γ
3
= 0.001
γ
4
V
1
−Cost Cumulant Value Function
(a) V1
0 0.2 0.4 0.6 0.8 1 1.2
x 10
−4
2.6
2.8
3
3.2
3.4
3.6
3.8
4
4.2
4.4
4.6
x 10
7
Fourth Cumulant, γ
4
from 0 to 0.0001, γ
2
= γ
3
= 0.001
γ
4
V
4
−Cost Cumulant Value Function
(b) V4
0 20 40 60 80 100
−1
0
1
2
3
4
5
6
7
x 10
6
192 Neural network weights
Time(sec)
Neural Network Weights
Neural Network Weights 1 to 192
(c) Weights
Figure 1: Value Functions and Neural Network Weights.
problem. Statistical control shapes the cost cumulants
to improve the performance of the controller. We de-
rived the necessary condition for minimizing the n-th
cost cumulant for a givensystem. By shaping the den-
sity function, we improve the system performance.
The HJB equation for the n-th cumulant minimiza-
tion is derived. The optimal controller for the n-th
cumulant minimization problems is found by solving
the corresponding HJB equations. The n-th cumulant
HJB equation is numerically solved using neural net-
work method. In the satellite attitude control problem,
the performance is shaped using the Lagrange multi-
plier, which decreased the fourth cumulant, while the
first cumulant increased.
ACKNOWLEDGEMENTS
This material is based upon work supported in part by
the National Science Foundation AIS Grant, ECCS-
0969430.
REFERENCES
Alberkht, E. G. (1961). On the Optimal Stabilization of
Nonlinear Systems. PMM - Journal of Applied Math-
ematics and Mechanics, 25:1254–1266.
Beard, R., Saridis, G., and Wen, J. (1997). Sufficient Con-
ditions for the Convergence of Galerkin Approxima-
tions to the Hamilton-Jacobi Equation. Automatica,
33(12):2159–2177.
Chen, T., Lewis, F. L., and Abu-Khalaf, M. (2007). A Neu-
ral Network Solution for Fixed-Final Time Optimal
Control of Nonlinear Systems. Automatica, 43:482–
490.
Fleming, W. H. and Rishel, R. W. (1975). Determinis-
tic and Stochastic Optimal Control. Springer-Verlag,
New York.
Kang, B. and Won, C. (2010). Nonlinear Second Cost
Cumulant Control using Hamilton-Jacobi-Bellman
Equation and Neural Network Approximation. In
Proc. of the American Control Conference, Baltimore,
MD.
Lim, A. E. and Zhou, X. Y. (2001). Risk-Sensitive Control
with HARA Utility. IEEE Transactions on Automatic
Control, 46(4):563–578.
Sain, M. K. (1966). Control of Linear Systems According
to the Minimal Variance Criterion—A New Approach
to the Disturbance Problem. IEEE Transactions on
Automatic Control, AC-11(1):118–122.
Sain, M. K. (1967). Performance Moment Recursions, with
Application to Equalizer Control Laws. In Proc. of
Annual Allerton Conference on Circuit and System
Theory, Monticello, IL.
Smith, P. J. (1995). A Recursive Formulation of the Old
Problem of Obtaining Moments from Cumulants and
Vice Versa. The American Statistician, 49(2):217–
218.
Stuart, A. and Ord, J. K. (1987). Kendall’s Advanced The-
ory of Statistics:Distribution Theory. Oxford Univer-
sity Press, New York, 5th edition.
Won, C., Diersing, R. W., and Kang, B. (2010). Sta-
tistical Control of Control-Affine Nonlinear Systems
with Nonquadratic Cost Function:HJB and Verifica-
tion Theorems. Automatica, 46(10):1636–1645.
Won, C.-H. (1999). Comparative Study of Various Con-
trol Methods for Attitude Control of a LEO Satellite.
Aerospace Science and Technology, 3(5):323–333.
PerformanceShapingthroughCostCumulantsandNeuralNetworks-basedSeriesExpansion
201
