Motorbike Modeling and Control

ao Sequeira and Marco di Vittori

Instituto Superior Tecnico, Technical University of Lisbon, Lisbon, Portugal

Keywords:

Kinematics, Dynamics, PID Control, MPC Control, Nonlinear Control.

Abstract:

This paper surveys the kinematics of bikes and details the construction of a dynamics model for a motorbike

using the Lagrangian approach. Using data from a typical sports motorbike, a dynamics model is obtained by

symbolic computation. This model, of high algebraic complexity, is then wrapped as a function and used for

control purposes. Control strategies based on PID, MPC, and nonlinear control are discussed and simulation

results for each of them are presented.

1 INTRODUCTION

The study of bicycle modeling and control dates back

to the last years of 19th century, namely through the

work of F.J. Whipple (see for instance (Limebeer and

Sharp, 2006)). In recent times there has been a re-

newed interest in this type of vehicles from an aca-

demic viewpoint and extreme riding, as in racing,is

still challenging, namely in what concerns the devel-

opment of control strategies for autonomous or quasi-

autonomous motion.

Related work in literature is extensive. Surveys

on a wide range of bicycle models are presented in

(Astr

om et al., 2005), (Limebeer and Sharp, 2006). A

linearized model for an uncontrolled bicycle was pre-

sented in (Schwab et al., 2004) with multiple simpli-

ﬁcations, namely the bike is formed by rigid bodies,

the wheels have no width, and the rider position is

constant.

Realistic motorcycle dynamics have an alge-

braically complexity higher than those of simple by-

cicles. Among the relevant work, the geometry of

the contact between tyres and the road, the tyre shear

force and moment descriptions, as functions of load,

slip and camber, the tyre relaxation properties, rear

suspension, rider behavior, and steering control have

been addressed in (Sharp et al., 2004). Only PID

based strategies were considered for speed and steer-

ing control, though with adjustable gains.

Some aspects related to the steering angle con-

trol in human driving are addressed in (Popov et al.,

2010). The stability dependency on control param-

eters is analyzed from the human automatisms pro-

cesses when riding a motorbike, including a precog-

nitive component related to the rider’s experience, a

compensatory component as the closed loop control,

and a pursuit component as a feedforward term to

handle throttle and braking. Optimal, Model Pre-

dictive (MPC), and PID based steering control are

claimed to match the three stage control used by hu-

man riders.

This paper surveys kinematics models for byci-

cles and their extensions to commercial motorbikes in

section 2. The dynamics model is derived in section

3, using the classic constrained Lagrangian method.

This model is then used in section 4 to test trajectory

tracking using PID, MPC, and nonlinear laws. Simu-

lation results are compared with a reference trajectory

obtained from telemetry data from a real motorbike in

a racetrack. Section 5 discusses the results obtained

with the models based uniquely on the kinematics and

those obtained using dynamics models.

2 KINEMATICS

Using the simpliﬁed geometry in ﬁgure 1 the kine-

matics equations for a simple motorbike model are

simply, (Limebeer and Sharp, 2006),

˙x = v cos(ψ) (1)

˙y = v sin(ψ) (1a)

ψ =

vtan(δ)

wcos(ϕ)

(1b)

where w is the wheelbase, assumed constant.

The rake angle, γ (see ﬁgure 2) can be easily in-

cluded and (1b) becomes,

249

Sequeira J. and di Vittori M..

Motorbike Modeling and Control.

DOI: 10.5220/0004034302490254

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 249-254

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

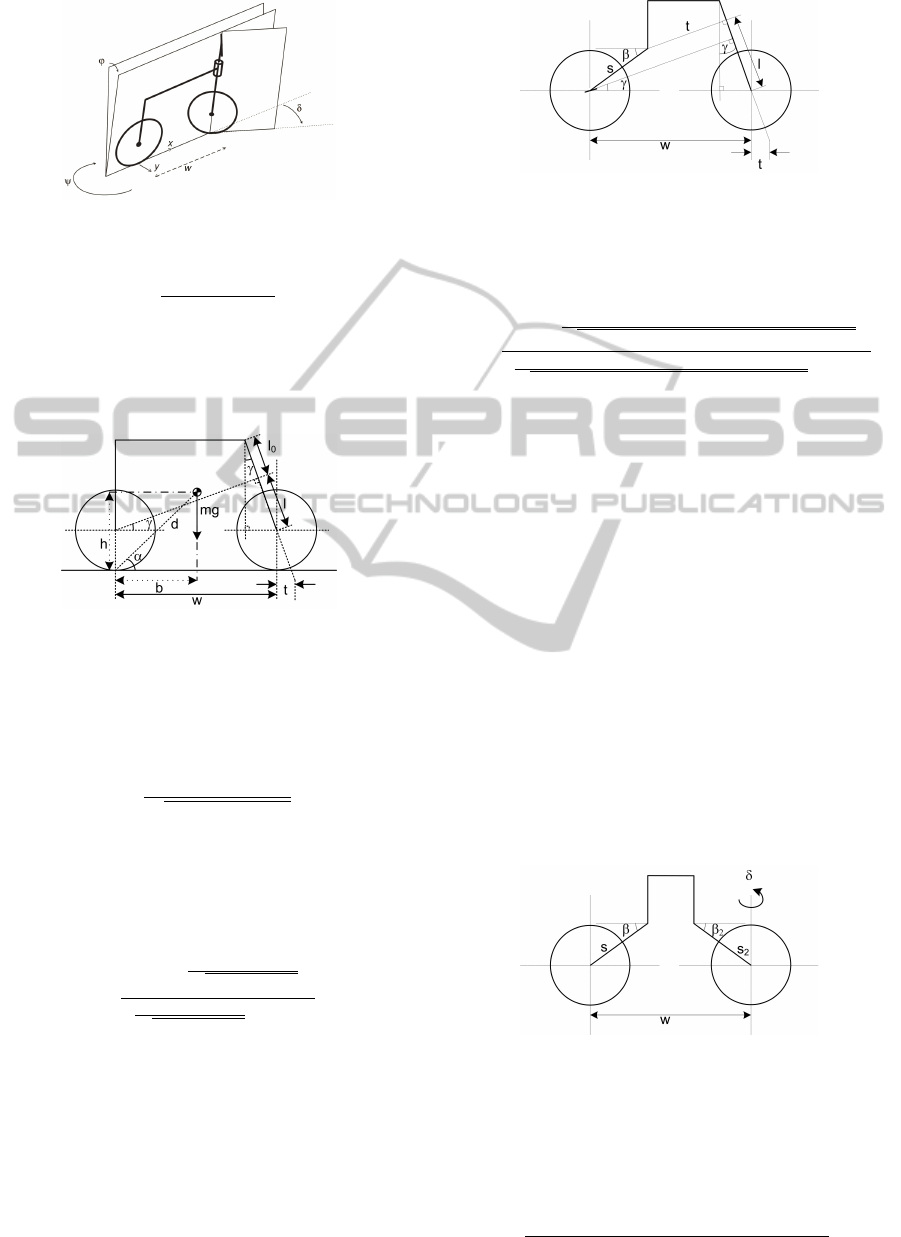
Figure 1: Simpliﬁed bike geometry (adapted from (Lime-

beer and Sharp, 2006)).

ψ =

vtan(δcos(γ))

wcos(ϕ)

(2)

A typical rake in resting conditions value for a com-

mercially available motorbike is γ = 23.5

◦

. This

model assumes no front or rear suspensions which in

reality induce variations in w.

Figure 2: Front fork, rake angle, and trail distance.

The front fork length is given by l = w sin(γ) (see

ﬁgure 2). Assuming that the chassis is rigid w cos(γ)

must be constant

It is straightforward to obtain the following rela-

tion,

w =

cos

(γ

) + l

(3)

where w

and γ

represent the wheelbase distance and

rake angle in resting conditions. Substituting in (2)

the kinematics model including the front fork length l

is,

ψ =

v tan



cos(γ

√

cos

(γ

)+l



√

cos

(γ

)+l

cos(ϕ)

(4)

A typical value for the front fork trail is around 119.0

mm.

In most of the current motorbikes the rear wheel is

connected to the chassis through a moving swingarm.

The typical geometry used by manufacturers intro-

duces a new variable, β, representing the angle be-

tween the swingarm and the horizontal x axis (ﬁgure

3). The length of the swingarm is denoted by s.

The corresponding model can be obtained by replac-

Figure 3: Swingarm connecting the back wheel to the bike

frame.

ing the variables w

and γ

in (4) by w

−(s −cos(β−

)) and l + sin(β −γ

) respectively.

ψ =

v tan



|(w

−(s−cos(β−γ

)))cos(γ

√

−(s−cos(β−γ

)))

cos

(γ

)+(l+sin(β−γ

))



(l+sin(β−γ

))

√

−(s−cos(β−γ

)))

cos

(γ

)+(l+sin(β−γ

))

cos(ϕ)

(5)

Model (5) accounts for most of the geometric as-

pects in current motorbike designs. Even though the

instantiation done with typical values for some of the

parameters, the model shows the complex structure of

a motorbike kinematics.

From (1) and (2), if w increases then

ψ decreases.

This may be a desirable feature in conditions where

ψ is subject to disturbances. For example, under hard

braking conditions any disturbances in δ and v will be

affected by the gain 1/w. If this gain decreases then

also will the effects of these disturbances in ψ.

A similar reasoning can be made when the front

fork is considered and this suggests an alternative

kinematics, namely using and additional swingarm at

the front of the motorbike, instead of the common

front fork. In terms of the model previously devel-

oped there is no γ angle and an additional variable

is introduced to represent the angle of the front

swingarm.

Figure 4: Double swingarm geometry.

As before, using typical values from commer-

cially available motorbikes yields or the rotation (w

now depends on both the front and rear swingarm po-

sition),

w = s cos(β) + s

cos(β

) + 231

ψ =

v δ

578.5(cos(β) + cos(β

) + 231)cos(ϕ)

(6)

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

250

where β and β

values will be in the range

[0.4

◦

,13.4

◦

Double swingarm kinematics has been seldom

used in production bikes (the reader can check the

Yamaha GTS 1000 and Bimota Tesi). Even in rac-

ing applications, which in a sense tend to use more

extreme designs, there is a single known case, the Elf

500cc motorbike, which raced during the 80’s decade.

This type of kinematics is sometimes referred as be-

ing extremely stable under hard braking conditions.

Combinations of the fork and swingarm in the

front geometry are currently being used (see for in-

stance the telelever and duolever systems used by

BMW). As aforementioned, the idea is to increase the

wheelbase under braking to improve the rideability.

3 DYNAMICS

Computing the dynamics of a constrained multibody

vehicle, as a motorbike, is relatively straightforward

assuming that the motorbike is composed by multiple

rigid bodies with known geometry and mass distribu-

tion properties. However, it is seldom the case that

perfect information is available. An extreme example

is the sloshing effect caused by the fuel moving freely

in the tank (in some bikes the fuel can account for 6%

of the total mass). Therefore, simpliﬁed models of

mass distribution are often assumed.

The strategy followed in this paper is to compute a

symbolic model, using the Lagrangian technique. The

resulting model is then wrapped as a Matlab func-

tion that can be used as a blackbox model for ex-

perimenting purposes. This model accounts for the

main kinetic energy sources in a motorbike, namely,

the engine, and wheels and bike main body under

leaning and turning (the terms due to the motion of

the swingarm and front fork are not considered). Po-

tential energy is also not considered in this model as

the variations involved when the bike leans or moves

along height variations tend to be small and do not

disturb the structure of the model.

The total kinetic energy including terms due to

leaning and turning, linear velocity, front and rear

wheels, and engine is thus given by,

K =

ϕh +

ψb)

+ (7)

4cos

(δcos(γ))

where b,h are the mass center coordinates (see Fig-

ure 2, note that the total mass of the frame, suspen-

sions, and non-rotating parts of the engine, m, are

concentrated at a single point). The front and back

wheels have masses m

and m

, respectively, and

is the engine’s rotating mass and inertias mod-

eled as thin disks. The wheel radius are r

and r

respectively for the front and back wheels, whereas

is the radius of the engine’s rotating mass. The

angular velocity of the engine is

leading to an-

gular velocities for the forward and back wheels of

cos(δ)R

and

= g

, respectively. The ra-

tio between the engine and rear wheel angular ve-

locities is denoted g

and R

is the rear wheel effec-

tive radius which accounts for the leaning of the bike

as R

= r

cos(ϕ) + r

1 −(r

sin(ϕ))

and r

the wheel rhym radius, r

is the tyre tube radius and

= r

+ r

Table 1 lists the main physical parameters and val-

ues used in the model.

Table 1: Dynamics parameters (after a commercial motor-

bike).

α = 0.698rad d = 0.85m m = 180Kg

= 3.3Kg m

= 4.5Kg m

= 2.5Kg

= 0.3149m r

= 0.1m g

= 0.192

= 0.2277m λ

= 23.5

◦

The theory for constrained Lagrangian systems is

well understood when the constraints are holonomic

or semi-holonomic. See for instance (Chess

e and

Bessonet, 2001; Campion et al., 1996; McClamroch

and Wang, 1988) for structures with holonomic con-

straints and (Flannery, 2005) for nonholonomic ones.

The ideal 2-wheel motorbike has two classes of

constraints, (i) the contact with the ground which

constrains the vertical movement, and (ii) the car-

like non-holonomic constraint, v =

ψr

(which is also

commonly written as ˙x sin ψ − ˙y cos ψ = 0), that in-

hibits side-slipping (r

represents the curve radius)

and the rolling constraint v = cos(ψ) ˙x + sin(ψ) ˙y, that

inhibits forward-skidding. In a real motorbike the va-

riety of situations rends difﬁcult an accurate identi-

ﬁcation of the constraints. For example, the geome-

try of the contact between the tyres and the ground

imposes that there is indeed a small amount of slide-

slippage and hence the non side-slipping constraint is

only valid under unrealistic conditions.

A common strategy when identifying constrained

dynamics is to rely on a priori knowledge on the

physical effects affecting the robots (see for instance

(Astr

om et al., 2005; Yi et al., 2009)). The con-

straining torques are thus simpliﬁed and are consid-

ered the direct consequence of the reaction forces ap-

plied on the center of mass and formed by the gravi-

tational and centrifugal forces that constrain the mo-

MotorbikeModelingandControl

251

torbike at the contact points between the wheels and

the ground. These forces are calculated as N = mg

and T = m R

ψ, respectively as the vertical force

due to gravity depending on the total mass, m, and

gravity g and the centrifugal force due to

ψ turning

speed. These forces are related to ϕ as the torque

ϕext

= Nh sin(ϕ) −T h cos(ϕ) so the total model has

the following structure.





+V =







Nhsin ϕ −T hcos ϕ



(8)

with M and V as determined by the free Lagrangian

computed from (7), and Γ

, Γ

being functions re-

spectively of the steering angle δ and the force F

ex-

herted on the footpegs by the driver.

4 CONTROL

The dynamics model (8) was ﬁrst controlled by a PID

controller. Figure 5 shows the results obtained for

a section of the Montmelo racetrack near Barcelona,

Spain. This section of the racetrack includes fast

and slow portions where different control parameters

are required. Thus, a supervisor controller changes

the PID gains at appropriate times, when the bike

switches between the different sections of the track.

Figure 5: PID based control.

A natural alternative approach, widely used in the

literature (see for instance (Rau and Schr

oder, 2002))

is the Model Predictive Control (MPC). Roughly, the

MPC computes the open loop controls during a ﬁ-

nite horizon that minimize at each instant k a cost

J(k) =

∑

i=1

(r(k + i) −y(k + i))

+ w

∑

i=1

u(k +

, where r is a reference, y the output and u the con-

trols of the system, and uses the ﬁrst controls in the

optimal sequence. At subsequent steps the procedure

is repeated, thus closing the control loop.

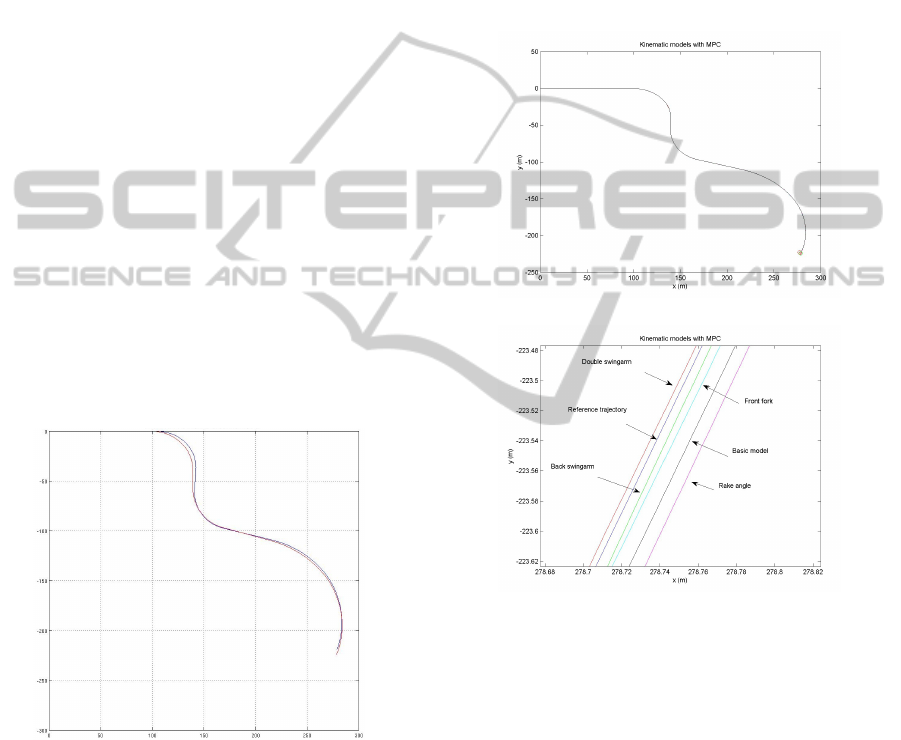
Figure 6 shows the MPC applied to the kine-

matic models described in previous section, (1) to

(6). A discrete range of controls is used, namely

δ ∈

{

−1,−0.5,−0.2, 0,0.2, 0.5,1

}

. Linear velocity is

assumed constant, v = 1, and wheelbase w

= 1.3m.

Control horizon N = 3 N

= N

= 3 and control

weights are w

= 10 and w

= 2 ×10

−4

for the sim-

pler models and w

= 10

−8

for model (5). Only the

ﬁrst control of the sequence computed at each instant

is used, that is, a new control is computed at each time

step.

(a) Complete trajectory

(b) Trajectory detail

Figure 6: Kinematic models with MPC.

Even though the trajectories are shown for ﬁxed

values of the parameters λ

,l,β,β

, the curves sug-

gest that the double swingarm and front fork models

may be preferable in a real racing scenario, where the

small differences shown may be very relevant.

Figure 7 illustrates the MPC results when the full

dynamics model is used with w

= 10 and w

= 10

−4

PID control was used to drive the leaning to 0 and an

engine torque bounded at 0.8 Nm.

The nonlinear law used to control steering is com-

mon in Robotics (and known to stabilize linearized

unicycle models) and is of the form,

δ = −K

vl + K

|v|(ψ

re f

−ψ) (9)

where l is the signed distance deﬁned by the projec-

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

252

(a) Trajectory

(b) Steering angle

Figure 7: Dynamics model and MPC.

tion of the position of the motorbike onto the refer-

ence path, v is the linear velocity, ψ, ψ

re f

are the ori-

entation of the bike and the corresponding reference,

and K

, K

tuning constants. Leaning was controlled

using a PID.

Figure 8 illustrates the performance of the motor-

bike when the steering is controlled by (9) (see ap-

pendix 5 for a stability proof).

The jerk in both controls is signiﬁcantly smaller

than with MPC control and the leaning angle error is

also smaller.

5 CONCLUSIONS

Starting from basic models for bicycles, the paper

introduces a number of kinematics features that are

common in motorbikes. These features are shown

to inﬂuence the kinematic models signiﬁcantly and

hence justify the use of complex models to describe

bikes in the context of real applications. MPC control

was shown to yield small differences among the mod-

els that nonetheless may be relevant in extreme riding

conditions such as racing.

A dynamics model, accounting for the bike and

engine motion, is presented and controlled using PID,

(a) Trajectory

(b) Steering angle

Figure 8: Nonlinear control law with K

= 5, K

= 10.

MPC, and a nonlinear law. As with the kinematic

models, the three techniques show very small differ-

ences in the trajectory following error, though pre-

senting very different computational requirements.

Even though the simplifying assumptions taken,

i.e., on point masses, inertias, rigidity of the different

bodies, driver model reduced to the footpeg force in-

put, the algebraic complexity of the free Lagrangian

is high. This justiﬁes the use of a further simplifying

strategy, that is, the inclusion of constraint forces di-

rectly in the model. The different control strategies

provide interesting results, with the nonlinear law ex-

hibiting a far more reasonable behavior from a practi-

cal application perspective, with less jerk, and suggest

that the whole model can be used to further proceed

the research on the full racing problem. Future work

also involves the testing of a supervisory control layer

to optimize the selection of parameters for the leaning

and velocity loops.

ACKNOWLEDGEMENTS

This work was partially supported by FCT project

PEst-OE/EEI/LA0009/2011.

MotorbikeModelingandControl

253

REFERENCES

Abdallah, C., Dawson, D., Dorato, P., and Jamshidi, M.

(1990). Survey of Robust Control for Rigid Robots.

In Procs. American Control Conf.

Anderson, R. (1989). Passive Computed Torque Algorithms

for Robots. In Procs. 28th Conf. on Decision and Con-

trol.

Astr

om, K., Klein, R., and Lennartsson, A. (2005). Bicycle

Dynamics and Control. IEEE Control Systems Maga-

zine.

Campion, G., Bastin, G., and D’Andrea-Novel, B. (1996).

Structural Properties and Classiﬁcation of Kinematic

and Dynamic Models of Wheeled Mobile Robots.

IEEE Trans. on Robotics and Automation, 12(1).

Chess

e, S. and Bessonet, G. (2001). Optimal dynam-

ics of constrained multibody systems. Application to

bipedal walking synthesis. In Procs of the IEEE Int.

Conf. on Robotics and Automation. Seoul, Korea, May

21-26.

Flannery, M. (2005). The enigma of nonholonomic con-

straints. American Journal of Physics, 73(3):265–272.

Limebeer, D. and Sharp, R. (2006). Bicycles, Motorcycles,

and Models. IEEE Control System Magazine.

McClamroch, N. and Wang, D. (1988). Feedback Stabi-

lization and Tracking of Constrained Robots. IEEE

Transactions on Automatic Control, 33(5):419–426.

Ortega, R., Lor

ıa, A., Nicklasson, P., and Sira-Ram

ırez, H.

(1998). Passivity-based Control of Euler-Lagrange

Systems. Springer.

Ortega, R. and Spong, M. (1988). Adaptive motion con-

trol of rigid robots: A tutorial. In Procs. IEEE Conf.

Decision and Control.

Popov, A., Rowell, S., and Meijaard, J. (2010). A review

on motorcycle and rider modeling for steering control.

Vehicle System Dynamics, 48(6):775–792.

Rau, M. and Schr

oder, D. (2002). Model Predictive Control

with Nonlinear State Space Models. In Procs. of the

American Control Conference (AMC 2002).

Schwab, A., Meijard, J., and Papadopoulus, J. (2004).

Benchmark results on the linearized equations of mo-

tion of an uncontrolled bicycle. In Proc. 2nd Asian

Conf. Multibody Dynamics.

Sharp, R., Evangelou, S., and Limebeer, D. (2004). Ad-

vances in the Modeling of Motorcycle Dynamics.

Multibody System Dynamics, (12):251–283.

Yi, J., Zhang, Y., and Song, D. (2009). Autonomous Motor-

cycles for Agile Maneuvers, Part I: Dynamics Model-

ing. In Procs. Joint 48th IEEE Conf. on Decision and

Control and 28th Chinese Control Conf.

Yu, H. and Antsaklis, P. (2009). Passivity-Based Distributed

Control of Networked Euler-Lagrange Systems With

Nonholonomic Constraints. Technical report. Tech-

nical Report of the ISIS Group at the Univ. of Notre

Dame, ISIS-09-003.

APPENDIX

Nonlinear Controller Stability

The dynamics (8) can be written in more general

terms as,

M(ϕ,θ)





+V (ϕ,

ϕ,θ,

θ) = (10)



2.148F





Nhsin(ϕ) −T h cos(ϕ)



ψ = 0.046 tan(δcos(γ))

θ/cos(ϕ) (10b)

Unconstrained Lagrangian systems can be shown

to have the passivity property, (Ortega and Spong,

1988) even when subject to external forces/torques,

such as the case of a motorbike, (Yu and Antsaklis,

2009). Also, a feedback control of a passive system

with a passive controller yields a stable system (see

(Abdallah et al., 1990)) and even in the case of con-

tact forces and uncertainties in M a PD-like structure

was shown to be able to stabilize the system (see (An-

derson, 1989)).

Therefore, it remains to be shown here that (i) de-

coupling the control for F

,δ does not disturb the

passivity property, and (ii) the nonlinear law (9) also

drives the tracking error to zero.

The passivity property is closed under the addi-

tion operation on controls. In what concerns con-

trol inputs F

, decoupling the control law means

that each control input is driven by an independent

controller. In the experiments, T

was chosen as a

pulse of constant height 0.1 Nm, going to zero as

> 0.8 rad/s and hence it veriﬁes the passivity prop-

erty. As for F

, it was generated after a PID, meaning

that it also veriﬁes the passivity property (see (Ortega

et al., 1998)). It is enough to described the control

as [Γ

,Γ

] = [Γ

,0] + [0, Γ

] to verify that the decou-

pling of the controls preserves the passivity property

of the overall system.

As for the control input δ, substituting the control

law (9) in (10b) yields an equation of the form,

˙e

= −tan



(−K

vl + K

|v|e

)cos(γ)



K (11)

where the orientation error is e

= ψ

re f

−ψ, and K =

0.046

θ/cos(ϕ) is nonzero for the relevant ranges of

the argument, i.e., v ∈(0,+∞) and ϕ ∈ (−pi/2, π/2).

The ﬁxed point of (11) is thus obtained either

when v = 0, or when l = 0 and ψ = ψ

re f

, and hence

the nonlinear control law is able to make the motor-

bike track the reference trajectory.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

254