Homomorphic Primitives for a Privacy-friendly Smart Metering

Architecture

Benjamin Vetter

, Osman Ugus

, Dirk Westhoff

and Christoph Sorge

Department of Computer Science, HAW Hamburg, Hamburg, Germany

Department of Computer Science, University of Paderborn, Paderborn, Germany

Keywords:

PET for Smart Metering, Homomorphic MACs, Homomorphic Encryption.

Abstract:

We propose a privacy-friendly smart metering architecture which is yet ﬂexible enough to serve various future

third party energy services. Our secure architecture may be deployed as a cloud service and allows processing

of SQL queries on encrypted measurements, providing aggregated results in a most ﬂexible manner. A com-

bination of homomorphic encryption and homomorphic MACs provides conﬁdentiality of the users’ energy

consumptions, allowing integrity checks and enhanced SQL-queries on encrypted data. Our extensive perfor-

mance analysis shows that our approach is promising with respect to storage and computational overhead.

1 INTRODUCTION

In the future energy market, millions of smart me-

ters will measure consumers’ electricity consumption.

At the backend, we expect a management system

which collects these readings. The system must, on

one hand, provide sufﬁcient information to the grid

and energy providers. On the other hand, individual

consumption details must be kept secret. We solve

the ﬁrst problem by allowing aggregation of the con-

sumed energy at various scales. Policies for access to

the data at different granularities can be deﬁned by a

regulator or negotiated between the entities involved.

For example, a grid provider may need precise infor-

mation about speciﬁc regions only due to bottlenecks

in the transfer network. Thus, an energy management

system should consider concrete business cases with

respect to the policies agreed upon between each of

the energy services like e.g., energy demand forecast-

ing or grid optimization services. A smart metering

architecture typically involves the following entities:

The

Energy Provider (EP)

sells energy and

provides price information to its customers which

is used by the home automation systems to manage

home appliances with the overall objective of saving

energy and reducing the overall costs. Today, an EP

buys energy for a certain point in time based on stan-

dard load curves for private customers. A smart me-

tering architecture, on the other hand, allows precise

accounting. Based on its customers’ total energy de-

mand at a speciﬁc time, the EP can buy energy, make

forecasts and control the production of electricity.

The

Gateway (GW)

connects smart meters to the

smart grid. It is responsible for collecting smart me-

ter data as well as securing the collected data before

sending it to the GP via a Wide Area Network.

The

Grid Provider (GP)

is responsible for the

grid and for passing aggregated energy consumptions

received from GWs to the EP for planning purposes.

Moreover, the GP is responsible for providing energy

consumptions of individual customers to the EP, nec-

essary for billing purposes. The GP itself needs to

know accurate energy consumptions of all customers

in a certain region to optimize its network. Finally, ac-

cording to e.g., the German Energiewirtschaftsgesetz

(EnWG, 2005), smart meters are installed, operated,

and maintained by the GP or a third party authorized

by the GP. Thus, we assume that smart meters are ex-

clusively installed and operated by the GP.

Smart Meter

is responsible for measuring the

energy consumption of a customer and reporting it to

the GP through the GW. However, we assume that the

GW and smart meter are combined in a single device.

2 PRIVACY AND FLEXIBILITY

Typically, every 15 minutes, a smart meter reports a

customer’s energy consumption. Detailed reports al-

low to forecast energy demands more precisely and to

optimize its production. Customers can analyze and

102

Vetter B., Ugus O., Westhoff D. and Sorge C..

Homomorphic Primitives for a Privacy-friendly Smart Metering Architecture.

DOI: 10.5220/0004036601020112

In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 102-112

ISBN: 978-989-8565-24-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

optimize their energy usage to save costs. However,

detailed energy reports allow to create customer pro-

ﬁles. Anyone who knows the ﬁne-grained consump-

tions can infer the customer’s habits like e.g., absence

and even concrete activities like watching TV (Enev

et al., 2011). Consequently, a smart metering archi-

tecture ideally has to protect customer privacy while

at the same time providing all beneﬁts of smart me-

ters by allowing detailed energy measurement reports

of customers. A smart metering architecture needs

to process millions of energy consumptions. The

databases used for such a purpose may easily run out

of space or become too slow to respond to extensive

queries. GPs may want to outsource them to a cloud

provider to be able to dynamically scale the infras-

tructure according to their requirements. However,

outsourcing the processing of personal data is prob-

lematic from a legal perspective (European law, e.g.,

restricts the export of personal data). Moreover, data

leaks at the cloud provider causes damage to the GP’s

public image even if there are no legal consequences.

Thus, the cloud provider may at no time be able to

learn energy consumptions of individual customers

such that e.g., all consumptions have to be stored en-

crypted in the database. However, one must still be

able to aggregate the consumptions without the need

to ﬁrst decrypt them, because decrypting them would

imply a huge computational burden. Homomorphic

encryption schemes are perfectly suited for this sce-

nario. They allow to perform certain operations on

ciphertexts directly where the operation corresponds

to an operation performed on the plaintexts.

3 RELATED WORK

A number of technical approaches have been sug-

gested to protect customer privacy in smart meter-

ing. (Bohli et al., 2010) present a privacy model for

smart metering and two approaches with and with-

out a trusted third party. In the former approach, a

trusted proxy aggregates the electricity measurements

of all smart meters. This approach does not scale well

for large smart grids. The latter approach is based

on adding a random noise to the meter measurements

which sums up to zero in the ﬁnal aggregation. How-

ever, the precision is acceptable only for large groups

of meters. In (Kursawe et al., 2011), a number of

protocols for privacy-preserving aggregation are pre-

sented, based on distributing secrets to smart meters

that add up to a known value. (Efthymiou and Kalo-

gridis, 2010) propose to report privacy critical, ﬁne-

grained measurements using anonymous identiﬁers.

Low-grained measurements are reported with known

smart meter identiﬁers. However, the following secu-

rity issue remains: The sum of ﬁne- and low-grained

energy measurements must be equal. Hence, an at-

tacker having these measurements can still ﬁnd rela-

tionships between them. The use of homomorphicen-

cryption has been suggested by several authors. (Gar-

cia and Jacobs, 2010) suggest a provably secure pro-

tocol that allows the energy supplier to learn only

an aggregate value by using a combination of addi-

tively homomorphic encryption and additive secret

sharing. In every reporting period, every meter per-

forms n − 1 encryptions and a decryption for the ag-

gregation of measurements from a group of n smart

meters. This causes a huge overhead on the smart

meters. (Li et al., 2010) propose to use other smart

meters as intermediate hops which aggregate the ho-

momorphically encrypted meter data. Smart meters

are arranged in a tree structure, where the collec-

tor node is the root node. Thus, such a required di-

rect communication among smart meters is the main

drawback of this scheme. Recently, (McLaughlin

et al., 2011) proposed to place a battery between

a smart meter and the circuit breaker. The battery

allows to smooth the load curve, such that analyz-

ing algorithms can no longer detect certain events

within the curve. Other approaches include encrypted

databases and secure multi party computation. Un-

less the encryption mechanism is additively homo-

morphic, an encrypted database like OPES (Agrawal

et al., 2004) does not allow the aggregation of en-

crypted data. Hence, decryption of data is required

which again increases the overhead. Concepts from

multi party computation are applied for privacy pre-

serving data mining over databases by (Ben-Or et al.,

1988) and (Chaum et al., 1988). However,such mech-

anisms come with high storage and communication

overheads due to replica and the communication re-

quired between them. While the aforementioned sug-

gestions focus on privacy-aware aggregation of meter

readings, (Rial and Danezis, 2011) show how to use

a smart meter to securely compute electricity bills on

the meters without revealing the consumption data.

Besides the scientiﬁc community, smart grid pri-

vacy issues are also discussed by government agen-

cies. In the US, the NIST issued ”‘guidelines for

smart grid cyber security”’, including privacy recom-

mendations (NIST11, 2010). A focus is on secur-

ing access to meter data and limiting the collection of

data. In Germany, the (Federal Ofﬁce for Information

Security, 2011) proposes a pseudonymization of cus-

tomers to protect their privacy. This approach is sim-

ilar to (Efthymiou and Kalogridis, 2010) and hence

suffers from the security problems discussed above.

HomomorphicPrimitivesforaPrivacy-friendlySmartMeteringArchitecture

103

4 OUR CONTRIBUTIONS

We propose a smart metering architecture which is

both privacy-friendly and ﬂexible to serve various

future energy services. Consumer privacy is pre-

served by encrypting energy consumptions with an

efﬁcient additively homomorphic encryption mecha-

nism allowing their aggregation without decrypting

them ﬁrst. Smart meters encrypt the consumptions

and send them to the energy managementsystem. The

encrypted measurements are stored in a database, al-

lowing aggregation over time, region, or other selec-

tion criteria with various selective SQL-queries. Our

protocol requires a trusted third party, but its pri-

mary task is to hand out a set of keys to each smart

meter used for encrypting consumption values. The

keys can be used for a long time and thus, the third

party is less frequently involved. Finally, we empha-

size that most of the proposed approaches like (Bohli

et al., 2010), (Garcia and Jacobs, 2010) and (Li et al.,

2010) require to perform the aggregation either on a

smart meter, in the smart grid or on a trusted third

party which limits their ﬂexibility. Using these proto-

cols, the ﬁne-granular energy measurements are sub-

sequently unavailable to the energy services. In con-

trast, our approach permits the aggregation of data

outside the grid even in the cloud using various selec-

tive SQL-queries, supporting third party energy ser-

vices and various types of new energy businesses.

5 SECURE ARCHITECTURE

Our smart metering architecture consists of a key au-

thority (KA), an energy management system (EMS), a

set of customersC and a set of services S = {s

,..,s

}

representing the GP, EP and other services. Every

entity allowed to query the EMS for encrypted con-

sumptions is denoted as a service in our architecture.

We denote by e

sid, j

the electricity consumption mea-

sured by smart meter sid for period j.

The KA is responsible for managing certiﬁcates

and keys for smart meters. It can be e.g., a Certiﬁcate

Authority. As the main requirement, the KA should

be a trusted third party. We assume that certiﬁcates

and keys required in our architecture are generated

and stored in a smart card. The smart card is sub-

sequently sent to the customer by mail. If no smart

cards can be used, the keys must safely arrive at the

customers to be securely stored in the meters.

The EMS is operated by the GP and stores the en-

ergy consumptions received from all meters. The me-

ters send their encrypted measurements to the EMS

responsible for their GP. Anyone (e.g., an EP) inter-

ested in knowing energy consumptions of a certain

region queries the EMS using selective SQL queries.

Customers are grouped according to their loca-

tions, i.e. by a spatial grouping scheme. More speciﬁ-

cally, customers at the same building or neighborhood

belong to the same group. A group can be composed

of any number of customers but at least two. Larger

groups provide a higher level of privacy. We argue

that our grouping does not limit the beneﬁts of a smart

grid. For planning purposes and forecasts, an EP or

GP is primarily interested in the total consumption of

a speciﬁc region. Fine-grained knowledge about the

energy consumption of each customer is not required.

Our grouping scheme allows to precisely compute the

total energy consumption of certain buildings, neigh-

borhoods, cities, etc. Other grouping schemes like

e.g., temporal grouping schemes, are also possible.

However, they require the measuring periods to be

sufﬁciently large to preserve the customers’ privacy.

Such a grouping scheme can be used for e.g., billing.

Spatial and temporal groupingcan also be used in par-

allel to support various energy services.

5.1 Homomorphic Encryption Scheme

Requirements

- In our architecture a service (EP,

GP, etc.) queries the EMS for the total energy con-

sumption of a group of smart meters located in the

same geographical region. The energy measurements

stored in the EMS are encrypted and their individ-

ual decryptions are not allowed. Hence, decryption

must be performed on the aggregated ciphertexts.

That is, the querier should be able to decrypt a sum

of ciphertexts but not the individual ciphertexts in-

cluded in that sum. Suppose Enc

() is an encryp-

tion function and Dec

() is the corresponding decryp-

tion function using a key k. Let E denote a message

space such that e

∈ E and K a key space such

that k,k

∈ K. We term Enc

() additively homo-

morphic if there is a ⊗ and k = f(k

) such that

Dec

(Enc

) ⊗ Enc

)) = e

+ e

. Such an en-

cryption scheme thus allows to calculate the encryp-

tion of the sum of plaintexts from the corresponding

individual ciphertexts without ﬁrst decrypting them.

Candidates

- An overview of asymmetric homo-

morphic schemes can be found in (Mykletun et al.,

2006). We argue that for an equivalent level of

security, asymmetric schemes are generally less ef-

ﬁcient than symmetric ones. Hence, we consider

merely symmetric homomorphic encryption schemes

in our evaluation. A symmetric scheme was proposed

by (Domingo-Ferrer, 2002). Although this scheme

employs mechanisms typically found in asymmetric

schemes, it is classiﬁed to be symmetric as the same

SECRYPT2012-InternationalConferenceonSecurityandCryptography

104

key is used for de- and encryption. This scheme is

provably secure against ciphertext-only attacks, but

insecure against known-plaintext attacks. Moreover,

this scheme only allows the aggregationof ciphertexts

that have been encrypted under the same key. Thus,

any entity that is allowed to decrypt the sum of ci-

phertexts can also decrypt the individual ciphertexts

involved in that sum. This is the main limitation of

this scheme for its use in a smart metering system,

as the privacy requirements obligate the decryption of

the sum of ciphertexts only. Finally, compared to the

candidate below, it is costly in terms of computational

overhead. Another scheme was proposed in (Castel-

luccia et al., 2005). It is similar to the one-time pad,

thus, with a proper key management, provides perfect

secrecy and is highly efﬁcient. The security of this

scheme relies on a key-stream generating a random

key for the encryption of each message. To subse-

quently decrypt an aggregate of ciphertexts, one must

know all the keys used for the individual encryptions.

Fortunately, this is not a burden for its application in

our architecture, since the aggregation of energy con-

sumptions is always performed at the group level and

all smart meters belonging to the groups are known in

advance. Any service allowed to decrypt the ciphered

aggregates of a group needs to know only the group

key, i.e. the aggregate of the group members’ individ-

ual keys. This is actually due to the main advantage of

this scheme in the context of the smart metering ap-

plication: The homomorphism applies not only to the

ciphertext space but also to the key space. It allows to

aggregate energy consumptions encrypted using dif-

ferent keys and to decrypt the resulting ciphertext us-

ing the aggregated key such that

Dec

(Enc

) +

Enc

)) = e

+ e

with k = k

+ k

. However, the

main limitation of this scheme is that it is prone to

a malleability attack. For instance, an attacker can

simply add an arbitrary value x to the ciphertext c,

such that c

′

= c+ x. The receiver of c

′

is subsequently

still able to decrypt c

′

, such that e.g., Dec

′

) =

Dec

(Enc

)+Enc

)+x) = e

+x. How-

ever, the receiver is not able to detect that the ci-

phertext has been modiﬁed. (Peter et al., 2007) pro-

pose a hybrid approach combining the advantages of

the aforementioned mechanisms. Encryption is per-

formed by applying both mechanisms in a cascaded

manner to remove the individual security weaknesses

of both mechanisms, namely known-plaintext as well

as malleability attacks for (Domingo-Ferrer, 2002)

and (Castelluccia et al., 2005), respectively. However,

this approach is, due to the cascading, less efﬁcient in

terms of data overhead and performance. Therefore,

we choose the scheme proposed by Castelluccia et al.

Enc

(e) = e+ k mod m and Dec

Table 1: (Agrawal and Boneh, 2009).

Sign(k

,c, i) Message c ∈ [0,m− 1],

i ∈ {1,...,n},

key k

∈ [0,m− 1]

u = G(k

), b = F(k

,i)

Output Tag t = (u· c) + b

Combine(T) T = {(c

),...,(c

)}

Output t =

∑

i=1

Verify(k

,b, y,t) Key k

, b =

∑

i=1

F(k

,i)

Messages {c

,...,c

y =

∑

i=1

u = G(k

), a = u· y

If a+ b = t output 1, otherwise 0

We protect against malleability attacks via an efﬁcient

homomorphic Message Authentication Code (MAC)

as described in the following section.

5.2 Homomorphic MAC

To mitigate malleability attacks, the querier must be

able to verify that the sum, i.e. the SQL-response,

is correctly composed of those energy measurements

sent by the meters only and not modiﬁed. A prefer-

able solution to achieve integrity and authentication

is the use of signature schemes. However, signature

schemes to be used in conjunction with the chosen

homomorphic encryption scheme must as well be ad-

ditively homomorphic such that: Sign(m

+ m

) =

Sign(m

) ⊗ Sign(m

). Unfortunately, as shown by

(Johnson et al., 2002), no such additively group-

homomorphic signature scheme can ever be secure.

Another solution offering integrity and authentication

includes MACs that provide the required additively

homomorphic property, such that MAC

+ m

) =

MAC

) ⊗ MAC

) with k = f(k

). How-

ever, a secret key must be shared between the me-

ters and the untrusted services. To mitigate this lim-

itation, we propose to generate individual MACs for

each service, such that different services get different

keys. Thus, a compromised key of a service does not

impact the security of MACs associated with other

services. Due to its simplicity and efﬁciency, we

choose the homomorphic MAC scheme recently pro-

posed (Agrawal and Boneh, 2009). As shown in Ta-

ble 1, it is composed of three algorithms (Sign, Com-

bine, Verify). While Sign computes an authentication

tag for messages, Combine implements the homomor-

phic property, and Verify is used to ﬁnally verify the

aggregated message-tag pairs. The functions G() and

F() denote a pseudo random generator and a pseudo

random function, respectively. Please note that both

functions can be implemented using e.g., AES.

HomomorphicPrimitivesforaPrivacy-friendlySmartMeteringArchitecture

105

Table 2: Encryption keys and data stored on the smart card.

Name Description

sid The smart meter id

enc

sid

A unique secret key used for the homomorphic en-

cryption scheme

priv

sid

pub

sid

), A unique key pair together with its

Certificate

sid

certiﬁcate issued by the KA, used to securely com-

municate with e.g., the EMS

ServerList IPs of servers to send measurements to and accept

commands from

pub

Certificate

The public key and certiﬁcate of the KA

5.3 Protocol Outline

We propose that all messages include a sequence

number and are signed by the sender to mitigate re-

play attacks. Signatures of incoming messages are

veriﬁed by the receiver to ensure the authenticity and

integrity. Invalid messages are dropped and the re-

ceiver does not respond to the sender. We consider

the following scenarios: (1) a GP installs a meter (2)

a customer ﬁxes a contract with an EP, (3) a customer

quits a contract with an EP, (4) a smart meter reports

its energy consumption to the EMS and (5) querying

the EMS for aggregated consumptions.

1- A GP installs a meter

: When a GP in-

stalls a meter within a building, the KA is instructed

to send a smart card issued for the sid of that smart

meter to the owner of the building. The smart card

stores a unique secret key k

enc

sid

used for the encryption

besides other data, as listed in Table 2.

2- A customer fixes a contract with an

: The EP assigns the sid of the customer’s smart

meter to a group G

gid

according to its geographical

location. Subsequently, the EP requests the KA to

add smart meter’s sid to the selected group G

gid

. The

KA knows the secret keys of all smart meters. It adds

the new smart meter’s secret key k

enc

sid

to the set K

enc

gid

which is composed of the secret keys of the smart

meters belonging to the group G

gid

. The KA then

sends a key update to the EP. The key update includes

the gid of the group the meter is added to, the period

j from which on the meter is active, a number of

periods n and a set of n period keys (i.e., periods

j, ..., j + n) used for the additively homomorphic

encryption scheme. Each period key k

enc

gid, j

for a group

gid

and period j is calculated by the KA like:

enc

gid, j

∑

sid∈G

gid

h(k

enc

sid

|| j) mod m

enc

(1)

That is, the KA aggregates the period keys of the indi-

vidual smart meters belonging to the group gid for the

period j. The smart meters’ period keys are derived

from their root keys using a one-way hash function

h() and the period j. Please note that each aggregated

period key k

enc

gid, j

is later used by the EP to decrypt

the encrypted, aggregated sum of metered values of

the group G

gid

reported for period j. Moreover, every

key update includes n period keys for the homomor-

phic MAC mechanism used to check the authenticity

of the aggregated energy measurements. Each MAC

key update k

mac

gid, j

for a group G

gid

and a period j is

calculated by the KA like:

mac

gid, j

∑

sid∈G

gid

F(k

mac

||sid|| j) mod m

mac

(2)

where (sid|| j) corresponds to the i of Table 1. Sub-

sequently, the KA sends the MAC key k

mac

of the EP

to the smart meter, which is used by the smart meter

to authenticate the individual encrypted energy mea-

surements. Additionally, the KA sends the key update

mac

gid, j

to the EP, which is used by the EP to verify the

authenticity of encrypted aggregates. Finally, the EP

adds the freshly received periodical encryption and

MAC keys, associated with the corresponding groups

as described below, to a local key database.

We propose that each EP manages a SQL key

database, storing the periodical keys received from

the KA. As we will show, a SQL key database can eas-

ily calculate the aggregated keys required to decrypt

the aggregated, encrypted consumptions of multiple

groups, according to speciﬁc selective queries. Al-

ternatively to local key databases, the KA could pro-

vide a key database. However, the security require-

ments for a key database at the KA would be very

high and the it should not be publicly accessible to

protect it against certain attacks. Moreover, the scal-

ability of a key database at the KA must be compara-

ble to the scalability of the EMS, because they have

to deal with nearly identical queries and amounts of

data. In contrast, a local key database at an EP must

only store the aggregated period keys of groups asso-

ciated with the EP. We argue that these security and

scalability requirements render a public database for

period keys at the KA unfeasible. Thus, we locate lo-

cal key databases at each service. When receiving the

period keys, an EP executes SQL INSERT statements

to import the keys. Table 3 and 4 show an exemplary

SQL key database managed by the EP.

3- A customer quits a contract with an

: The KA removes the meter’s secret key k

enc

sid

from the set of secret keys K

enc

gid

of the group G

gid

the meter was initially added to. Subsequently, the

KA calculates the set of periodical encryption and

MAC keys anew (as shown in Equation 1 and 2,

respectively) using the keys of the smart meters

remaining in the group G

gid

. The KA then sends the

key update including the freshly computed periodical

SECRYPT2012-InternationalConferenceonSecurityandCryptography

106

Table 3: SQL table keys located at each service, storing the

period keys received from the KA.

enc key mac key group id period

... ... ... ...

977285.. 186928.. 120211 2011-05-10 12:15

517848.. 174516.. 120212 2011-05-10 12:15

703805.. 184878.. 1 2011-05-10 12:30

100833.. 127747.. 2 2011-05-10 12:30

... ... ... ...

Table 4: SQL table groups located at each service, storing a

group’s associated e.g., zip and city.

group id zip city

... ... ...

120210 20357 Hamburg

120211 20357 Hamburg

120212 20358 Hamburg

... ... ...

MAC and encryption keys to the service. When

receiving the key update, the EP again updates its key

database as described in the previous scenario.

4- A smart meter reports its energy

consumption to the EMS

: For example, every 15

minutes, each smart meter reports its energy con-

sumption e

sid, j

to the EMS. Before, e

sid, j

is encrypted

using the encryption function Enc(). Additionally,

a MAC tag for the resulting ciphertext is computed.

The encryption is performed using a period key

derived from the smart meter’s root encryption key

enc

sid

and the period j like

sid, j

= Enc(e

sid, j

,h(k

enc

sid

|| j),m)

= e

sid, j

+ h(k

enc

sid

|| j) mod m

enc

(3)

Once the energy measurement is encrypted, a MAC

tag is computed using the keys (k

mac

) of the EP:

sid, j

= G(k

mac

) · c

sid, j

+ F(k

mac

||sid|| j) mod m

mac

(4)

The size of m

mac

can be set to the output size of the

pseudo-random function. When receiving the con-

sumptions and tags, the EMS inserts them into its con-

sumption database. Table 5 and 6 show the exemplary

consumption database managed by the EMS.

We assume that the connection between a smart

meter and the EMS is reliable. Nevertheless, the EMS

can additionally request missing meter data from a

smart meter. The smart meter then encrypts and

authenticates the missed consumption as described

above. More details on the issue of smart meters be-

ing ofﬂine are discussed in Section 6.2.3.

enc

must be chosen sufﬁciently large to avoid over-

ﬂows. Assume that the largest query that a service can issue

is composed of n ciphertexts. Then, m

enc

must be set to

⌈log

(p·n)⌉

, where p = max(e

) (Castelluccia et al., 2005).

Table 5: SQL table consumptions located at the EMS, stor-

ing encrypted consumptions, their periods and meters.

consumption tag meter id period

... ... ... ...

692169.. 17485.. 5000009 2011-05-10 12:15

629388.. 43894.. 5000001 2011-05-10 12:30

589178.. 43894.. 5000003 2011-05-10 12:30

702046.. 32894.. 5000007 2011-05-10 12:30

... ... ... ...

Table 6: SQL table meters located at the EMS, storing a

meter’s associated e.g., zip and city.

meter id zip city

... ... ...

5000009 20357 Hamburg

5000001 20357 Hamburg

5000003 20358 Hamburg

... ... ...

5- Querying the EMS for aggregated

consumptions

: To retrieve a group’s energy con-

sumption for arbitrary periods, services can send

arbitrary queries to the EMS. To answer the queries,

the EMS uses its database storing the encrypted con-

sumptions like shown in Table 5 and 6. For instance,

to query the EMS for the aggregated consumption

c of meters having a zip preﬁxed by ’20’, the EP

sends the following SQL-query to the EMS: To

SELECT SUM

(c.consumption)

FROM

consumptions c, meters m

WHERE

c.meter_id = m.meter_id

AND

m.zip

'20%'

AND

c.period

BETWEEN

'2011-05-10 12:00'

AND

'2011-05-10 12:30'

verify the authenticity and integrity, an aggregated

MAC tag is computed for the aggregated, encrypted

consumption by querying the EMS: The EP queries

SELECT sum

(c.tag)

FROM

consumptions c, meters m

WHERE

c.meter_id = m.meter_id

AND

m.zip

'20%'

AND

c.period

BETWEEN

'2011-05-10 12:00'

AND

'2011-05-10 12:30'

the key database to verify the tag: The aggregated

SELECT SUM

(k.mac_key)

FROM

keys k, groups p

WHERE

k.group_id = g.group_id

AND

g.zip

'20%'

AND

k.period

BETWEEN

'2011-05-10 12:00'

AND

'2011-05-10 12:30'

MAC tag is valid if Verify(k

mac

,b,c,t) = 1. To

decrypt the sum c received from the EMS, the EP

still has to calculate the aggregated key k by using its

local key database:

HomomorphicPrimitivesforaPrivacy-friendlySmartMeteringArchitecture

107

SELECT SUM

(k.enc_key)

FROM

keys k, groups g

WHERE

k.group_id = g.group_id

AND

g.zip

'20%'

AND

k.period

BETWEEN

'2011-05-10 12:00'

AND

'2011-05-10 12:30'

By using the aggregated key k, the EP can decrypt

the encrypted aggregate c, received from the EMS.

5.3.1 Billing

A temporal grouping scheme can be used to e.g., bill a

customer, as it allows to query aggregated consump-

tions of a single customer while still preserving the

customer’s privacy. To preserve the privacy, the EP

may only be able to decrypt aggregated energy con-

sumptions for a sufﬁciently large period. Neverthe-

less, aggregating consumptions of a single customer

over time is better suited to build customer proﬁles

than it is the case for the spatial grouping scheme. For

instance, if energy prices change frequently,e.g., mul-

tiple times a day, the period lengths are not sufﬁcient.

In contrast, energy prices changing on a monthly ba-

sis only are better suited for the proposed temporal

grouping scheme, even if there are different rates for

the nights and days within a month. For the temporal

grouping scheme to work, the KA has to include these

aggregated keys within each key update. The keys for

the temporal scheme are again derived from the root

keys k

enc

sid

and k

mac

as shown in Section 5.3. How-

ever, the keys must be aggregated by the KA such that

the keys can exclusively be used to verify and decrypt

the aggregated MAC tags and consumptions for the

period speciﬁed in the queries above, i.e. all nights

within a month, to preserve the customers’ privacy.

5.3.2 Multiple Services

Associating a smart meter with multiple services re-

quires the smart meter to use individual encryption

and MAC keys for each service. This is necessary to

mitigate colluding attacks described in Section 6.2.3

and it allows the groups associated with a service to

be individually composed for each service. Let S

sid

denote the set of services a smart meter sid is associ-

ated with. The period keys for each service s ∈ S

sid

are computed by the KA as follows:

enc

s,gid, j

∑

sid∈G

s,gid

h(k

enc

sid

||s|| j) mod m

enc

(5)

mac

s,gid, j

∑

sid∈G

s,gid

F(k

mac

s,2

||sid|| j) mod m

mac

(6)

Smart meters report separate ciphertext-tag pairs to

the EMS for each service they are associated with. A

consumption is encrypted for each service s ∈ S

sid

s,sid, j

= e

sid, j

+ h(k

enc

sid

||s|| j) mod m

enc

(7)

Similarly,the MAC tag for an encryptedmeasurement

is computed for each service s ∈ S

sid

like:

s,sid, j

= G(k

mac

s,1

)·c

s,sid, j

+F(k

mac

s,2

||sid|| j) mod m

mac

(8)

6 SECURITY ANALYSIS

6.1 Trust Model

The following trust model is considered.

Services

- From the consumers’ perspective, the

EP as well as other services are untrusted. Services

want to obtain as much ﬁne-granular consumptions as

possible, thereby threatening the customers’ privacy.

EMS

- We expect the EMS to usually work cor-

rectly such that queries sent to the EMS return a cor-

rect result. Thus, the EMS is functionally trusted.

However, beyond the functional trust, the EMS is

completely untrusted. Query results can be modi-

ﬁed via hardware failures or attacks. We do not trust

the EMS to keep personal data secret. Moreover, the

EMS may be located at a cloud provider. It can be

located in a country other than the services or the GP

where different privacy rules apply. Even if the cloud

provider does not immediately earn any value from

obtaining the customer consumptions, the amount of

stored values may possibly arouse the provider’s in-

terest. Therefore, we argue that an additional level of

protection is necessary to prevent the EMS and cloud

provider from obtaining any unencrypted consump-

tions, neither ﬁne-granular nor aggregated.

- The KA is a trusted third party. The KA is as-

sumed to sufﬁciently protect its services, systems and

keys. The KA gives keys and other data to authorized

parties according to clearly deﬁned contracts only.

- We assume that the GP installs smart meters

which are not compromised and can thus be trusted.

Customers

- The customers are untrusted. Cus-

tomers want to pay as less as possible. Hence, they

would probably manipulate the messages sent or re-

ceived by their meters. However,the customers do not

want anyone to obtain ﬁne-granular consumptions.

Smart Meters

- The smart meters are trusted.

They are assumed to work correctly and to be uncom-

promised. The keys and other sensitive data are as-

sumed to be protected from unauthorized access. Fi-

nally, smart meters are assumed to be protected from

physical attacks via a proper seal.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

108

6.2 Attacks

6.2.1 Breaking the Homomorphic Encryption

Compromising a period key

- The homomorphic

encryption scheme we use allows to trivially deduct

the encryption key from a ciphertext using a known-

plaintext attack. Assume that a message e is en-

crypted under a key k such that c = e + k mod m.

An attacker can obtain the secret encryption key sim-

ply by computing k = c− e mod m if the ciphertext-

plaintext pair (c, e) is known to the attacker. Luckily,

breaking a period key does not imply a total break

where an attacker obtains a root key as the security of

the encryption scheme relies on a keystream changing

from one message to the next. This is the case for our

protocol as each period key h(k

enc

sid

|| j) is derived from

a meter’s root key k

enc

sid

using a one-way hash function

for each period j. The root key is individually chosen

for each meter. Hence, our architecture reveals no in-

formation on the ﬁne-granular and aggregated energy

consumptions as long as the period and aggregated

period encryption keys are unknown to the attacker.

Compromising a root key

- Based on the re-

sults of (Castelluccia et al., 2005), compromising a

smart meter’s root key k

enc

sid

is only possible by com-

promising a meter itself or the KA. As assumed in

Section 6.1, this is not possible.

Decrypting fine-granular consumptions

If any party, except a particular smart meter or KA,

can decrypt ﬁne-granular consumptions, the privacy

of at least one customer is lost. In accordance to Table

5, the EP can always query the EMS for ﬁne-granular

consumptions. However, recall that in this case the

key database, as shown in Table 3, can not be used to

query the aggregated decryption key k. Even if a tem-

poral grouping scheme is used, the KA is not allowed

to reveal keys for such ﬁne-granular periods. Thus,

although c is received, the EP is unable to decrypt c.

6.2.2 Breaking the Homomorphic MAC

Random forgeries

- The attacker wants to manipu-

late either stored or aggregated encrypted values. As

the measurements and their aggregations are authen-

ticated using a homomorphic MAC like shown in Ta-

ble 1, the attacker needs to compute a valid MAC tag

for any value the attacker manipulates. However, as

shown in (Agrawal and Boneh, 2009), the probability

of producing a valid tag without knowing the MAC

key is 1/2

, where q is the size of the tag in bits

(Agrawal and Boneh, 2009) and thus, the probabil-

ity is negligible. We propose 128-bit tags to achieve

a sufﬁcient level of security against adversarial modi-

ﬁcation of energy measurements. Thus, the attacker

cannot alter stored or aggregated encrypted values

without being detected if the MAC key is unknown.

Compromising a MAC key

- Compromising a

MAC key k = (k

) implies breaking the secure

functions G and F which can be implemented using

AES. The attacker needs to deduct the keys k

and k

from the outputs u = AES(k

) and b = AES(k

,i), re-

spectively. However, this requires breaking the secu-

rity of AES which is computationally infeasible with

sufﬁciently large keys (e.g., 128 bits).

6.2.3 Other Attacks

Colluding Attacks

- Multiple parties can share

keys to perform attacks. Malicious cooperations are:

(Service, Service)

- Two services a and b can

cooperate to exchange key updates received from the

KA, such that each service can send more comprehen-

sive queries to the EMS. However, the privacy of cus-

tomers is not at risk, because each service is only able

to decrypt aggregated consumptions of groups. More-

over, as shown in Section 5.3.2, the encryption keys

are individually chosen for each service. This choice

mitigates another attack: As groups can be differently

composed for each service, the services would be able

to calculate sub-group keys if a group G

of service a

is a sub-group of G

of service b while the keys are

not individually chosen for each service, i.e. G

⊂ G

For instance, assume that G

and G

only differ in a

single member. The period keys of this member could

be trivially broken. Our solution, choosing individual

encryption keys for each service, mitigates this attack.

(EMS, Service)

- A service can hand out its pe-

riod decryption keys as well as its individual MAC

key to the EMS. Subsequently, the EMS can decrypt

aggregated consumptions. Still, the privacy of indi-

vidual customers is not at risk. Additionally, the EMS

is subsequently able to calculate valid MAC tags for

the service such that random forgeries of the EMS can

not be detected by the service. However, the damage

of such an attack is limited to the service that shares

its MAC key maliciously with the EMS, as our archi-

tecture assigns unique MAC keys to each service.

DoS Attacks

- If an energy consumption of a me-

ter is missing at the EMS for a period, the stored con-

sumptions of the associated group and speciﬁc period

can still be queried, but the aggregate can no longer be

decrypted correctly. Thus, an attacker can perform a

DoS attack on the smart meters to prevent them from

reporting to the EMS and to subsequently prevent the

decryption of the aggregates. To handle these kinds

of errors, in our architecture the EMS sends an error

message to the querier when energy consumptions of

meters are missing for the queried period. Techniques

increasing robustness must be employed to increase

HomomorphicPrimitivesforaPrivacy-friendlySmartMeteringArchitecture

109

the resilience against such attacks by e.g., using a

dual-sim setup for the smart meters.

Replay Attacks

- Replacing an actual energy

measurement with an already reported one is a sim-

ple way of altering the energy measurements. Our

architecture mitigates such attacks, as energy reports

of smart meters are authenticated with a MAC tag

computed over a unique period number, a smart meter

identiﬁer and a group identiﬁer.

7 PERFORMANCE ANALYSIS

7.1 Performance Overhead

Our evaluation environmentis composed of a MySQL

5.1 server, provided by Debian 6.0.3, running the de-

fault conﬁguration without optimizations. The server

runs on an Intel Core i3 2310-M, 4GB RAM and

a 320GB HDD at 7200rpm. The database stores

the consumptions of the EMS. It is randomly ﬁlled

with encrypted consumptions of 10000 meters for one

month at an interval of 15 minutes such that 30 mil-

lion consumptions and MAC tags are stored. The re-

sults regarding the database performance are listed in

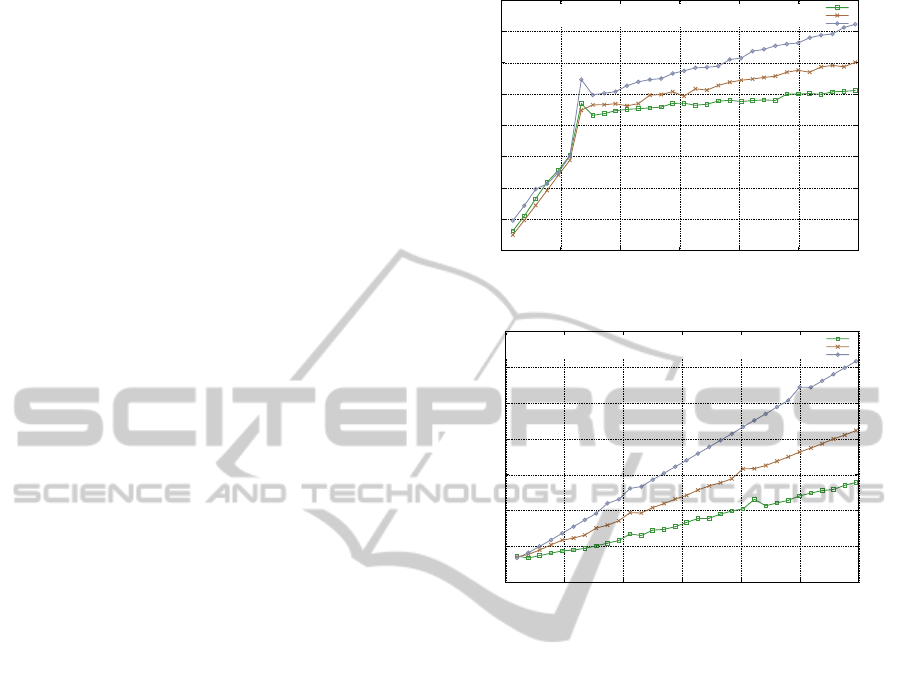
Figure 1. Graph 1) shows response times of queries

on the 16-bit encrypted consumptions. Querying the

sum of 30 million consumptions takes about 10 sec-

onds. Please note that the results shown in graph 1)

are equal to the results of querying a database storing

purely plaintext consumptions, as the plaintext as well

as encrypted consumptions are of equal length. The

response times for queries on the respective MAC tags

are shown in graph 2). Querying the sum of 30 mil-

lion MACtags takes about 12 seconds. As these MAC

tags are 128-bits long, querying the tags continually

takes more time, compared to the response times for

the 16-bit encrypted consumptions. Finally, graph 3)

shows the response times for queries including con-

sumptions as well as MAC tags, such that a single

query returns the aggregated consumption and MAC

tag. The decreasing growth when querying more than

approx. six million consumptions, apparently notable

in Figure 1, is caused by a database speciﬁc optimiza-

tion. MySQL stops using the index on the period,

which is used for selective queries such as:

SELECT SUM

(consumption )

FROM

consumptions

WHERE

period

BETWEEN

'2011-05-01 00:00'

AND

'2011-05-08 00:00'

For larger amounts, MySQL decides not using the

index to be cheaper. However, in real-world settings

the index usually will be used, because much more

0 5e+06 1e+07 1.5e+07 2e+07 2.5e+07 3e+07

Response time [Sec]

Amount of queried consumption measurements and MAC tags

1) 16-bit encrypted consumptions (EMS)

2) 128-bit MAC tags (EMS)

3) 16-bit encrypted consumptions and 128-bit MAC tags (EMS)

Figure 1: Response times when querying the EMS.

1.2

1.4

1.6

1.8

2.2

2.4

0 1e+06 2e+06 3e+06 4e+06 5e+06 6e+06

Response time [Sec]

Amount of queried keys (five meters per group)

1) 16-bit decryption keys (local key database)

2) 128-bit MAC keys (local key database)

3) 16-bit decryption keys and 128-bit MAC keys (local key database)

Figure 2: Response times when querying a local key

database for aggregated decryption and MAC keys.

consumptions will be stored compared to our evalu-

ation. Please note that this issue is independent of

our architecture, because MySQL will make the same

decisions for databases storing purely plaintext con-

sumptions.

To verify and decrypt the responses of the EMS,

the querying service must additionally query a sec-

ond database, the local key database, for the aggre-

gated decryption key as well as for the aggregated

MAC key. In our setup, the smart meters are spa-

tially organized in 2000 groups such that each group

is composed of ﬁve smart meters. Thus, six million

encryption keys as well as MAC keys are required to

validate and decrypt the responses to all selective ag-

gregation queries possible on the 30 million consump-

tions stored within the database of the EMS. More-

over, the response times of these queries are shown in

Figure 2, which correspondingly are about ﬁve times

lower than the response times shown in Figure 1.

7.2 Storage Requirements

Architectures without privacy protection would sim-

ply store 16-bit plaintext consumptions at the EMS.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

110

Contrary, our privacy-friendly architecture stores en-

crypted 16-bit consumptions each with a 128-bit

MAC tag at the EMS. Thus, the storage requirements

of our architecture grow linearly with the number of

stored consumptions. Storing 100 million consump-

tions with their MAC tags requires 1.8 GB of stor-

age in contrast to 200 MB required to simply store

plaintext consumptions. Besides the overhead for the

EMS, each service must store the group-wise aggre-

gated keys sent by the KA, required to verify and de-

crypt the responses to queries directed to the EMS. If

a spatial grouping scheme is used while each group is

composed of ﬁve smart meters, the overhead of stor-

ing the keys required to decrypt all possible aggre-

gates composed of 100 million consumptions is about

343 MB for each service. Contrary, the KA must not

store any period keys. It must only store the private

symmetric key k

enc

sid

as well as the private-public key

pair (k

priv

sid

pub

sid

) of each smart meter sid, such that the

storage requirements of the KA are equal to the num-

ber of smart meters multiplied with a constant factor

which corresponds to the key lengths. Thus, the stor-

age requirements of the KA are negligible.

8 CONCLUSIONS

This work presents a smart metering architecture

which is ﬂexible enough to serve various services

while still preserving the customers’ privacy. Privacy

is preserved using a database storing purely encrypted

energy consumptions and a policy forcing a strict but

ﬂexible grouping, like temporal and spatial grouping

of the smart meters. The database may be located in a

mutual suspicious cloud environment without affect-

ing our privacy guarantees. Third-party services, like

energy providers, can aggregate the encrypted con-

sumptions at the database level using various selec-

tive SQL queries. The responses to these queries can

only be successfully decrypted if the queries are valid

according to the grouping scheme and privacy poli-

cies enforced by a key authority. Thus, our protocol

requires a trusted third party. However, it is rarely in-

volved, as its primary task is to hand out sets of secret

encryption keys to the smart meters that can be used

for a long time. Finally, our privacy-friendly architec-

ture, while ﬂexible, imposes only a moderate perfor-

mance and storage overhead.

ACKNOWLEDGMENTS

The work presented in this paper was partly supported

by the German BMWi SmartPowerHamburg project.

The views and conclusions contained herein are those

of the authors and should not be interpreted as nec-

essarily representing the ofﬁcial policies or endorse-

ments, either expressed or implied of the SmartPow-

erHamburg project.

REFERENCES

Agrawal, R., Kiernan, J., Srikant, R., and Xu, Y. (2004). Or-

der preserving encryption for numeric data. SIGMOD

’04. ACM.

Agrawal, S. and Boneh, D. (2009). Homomorphic MACs:

MAC-Based Integrity for Network Coding. ACNS

’09. Springer.

Ben-Or, M., Goldwasser, S., and Wigderson, A. (1988).

Completeness theorems for non-cryptographic fault-

tolerant distributed computation. STOC ’88. ACM.

Bohli, J.-M., Sorge, C., and Ugus, O. (2010). A privacy

model for smart metering. ICC ’10. IEEE.

Castelluccia, C., Mykletun, E., and Tsudik, G. (2005). Efﬁ-

cient aggregation of encrypted data in wireless sensor

networks. MobiQuitous ’05.

Chaum, D., Cr´epeau, C., and Damgard, I. (1988). Mul-

tiparty unconditionally secure protocols. STOC ’88.

ACM.

Domingo-Ferrer, J. (2002). A provably secure additive

and multiplicative privacy homomorphism. ISC ’02.

Springer.

Efthymiou, C. and Kalogridis, G. (2010). Smart grid

privacy via anonymization of smart metering data.

SmartGridComm ’10. IEEE.

Enev, M., Gupta, S., Kohno, T., and Patel, S. N. (2011).

Televisions, video privacy, and powerline electromag-

netic interference. CCS ’11. ACM.

EnWG (2005). Energiewirtschaftsgesetz, Germany. BGBl I

2005, 1970. Geaendert durch Art. 8 G v. 2011 I 1634.

Federal Ofﬁce for Information Security (2011). Protection

proﬁle for the gateway of a smart metering system.

Garcia, F. D. and Jacobs, B. (2010). Privacy-friendly

energy-metering via homomorphic encryption. Lec-

ture Notes in Computer Science, V. 6710. Springer.

Johnson, R., Molnar, D., Song, D. X., and Wagner, D.

(2002). Homomorphic signature schemes. CT-RSA

’02. Springer.

Kursawe, K., Danezis, G., and Kohlweiss, M. (2011).

Privacy-friendly aggregation for the smart-grid. Lec-

ture Notes in Computer Science, V. 6794. Springer.

Li, F., Luo, B., and Liu, P. (2010). Secure information ag-

gregation for smart grids using homomorphic encryp-

tion. IEEE.

McLaughlin, S., McDaniel, P., and Aiello, W. (2011). Pro-

tecting consumer privacy from electric load monitor-

ing. CCS ’11. ACM.

Mykletun, E., Girao, J., and Westhoff, D. (2006). Public key

based cryptoschemes for data concealment in wireless

sensor networks. ICC ’06. IEEE.

HomomorphicPrimitivesforaPrivacy-friendlySmartMeteringArchitecture

111

NIST11 (2010). NIST Interagency Report 7628: Guidelines

for Smart Grid Cyber Security: Vol. 2, Privacy and the

Smart Grid.

Peter, S., Piotrowski, K., and Langendoerfer, P. (2007). On

Concealed Data Aggregation for Wireless Sensor Net-

works. CCNC ’07. IEEE.

Rial, A. and Danezis, G. (2011). Privacy-preserving smart

metering. WPES ’11. ACM.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

112