
Ontology Similarity Measurement Method in Rapid Data Integration
Juebo Wu, Chen-Chieh Feng and Chih-Yuan Chen
Department of Geography, National University of Singapore, 1 Arts Link, Singapore 117570, Singapore
Keywords: Ontology Similarity, Rapid Data Integration, Ontology Mapping.
Abstract: Rapid data integration has been a challenging topic in the field of computer science and its related subjects,
widely used in data warehouse, artificial intelligence, biological medicine, and geographical information
system etc. In this paper, we present a method of ontology similarity measurement in rapid data integration,
by means of semantic ontology from high level perspective. The edit distance algorithm is introduced as the
basic principle for ontology similarity calculation. A case study is carried out and the result shows that the
presented method is feasible and effective.
1 INTRODUCTION
In the study of data integration, it is a very important
branch to focus on rapid, automatic and high
efficient methodologies of data sharing in
enterprises, data interaction in projects and data
communication in team cooperation, which we
regard it as rapid data integration. In recent decades,
great progress has been achieved for data integration
and data sharing. The methods for data integration
can be mainly divided into two aspects, by schema
matching or by ontology mapping. For schema
matching, Madhavan, Bernstein and Rahm (2001)
presented an algorithm for generic schema matching
without depending on a specific data framework or
application. Do and Rahm (2002) designed the
COMA schema matching system to integrate a
number of matchers. Rahm and Bernstein (2001)
gave a survey of approaches to automatic schema
matching. For ontology mapping, Ceravolo,
Damiani, Gusmini and Leida (2007) presented a data
integration system named Global Representation,
which can handle a variety of relations existing
between concepts of ontologies. Souza, Belian,
Salgado and Tedesco (2008) proposed a context
ontology to formally represent context in data
integration process (CODI) by using ontology
reasoning. Godugula and Engels (2008) performed a
survey of ontology-based approaches.
Despite these research efforts, most contributions
are related to particular fields, and substantially
based on the bottom level of data such as raw data.
They consider less on using the upper semantic and
ontology knowledge. Moreover, under the
circumstance of rapid data integration, most of
presented methods are difficult to extend to other
domains and hard to be achieved quickly and
efficiently. To overcome these problems, this paper
presents a new approach for ontology similarity
measurement in rapid data integration, which can be
used for data communication from diverse systems.
2 OUR APPROACH
In order to realize rapid data integration, the most
important thing is that both participants can
understand the data structures well for each other.
To fulfill such demands, our idea is as below: At the
beginning, we construct the ontology relationship
between data table and semantic ontology, such as
table to class, record to individual and so on. After
that, we carry out ontology similarity calculation for
different parties and the ontology relationship can be
obtained. Though ontology relationship, the same
contents can be integrated.
For mapping raw data to semantic data, we
define ontology based on OWL DL and product
them by data transformation. For ontology similarity,
we compute similarity between two ontologies by
considering comprehensive similarities of multiple
features of ontology. Each character of ontology is
selected to compute its similarity with other
ontology, and this process can be simplified to
compare the similarity with their minimum feature
names, that is, the similarity between two words.
237
Wu J., Feng C. and Chen C..
Ontology Similarity Measurement Method in Rapid Data Integration.
DOI: 10.5220/0004037102370240
In Proceedings of the International Conference on Data Technologies and Applications (DATA-2012), pages 237-240
ISBN: 978-989-8565-18-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Edit distance (Levenshtein, 1966) is adopted here
because it is a good manner to calculate the
similarity for two words with high efficiency.
3 ONTOLOGY SIMILARITY
The goal of ontology similarity measurement is to
find out a pair of two ontologies’ concepts which
have the same meaning but described in different
ways. Here, we put forward a novel approach to get
the similarity between ontologies based on edit
distance.
3.1 Ontology Extraction
Ontology extraction is the first step in rapid data
integration, which generates ontology from different
databases and distributed network nodes. The
ontology extraction methods and steps are given as
follows.
(1) Class and subclass construction.
Class is an important element in ontology
construction. In accordance with the storage
characteristics of database, one class will be
generated from one data table. The class name of the
table is directly transferred to the class name.
Consider a data table structure. If existing a
subclass, it must emerge that one field is referred to
the primary key as its foreign key in the form of the
data table. Thus, the corresponding subclass will be
generated when the data table exists such condition.
For example, the field Table1_id as primary key is
the foreign key of the field column1 in Table1. If
there exists a record that column1 with value
column1_value and Table1_id with Table1_id_value,
then a subclass should be created as
Table1_id_value is the subclass of column1_value.
And the class names are respectively
Table1_id_value and column1_value.
In addition, the platform provides the way
through user defined, achieving the goal of
contenting to different demands for subclass
construction. For example, in the data table Table1
(column1, column2, column3, column4), the main
class Table1 has been generated before, then we can
carry out partition for certain field. If the user
divides the column3 into low, medium and high,
then the table can generate three different subclasses
Table1.low, Table1.medium, the Table1.High.
(2) Property construction.
Object property: If a field in a table (T1) depends
on second table (T2), an object property of the class
corresponding to T2 should be created. The
property’s range and domain should be also created
according to dependencies of such object properties.
For datatype property, it can be created from the
fields’ types. The process of datatype property can
be combined with the construction for individual
construction.
Sub-property is the supplement for property
construction. Since sub-property cannot be produced
directly from data table, two ways are provided to
create sub-properties: 1) manually define sub-
properties and 2) automatically extract property
hierarchy from user-defined property tables. The
former one is that the user can form sub-properties
by selecting one property as the sub-property of the
other’s. And the latter one can generate sub-
properties according the rules described in user-
defined property tables.
(3) Individual construction.
Each record in the data table corresponds to one
individual in ontology construction. Generally, it is
feasible to conduct ontology mapping by generate
the corresponding individuals for all records in the
table.
(4) Domain and Range.
The domain and the range of datatype property
are corresponding to data types of the fields in the
data table. If the field refers to other data table, the
range of this property is regarded as object property.
(5) Other construction.
In order to improve the accuracy of ontology
mapping, some aid information is also added into
computing process, such as complex class, property
feature and property restriction.
3.2 Similarity Calculation
Since several aspects for data sources should be
considered in rapid data integration such as table
name, column name etc., and the existing ontology
concept similarity algorithm can't meet the
integrated requirements. In order to solve this
problem, multiple features of one ontology are
involved into calculation, that is, several similarities
are calculated for one ontology when doing ontology
similarity analysis.
(1) Similarity between classes or subclasses.
23
11
1
//
(1 )( )
2
od
nn
opdp
ii
nSsum nSsum
CSi S
ββ
==
×+×
=× +−
∑∑
(1)
where
2
)(/
maxmin
1
ij
SCNDD
S
+
=
,
2
)(
2
ijoc
SOCNS
S
+
=
and
)(
3 ij
SDCNS
=
.
DATA2012-InternationalConferenceonDataTechnologiesandApplications
238
In equation (1),
β
is a weighting parameter
between 0 and 1, and sum
p
is the number of
properties while n
o
and n
d
stand for the number of
object property and data property respectively. In S
1
,
min
D
and
max
D
are the minimum and maximum of the
out-degree in a class diagram and
)(
ij
SCN
denotes
the similarity of the related class names calculated
by the edit distance. In S
2
,
oc
S
is the similarity of the
corresponding domain class of object property, and
)(
ij
SOCN
is the similarity of the edit distance of
object property name. S
3
is the similarity of the edit
distance of data property name. The pre-defined
parameter
β
adjusts for different data integration
requirements to improve matching accuracy.
(2) Similarity of properties.
For data property:
2
)(
ijdc
SDCNS
DSi
+
=
(2)
where
dc
S
is the similarity of data property domain
class.
)(
ij
SDCN
is the similarity of the data property
name.
For object property:
3
)(
ijocdc
SRCNSS
OSi
+
+
=
(3)
where
dc
S
is the similarity of domain class and
oc
S
is
the similarity of range class.
)(
ij
SRCN
is the
similarity of the data property name.
(3) Similarity of individual.
)
2
//
(
11
21
∑∑
==
×+×
×=
od
n
i
n
i
pdpo
sumSnsumSn
CSiISi
(4)
where
2
)(
1
ij
SICNCSi
S
+
=
and
)(
2 ij
SICNS =
.
In equation (4),
CSi
is the similarity of class, and
sum
p
is the number of properties while n
o
and n
d
stand for the number of object property and data
property respectively. In
1
S
and
2
S
,
CSi
is the same
as equation (4) and
)(
ij
SICN
is the similarity of
individual.
(4) Domain, range, and others.
The similarities of rest of the elements can be
computed directly using the edit distance. Through
the equations above, a similarity value can be
obtained between 0 and 1 for any two classes, two
properties, and two individuals. Ontology mapping
can be established between two computing objects
by selecting the bigger value. In order to improve
the accuracy, the platform often provides the
interface to users for modification of results in real
applications. According to the presented algorithm,
we can see that the similarity between concepts
takes many characters into consideration. Therefore,
the similarity of ontology described in different
languages can be also generated, such as between
Chinese and English.
4 CASE STUDY
Team A and team B are two parts in a geographical
project, and they have various research directions
with mutual independence. Team A and team B have
established some systems respectively, which
designed and implemented by different researchers.
Although the function and design of these two
systems are different, parts of the objective data are
the same and all the two systems have stored such
data. System A (developed by team A) can carry out
spatial clustering while system B (developed by
team B) can perform data normalization. Now,
system A wants to cooperate with system B. System
A carries out spatial clustering for the normalized
data which come from system B. The goal is to
achieve rapid data integration by the presented
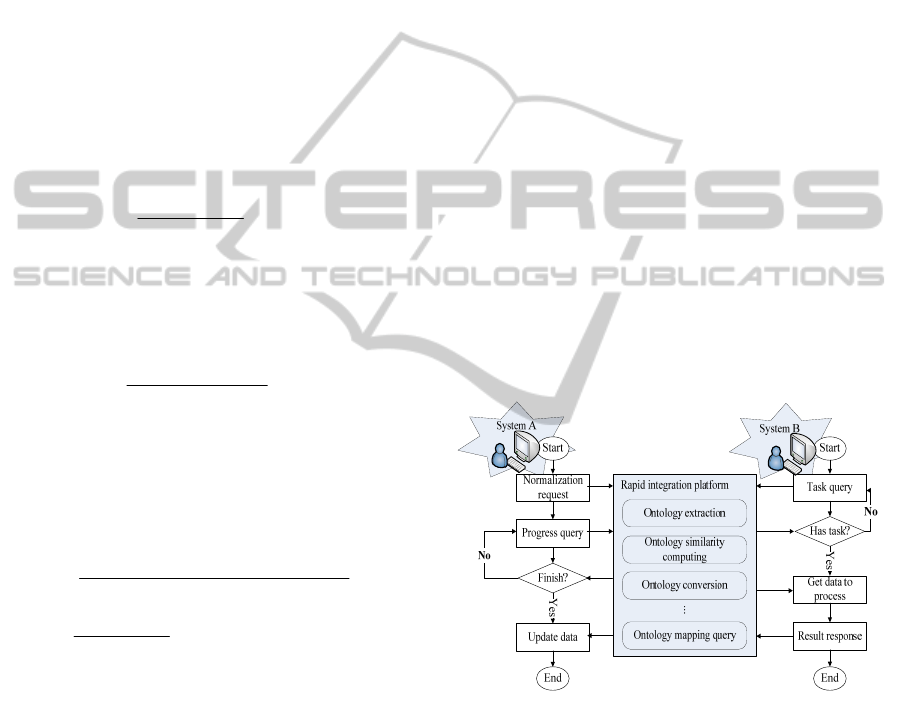
approach and the main steps are shown in Figure 1.
Figure 1: Cooperation process of system A and system B.
4.1 Ontology Extraction
The data structures in system A and system B are
shown in Figure 2, where we can see that not only
the table names are different, but also the column
names are different. The data records in system A
and system B are from the same data source, and
parts of contents in two systems are same while the
rest are not.
From these two tables, two classes are created as
ontology. The individuals of such classes are
generated by the number of data records. The
OntologySimilarityMeasurementMethodinRapidDataIntegration
239

number of properties is decided by the amount of the
fields in two data tables.
Figure 2: Key fields from data table in system A and
system B.
4.2 Ontology Calculation
In this step, the goal is to find out the relationship
between the records from system A and system B
extracted by ontologies.
By using the presented algorithms, the
similarities generated from this task are calculated.
Two classes are created respectively from system A
(i.e., cyclone) and system B (i.e., whirlwind).
Because the column ref_data in cyclone table is
referred to column temp_id, a subclass is generated
for class temp_id is the parent of class ref_data. The
individuals are created according to the task records
with on record for one individual. The fields that
don’t refer to other tables are converted to property
‘dataproperty’, while others with reference to other
tables are converted to property ‘objectproperty’.
4.3 Results Analysis
The accuracy of the results in this system depends
on ontology mapping. In order to improve the
accuracy, a manual interface is provided for the user
to correct when the operation is performing at first
time. Different types of data tables and different
number of fields in data tables are used in this case
study to carry out experiments. Through the
experimental results, it shows that the average
accuracy is 93.77% when using the presented
algorithm to compute ontology similarity. In
traditional data integration among projects or teams,
they need to redefine the data structure. In terms of
the presented method in this paper, the joint systems
can send their data to integration platform without
establishing a new data structure or updating their
existing systems. These make data integration with
rapid speed and more scalability.
5 CONCLUSIONS
For the fields in rapid data integration, this paper put
forward a new approach of ontology similarity
measurement in rapid data integration. The
automatic method for ontology extraction was
presented according to the relationship between data
table and ontology concept. On the basis of ontology
extraction, we can perform ontology similarity
calculation in order to achieve rapid data integration.
A case study was conducted and it can be seen from
the results that the presented method is feasible and
effective.
For future study, we will focus on how to
introduce the presented method into a complete
architecture for rapid data integration in combination
with other technologies such as web service.
ACKNOWLEDGEMENTS
The research described in this project was funded in
whole or in part by the Singapore National Research
Foundation (NRF) through the Singapore-MIT
Alliance for Research and Technology (SMART)
Center for Environmental Sensing and Modeling
(CENSAM).
REFERENCES
Ceravolo, P., Damiani, E., Gusmini, A. and Leida, M.
(2007). Using Ontologies to Map Concept Relations in
a Data Integration System,
OTM 2007 Workshops,
Lecture Notes in Computer Science
, 1285-1293.
Do, H. and Rahm, E. (2002). COMA-A System for
Flexible Combination of Schema Matching
Approaches.
In Proceedings of the VLDB, 610-621.
Godugula, S. and Engels, G. (2008). Survey of Ontology
Mapping Techniques. cs.uni-paderborn.de.
Levenshtein, V. L. (1966). Binary codes capable of
correcting deletions, insertions and reversals. Doklady
Akademii Nauk SSSR
, 163(4), 707-710.
Madhavan, J., Bernstein, P. A. and Rahm, E. (2001).
Generic Schema Matching with Cupid.
Proceeding
VLDB '01 Proceedings of the 27th International
Conference on Very Large Data Bases
.
Rahm, E. and Bernstein, P. (2001). A survey of
approaches to automatic schema matching.
In The
VLDB Journal
, 10(4), 334-350.
Souza, D., Belian, R., Salgado, A. C. and Tedesco, P. A.
(2008).
Towards a Context Ontology to Enhance Data
Integration Processes
. ODBIS 2008, 49-56.
DATA2012-InternationalConferenceonDataTechnologiesandApplications
240
