Effective Keyword Search via RDF Annotations
Roberto De Virgilio and Lorenzo Dolfi
Dipartimento di Informatica e Automazione, Universit
`
a Roma Tre, Rome, Italy
Keywords:
Visualization of Semantic Applications, Semantic Annotation, Web Browsing, Centrality Indices.
Abstract:
Searching relevant information from Web may be a very tedious task. If people cannot navigate through the
Web site, they will quickly leave. Thus, designing effective navigation strategies on Web sites is crucial. In
this paper we provide and implement centrality indices to guide the user for an effective navigation of Web
pages. We get inspiration from well-know location family problems to compute the center of a graph: a joint
use of such indices guarantees the automatic selection of the best starting point. To validate our approach,
we have developed a system that implements the techniques described in this paper on top of an engine for
keyword-based search over RDF data. Such system exploits an interactive front-end to support the user in the
visualization of both annotations and corresponding Web pages. Experiments over widely used benchmarks
have shown very good results, in terms of both effectiveness and efficiency.
1 INTRODUCTION
The original perception of the Web by the vast ma-
jority of its early users was as a static repository of
unstructured data. This was reasonable for browsing
small sets of information by humans, but this static
model now breaks down as programs attempt to dy-
namically generate information, and as human brows-
ing is increasingly assisted by intelligent agent pro-
grams. With the size and availability of data con-
stantly increasing, a fundamental problem lies in the
difficulty users face to find and retrieve the informa-
tion they are interested in (Li et al., 2001). A rele-
vant problem is that using a search engine probably
the retrieved pages are not always what user is look-
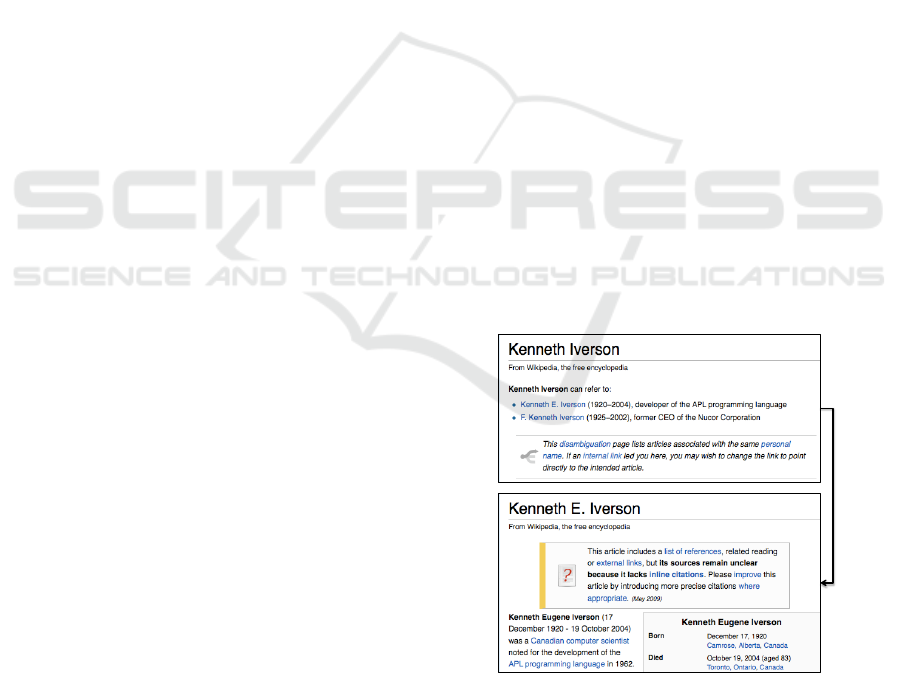
ing for. To give an example, let us consider Wikipedia
and type “Kenneth Iverson APL”, i.e. we would re-
trieve information about the developer of APL pro-
gramming language. As shown Figure 1, the user
has to browse the list of all Kenneth Iverson, then
manually to solve the disambiguation (i.e. selecting
Kenneth E. Iverson) and finally to consume the infor-
mation about development of APL programming lan-
guage following the link in the Web page. Such task is
time consuming and in case of a long chain of links to
follow it could convince the user to quickly leave the
Web site. To this aim “Semantic Web” lies in encod-
ing properties of and relationships between objects
represented by information stored on the Web (De
Virgilio et al., 2010). It envisions that authors of pages
Figure 1: Searching K.E. Iverson, developer of the APL
programming language.
include semantic information along with human-
readable Web content, perhaps with some machine as-
sistance in the encoding. Referring to the example of
Figure 1, we could annotate the corresponding Web
pages with the following RDF triples
<rdf:Description rdf:about="wiki:Kenneth_Iverson">
<rdf:type rdf:resource="wiki:Article"/>
<wiki:redirectsTo rdf:resource="wiki:Kenneth_E._Iverson"/>
<wiki:redirectsTo rdf:resource="wiki:F._Kenneth_Iverson"/>
...
</rdf:Description>
<rdf:Description rdf:about="wiki:Kenneth_E._Iverson">
<rdf:type rdf:resource="wiki:Article"/>
216
De Virgilio R. and Dolfi L..
Effective Keyword Search via RDF Annotations.
DOI: 10.5220/0004037202160222
In Proceedings of the International Conference on Data Technologies and Applications (DATA-2012), pages 216-222
ISBN: 978-989-8565-18-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

K_I!
GPL! A!
MIMD!
F_K_I!
K_E_I!
I_b!
APL!
I_A!
Figure 2: Semantic annotation of K. Iverson pages.
<wiki:internalLink
rdf:resource="wiki:APL_programming_language"/>
<wiki:internalLink rdf:resource="wiki:Iverson_Award"/>
<wiki:internalLink rdf:resource="wiki:Iverson_bracket"/>
...
</rdf:Description>
Due to the huge amount of RDF data available on
the Web (currently around 7 billion RDF triples and
150 million RDF links), keywords search based sys-
tems, e.g. (Cappellari et al., 2011), are increasingly
capturing the attention of researchers, implement-
ing IR strategies on top of traditional database man-
agement systems with the goal of freeing the users
from having to know data organization and query lan-
guages. The aim of such approaches is to query se-
mantic annotations instead of making a deep analysis
of a large number of Web pages. The result is a set
of RDF subgraphs linked to the Web pages of inter-
est. For instance Figure 2 shows the RDF subgraph
matching the query “Kenneth Iverson APL”. For the
sake of simplicity, we used only initials of URIs and
marked matching nodes in gray. However most of the
proposals do not analyze in deep how to exploit the re-
sulting RDF annotation to navigate the pages of inter-
est. The user manually has to analyze the RDF graph,
selecting the starting node from which begins the nav-
igation of the corresponding Web pages. Of course, in
this situation semi-automatic tools would support the
analysis but the risk is to guide the user to select a
wrong starting point, so far from the most interesting
Web pages. For instance looking at the RDF graph
of Figure 2, a semi-automatic tool could select K I as
starting point (i.e. it is the source of the graph): in
this case we reconduct the user to the same situation
of Figure 1. The best choice would be K E I linking
to the Web page of Kenneth E. Iverson.
In this paper we provide and implement centrality
indices to guide the user for an effective navigation
of Web pages. We get inspiration from well-know
location family problems to compute the center of a
graph: a joint use of such indices guarantees the au-
tomatic selection of the best starting point. To vali-
date our approach, we have developed a system that
implements the techniques described in this paper on
top of an engine for keyword-based search over RDF
data. Such system exploits an interactive front-end
to support the user in the visualization of both anno-
tations and corresponding Web pages. Experiments
over widely used benchmarks have shown very good
results, in terms of both effectiveness and efficiency.
The rest of the paper is organized as follows. In Sec-
tion 2 we discuss the related research. In Section 3
we present our centrality indices. Finally Section 4
illustrates the experimental results, and in Section 5,
we draw our conclusions and sketch future works.
2 RELATED WORK
Facility location analysis deals with the problem of
finding optimal locations for one or more facilities in
a given environment. Location problems are classical
optimization problems with many applications in in-
dustry and economy. The spatial location of facilities
often take place in the context of a given transporta-
tion, communication, or transmission system, which
may be represented as a network for analytic pur-
poses. A first paradigm for location based on the min-
imization of transportation costs was introduced by
Weber in 1909. However, a significant progress was
not made before 1960 when facility location emerged
as a research field. There exist several ways to clas-
sify location problems. According to Hakami (Her-
lihy, 1964) who considered two families of location
problems we categorize them with respect to their ob
jective function. The first family consists of those
problems that use a minimax criterion. As an ex-
ample, consider the problem of determining the loca-
tion for an emergency facility such as a hospital. The
main objective of such an emergency facility location
problem is to find a site that minimizes the maximum
response time between the facility and the site of a
possible emergency. The second family of location
problems considered by Hakimi optimizes a minisum
criterion which is used in determining the location for
a service facility like a shopping mall. The aim here
is to minimize the total travel time. A third family
of location problems described for example in (Smart
and Slater, 1999) deals with the location of commer-
cial facilities which operate in a competitive environ-
ment. The goal of a competitive location problem is
to estimate the market share captured by each com-
peting facility in order to optimize its location. Our
focus here is not to treat all facility location prob-
lems. The interested reader is referred to a bibliogra-
phy devoted to facility location analysis (Domschke
EffectiveKeywordSearchviaRDFAnnotations
217

and Drexl, 1985). The aim of this paper is to intro-
duce three important vertex centralities by examining
location problems. Then we can introduce a fourth
index based not only on “spatial” properties (such as
the other centrality indices) but also on the semantics.
The definition of different objectives leads to differ-
ent centrality measures. A common feature, however,
is that each objective function depends on the dis-
tance between the vertices of a graph. In the follow-
ing we focus on G as connected directed graph with
at least two vertices and we suppose that the distance
d(u, v) between two vertices u and v is defined as the
length of the shortest path from u to v. These assump-
tions ensure that the following centrality indices are
well defined. Moreover, for reasons of simplicity we
consider G to be an unweighted graph, i.e., all edge
weights are equal to one. Of course, all indices pre-
sented here can equally well be applied to weighted
graphs.
3 WEB NAVIGATION
As said in the Introduction, the user is supported by
different approximate query processing methods to
improve the search of information on the Web. In par-
ticular Semantic Web was introduced to annotate the
semantic involved into a Web page, making more au-
tomatic the interoperability between applications and
machines and improving the effectiveness of the re-
sults. However a significant issue is to exploit the
result (annotation) of the query processing to navi-
gate the corresponding Web pages in an effective way.
Then, centrality indices can be computed to quantify
an intuitive feeling that in the result some vertices or
edges are more central than others. Such indices can
support the user to navigate directly the part of the
result that best fits the query provided by the user.
3.1 Center Indices
In the following we get inspiration from well-know
location family problems to compute the center of G.
Eccentricity. The aim of the first problem family is
to determine a location that minimizes the maximum
distance to any other location in the network. Suppose
that a hospital is located at a vertex u ∈ V . We denote
the maximum distance from u to a random vertex v
in the network, representing a possible incident, as
the eccentricity e(u) of u, where e(u) = max{d(u, v) :
v ∈ V }. The problem of finding an optimal location
can be solved by determining the minimum over all
e(u) with u ∈ V . In graph theory, the set of vertices
with minimal eccentricity is denoted as the center of
G. Hage and Harary (Harary and Hage, 1995) pro-
posed a centrality measure based on the eccentricity
c
E
(u) =
1
e(u)
=
1
max{d(u, v) : v ∈ V }
This measure is consistent with the general notion
of vertex centrality, since e(u)
−1
grows if the maximal
distance of u decreases. Thus, for all vertices u ∈ V of
the center of G: c(u) > c
E
(v) for all v ∈ V . Based on
such method, we define a procedure to compute the
center of the graph as described in the Algorithm 1.
Algorithm 1: Center computation by eccentric-
ity.
Input : The graph G
Output: The center c
E
1 n ← V.length;
2 L
E
← InitializeArray(n);
3 M ← FloydWarshall(G);
4 for i ← 0 to n do
5 L
E
[i] ← Max(M[i]);
6 i
min
← MinIndex(L
E
);
7 c
E
← V [i
min
];
8 return c
E
;
In the algorithm, by using the function
InitializeArray, we initialize the eccentricity
vector L
E
(line[2]). Such vector has length n (the
number of nodes in V ): for each node with index i
we calculate the maximum distance from the nodes
of G (lines[4-5]). The distances from each couple of
nodes are computed in a matrix M (line[3]) by using
the Floyd-Warshall algorithm (Rosen, 2003), that is
a graph analysis algorithm for finding shortest paths
in a weighted graph. If there does not exist a path
between two nodes we set the distance to ∞. Finally
we select the index i
min
in L
E
corresponding to the
minimum value (line[6]). The center c
E
corresponds
to the node with the index i
min
in V. Referring to the
graph of Figure 2, we have the following matrix
M =
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
∞ 0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
∞ ∞ 0 ∞ ∞ ∞ ∞ ∞ ∞
1 1 1 0 1 1 2 2 2
∞ ∞ ∞ ∞ 0 ∞ ∞ ∞ ∞
∞ ∞ 1 ∞ ∞ 0 1 1 1
∞ ∞ 2 ∞ ∞ 1 0 2 1
∞ ∞ ∞ ∞ ∞ ∞ ∞ 0 ∞
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ 0
where idx(GPL) = 1, idx(MIMD) = 2,
idx(A) = 3, idx(K I) = 4, idx(F K I) = 5,
idx(K E I) = 6, idx(APL) = 7, idx(I b) = 8 and
idx(I A) = 9. Then the eccentricity vector is
L
E
=
∞ ∞ ∞ 2 ∞ ∞ ∞ ∞ ∞
t
. In
DATA2012-InternationalConferenceonDataTechnologiesandApplications
218

L
E
the minimum value is 2, corresponding to the
index 4: in this case the center c
E
is K I.
Closeness. Next we consider the second type of lo-
cation problems - the minisum location problem, of-
ten also called the median problem or service facility
location problem. Suppose we want to place a ser-
vice facility, e.g., a shopping mall, such that the to-
tal distance to all customers in the region is minimal.
This would make traveling to the mall as convenient
as possible for most customers. We denote the sum
of the distances from a vertex u ∈ V to any other ver-
tex in a graph G as the total distance
∑
v∈V
d(u, v).
The problem of finding an appropriate location can be
solved by computing the set of vertices with minimum
total distance. In social network analysis a centrality
index based on this concept is called closeness. The
focus lies here, for example, on measuring the close-
ness of a person to all other people in the network.
People with a small total distance are considered as
more important as those with a high total distance.
Various closeness-based measures have been devel-
oped, see for example (Bavelas, 1950; Beauchamp,
1965; Moxley and Moxley, 1974; Sabidussi, 1966)
and (Valente and Foreman, 1998). The most com-
monly employed definition of closeness is the recip-
rocal of the total distance
c
C
(u) =
1
∑
v∈V
d(u, v)
In our sense this definition is a vertex centrality, since
c
C
(u) grows with decreasing total distance of u and
it is clearly a structural index. Before we discuss
the competitive location problem, we want to men-
tion the radiality measure and integration measure
proposed by Valente and Foreman (Valente and Fore-
man, 1998). These measures can also be viewed as
closeness-based indices. They were developed for di-
graphs but an undirected version is applicable to undi-
rected connected graphs, too. This variant is
c
R
(u) =
∑
v∈V
(4
G
+ 1 − d(u, v))
n − 1
where 4
G
and n denote the diameter of the graph and
the number of vertices, respectively. The index mea-
sures how well a vertex is integrated in a network. The
better a vertex is integrated the closer the vertex must
be to other vertices. The primary difference between
c
C
and c
R
is that c
R
reverses the distances to get a
closeness-based measure and then averages these val-
ues for each vertex.
Based on such method, we define a procedure to
compute the center of the graph as described in the
Algorithm 2. As for the eccentricity, we initialize the
closeness vector L
C
and calculate the matrix M. Then
for each node with index i we calculate the sum of
Algorithm 2: Center computation by closeness.
Input : The graph G
Output: The center c
C
1 n ← V.length;
2 L
C
← InitializeArray(n);
3 M ← FloydWarshall(G);
4 for i ← 0 to n do
5 L
C
[i] ←
∑
n−1
j=0
M[i][ j];
6 i
min
← MinIndex(L
C
);
7 c
C
← V [i
min
];
8 return c
C
;
distances from the other nodes (lines[4-5]). Finally,
as for the eccentricity, we calculate the index i
min
of
the minimum value in L
C
. Such index corresponds
to the center c
C
in G. Referring again to our exam-
ple, given the matrix M by the Floyd-Warshall algo-
rithm, we have the following closeness vector L
C
=
∞ ∞ ∞ 11 ∞ ∞ ∞ ∞ ∞
t
. Since the
minimum value is 11, i
min
is 4 (i.e. the center is K I).
Centroid Values. The last centrality index presented
here is used in competitive settings. Suppose each
vertex represents a customer in a graph. The service
location problem considered above assumes a single
store in a region. In reality, however, this is usually
not the case. There is often at least one competitor
offering the same products or services. Competitive
location problems deal with the planning of commer-
cial facilities which operate in such a competitive en-
vironment. For reasons of simplicity, we assume that
the competing facilities are equally attractive and that
customers prefer the facility closest to them. Con-
sider now the following situation: a salesman selects
a location for his store knowing that a competitor can
observe the selection process and decide afterwards
which location to select for her shop. Which vertex
should the salesman choose? Given a connected undi-
rected graph G of n vertices. For a pair of vertices
u and v, γ
u
(v) denotes the number of vertices which
are closer to u than to v, that is γ
u
(v) = |{w ∈ V :
d(u, w) < d(v, w)}|. If the salesman selects a vertex u
and his competitor selects a vertex v, then he will have
γ
u
(v) +
1
2
(n − γ
u
(v) − γ
v
(u)) =
1
2
n +
1
2
(γ
u
(v) − γ
v
(u))
customers. Thus, letting f (u, v) = γ
u
(v) − γ
v
(u), the
competitor will choose a vertex v which minimizes
f (u, v). The salesman knows this strategy and calcu-
lates for each vertex u the worst case, that is
c
F
(u) = min{ f (u, v) : v ∈ V − u}
c
F
(u) is called the centroid value and measures the
advantage of the location u compared to other loca-
tions, that is the minimal difference of the number of
EffectiveKeywordSearchviaRDFAnnotations
219

customers which the salesman gains or loses if he se-
lects u and a competitor chooses an appropriate ver-
tex v different from u. Based on such method, we
define a procedure to compute the center of the graph
as described in the Algorithm 3. In the algorithm, we
initialize the centroid vector min and the centroid ma-
trix C, i.e. n × n, where each value [i,j] corresponds
to f (i, j). We fill C (lines[5-15]) by using the ma-
trix M, calculated by the Floyd-Warshall algorithm.
Then for each row i of C we copy the minimum value
in min[i] (lines[16-17]). Finally we calculate the in-
dex i
max
corresponding to the maximum value in min
(line[18]). The center c
F
correspond to the node in V
with index i
max
. Referring again to our example, we
have the following matrix
C =
0 0 0 −7 0 −4 −4 0 0
0 0 0 −7 0 −4 −4 0 0
0 0 0 −7 0 −4 −4 0 0
7 7 7 0 7 0 3 7 7
0 0 0 −7 0 −4 −4 0 0
4 4 4 0 4 0 2 4 4
4 4 4 −3 4 −2 0 4 4
0 0 0 −7 0 −4 −4 0 0
0 0 0 −7 0 −4 −4 0 0
from C we compute the following vector min =
−7 −7 −7 0 −7 0 −3 −7 −7
t
.
In this case the minimum value is 0, corresponding to
two indexes: 4 and 6. This means that we have two
centroids, i.e. K
I and K E I.
3.2 Effective Navigation of Web Pages
The methods discussed above compute the center of a
graph with respect to the topology and “spatial” in-
formation on the nodes. Referring to the example
in Figure 2, in any method we have the center K I
(the centroid method reports K E I also). In this case
such center allows to reach all nodes of the graph, but
the navigation starting from such center is not effec-
tive: K I corresponds to the Web page with all Ken-
neth Iverson. The best starting point would be K E I
that is the Kenneth Iverson directly linked to the APL
programming language page. Therefore beyond the
center based on the spatial information of the graph,
we need a “center of interest”, i.e. some vertex that
is more closed to the significant pages than others.
In other words we need the node that is close to the
nodes having high scores. Therefore, we compute the
center of interest as described in the Algorithm 4.
In the algorithm, we calculate the closeness of
each node, that is the sum of distances from the oth-
ers but we normalize it with respect to the score of
the node (lines[5-13]): the center of interest will have
the minimum closeness with the highest score. If
the node with index i we are considering has score
Algorithm 3: Center computation by centroid
values.
Input : The graph G
Output: The center c
F
1 n ← V.length;
2 C ← InitializeMatrix(n,n);
3 min ← InitializeArray(n);
4 M ← FloydWarshall(G);
5 for i ← 0 to n do
6 for j ← 0 to n do
7 if i == j then
8 C[i][ j] ← ∞;
9 else
10 for h ← 0 to n do
11 if h 6= i ∧ h 6= j then
12 if M[i][h] ¡ M[j][h] then
13 C[i][j] ¡ ← C[i][j] +1;
14 else if M[i][h] ¿ M[j][h]
then
15 C[i][j] ¡ ← C[i][j] -1;
16 for i ← 0 to n do
17 min[i] ← Min(C[i]);
18 i
max
← MaxIndex(min);
19 c
F
← V [i
max
];
20 return c
F
;
Algorithm 4: Center of interest.
Input : The graph G.
Output: The center of interest c.
1 n ← V.length;
2 D ← InitializeArray(n);
3 M ← FloydWarshall(G);
4 min ← 0;
5 for i ← 0 to n do
6 D[i] ← 0;
7 if ω(V [i]) > 0 then
8 for j ← 0 to n do
9 if ω(V [ j]) > 0 then
10 D[i] ← D[i] + M[i][ j];
11 D[i] ←
D[i]
ω(V [i])
;
12 else
13 D[i] ← ∞;
14 i
min
← MinIndex(D);
15 c ← V [i
min
];
16 return c;
DATA2012-InternationalConferenceonDataTechnologiesandApplications
220

!"
#!"
$!"
%!"
&!"
'!!"
'#!"
'$!"
'%!"
'&!"
'!"
(!"
'!!"
'(!"
#!!"
)*+,)-+",+./01.+"23+"43.5"
6"107+."
+88+19,:8:9;"
8<0.+1+.."
8+19,0:7"
:19+,+.9"
Figure 3: Performance of the approach.
0 then the closeness is ∞. We store all values into the
vector D, initialized by InitializeArray(line[2]).
Finally we calculate the index i
min
corresponding to
the minimum value in D and the center of interest
c will be the node in V with index i
min
. Referring
again to our example we have the following vector
D =
∞ ∞ ∞
8
2
12
1
6
2
9
1
10
1
9
1
t
. Since
the minimum value is 3 (i.e.
6
2
) the center of interest
has index 6, that is the node K E I. The joint use of
the center calculated by spatial methods (i.e. eccen-
tricity, closeness and centroid values) and the center
of interest allows an effective navigation of the result.
4 EXPERIMENTAL RESULTS
We implemented our framework in a Java tool
1
. The
tool is according to a client-server architecture. At
client-side, we have a Web interface based on GWT
that provides (i) support for submitting a query, (ii)
support for retrieving the result and (iii) a graphical
view to navigate the Web pages via the resulting anno-
tation. At server-side, we have the core of our query
engine. We used YAANII (De Virgilio et al., 2009),
a system for keyword search over RDF graphs. We
have executed several experiments to test the perfor-
mance of our tool. Our benchmarking system is a
dual core 2.66GHz Intel with 2 GB of main mem-
ory running on Linux. We have used Wikipedia3, a
conversion of the English Wikipedia into RDF. This
is a monthly updated data set containing around 47
million triples. The user can submit a keyword search
query Q to YAANII that returns the top-10 solutions.
Each solution is a connected subgraph of Wikipedia3
matching Q. In Figure 3 we show the performance of
our system to compute the centrality indices. In par-
ticular we measured the average response time (ms) of
ten runs to calculate the center in any method. Then,
publishing the system on the Web, we asked to several
and different users (i.e. about 100) to test the tool by
providing a set of ten keyword search queries and to
1
A video tutorial is available at
http://www.youtube.com/watch?v=CpJhVhx3r80
Figure 4: Effectiveness of the approach.
indicate if the centers are really effective. In this way
we calculates the interpolation between precision and
recall as shown in Figure 4. All these results validates
the feasibility and effectiveness of our approach.
5 CONCLUSIONS AND FUTURE
WORK
In this paper we discussed and implemented an ap-
proach for an effective navigation of Web pages by
using semantic annotations. The approach is based on
defining and implementing centrality indices, allow-
ing the user to automatically select the starting point
from which to reach the Web pages of interest. Ex-
perimental results demonstrate how it is significant
the use of semantic annotations for surfing the Web
effectively. In particular, an effective visualization of
the annotation matching the user request improves the
quality of the navigation. For future work, we are
investigating new methods to individuate the starting
point in distributed architectures.
REFERENCES
Bavelas, A. (1950). Communication patterns in task ori-
ented groups. Journal of the Acoustical Society of
America, 22:271–282.
Beauchamp, M. A. (1965). An improved index of centrality.
Behavioral Science, 10:161–163.
Cappellari, P., De Virgilio, R., Maccioni, A., and Roantree,
M. (2011). A path-oriented rdf index for keyword
search query processing. In DEXA, pages 366–380.
De Virgilio, R., Cappellari, P., and Miscione, M.
(2009). Cluster-based exploration for effective key-
word search over semantic datasets. In ER, pages 205–
218.
De Virgilio, R., Giunchiglia, F., and Tanca, L., editors
(2010). Semantic Web Information Management - A
Model-Based Perspective. Springer.
Domschke, W. and Drexl, A. (1985). Location and Layout
Planning: An International Bibliography. Springer-
Verlag, Berlin.
Harary, F. and Hage, P. (1995). Eccentricity and centrality
in networks. Social Networks, 17:57–63.
EffectiveKeywordSearchviaRDFAnnotations
221

Herlihy, M. (1964). Optimum location of switching cen-
ters and the absolute centers and medians of a graph.
Operations Research, 12:450–459.
Li, W.-S., Candan, K. S., Vu, Q., and Agrawal, D. (2001).
Retrieving and organizing web pages by “information
unit”. In International World Wide Web Conferences
(WWW), pages 230–244.
Moxley, R. L. and Moxley, N. F. (1974). Determining point-
centrality in uncontrived social networks. Sociometry,
37:122–130.
Rosen, K. H. (2003). Discrete Mathematics and Its Appli-
cations. Addison Wesley.
Sabidussi, G. (1966). The centrality index of a graph. Psy-
chometrika, 31:581–603.
Smart, C. and Slater, P. J. (1999). Center, median and cen-
troid subgraphs. Networks, 34:303–311.
Valente, T. W. and Foreman, R. K. (1998). Integration and
radiality. Social Networks, 1:89–105.
DATA2012-InternationalConferenceonDataTechnologiesandApplications
222
