
Robot Phase Entrainment on Quadruped CPG Controller
Vítor Matos and Cristina P. Santos
Industrial Electronics Department, School of Engineering, University of Minho, Guimarães, Portugal
Keywords:
Central Pattern Generator, Quadruped locomotion, Locomotion Entrainment.
Abstract:
Central Pattern Generators are used in several kinds of robot locomotion, from swimming and flying, to bipeds,
quadrupeds and hexapods. It is thought that this approach can yield better results in dynamical and natural
environments. In this work we expand a previous quadruped locomotion controller and propose a method
to couple the step cycle phase onto the locomotor CPG of a quadruped robot, creating a feedback pathway
to coordinate the phases of each leg to the phase of the step cycle. This approach is tested in a simulated
quadruped robot and the performed locomotion is evaluated. Results demonstrate that the proposed phase
coupling synchronizes the swing step phase of ipsilateral legs to the respective step phase of the cycle and
show an improvement in stability of the performed walk gait.
1 INTRODUCTION
Motor control is a complex problem in robotics,
highly relevant in tasks such as manipulation and
grasping, environment exploration and navigation,
human-robot interaction and locomotion, all in de-
manding dynamical environments. Several processes
must be addressed to achieve an acceptable level of
performance and autonomy in motor control, as per-
ception, planning, execution, feedback and mechan-
ics.
We endeavor to achieve general and autonomous
quadruped locomotion on natural environments. In
this work we explore further contributions in the
feedback process, ubiquitous for short and long-term
adaptation of any kind of legged locomotion.
Legged locomotion can be achieved using typi-
cal model based planning algorithms (Buchli et al.,
2009), or limit-cycle based control, such as Central
Pattern Generators (CPGs) (Fukuoka et al., 2003).
CPG controllers are well suited for locomotion be-
cause: 1) produce stable rhythmic patterns, provid-
ing robustness against transient perturbations; 2) en-
able the design of distributed implementations; 3) are
generally easier to modulate through control param-
eters that may be used as higher level command sig-
nals; and 4) due to its stability, CPGs are appropri-
ate for the integration of sensory feedback signals
and to achieve entrainment with the mechanical body
(Ijspeert, 2008).
CPG systems can be designed starting from dif-
ferent conceptual approaches. They can be designed
firstly from the CPG model as a feedforward gen-
erator, and only then the effect of feedback signals
is included and the loop is closed; endorsing what
kind of information should be considered and how
will affect the final behaviour (Righetti and Ijspeert,
2008; Fukuoka et al., 2003). Or can be designed
from the beginning with the closed-loop goal in mind,
using feedback signals to tightly generate trajecto-
ries (Maufroy et al., 2010; Buchli and Ijspeert, 2008).
Systems of coupled oscillators are widely used
for modeling CPGs, and while there exists exten-
sive work and methods for analyzing these dynamical
systems, less work has been carried out on methods
and frameworks for synthesizing oscillators that have
to exhibit a specific desired behavior. For instance,
in (Buchli et al., 2006) it is presented a framework
for characterizing and designing oscillators, as well
as defining desired perturbations in order to achieve
frequency-locking, phase-locking or any specific out-
put signal shape.
Step phase feedback plays an important role in lo-
comotion, allowing the adaptation of the onset of the
swing and stance phases (Pearson, 2008). These were
explored in legged robots, whether through phase re-
setting (Aoi and Tsuchiya, 2006) or phase transitions
depending on load/unloading of the legs (Righetti and
Ijspeert, 2008; Maufroy et al., 2010)
In this paper, we explore a different approach for
phase feedback. We devise a phase feedback inspired
in (Fukuoka et al., 2003) and try to entrain the CPG
260
Matos V. and P. Santos C..
Robot Phase Entrainment on Quadruped CPG Controller.
DOI: 10.5220/0004037802600265
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 260-265
ISBN: 978-989-8565-22-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

oscillators with the phase of the robot’s periodic dy-
namics, coordinating the phase of the step cycle of
each leg with the sensed body motion.
The goal of this contribution is to include step
phase feedback onto a previous developed locomotor
system and study its influence on locomotion’s per-
formance. It is based on past work for modeling a
limb-CPG (Matos and Santos, 2010). This previous
work only considered the CPG network as a rhythmic
open-loop controller. In this paper, we discuss the ef-
fects of the addition of feedback on the rhythmogenic
ability of the CPGs, and propose a methodology to
explore the possibilities of physical entrainment with
the system.
The proposed feedback couples the CPG system
to the pendulum rolling motion of the projected Cen-
ter of Gravity (pCOG). Robot’s sensory information
regarding body angle, joint position and foot touch
sensors are used to calculate pCOG, which modu-
lates the frequency of the leg oscillator through the
feedback mechanism. The goal of this feedback is to
avoid the swinging of a leg before the robot pCOG is
transferred to the opposite supportpolygon, and this is
achieved by synchronizing the oscillator’s phase with
the performed step phase.
The inclusion of feedback is expected to improve
robot performance, herein measured by the Support
Stability Margin (SSM), an adequate measure for a
static stable. Besides, the proposed feedback should
not affect the required duty factor and phase relation-
ships of a crawl gait.
Simulations are conducted on a simulated en-
vironment with the model of an AIBO quadruped
robot. We study the robot’s performance regarding
velocity, SSM and the correct execution of the step
phases. We also explore the influence of integrat-
ing this phase feedback along with the coupling net-
work of CPGs (Matos and Santos, 2010). Simulation
results show an improvement on robot performance
regarding SSM, maintaining the desired general fea-
tures of the crawl gait such as duty factor and inter-
limb phase relationships.
2 LOCOMOTOR SYSTEM
The locomotor system generates the trajectories for
the leg joints, producing the locomotor motions of the
robot. Similarly to previous work, the locomotor sys-
tem is composed by a network of four Central Pat-
tern Generators (CPGs) modeled as nonlinear oscil-
lators (Matos and Santos, 2010). Each CPG is able
to endogenously output the rhythmic signals that will
control each joint on a single leg.
2.1 Central Pattern Generator
The concept of biological locomotor CPG includes
the idea of hierarchical organized unitary oscillators,
the unit-CPG. A single unit-CPG controls and acti-
vates the antagonistic muscle pairs, controlling the
movements of a single joint.
The hip unit-CPG is modeled using a nonlinear
oscillator:
˙x
i
= α
µ−r
2
i
(x
i
−O
i
) −ω
i
z
i
(1)
˙z
i
= α
µ−r
2
i
z
i
+ ω
i
(x
i
−O
i
) (2)
ω
i
=
1−β
β
ω
sw
e
−az
i
+ 1
+
ω
sw
e
az
i
+ 1
, (3)
with r
i
=
q
(x
i
−O
i
)
2
+ z
2
i
.
x(t)
i
solution is the angle of the hip joint of leg
i at instant t. This rhythmic solution has an ampli-
tude of
√
µ, an offset O
i
and an angular frequency
ω. Frequency is modulated according to the current
phase of the oscillator, enabling the generation of a
trajectory with stance and swing phase of different
durations (Righetti and Ijspeert, 2008). We want to
achieve a 0.75 duty factor for the walk gait, setting
β = 0.75. Parameter α controls the relaxation of the
solution to the stable orbit and a the toggling speed of
ω.
The modulation of the generated trajectories with
respect to their amplitude, frequency and offset, is
carried out explicitly and smoothly through the speci-
fication of a set of parameters, and allows for a dis-
tributed organization due to its entrainment proper-
ties.
Knee joints are controlled according to the corre-
sponding hip swing joint in a simple fashion. When
the leg performs the swing phase, the knee flexes to
a fixed angle θ
sw
. During the stance phase, the knee
extends to θ
st
.
This motion is generated by applying the follow-
ing second order system:
˙y
i
= v
i
, ˙v
i
= −
b
2
4
(y
i
−g
i
) −bv
i
(4)
g
i
=
θ
st
e
−az
i
+1
+
θ
sw
e
az
i
+1
(5)
whose stable solution y converges to a goal fixed
point g, changing between θ
sw
and θ
st
depending on
the step phase. Relaxation is controlled by parameter
b.
2.2 Interlimb Coordination
In order to generate the desired quadruped gait, we
couple the four CPGs in a network with variable phase
RobotPhaseEntrainmentonQuadrupedCPGController
261

Table 1: Phase relationships for walking gait.
i LF LF LF RF RF LH
j RF LH RH LH RH RH
φ
j
i
−π −
3π
2
−
π
2
−
π
2
π
2
π
relationships. Coupling between two oscillators is
achieved by applying a rotation matrix R
φ
j
i
, where
φ
j
i
is the desired relative phase between oscillator i
and j. Eqs (1,2) are extended with the rotation matrix
members:
˙x
i
= . . . + k
osc
∑
j6=i
x
j
cosφ
j
i
−z
j
sinφ
j
i
, (6)
˙z
i
= . . . + k
osc
∑
j6=i
x
j
sinφ
j
i
+ z
j
cosφ
j
i
, (7)
where i and j specifies the CPG of leg ∈
{LF, RF, LH, RH}. Parameter k
osc
determines the
strength of the interlimb coupling in the network,
where every connection has equal weight. Phase re-
lationships for the walk gait are presented in table 1,
note that φ
j
i
= −φ
i
j
.
The achievedcoordination among the CPGs is sta-
ble and flexible through the modulation of the desired
phase relationships. It is also stable and robust to
perturbations of phase, making the system return to
the desired phase relationships, dependingon the cou-
pling strength k
osc
and assuming a limited range in the
perturbation magnitude.
2.3 Robot Phase Coupling
The goal of using phase coupling in our CPG ap-
proach is to synchronize the phases of the CPG net-
work to the dynamics’ phase of the robot. The act
of walking exhibits periodic motions, from which we
extract the phase of the robot’s locomotion or robot
phase. We use the periodic motion of the projected
Center of Gravity to calculate the robot’s phase, con-
sidering the body angle, joint positions and touch sen-
sors. The proposed coupling tries to synchronize the
generated swing phase of the CPGs with the measured
point in the step cycle in which the robot has its pro-
jected Center of Gravity (pCOG) over the contralat-
eral support polygon during the walk gait (fig. 1).
If this phase coupling is achieved correctly, the
swing phase of each leg will happen when the pCOG
is over the contralateral support side, ensuring that the
weight is not over the swinging leg, and thus the robot
does not fall over it. This feedback mechanism by co-
ordinating the swing phases with the correct support
polygon presents the potential of improving the walk,
by increasing the stability, forcing the pCOG to be
over the side with most legs supporting the body. This
x
y
A B C D E
Figure 1: Oscillatory movement exhibited by the pro-
jected Center of Gravity during the walk gait. The pCOG
moves between the contralateral triangular support poly-
gons. Open circles denote feet ground contact.
improvement on stability is specially desired when
the body weight goes from one side to the other (A
to B in fig. 1). The normal tendency is to fall over
the swing leg. The proposed feedback is expected to
improve this.
To achieve this kind of entrainment between our
oscillators and the robot dynamics we follow the gen-
eral guidelines from (Buchli et al., 2006). We spec-
ify the desired perturbation effect on the oscillator’s
phase using its polar representation and transform it
back to its cartesian representation.
Consider the oscillator from eq.(1,2) in polar co-
ordinates and consider the movement of pCOG in the
frontal plane due to the robot’s rolling motion as a
simple oscillatory motion with its phase described by
φ
r
= arctan2
˙
pCOG
y
pCOG
y
. We couple the robot’s phase
(φ
r
) with the oscillator’s phase (φ
i
) with a desired
phase difference of φ
i
r
and coupling constant k
r
, as fol-
lows:
˙
φ
i
= ω
i
+ k
r
sin
φ
r
−φ
i
−φ
i
r
, (8)
˙r
i
= α
µ−r
2
i
r
i
. (9)
In cartesian coordinates this phase coupling be-
comes
˙x
i
= α
µ−r
2
i
(x
i
−O
i
) −z
i
ω
i
, (10)
˙z
i
= α
µ−r
2
i
z
i
−(x
i
−O
i
)ω
i
, (11)
ω
i
= ω
i
−
k
r
r
i
h
z
i
cos
φ
r
+ φ
i
r
−x
i
sin
φ
r
+ φ
i
r
i
. (12)
We choose the desired phase differences to respect
the followingrules (fig. 2): i) when the robot leans left
with its pCOG over the left support polygons, φ
r
= 0,
the right legs should perform the swing phase, −π <
φ
i
< 0; ii) when the robot leans right and the pCOG
is to the right side, φ
r
= π, the left legs should swing
while the right legs perform the stance phase, −π <
φ
i
< 0; and iii) the oscillators should reflect the phase
relationship and sequence of the walk gait and exhibit
a relative phase difference of
π
2
among themselves.
Phase relationships are: φ
LF
r
=
π
4
, φ
RF
r
=
−3π
4
, φ
LH
r
=
3π
4
, φ
RH
r
=
−π
4
.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
262

Swing Stance
Á
r
=0 Á
r
=¼
pCOGy
pCOGy
.
pCOGy
pCOGy
.
pCOG over left pCOG over right
LH LF
RF RH
RH RF
LF LH
Figure 2: Limit cycle of the pCOG oscillation on the
frontal plane (pCOG
y
). When the pCOG is on the left side
(pCOG
y
> 0) the robot’s phase is φ
r
= 0 , and φ
r
= π when
is on the right side pCOG
y
< 0. Each CPG performs the
swing phase when −π < φ
i
< 0.
3 SIMULATIONS
A series of simulations were performed in a sim-
ulated environment with the model of Sony AIBO
quadruped robot in Webots
1
.
First we study the coupling of interlimb coordi-
nation and robot phase by changing the values of the
coupling weights k
osc
, k
r
. We make a systematic pa-
rameter exploration on the parameter tuple hk
osc
, k
r
iin
the range [0, 9.5], in steps of 0.5. In each run the robot
locomotes with a desired nominal gait, a statically sta-
ble walk gait (β = 0.75) for 10 s and the required in-
formation is recorded. We then compare and discuss
the obtained average Support Stability Margin (SSM)
and the achieved velocities. SSM is the smallest dis-
tance of the pCOG to the edge of the polygon defined
by the supporting feet projection onto the plane with
the gravitational acceleration as its normal. SSM is
an indicator that tells if the pCOG is inside the sup-
port polygon at all times, when considering statically
stable gaits as the walking gait.
We then choose and use the hk
osc
, k
r
i values that
result in the best walk in terms of trade-off between
the average SSM and the achieved velocity, to com-
pare and quantify the improvement of the walk with-
out and with robot phase coupling. We analyze the
robot’s performance regarding velocity, SSM and dis-
cuss improvements over the execution of the step
phases.
Parameter Exploration. Interlimb coupling, k
osc
,
and robot phase coupling, k
r
influence the walk in
different ways. While interlimb coupling simply co-
ordinates the phase relationships between the CPGs,
robot phase coupling tries to coordinate the phase of
each CPG to the phase of the robot.
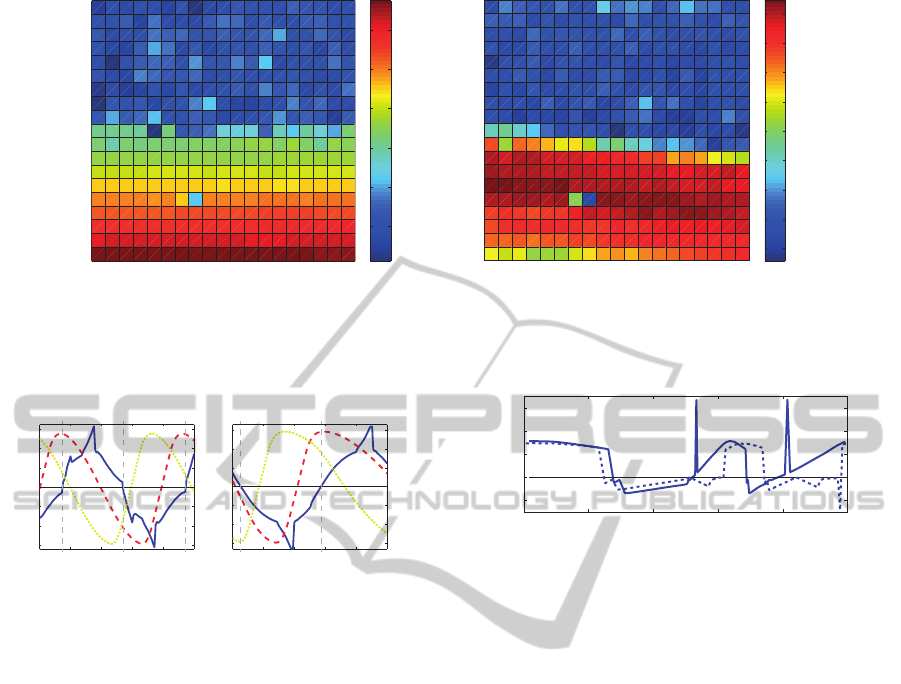
From fig. 3(a) we can see that velocity does not
1
Webots mobile robot simulator: http://
www.cyberbotics.com/
change when we increase or decrease the strength of
interlimb coupling, k
osc
. However, when changing
the strength of phase coupling, k
r
, the achieved ve-
locity is influenced, decreasing when the coupling in-
creases. This is a possible indicator that the oscillators
are being adapted to respect the current step phase of
the walk, being slowed down to match the robot dy-
namics. For k
r
> 4.5 the velocity decreases greatly,
suggesting that beyond this point the influence and
strength of this phase coupling is no longer adequate
and tries to stop the robot.
Similarly, SSM shows no major variation for a
changing interlimb coupling strength, k
osc
(fig. 3(b)).
The major determinant of the achieved SSM is the
phase coupling strength, k
r
. There is a range of k
r
where the SSM shows higher values, [1;3.5]. It sug-
gests that the CPGs are being coordinated according
to the robot dynamics, correcting the execution of the
step phases. However, above 3.5 the SSM decreases
to low values, similarly to the velocity.
The velocity achieved without phase coupling was
0.134 m.s
−1
(k
osc
= 1, k
r
= 0) and the obtained SSM
was 6.14 mm. The highest obtained SSM was
12.97 mm, when using k
osc
= 2.5, k
r
= 2.5, with
achieved velocity 0.098 m.s
−1
. We consider this re-
sult to be a fair trade-off between the achieved SSM
and velocity for a walk gait.
Locomotion Comparison. With phase coupling
(k
osc
= 2.5, k
r
= 2.5) it is expected that the left legs’
swing phases are performed when the pCOG is over
to the right side of the support polygon. We can ver-
ify this is true in fig. 4 (right) since the swing phase of
both left legs (ascending trajectories) are performed
when pCOG
y
< 0. These results show that the pro-
posed phase coupling synchronizes the swing step
phase of ipsilateral legs to the respective step phase
of the cycle. The nominal step period is 0.8 s, from a
swing period of 0.2 s and a duty factor of 0.75. When
we employphase coupling the interaction of the CPGs
with the robot’s phase changes slightly the achieved
average step period, from 0.8 s to 1.2 s, while main-
taining the chosen duty factor, adapting the swing pe-
riod to 0.3 s. This adaptation did not change the rela-
tive phases among the CPGs, maintaining the desired
interlimb coordination of the nominal walk gait.
Let us verify the overall effect on the achieved
step cycle duration and compare the achieved SSM.
Fig. 5 showsthe achievedSSM overthe two runs. The
dotted (solid) lines show the achieved SSM without
(with) phase coupling. Positive values denote that the
pCOG lies inside the support polygon, while negative
values denote a position outside the support polygon,
with a distance to the nearest edge correspondent to
RobotPhaseEntrainmentonQuadrupedCPGController
263
0 2 4 6 8
0
1
2
3
4
5
6
7
8
9
k
osc
k
r
0.02
0.04
0.06
0.08
0.1
0.12
(a) Velocity achieved on each run.
0 2 4 6 8
0
1
2
3
4
5
6
7
8
9
k
osc
k
r
−4
−2
0
2
4
6
8
10
12
(b) Mean Support Stability Margin (SSM) on each run.
Figure 3: k
osc
, k
r
parameter exploration, and its effects on velocity (m.s
−1
) and phase coupling. Velocity and SSM are mostly
influenced by the value of k
r
.
8 8.2 8.4 8.6 8.8 9
−15
−10
−5
0
5
10
15
8 8.2 8.4 8.6 8.8 9
−15
−10
−5
0
5
10
15
pCOG
y
, Left joints
Time (s)
left rightright leftright
Without feedback With feedback
Figure 4: pCOG position in the frontal plane (solid blue)
and left hip joints’ trajectories (dashed red:fore and dotted
yellow:hind). Swing phases correspond to the ascending
parts of the trajectories. Without phase coupling the hind
leg (dotted yellow) swing onset happens while the pCOG
is in the ipsilateral side (left panel), meaning pCOG
y
> 0.
With phase coupling (right panel) the swing phases on both
left legs happen when the pCOG is in the contralateral side,
pCOG
y
< 0.
the absolute value.
We can verify in fig. 5 that the performed SSM in-
creases when phase coupling is employed. Negative
values of SSM indicate the robot may fall over the
swinging leg. The moments of the step where pCOG
falls outside the support polygon (negativevalues) are
reduced from 66% of the step phase without feedback
(dotted), to 29% of step phase when feedback is em-
ployed (solid). The average value of SSM also in-
creases due to the maintenance of the pCOG inside
the support polygon.
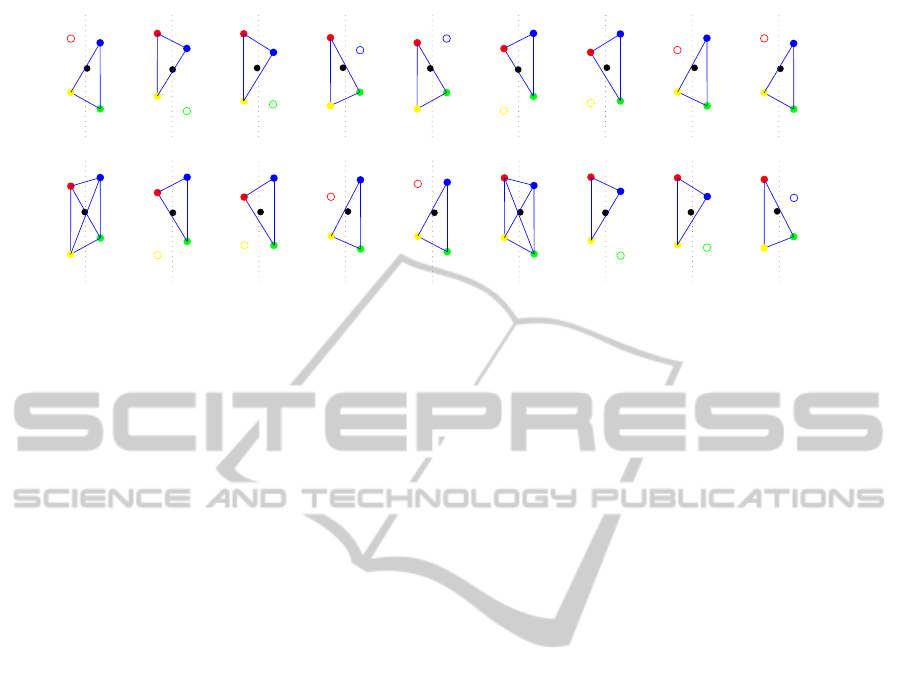
The walk gait sequences from the two simulations
are shown in fig. 6. We can see that without phase
coupling (top) the pCOG is generally closer to the
edge of the support polygon than with phase coupling
(bottom). pCOG also is in the same side in the onset
of some swing phases when phase coupling is not em-
ployed, at 9.10 s and 9.50 s, which was solved when
phase coupling is employed (bottom, at 9.10 s and
9.60 s). The concerning point of contralateral swing
0 0.2 0.4 0.6 0.8 1
−20
0
20
40
60
Step cycle
SSM (mm)
Figure 5: SMM without (dotted) and with (solid) robot
phase coupling. The average SSM is 6.14 mm without
phase coupling and 12.97 mm with phase coupling. Us-
ing phase coupling, increases the chance of brief four feet
support (solid).
onset was dealt with by the proposed feedback mech-
anism and the result was to achieve brief four feet
support between these contralateral phases (bottom,
at 9.00 s and 9.50 s).
Results also show that front feet touching the
ground incorrectly during the swing phase decreased
from 12.60% to 11.90% of the swing phase period,
and hind feet from 1.30% to 0.07%. The unwanted
lifting of the feet occurring during stance phase de-
creased in the fore legs from 23.40% to 5.09% of the
stance period.
4 CONCLUSIONS
In this contribution we try to take advantage of the
properties of oscillators, typically used to model
CPGs on legged robots. We investigate and propose
a method to couple the CPG rhythmic activity to the
step phase of a quadruped robot, trying to create a link
between the robot dynamics and the walking motion
of the locomotor controller.The goal of the proposed
feedback is to maintain the pCOG over the contralat-
eral side of the current swinging leg, in order to im-
prove stability and avoid the swinging of a leg which
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
264
9.00 s
9.10 s
9.20 s
9.30 s 9.40 s
9.50 s
9.60 s
9.70 s
9.80 s
9.00 s 9.10 s 9.20 s 9.30 s 9.40 s 9.50 s 9.60 s 9.70 s 9.80 s
Figure 6: Performed gait sequence of the walk gait without (top) and with (bottom) phase coupling. Black dot is the position
of the projected Center of Mass. Colored filled dots represent stance trajectories and empty dots swing trajectories. (red:left
fore, blue: right fore, yellow:left hind, green: right hind) In this figure, the reference frame is centered on the robot.
is supporting the body weight.
Results show that the phase coupling adapts the
generated trajectories and performs what is proposed.
A systematic exploration of coupling parameters was
conducted to study the influence of interlimb coupling
and the proposed phase coupling onto the CPG and
final walk gait, and the best parameters were used to
conduct further comparisons. The obtained measure-
ments indicate an improvement of the walk gait, dou-
bling the SSM.
However,further work should be performed in
evaluating its effect on different walking conditions,
such as in inclined planes, irregular terrains and small
perturbations. We will also study the integration with
other kinds of feedback within the same framework,
such as phase transition (Righetti and Ijspeert, 2008)
and postural control (Sousa et al., 2010), as well as on
other legged robots, including robots with compliant
actuators.
ACKNOWLEDGEMENTS
This work is funded by FEDER Funding supported
by the Operational Program Competitive Factors -
COMPETE and National Funding supported by the
FCT - Portuguese Science Foundation throughproject
PTDC/EEACRO/100655/2008. Vítor Matos is sup-
ported by PhD Grant SFRH/BD/62047/2009, granted
by the Portuguese Science Foundation.
REFERENCES
Aoi, S. and Tsuchiya, K. (2006). Stability analysis of a sim-
ple walking model driven by an oscillator with a phase
reset using sensory feedback. IEEE Transactions on
Robotics, 22(2):391 – 397.
Buchli, J. and Ijspeert, A. J. (2008). Self-organized adaptive
legged locomotion in a compliant quadruped robot.
Auton. Robots, 25:331–347.
Buchli, J., Kalakrishnan, M., Mistry, M., Pastor, P., and
Schaal, S. (2009). Compliant quadruped locomotion
over rough terrain. In 2009 IEEE/RSJ international
conference on Intelligent robots and systems, pages
814–820.
Buchli, J., Righetti, L., and Ijspeert, A. J. (2006). Engineer-
ing entrainment and adaptation in limit cycle systems:
From biological inspiration to applications in robotics.
Biol. Cybern., 95:645–664.
Fukuoka, Y., Kimura, H., and Cohen, A. H. (2003). Adap-
tive dynamic walking of a quadruped robot on irregu-
lar terrain based on biological concepts. I. J. Robotic
Res., 22(3-4):187–202.
Ijspeert, A. J. (2008). Central pattern generators for loco-
motion control in animals and robots: a review. Neu-
ral Networks, 21(4):642–653.
Matos, V. and Santos, C. (2010). Omnidirectional locomo-
tion in a quadruped robot: A cpg-based approach. In
2010 IEEE/RSJ International Conference on Intelli-
gent Robots and Systems, pages 3392 –3397.
Maufroy, C., Kimura, H., and Takase, K. (2010). Inte-
gration of posture and rhythmic motion controls in
quadrupedal dynamic walking using phase modula-
tions based on leg loading/unloading. Auton. Robots,
28:331–353.
Pearson, K. (2008). Role of sensory feedback in the control
of stance duration in walking cats. Brain Research
Reviews, 57(1):222 – 227.
Righetti, L. and Ijspeert, A. J. (2008). Pattern generators
with sensory feedback for the control of quadruped
locomotion. In 2008 IEEE International Conference
on Robotics and Automation, pages 819–824.
Sousa, J., Matos, V., and Peixoto dos Santos, C. (2010).
A bio-inspired postural control for a quadruped robot:
An attractor-based dynamics. In 2010 IEEE/RSJ In-
ternational Conference on Intelligent Robots and Sys-
tems, pages 5329 –5334.
RobotPhaseEntrainmentonQuadrupedCPGController
265
