
Performance Evaluation of Discrete Event Systems Thanks to New
Representations for (max,+) Automata
Rabah Boukra, S´ebastien Lahaye and Jean-Louis Boimond
LISA, Universit´e d’Angers, 62 Avenue Notre Dame du Lac, Angers, France
Keywords:
Discrete Event System, Performance Evaluation, (max,+) automaton.
Abstract:
In this contribution, we study the performances of discrete event systems modeled by (max,+) automata.
More precisely, new representations for (max,+) automata are first proposed. From these, several performance
indicators can be derived, in particular the maximum time execution and a minorant of the minimum execution
time for a sequence of length n. Finally these results are discussed in comparison with several studies of the
literature also dealing with performance evaluation of (max,+) automata.
1 INTRODUCTION
At a certain abstraction level, the dynamics of many
systems is driven by decisions in reaction to events
occurrences. We speak of Discrete Event Systems
(DES), and typical examples are manufacturing sys-
tems, transportation networks, computer networks
(Cassandras and Lafortune, 2008). The motivations
can be to identify properties, to analyze and/or to con-
trol DES. Different modeling formalisms are used in
the literature. In particular, models using (max,+) al-
gebra have been successfully applied to the perfor-
mance evaluation of DES. Let us mention among oth-
ers:
• the monograph (Baccelli et al., 1992) for DES
which can be modeled by timed event graphs;
• the articles (Gaubert, 1995), (Su and Woeginger,
2011) for DES modeled by (max,+) automata.
The last two works use (max,+) automata as mod-
els in order to determine performance indicators, such
as the maximum execution time and the minimum ex-
ecution time for a sequence of n events, (resp. the
maximum and minimum makespan).
In this contribution, the framework is identical,
that is, we are interested in performance analysis
thanks to models corresponding to automata with
weights in (max,+) algebra.
More precisely, recursive equations over (max,+)
algebra are proposed to model extremal behaviors of a
(max,+) automaton. These constitute representations,
which are, to the best of our knowledge, original, and
which easily allow us to derive some performance in-
dicators, among which the maximum execution time
and a minorant for the minimum execution time.
This paper is organized as follows. In the next
section, preliminaries on dioids are recalled together
with (max,+) automata and their properties. In Sec-
tion 3, the new representations for (max,+) automata
are introduced. These naturally lead to some perfor-
mance evaluation elements described in Section 4. A
conclusion and some prospects are given in Section 5.
2 PRELIMINARIES
2.1 Dioids
Necessary algebraic concepts on dioids are briefly re-
called in this section, see the monographs (Baccelli
et al., 1992) and (Heidergott et al., 2006) for an ex-
haustive presentation.
A dioid is a semiring in which the addition ⊕ is
idempotent. The addition (resp, the multiplication ⊗)
has a unit element ε (resp, e).
Example 1. The set (R ∪ {−∞}) with the maximum
playing the role of addition and conventional addition
playing the role of multiplication is a dioid, denoted
R
max
, with e = 0 and ε = −∞.
The set of n × n matrices with coefficients in R
max
,
endowed with the matrix addition and multiplication
conventionally defined from ⊕ and ⊗, is also a dioid,
denoted R
n×n
max
. The zero element for the addition is the
matrix exclusively composed of ε (= −∞). We denote
I
n
the zero element of the multiplication, which is the
505
Boukra R., Lahaye S. and Boimond J..
Performance Evaluation of Discrete Event Systems Thanks to New Representations for (max,+) Automata.
DOI: 10.5220/0004038905050510
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 505-510
ISBN: 978-989-8565-21-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
matrix with e (= 0) on the diagonal and ε (= −∞)
elsewhere.
Example 2. The set (R ∪ {+∞}), with the minimum
playing the role of addition and the conventional ad-
dition playing the role of multiplication is a dioid, de-
noted R
min
(with e = 0 and ε = +∞), usually called
(min,+) algebra.
Example 3. Formal languages over a finite alphabet
Σ are subsets of free monoid Σ
∗
, which is composed of
finite sequences of letters (called words) from Σ. The
set of formal languages, with the union of languages
playing the role of addition and concatenation of lan-
guages playing the role of multiplication, is a dioid,
denoted (Pwr(Σ
∗
),∪,.). The zero language is 0 = {},
the unit language is denoted 1 = {ε} where ε is the
empty (zero length) string.
2.2 (Max,+) Automata
Automata with multiplicities in the R
max
semiring
are called (max,+) automata. See (Gaubert, 1995) or
(Gaubert and Mairesse, 1999) for a more complete in-
troduction.
A (max,+) automaton G is a quadruple (Q,Σ,α,µ)
where
1
• Q and Σ are finite sets of states and of events ;
• α ∈ R
1×|Q|
max
is such that α
q
6= ε if q is an initial
state ;
• µ : Σ
∗
→ R
|Q|×|Q|
max
is a morphism specified by the
matrix family µ(a) ∈ R
|Q|×|Q|
max
, a ∈ Σ, knowing
that, for a string w = a
1
... a
n
, we have
µ(w) = µ(a
1
... a
n
) = µ(a
1
)... µ(a
n
),
where the matrix multiplication involved here, is
the one of R
|Q|×|Q|
max
. A coefficient [µ(a)]
qq
′
6= ε
means that, from state q, the occurrence of event
a causes a state transition to q
′
.
A (max,+) automaton is said to be deterministic if
• it has a unique initial state, namely, there is a
unique q ∈ Q such that α
q
6= ε ;
• from each state, the occurrence of an event can
not induce the occurrence of several possible state
transitions, namely, if for all a ∈ Σ each line of
µ(a) contains at most one element not equal to ε.
1
to simplify the presentation and without loss of gener-
ality, the adopted definition omits to distinguish the marked
states.
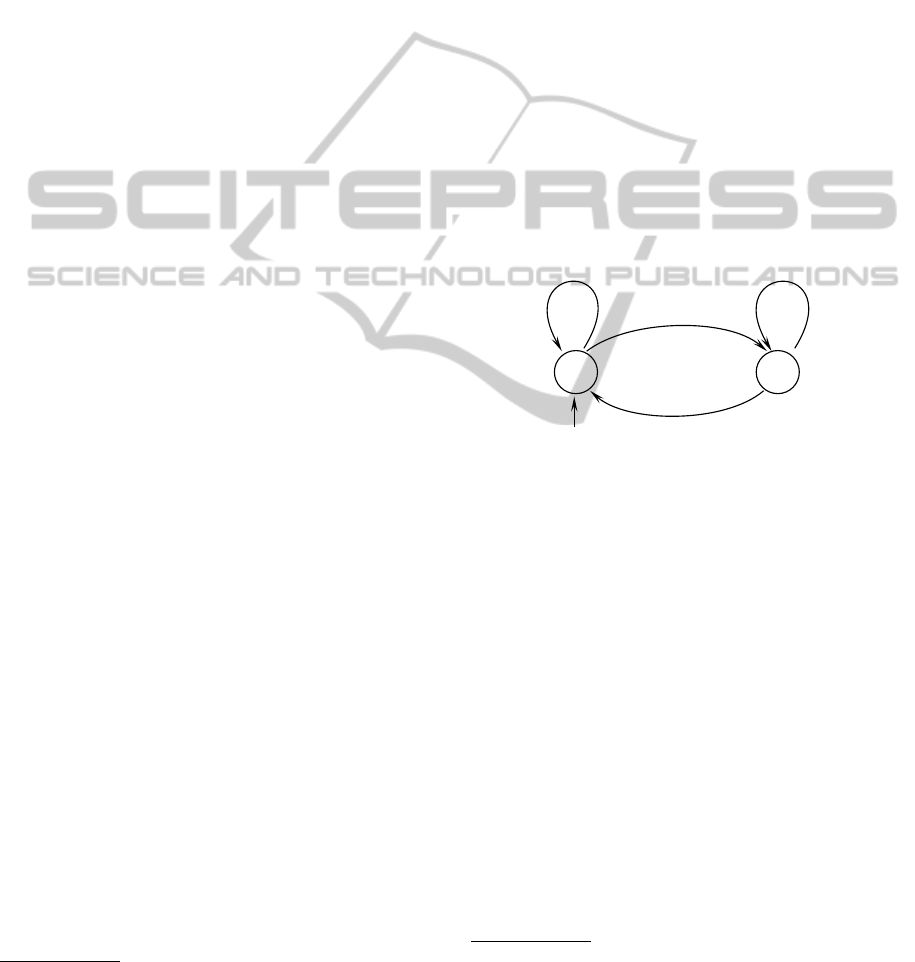
Example 4. Figure 1 is an example of graphic rep-
resentation
2
which can be associated with every
(max,+) automaton:
• the nodes correspond to states q ∈ Q ;
• an edge exists from state q ∈ Q to state q
′
if there
exists an event a ∈ Σ such that [µ(a)]
qq
′
6= ε : it
represents the state transition when event a occurs
and the value of [µ(a)]
qq
′
is interpreted as the du-
ration associated to a (namely, the time activation
of event a before it could occur) ;
• an input edge symbolizes an initial state.
For this example, we have Q = {I,II}, Σ = {a,b},
and
α =
e ε
, µ(a) =
ε 3
ε ε
,
µ(b) =
4 ε
6 2
.
The possible events sequences are the strings: b, a,
ab, ba, abb, bab, babb, abba, abab, ....
I
II
a/3
b/6
b/2b/4
Figure 1: A non deterministic (max,+) automaton.
We define x
G
(w) ∈ R
1×|Q|
max
by
x
G
(w) = αµ(w).
An element [x
G
(w)]
q
is interpreted as the date at
which the state q is reached consecutively to the
events sequence w from an initial state (with the con-
vention that [x
G
(w)]
q
= ε if the state q is not reached
consecutively to w). The elements of x
G
are general-
ized daters, and we have
x
G
(ε) = α,
x
G
(wa) = x
G
(w)µ(a).
(1)
3 NEW REPRESENTATIONS FOR
(MAX,+) AUTOMATA
Two representations which are to the best of our
knowledge original are proposed for deterministic or
2
This representation shows that (max,+) automata can
be seen as logical automata (like those considered in (Ra-
madge and Wonham, 1989)) where the time is integrated,
namely, as a class of timed automata.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
506

nondeterministic (max,+) automata. Indeed, the vari-
ables associated with (max,+) automata are different
from daters considered in (1) since they only account
for extremal behaviors.
Let us first introduce several notations. We define
the set of triples H ⊂ Q × Σ× Q as follows:
H = {(q, a,q
′
) ∈ Q× Σ × Q | [µ(a)]
qq
′
6= ε}.
A triple (q,a, q
′
) belongs to H if there exists a state
transition according to event a from state q to state q
′
.
For a given event a ∈ Σ and state q ∈ Q, we define the
set H
a,q
⊂ H by:
H
a,q
= {(r,α,s) ∈ H | α = a, s = q}.
We also define the set:
σ
n,a,q
= {[x
G
(wa)]
q
| |w| = n − 1}.
Set σ
n,a,q
contains the completion dates for sequences
of length n, starting from an initial state, ending with
event a and leading to state q, this set is a subset of
R
max
and is a chain (that is a totally ordered set).
Two representations presented below allow us to
determine in particular:
• the maximum element of this subset, that is a per-
formance indicator corresponding to the so-called
worst-case behavior for the (max,+) automaton;
• and a minorant of this subset, that is a perfor-
mance indicator related to the so-called optimal-
case behavior for the (max,+) automaton.
3.1 Representation Corresponding to
the Worst-case Behavior
We define the matrix denoted A as follows. Let A ∈
R
|H|×|H|
max
, and for j = (p,a,q) ∈ H and k = (r,a
′
,s) ∈
H
A
jk
=
(
[µ(a)]
pq
if s = p,
ε otherwise.
(2)
Example 5. The (max,+) automaton represented in
figure 1 is such that
H = {(I,b, I), (I,a, II), (II,b, II),(II,b,I)},
and
A =
4 ε ε 4
3 ε ε 3
ε 2 2 ε
ε 6 6 ε
.
For example, note that triples (II,b,I) and (I,a, II)
are listed respectively as 4th and 2nd elements in H.
Then, A
4,2
= 6 brings the information that state tran-
sition (II,b,I) can occur consecutively to the occur-
rence of state transition (I,a,II) with a duration of 6
time units.
Proposition 1. Let x(n) ∈ R
|H|×1
max
, for n ∈ N, be de-
fined iteratively by
x(1), with for j = (p,a,q),
[x(1)]
j
=
(
[µ(a)]
pq
if p is an initial state,
ε otherwise,
(3)
and
x(n) = A ⊗ x(n− 1). (4)
Then
L
j∈H
a,q
[x(n)]
j
is the maximum element of σ
n,a,q
for each a ∈ Σ and q ∈ Q.
Proof 1. We use mathematical induction to prove the
result. By construction of (3), we have
M
j∈H
a,q
[x(1)]
j
=
M
{p∈Q|p initial state}
[µ(a)]
pq
,
which corresponds to the completion date to reach the
state q upon the only occurrence of a (completion date
for the sequences of length 1, composed of a and lead-
ing to q).
Let us suppose that
L
j∈H
α,p
[x(n)]
j
is the maximum
element of σ
n,α,p
for all α ∈ Σ, p ∈ Q.
Let us show that for all a ∈ Σ, q ∈ Q,
L
j∈H
a,q
[x(n+ 1)]
j
is the maximum element of σ
n+1,a,q
.
We have:
L
j∈H
a,q
[x(n+ 1)]
j
=
L
j∈H
a,q
[A⊗ x(n)]
j
(using (4)),
=
L
j∈H
a,q
L
l∈H
[A]
jl
⊗ [x(n)]
l
,
=
L
l∈H
L
j∈H
a,q
[A]
jl
⊗ [x(n)]
l
,
=
L
p∈Q
L
α∈Σ
L
k∈H
α,p
L
j∈H
a,q
[A]
jk
⊗ [x(n)]
k
.
Notice that, by definition of (2), we have, for all
k ∈ H
α,p
,
M
j∈H
a,q
[A]
jk
=
L
p
′
∈Q
[µ(a)]
p
′
q
if p = p
′
,
ε otherwise.
Then, we deduce that
L
j∈H
a,q
[x(n+ 1)]
j
,
=
L
p∈Q
L
α∈Σ
L
k∈H
α,p
[µ(a)]
pq
⊗ [x(n)]
k
,
=
L
p∈Q
[µ(a)]
pq
⊗
L
α∈Σ
L
k∈H
α,p
[x(n)]
k
.
We know that
L
α∈Σ
L
k∈H
α,p
[x(n)]
k
represents the max-
imum completion date for sequences of length n lead-
ing to state p, so
L
j∈H
a,q
[x(n + 1)]
j
is the maximum
PerformanceEvaluationofDiscreteEventSystemsThankstoNewRepresentationsfor(max,+)Automata
507

completion date for sequences of length n + 1, end-
ing with event a and leading too state q.
Example 6. Let us consider the non determin-
istic (max,+) automaton represented in figure 1.
We have Q = {I, II}, Σ = {a,b}, and H =
{(I,b,I),(I,a,II),(II, b,II),(II, b,I)}.
Vector x(n) is written as follows:
x(n) =
x
I,b,I
(n)
x
I,a,II
(n)
x
II,b,II
(n)
x
II,b,I
(n)
.
Its initial value is defined according to (3) by:
x(1) =
4
3
ε
ε
.
It satisfies the recursive equation (4), that is:
x
I,b,I
(n)
x
I,a,II
(n)
x
II,b,II
(n)
x
II,b,I
(n)
=
4 ε ε 4
3 ε ε 3
ε 2 2 ε
ε 6 6 ε
⊗
x
I,b,I
(n− 1)
x
I,a,II
(n− 1)
x
II,b,II
(n− 1)
x
II,b,I
(n− 1)
.
The following table contains the first values obtained
thanks to this recurrence in R
max
.
n 1 2 3 4 5 ...
x
I,b,I
(n) 4 8 13 17 22 ...
x
I,a,II
(n) 3 7 12 16 21 ...
x
II,b,II
(n) ε 5 9 14 18 ...
x
II,b,I
(n) ε 9 13 18 22 ...
For example, the possible sequences of length
3 ending with event b and leading to state I are
{bbb, bab, abb}. These strings correspond to the fol-
lowing sequences of state transitions
I
b
→ I
b
→ I
b
→ I,
I
b
→ I
a
→ II
b
→ I,
I
a
→ II
b
→ I
b
→ I.
We have σ
3,b,I
= {12,13}.
On the other hand, we have
H
b,I
= {(I,b,I),(II,b,I)},
hence
M
j∈H
b,I
[x(3)]
j
= max{x
I,b,I
(3),x
II,b,I
(3)} = max(13,13) = 13,
which corresponds to the maximum element of σ
3,b,I
.
In other words,
L
j∈H
b,I
[x(3)]
j
= 13 is the maximum
completion date for sequences of length 3 ending by
event b and leading to state I.
3.2 Representation Related to the
Optimal Case Behavior
In this section, we define a representation in a very
similar way to the previous section one, but over
(min,+) algebra instead of (max,+) algebra. The
reader must have in mind that ⊕ then represents the
min operation and ε = +∞.
We define the matrix denoted A as follows : A ∈
R
|H|×|H|
min
and for j = (p,a,q) ∈ H, k = (r,a
′
,s) ∈ H,
A
jk
=
(
[µ(a)]
pq
if s = p,
ε otherwise.
(5)
Proposition 2. Let x(n) ∈ R
|H|×1
min
, for n ∈ N be de-
fined iteratively by
x(1), with for j = (p,a,q),
[x(1)]
j
=
(
[µ(a)]
pq
if p is an initial state,
ε otherwise.
(6)
x(n) = A ⊗ x(n− 1). (7)
For all a ∈ Σ,q ∈ Q,
L
j∈H
a,q
[x(n)]
j
is a minorant for
σ
n,a,q
, that is to say, a minorant for the completion
dates of sequences of length n ending by event a and
leading to state q.
Proof 2. The proof goes along the same lines as
the proof of proposition 1 and also proceeds by
induction. According to (6), we have
L
j∈H
a,q
[x(1)]
j
=
L
{p∈Q|p initial state}
[µ(a)]
pq
= min
{p∈Q|p initial state}
[µ(a)]
pq
which minors the completion date to reach the state q
upon the occurrence of the only event a. Let us sup-
pose that for all α ∈ Σ, p ∈ Q,
L
j∈H
α,p
[x(n)]
j
is a mino-
rant of σ
n,α,p
.
The same arguments as those in the proof of proposi-
tion 1 lead to
L
j∈H
a,q
[x(n+ 1)]
j
,
=
L
p∈Q
[µ(a)]
pq
⊗
"
L
α∈Σ
L
k∈H
α,p
[x(n)]
k
#
.
= min
p∈Q
[µ(a)]
pq
⊗
"
L
α∈Σ
L
k∈H
α,p
[x(n)]
k
#
.
Since
L
α∈Σ
L
k∈H
α,p
[x(n)]
k
is a minorant for the com-
pletion dates of sequences of length n leading to state
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
508

p, we can claim that
L
j∈H
a,q
[x(n+ 1)]
j
is also a mino-
rant for the completion dates of sequences of length
n+ 1 ending by event a and leading to state q.
Example 7. Let us consider again the (max,+) au-
tomaton represented in figure 1.
Vector x(n) is written as follows:
x(n) =
x
I,b,I
(n)
x
I,a,II
(n)
x
II,b,II
(n)
x
II,b,I
(n)
.
Its initial value is defined according to(6) by:
x(1) =
4
3
ε
ε
.
It satisfies the recursive equation (7), that is:
x
I,b,I
(n)
x
I,a,II
(n)
x
II,b,II
(n)
x
II,b,I
(n)
=
4 ε ε 4
3 ε ε 3
ε 2 2 ε
ε 6 6 ε
⊗
x
I,b,I
(n− 1)
x
I,a,II
(n− 1)
x
II,b,II
(n− 1)
x
II,b,I
(n− 1)
.
The following table contains the first values obtained
thanks to this recurrence in R
min
:
n 1 2 3 4 5 ...
x
I,b,I
(n) 4 8 12 15 17 ...
x
I,a,II
(n) 3 7 11 14 16 ...
x
II,b,II
(n) ε 5 7 9 11 ...
x
II,b,I
(n) ε 9 11 13 15 ...
We mentioned in the last example that σ
3,b,I
, that
is the set of the possible completion dates for the se-
quences of length 3 ending by event b and leading to
state I, is given by
σ
3,b,I
= {12, 13},
and H
b,I
= {(I,b,I),(II,b,I)}. We then have
M
j∈H
b,I
[x(3)]
j
= min{x
I,b,I
(3)x
II,b,I
(3)} = min(12,11) = 11.
For this example,
L
j∈H
b,I
[x(3)]
j
is a minorant for σ
3,b,I
.
Let us now mention a case where the obtained mi-
norant is also the minimum element of σ
n,a,q
. The set
of the possible sequences of length 2 ending by event
b and leading to state I is: {bb, ab}.
We then have σ
2,a,I
= {8,9} .
We also have H
b,I
= {(I,b,I),(II, b,I)} and accord-
ing to the table below:
M
j∈H
b,I
[x(2)]
j
= min{x
I,b,I
(2),x
II,b,I
(2)} = min(8, 9) = 8.
The result
L
j∈H
b,I
[x(2)]
j
is not only a minorant of σ
2,b,I
(in accordance with the proposition), but it is also the
minimum element of this set.
4 CONTRIBUTIONS TO THE
PERFORMANCE
EVALUATIONS OF DES
In what follows, we highlight some performance eval-
uation elements that are provided by the representa-
tions proposed in the previous section. We only fo-
cus on maximum and minimum execution time for
a sequence of given length, which have previously
been studied in the literature on (max,+) automata
(Gaubert, 1995), (Su and Woeginger, 2011), (Gaubert
and Mairesse, 1999).
4.1 Maximum Execution Time for
Sequences of Given Length
For some systems, it is important to have knowledge
of the maximum execution time for the sequences of
given length n.
Its calculation is presented in (Gaubert, 1995) as
follows:
l
worst
n
=
L
w∈Σ
n
L
p∈Q
[x
G
(w)]
p
,
=
L
w∈Σ
n
L
p∈Q
[αµ(w
1
)...µ(w
n
)],
=
L
p∈Q
[αM
n
]
p
,
with M =
L
a∈Σ
µ(a).
Another computation method, using heap models, is
presented in (Su and Woeginger, 2011). In both cases
the algorithmic complexity is polynomial (but lower
with the second method).
The representation given in Proposition 1, allows
this indicator to be evaluated (with a polynomial com-
plexity also since it only implies multiplications of
matrices over R
max
) as:
l
worst
n
=
M
j∈H
[x(n)]
j
.
Note that it is possible to refine the indicator, by cal-
culating the maximum completion date for a sequence
of length n leading to a specific state q and ending by
a given event a:
M
j∈H
a,q
[x(n)]
j
=
M
j∈H
a,q
[A
n−1
x(1)]
j
.
4.2 Minimum Execution Time for
Sequences of Given Length
In some cases, it may be important to have the knowl-
edge of the minimum execution time for sequences of
PerformanceEvaluationofDiscreteEventSystemsThankstoNewRepresentationsfor(max,+)Automata
509

given length n. It is presented in (Gaubert, 1995) as
follows:
l
opt
n
=
M
w∈Σ
n
M
p∈Q
[x
G
(w)]
p
,
where
L
represents the min operation.
Its calculation is only presented for a reduced class
of (max,+) automata (deterministic automata), and the
algorithmic complexity is high. In (Su and Woegin-
ger, 2011), it is shown that the general case is NP-
complete.
In Proposition 2 and thanks to the new representa-
tion, we can easily approximate this indicator for all
(max,+) automata (knowing that we can sometimes
get the exact value (see example 7)), as
l
opt
n
≥
M
j∈H
[x(n)]
j
.
A refinement is also possible for specific final state
and event:
M
j∈H
a,q
[x(n)]
j
=
M
j∈H
a,q
[A
n−1
x(1)]
j
.
5 CONCLUSIONS
We have proposed new representations for (max,+)
automata. We have shown that these could be ap-
plied to performance evaluation and notably to get:
the maximum execution time for sequences of length
n and a minorant for the minimum execution time for
sequences of length n.
In future investigations, the exact algorithmic
complexity of the method should be determined and
compared with the existing methods. Spectral proper-
ties of matrices A and A should be exploited to reduce
this complexity. We also think that additional perfor-
mance indicators could be derived from the proposed
representations for (max,+) automata.
A control approach, inspired by that for logical au-
tomata presented in (Ramadge and Wonham, 1989),
has been proposed for (max,+) automata in (Komenda
et al., 2009). The proposed representations could
be used to elaborate alternative control laws. Since
the representations are similar to standard state-space
representations, we should consider to transpose the
control laws developedfor linear (max,+) and (min,+)
systems, for example in (Houssin et al., 2007) and
(Lahaye et al., 1999).
REFERENCES
Baccelli, F., Cohen, G., Olsder, G.-J., and Quadrat, J.-P.
(1992). Synchronization and Linearity. Wiley.
Cassandras, C. G. and Lafortune, S. (2008). Introduction to
discrete event systems. Springer.
Gaubert, S. (1995). Performance Evaluation of (max,+) Au-
tomata. IEEE Transaction on Automatic Control, vol.
40(12):2014–2025.
Gaubert, S. and Mairesse, J. (1999). Modeling and Analy-
sis of Timed Petri Nets using Heaps of Pieces. IEEE
Transaction on Automatic Control, vol. 44(4):683–
698.
Heidergott, B., Olsder, G. J., and Woude, J. V. D. (2006).
Max Plus at work. Princeton.
Houssin, L., Lahaye, S., and Boimond, J.-L. (2007).
Just in Time Control of Constrained (max,+)-Linear
Systems. Discrete Event Dynamic Systems, vol.
17(2):159–178.
Komenda, J., Lahaye, S., and Boimond, J.-L. (2009). Su-
pervisory Control of (max,+) Automata: A Behav-
ioral Approach. Discrete Event Dynamic Systems, vol.
19(4):525–549.
Lahaye, S., Boimond, J.-L., and Hardouin, L. (1999). Op-
timal Control of (Min,+) Linear Time-Varying Sys-
tems. In 8th International Workshop on Petri Nets
and Performance Models (PNPM 1999), pages 170–
178, Saragossa, Spain.
Ramadge, P. J. G. and Wonham, W. M. (1989). The control
of discrete event systems. Proceedings of the IEEE,
77:81–98.
Su, R. and Woeginger, G. J. (2011). String Execution Time
for Finite Languages: Max is Easy, Min is Hard. Au-
tomatica, 47(10):2326–2329.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
510
