
Inference in Hierarchical Multidimensional Space
Alexandr Savinov
SAP Research, Chemnitzerstr. 48, 01187 Dresden, Germany
Keywords: Multidimensional Data Models, Data Analytics, Concept-oriented Model, Inference, Query Languages.
Abstract: In spite of its fundamental importance, inference has not been an inherent function of multidimensional
models and analytical applications. These models are mainly aimed at numeric analysis where the notion of
inference is not well defined. In this paper we define inference using only multidimensional terms like axes
and coordinates as opposed to using logic-based approaches. We propose an inference procedure which is
based on a novel formal setting of nested partially ordered sets with operations of projection and de-
projection.
1 INTRODUCTION
Euclidean geometry is an axiomatic system which
dominated for more than 2000 years until René
Descartes revolutionized mathematics by developing
Cartesian geometry also known as analytic
geometry. The astounding success of analytical
geometry was due to its ability to reason about
geometric objects numerically which turned out to
be more practical and intuitive in comparison with
the logic-based Euclidean geometry.
The area of data modeling and analysis can also
be characterized as having two branches or patterns
of thought. The first one follows the Euclidean
axiomatic approach where data is described using
propositions, predicates, axioms, inference rules and
other formal logic constructs. For example,
deductive data models and the relational model are
based on the first-order logic where the database is
represented as a number of predicates. The second
major branch in data modeling relies on the
Cartesian conception where data is thought of as a
set of points in a multidimensional space with
properties represented as coordinates along its axes.
The multidimensional approach has been proven to
be extremely successful in analytical applications,
data warehousing and OLAP.
Although multidimensional data models have
been around for a long time (Pedersen and Jensen,
2001); (Pedersen, 2009), all of them have one
serious drawback in comparison with logic-based
models: they do not have a mechanism of inference.
Yet it is an essential function which allows for
automatically deriving relevant data in one part of
the model given constraints in another part without
the need to specify how it has to be done. For
example, if we need to retrieve a set of writers by
specifying only a set of publishers then this could be
represented by the following query:
GIVEN (Publishers WHERE name == 'XYZ')
GET(Writers)
Importantly, this query does not have any indication
of what is the schema and how Publishers are
connected with Writers.
Answering such queries especially in the case of
complex schemas is a highly non-trivial task because
multidimensional data modeling has been
traditionally aimed at numeric analysis rather than
reasoning. Currently existing solutions rely on data
semantics (Peckham and Maryanski, 1988),
inference rules in deductive databases (Ullman and
Zaniolo, 1990), and structural assumptions as it is
done in the universal relation model (URM) (Fagin
et al., 1982); (Vardi, 1988). Yet, to the best of our
knowledge, no concrete attempts to exploit
multidimensional space for inference have been
reported in the literature, apart from some
preliminary results described in (Savinov, 2006a);
(Savinov, 2006b).
In this paper we present a solution to the problem
of inference which relies on the multidimensional
structure of the database. More specifically, the
paper makes the following contributions: 1) We
introduce a novel formal setting for describing
multidimensional spaces which is based on nested
partially ordered sets. 2) We define operations of
70
Savinov A..
Inference in Hierarchical Multidimensional Space.
DOI: 10.5220/0004039000700076
In Proceedings of the International Conference on Data Technologies and Applications (DATA-2012), pages 70-76
ISBN: 978-989-8565-18-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

projection and de-projections which serve as a basis
for inference. 3) We define procedures of constraint
propagation and inference as well as describe how
they are supported by the query language.
The paper has the following layout. Section 2
describes the formal setting by defining the notion of
nested partially ordered set and how it is used to
represent hierarchical multidimensional spaces.
Section 3 defines main operations on nested posets
and how they are used for inference. Section 4
makes concluding remarks.
2 CONCEPT-ORIENTED MODEL
The approach to inference described in this paper
relies on a novel unified model, called the concept-
oriented model (COM) (Savinov, 2011a); (Savinov,
2011b); (Savinov, 2012). One of the main principles
of COM is that an element consists of two tuples:
one identity tuple and one entity tuple. These
identity-entity couples are modeled by a novel data
modeling construct, called concept (hence the name
of the model), which generalizes classes. Concept
fields are referred to as dimensions. Yet, in this
paper we will not distinguish between identities and
entities by assuming that an element is one tuple.
Figure 1: Database is a partially ordered set.
For this paper, another COM major principle is
important which postulates that a set of data
elements is a partially ordered set (poset). Another
approach where posets are used for data modeling is
described in (Raymond, 1996). In COM, posets are
represented by tuples themselves, that is, tuple
membership relation induces partial order relation
‘<’ (less than):
ee
1
,, <〉〈 KK . Here <
1
means
‘immediately less than’ relation (‘less than’ of
rank 1). If
ba < then a is referred to as a lesser
element and b is referred to as a greater element.
Thus tuple members are supposed to be immediately
greater than the tuples they are included in. And
conversely, a tuple is immediately less than any of
its member tuples it is composed of. Since tuple
membership is implemented via references (which
are identity tuples), this principle essentially means
that an element references its greater elements.
Fig. 1 is an example of a poset graphically
represented using a Hasse diagram where an element
is drawn under its immediate greater elements and is
connected with them by edges.
At the level of concepts, tuple order principle
means that dimension types specify greater concepts.
Then a set of concepts is a poset where each concept
has a number of greater concepts represented by its
dimension types and a number of lesser concepts
which use this concept in its dimensions. For
example, assume that each book has one publisher:
CONCEPTBooks//Books<Publishers
IDENTITY
CHAR(10)isbn
ENTITY
CHAR(256)title
Publisherspublisher//Greaterconcept
According to this principle, Publishers is a
greater concept because it is specified as a type
(underlined) of the dimension publisher.
The main benefit of using partial order is that it
has many semantic interpretations: attribute-value
(greater elements are values characterizing lesser
elements), containment (greater elements are sets
consisting of lesser elements), specific-general
(greater elements are more general than lesser
elements), entity-relationship (lesser elements are
relationships for greater elements), and
multidimensional (greater elements are coordinates
for lesser elements). These interpretations allow us
to use COM as a unified model.
In the context of this paper, the most important
property of partial order is that it can be used for
representing multidimensional hierarchical spaces.
The basic idea is that greater elements are
interpreted as coordinates with respect to their lesser
elements which are interpreted as points. Thus an
element is a point for its greater elements and a
coordinate for its lesser elements. In Fig. 1, e is a
point with coordinates d and f (its greater elements)
and at the same time it is a coordinate for two points
a and c (its lesser elements).
In multidimensional space, any coordinate
belongs to some axis and any point belongs to some
set. The question is how the notions of axes and sets
can be formally represented within the order-
theoretic setting. To solve this problem we assume
that a poset consists of a number of subsets, called
domains:
m
XXXO ∪∪∪
=
K
21
, 0
=
∩
ji
XX ,
ji
≠
∀
. Domains are interpreted as either sets of
coordinates (axes) or sets of points (spaces), and any
element is included in some domain:
OXe
k
⊂∈ .
InferenceinHierarchicalMultidimensionalSpace
71
Domains are also
partially ordered and represented
by tuples so that a domain is defined as a tuple
consisting of its immediate greater domains:
〉〈=
n
XXXX ,,,
21
K ,
i
XX
1
<
.
Any element participates in two structures
simultaneously: (i) it is included in some domain via
the membership relation ‘
∈
’, and (ii) it has some
greater and lesser elements via the partial order
relation ‘<’. In addition, the two structures are
connected via the type constraint:
ODe ⊂∈ ⇒ xDxe .. ∈
Here e.x is a greater element of e along dimension x
and D.x is a greater domain of D along the same
dimension x. This constraint means that an element
may take its greater elements only from the greater
domains. Such a set is referred to as a nested poset.
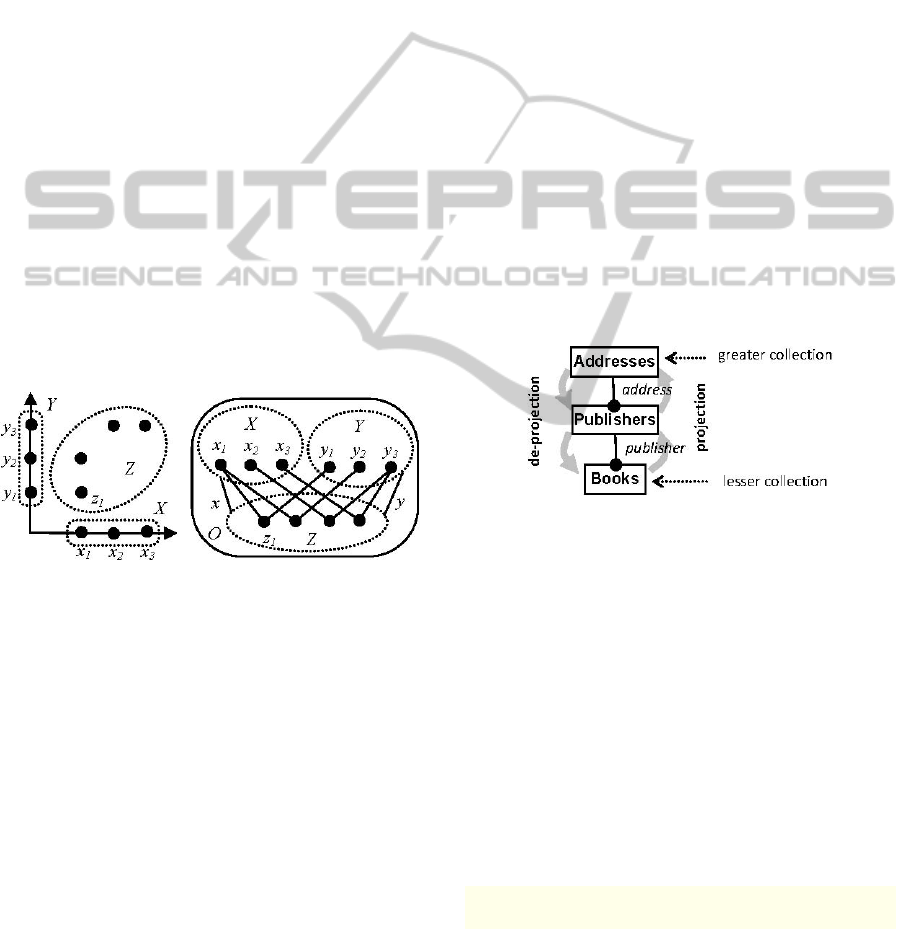
An example of a nested poset representing a 2-
dimensional space is shown in Fig. 2. This set
consists of 3 domains X, Y and Z where
〉
〈
=
YXZ ,
which means that Z has two greater domains X and
Y. Element
1
z is defined as a tuple 〉〈
11
, yx , that is,
1
x and
1
y are greater elements for
1
z . Therefore,
Zz ∈
1
is interpreted as a point while Xx
∈
1
and
Yy ∈
1
are its coordinates. According to the type
constraint, elements from Z may take their greater
elements only in X and Y.
Figure 2: Nested poset representing 2-dimensional space.
A schema is defined as a partially ordered set of
concepts where greater concepts are types of this
concept dimensions. A database schema is defined
as a partially ordered set of domains (collections)
where elements within each domain have a type of
some concept from the schema. A database is a
partially ordered set of elements each belonging to
one collection and having a number of greater
elements referenced from its dimensions.
3 INFERENCE
3.1 Projection and De-projection
Geometrically, projection of a set of points is a set of
their coordinates. De-projection is the opposite
operation which returns all points with the selected
coordinates. In terms of partial order, projection
means finding all greater elements and de-projection
means finding all lesser elements for the selected of
elements. Taking into account that greater elements
are represented by references, projection is a set of
elements referenced by the selected elements and de-
projection is a set of elements which reference the
selected elements.
To formally describe these two operation we
need to select a subset
'
Z
of points from the source
domain,
Z
Z
⊂' , and then choose some dimension x
with the destination in the target greater domain
Z
D > . Then projection, denoted as DxZ →→' ,
returns a subset of elements
DD ⊂'
which are
greater than elements from
'
Z
along dimension x:
DZzdzDdDDxZ
x
⊂∈<
∈
=
=
→→ }',|{''
Note that any element can be included in projection
only one time even if it has many lesser elements.
De-projection is the opposite operation. It returns
all points from the target lesser domain F which are
less than the elements from the source subset
'
Z
:
FZzzfFfFFxZ
x
⊂∈<
∈
=
=
←
←
}',|{''
Figure 3: Projection and de-projection in schema.
In the concept-oriented query language (COQL),
a set of elements is written in parentheses with
constraints separated by bar symbol. For example,
(Books|price<10) is a set of all cheap
books. Projection operation is denoted by right
arrow
'‐>' followed by a dimension name which is
followed by the target collection. In the database
schema, projection means moving up to the domain
of the specified dimension (Fig. 3). It returns all
(greater) elements which are referenced by the
selected elements. For example (Fig. 4), all
publishers of cheap books can be found by
projecting them up to the
Publishers collection
along the
publisher dimension:
(Books|price<10)
‐>publisher‐>(Publishers)
De-projection is the opposite operation denoted by
left arrow
'<‐'. It returns all (lesser) elements
which reference elements from the selected source
DATA2012-InternationalConferenceonDataTechnologiesandApplications
72

collection. For example, all books published by a
selected publisher can be found as follows (Fig. 4):
(Publishers|name=="XYZ")
<‐purchase<‐(Books)
Projection and de-projection operations have two
direct benefits: they eliminate the need in join and
group-by operations. Joins are not needed because
sets are connected using multidimensional
hierarchical structure of the model. Group-by is not
needed because any element is interpreted as a group
consisting of its lesser elements. Given an element
(group) we can get its members by applying de-
projection operation. For example, if it is necessary
to select only publishers with more than 10 books
then it can be done it as follows:
(Publishers|
COUNT(publisher<‐(Books))>10)
Here de-projection publisher<‐(Books)
returns all books of this publisher and then their
count is compared with 10.
Figure 4: Example of projection and de-projection.
3.2 Constraint Propagation
A query can be defined as consisting of constraints
and propagation rules. Constraints specify
conditions for selecting elements from one domain.
Propagation rules indicate how constraints imposed
on one domain are used to select elements from
another domain. For example, we can select a book
title, publishing date or price while the task is to find
all publishers which satisfy these selected values.
Since source constraints and target elements belong
to different parts of the model, propagation rules are
needed to connect them.
The main benefit of having projection and de-
projection operations is that they allow us to easily
propagate arbitrary constraints through the model by
moving up (projection) and down (de-projection).
For example, given a collection of
Books we can
find all related addresses by projecting it up to the
Addresses collection (Fig. 3):
(Books|price<10)
‐>publisher‐>(Publishers)
‐>address‐>(Addresses)
In most cases either intermediate dimensions or
collections can be omitted by allowing for more
concise queries:
(Books|price<10)
‐>publisher‐>address
(Books|price<10)
‐>(Publishers)‐>(Addresses)
De-projection allows us to move down through the
partially ordered structure of the model which is
interpreted as finding group members. For example,
given a country code we can find all related
Books
using the following query (Fig. 3):
(Addresses|country=='DE')
<‐address<‐(Publishers)
<‐publisher<‐(Books)
(Addresses|country=='DE')
<‐(Publishers)<‐(Books)
Note that such queries are very useful for nested
grouping which are rather difficult to describe using
the conventional group-by operator.
Constraint propagation can be further simplified
if instead of a concrete dimension path we specify
only source and target collections. The system then
reconstructs the propagation path itself. Such
projection and de-projection with an undefined
dimension path will be denoted by
'*‐>' and
'<‐*' (with star symbol interpreted as any
dimension path). The previous two queries can be
then rewritten as follows:
(Books|price<10)*‐>(Addresses)
(Addresses|country=='DE')<‐*(Books)
3.3 Inference
Automatically propagating constraints only up or
down is a restricted version of inference because
only more general (projection) or more specific (de-
projection) data can be derived. If source and target
collections have arbitrary positions in the schema
then this approach does not work because they do
not belong to one dimension path that can be used
for projecting or de-projecting. In the general case,
constraint propagation path consists of more than
one projection and de-projection steps. Of course,
this propagation path can be specified explicitly as
part of the query but our goal is to develop an
automatic procedure for finding related items in the
database which is called inference.
InferenceinHierarchicalMultidimensionalSpace
73

The main idea of the proposed solution is that
source and target collections have some common
lesser collection which is treated as dependency
between them. Such common lesser collections are
also used to represent relationships between their
greater collections as opposed to the explicit use of
relationships in the entity-relationship model
(Savinov, 2012). Constraints imposed on the source
collection can be used to select a subset of elements
from this lesser collection using de-projection. And
then the selected elements are used to constrain the
target elements using projection. In OLAP terms, we
impose constraints on dimension tables, propagate
them down to the fact table, and then finally use
these facts to select values from the target dimension
table. In terms of multidimensional space this
procedure means that we select points along one
axis, then de-project them to the plane by selecting a
subset of points, and finally project these points to
the target axis by using these coordinates as the
result of inference.
If X and Y are two greater collections, and Z is
their common lesser collection then the proposed
inference procedure consists of two steps:
1.
[De-projection] Source constraints
X
X
⊂' are
propagated down to the set Z using de-projection:
ZZXZ ⊂←←= *''
2.
[Projection] The constrained set
Z
Z
⊂' is
propagated up to the target set Y using projection:
YYZY ⊂→→= *''
Here by star symbol we denote an arbitrary
dimension path. In the case of n independent source
constraints
''
2
'
1
,,,
n
XXX K imposed on sets
n
XXX ,,,
21
K the de-projection step is computed as
an intersection of individual de-projections:
I
ZXZ
i
←←= *'
'
.
Figure 5: Inference via de-projection and projection.
In COQL, inference operator is denoted as
'<‐*‐>' (de-projection step followed by projection
step via an arbitrary dimension path). It connects
two collections from the database and finds elements
of the second collection which are related to the first
one. To infer the result, the system chooses their
common lesser collection and then builds de-
projection and projection dimensions paths. After
that, inference is performed by propagating source
constraints to the target along this path. For example
(Fig. 5a), given a set of young writers we can easily
find related countries by using only one operator:
(Writers|age<30)
<‐*‐>(Addresses)‐>countries
To answer this query, the system first chooses a
common lesser collection, which is
WriterBooks
in this example, and then transforms this query to
two operations of de-projection and projection:
(Writers|age<30)
<‐*(WriterBooks)//De‐project
*‐>(Addresses)‐>countries//Project
After that, the system reconstructs the complete
constraint propagation path:
(Writers|age<30)
<‐writer<‐(WriterBooks)
‐>book‐>(Books)
‐>publisher‐>(Publishers)
‐>address‐>(Addresses)‐>countries
In the case of many dependencies (common lesser
collections) or many de-projection/projection paths
between them, the system propagates constraints
using all of them. This means that all source
constraints are first propagated down along all paths
to all lesser collections using de-projection. After
that, all the results are propagated up to the target
collection using all existing dimension paths.
If the user wants to customize inference and use
only specific dimensions or collections then they can
be provided as part of the query. For example,
assume that both
Publishers and Writers have
addresses (Fig. 5b). Accordingly, there are two
alternative paths from the source to the target and
two alternative interpretations of the relationship:
writers living in some country or writers publishing
in this country. This ambiguity can be explicitly
resolved in the query by specifying the required
common collection to be used for inference:
(Addresses|country=='DE')
<‐*(WriterBooks)*‐>(Writers)
In this way, we can solve the problem of having
multiple propagation paths. In the next section we
consider the problem of having no propagation path
between source and target collections.
DATA2012-InternationalConferenceonDataTechnologiesandApplications
74

3.4 Use of Background Knowledge
If the model has a bottom collection which is less
than any other collection then inference is always
possible because it connects any pair of source and
target collections. The question is how to carry out
inference in the case the bottom collection is absent.
Formally, collections which do not have a common
lesser collection are independent, that is, their
elements are unrelated.
For example (Fig. 6), if books are being sold in
different shops then the model has two bottom
collections:
WriterBooks and Sellers. Assume
now that it is necessary to find all shops related to a
set of writers:
(Writers|age<30)<‐*‐>(Shops)
The propagation path should go through a common
lesser collection which is absent in this example and
therefore inference is not possible.
One solution to this problem is to formally
introduce a bottom collection which is equal to the
Cartesian product of its immediate greater
collections. In COQL, this operation is written as a
sequence of collections in parentheses separated by
comma:
Bottom=(WriterBooks,Sellers)
However, this artificial bottom collection (shown as
a dashed rectangle in Fig. 6) does not impose any
constraints and hence
Writers and Shops are still
independent.
Figure 6: Use of background knowledge.
To get meaningful results we have to impose
additional constraints on the bottom collection.
These constraints represent implicit dependencies
between data elements, called background
knowledge. They can be expressed via any condition
which selects a subset of elements from the bottom
collection, for instance, as a dependency between its
attributes. In our example, we assume that a written
book is the same as a sold book:
Bottom=(WriterBookswb,Sellerss|
wb.book==s.book)
Now the Bottom collection contains only a subset
of the Cartesian product of its two greater
collections and can be used for inference. We simply
specify this bottom collection as part of the query:
(Writers|age<30)
<‐*(WriterBooksbw,Sellerss|
bw.book==s.book)
*‐>(Shops)
Here the selected writers are de-projected down to
the bottom collection. Then this constrained bottom
collection is propagated up to the target. As a result,
we will get all shops selling books written by the
selected authors. Note how simple this query is
especially in comparison with its SQL equivalent
which has to contains many joins and explicit
intermediate tables. What is more important, it is
very natural because we specify what we want to get
rather than how the result set has to be built.
4 CONCLUSIONS
In this paper we have described the idea of having
inference capabilities as an inherent part of
multidimensional data models and analytical query
languages. The proposed approach is very simple
and natural in comparison to logic-based approaches
because it relies on only what is already in the
database: dimensions and data. Its main benefit is
that now inference can be made integral part of
multidimensional databases by allowing not only
doing complex numeric analysis but also performing
tasks which have always been a prerogative of logic-
based models.
REFERENCES
Fagin, R., Mendelzon, A. O. and Ullman, J. D., (1982). A
Simplified Universal Relation Assumption and Its
Properties. ACM Transactions on Database Systems
(TODS), 7(3), 343-360.
Peckham, J. and Maryanski, F., (1988). Semantic data
models. ACM Computing Surveys (CSUR), 20(3),
153–189.
Pedersen, T. B. and Jensen, C. S., (2001).
Multidimensional database technology, Computer,
34(12), 40–46.
Pedersen, T. B., (2009). Multidimensional Modeling.
Encyclopedia of Database Systems. L. Liu, M.T. Özsu
(Eds.). Springer, NY., 1777–1784.
Raymond, D., (1996). Partial order databases. Ph.D.
Thesis, University of Waterloo, Canada.
Savinov, A., (2006a). Grouping and Aggregation in the
InferenceinHierarchicalMultidimensionalSpace
75

Concept-Oriented Data Model. In Proc. 21st Annual
ACM Symposium on Applied Computing (SAC’06),
482–486.
Savinov, A., (2006b). Query by Constraint Propagation in
the Concept-Oriented Data Model. Computer Science
Journal of Moldova, 14(2), 219–238.
Savinov, A., (2011a) Concept-Oriented Query Language
for Data Modeling and Analysis, In L. Yan and Z. Ma
(Eds.), Advanced Database Query Systems:
Techniques, Applications and Technologies, IGI
Global, 85–101.
Savinov A., (2011b) Concept-Oriented Model: Extending
Objects with Identity, Hierarchies and Semantics,
Computer Science Journal of Moldova, 19(3), 254–
287.
Savinov A., (2012) Concept-Oriented Model: Classes,
Hierarchies and References Revisited, Journal of
Emerging Trends in Computing and Information
Sciences.
Ullman, J. D. and Zaniolo, C., (1990). Deductive
databases: achievements and future directions. ACM
SIGMOD Record 19(4), 75-82.
Vardi, M. Y., (1988). The Universal-Relation Data Model
for Logical Independence. IEEE Software, 5(2), 80–
85.
DATA2012-InternationalConferenceonDataTechnologiesandApplications
76
