Construction and Modeling of a Variable Collective Pitch Coaxial UAV

Jinqiang Cui

, Fei Wang

, Zhengyin Qian

, Ben M. Chen

and Tong H. Lee

NUS Graduate School for Integrative Sciences & Engineering, National University of Singapore, Singapore, Singapore

Department of Electrical & Computer Engineering, National University of Singapore, Singapore, Singapore

Keywords:

Coaxial Helicopter, Unmanned Aerial Vehicle, Flapping Dynamics, Model Identiﬁcation.

Abstract:

This paper describes the construction and modeling of a coaxial unmanned aerial vehicle for in-forest op-

eration. The bare helicopter platform is upgraded and mounted with an onboard navigation system, which

includes central processing units and sensors such as inertial measurement unit, camera and scanning laser

range ﬁnder. The model structure of the helicopter is formulated, in which the model of rotor thrust and roll-

pitch dynamics are described in details. The ﬂapping dynamics of the rotor and the stabilizer bar are presented

and lumped into a state-space model. The parameters of the state-space model are identiﬁed in frequency

domain using CIFER. Time domain veriﬁcation with a new set of ﬂight data exhibits excellent agreement with

the prediction of the identiﬁed model.

1 INTRODUCTION

With the rapid development of unmanned aerial ve-

hicles (UAVs), a wide range of platforms have been

developed. Model-scale helicopter is one of the more

popular type due to its vertical take-off and landing

capability. A single rotor UAV based on Yamaha R-

50 with a rotor diameter of 3.07 m has been devel-

oped by Carnegie Mellon Univerisity (Mettler et al.,

1999; Mettler, 2002) and the linear UAV models for

hover and cruise ﬂight have been identiﬁed. A com-

prehensive nonlinear model for a similar small-scale

single-rotor UAV has been presented by researchers

in National University of Singapore (Cai et al., 2012).

A micro coaxial indoor UAV (muFly) with a rotor di-

ameter of 0.34m has been modeled and identiﬁed by

researchers in ETH Z¨urich (Schafroth et al., 2010).

Now muFly is commercially available from Skybotix

(CoaX), which can be an ideal platform for indoor op-

eration and advanced controller design (Fankhauser

et al., 2011).

In our research scope, we intend to develop a UAV

that is capable of ﬂying through the forest. Thus the

platform has to be compact enough to ﬂy among tree

trunks. Compared to single rotor helicopters, coax-

ial helicopters produce better lift efﬁciency by avoid-

ing power losses from the tangential airﬂow. What’s

more, coaxial helicopter is also inherently more stable

than single rotor helicopters. Therefore, we choose a

coaxial helicopter as the main frame of our UAV plat-

form.

In this paper, we ﬁrst describe the mechanical

structure of the coaxial helicopter and the onboard

navigation system in section 2. In section 3, we ﬁrst

present the model structure of the coaxial helicopter,

then we derive the dual rotor thrust empirically based

on the near-hover ﬂight assumption. The ﬂapping dy-

namics of the rotor and stabilizer bar are presented

separately before they are lumped into a state-space

model. Following this, the lumped system is identi-

ﬁed in frequency domain and veriﬁed in time domain.

Section 4 concludes the paper.

2 PLATFORM DEVELOPMENT

2.1 Bare Helicopter

The ‘Kaa-350’ is a coaxial helicopter made in Ger-

many according to the design of full scale coaxial he-

licopter from the Kamov design bureau. This heli-

copter has a rotor diameter of 0.7m and weighs 990g

without battery. Its rotor head is equipped with in-

tegrated hinges and shock resistant dampers. With

the recommended conﬁguration of motor, electronic

speed controller (ESC) and blades, it can ﬂy safely

with a total weight of 2.3 kg. The mechanical struc-

ture of ‘Kaa-350’ is shown in Fig. 1. The rotor blades

are not assembled in order to better illustrate the struc-

286

Cui J., Wang F., Qian Z., Chen B. and Lee T..

Construction and Modeling of a Variable Collective Pitch Coaxial UAV.

DOI: 10.5220/0004039502860291

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 286-291

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

eadlock

roscope

per Rotor

Swashpla

LowerRo

LowerS

Moto

awContr

te

or

ashplate

r

tabilizer

ESC

ol



Figure 1: Description of bare helicopter.

ture. The helicopter consists of two contrarotating ro-

tors: the upper rotor and the lower rotor. The pitch an-

gles of the two rotors are controlled by the top swash-

plate and the lower swashplate respectively. The two

swashplates are always parallel to each other since

they are connected by three linkages which rotate with

the top swashplate. The upper rotor is equipped with a

stabilizer bar through a Bell-Hiller mixer which also

inﬂuences the cyclic pitch of the upper rotor blade.

The upper rotor and lower rotor are driven by the

same brushless DC electric motor powered by a 3-cell

lithium-polymer battery through the ESC. The rota-

tion speed of the upper rotor and the lower rotor are

thus always the same. Collective and cyclic inputs

from servos are transferred to the lower swashplate

and top swashplate simultaneously, resulting in dy-

namic movement of the helicopter in heave direction

or pitch-roll direction. The yaw direction control is

realized by changing the collective pitch of the lower

rotor.

2.2 Onboard System

The helicopter gains autonomous capability provided

that it is equipped with an onboard navigation sys-

tem. This system consists of various sensors and sig-

nal processing units. As shown in Fig. 2, the avionic

system includes sensors such as inertial measurement

unit (IMU), magnetometer,GPS, scanning laser range

ﬁnder and camera. The central processing units are

two gumstix (Overo Fire) units. One gumstix imple-

ments the autonomous control of the helicopter while

the other gumstix is responsible for processing im-

age sequences captured by the camera. Serial com-

Receiver

Control

Gumstix

2.4GHz radio

Vision Gumstix

Multiplexer

Servo Controller

IMU

GPS

Magnetometer

Tail Servo

Ground Control Station

Manual Control

WiFi

Camera

Laser

Scanner

LionHub

Headlock

Three Servos

to swashplate

Figure 2: Avionic System Conﬁguration.

munication is established between the two gumstix

units. The control gumstix also reads the outputs

of onboard sensors and generates autonomous con-

trol signals which are passed to the servo controller

and fed into the multiplexer. The multiplexer has two

4-channel input ports and one 4-channel output port.

Manual control signals from the pilot are transmitted

to the receiver via 2.4GHz radio and fed into the mul-

tiplexer. The outputs of multiplexer are connected to

the three servos controlling the swashplates and the

headlock gyro mixer. The headlock gyro mixer mixes

the yaw control signal and the output of the headlock

gyroscope to generate a composite yaw control signal

that controls the yaw servo. The multiplexer is in-

dispensable since the helicopter may encounter unex-

pected situations during ﬂight where an instant switch

to manual control is required to save the helicopter.

During manual ﬂight or autonomous ﬂight, helicopter

states and sensor outputs are logged online and crit-

ical information are transferred to ground station via

WiFi communication. Control command from ground

station could also be transmitted to the helicopter in

autonomous ﬂight mode. Fig. 3 shows the completed

UAV platform operating in the air.

Figure 3: Helicopter ﬂying in the air.

ConstructionandModelingofaVariableCollectivePitchCoaxialUAV

287



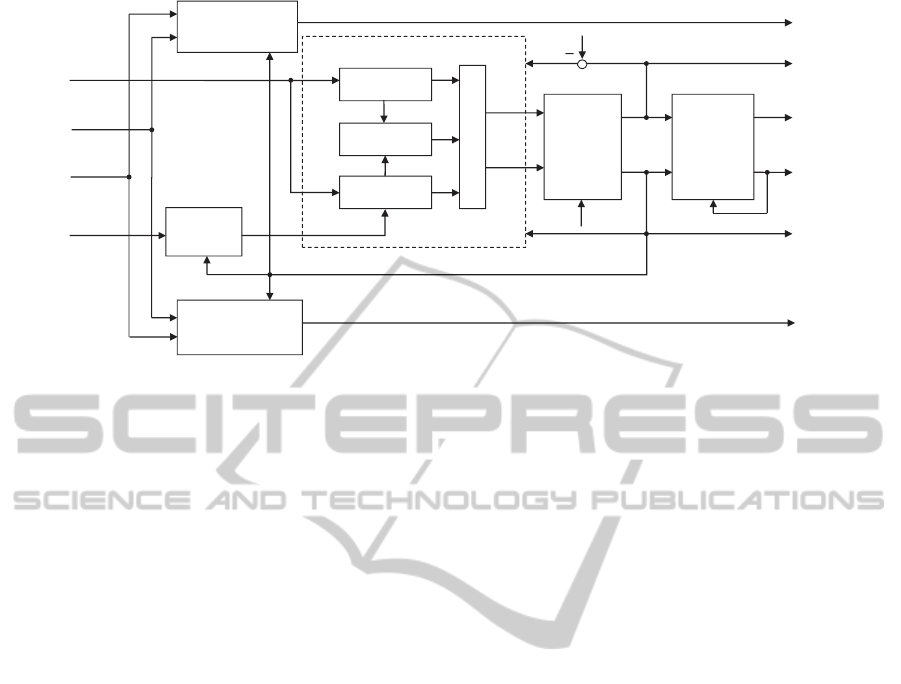
Headlock

controller

Lowerrotor

flappingdynamics

Upperrotor

Fuselage

Lowerrotor

6ͲDOF

rigidͲbody

dynamics

ForcesandMoments

b

Kinematics

߶ǡ ߠǡ ߰

wind

ݔǡ ݕǡ ݖ

ݑǡ ݒǡ ݓ

ௗ௪

ǡ ܾ

ௗ௪

݌ǡ ݍǡ ݎ 

௖௢௟



௟௔௧



௟௢௡



௣௘ௗ



௨௣

ǡ ܾ

௨௣



௣௘ௗ



Upperrotor

flappingdynamics



Figure 4: Model Structure Overview.

3 MODELING AND PARAMETER

IDENTIFICATION

3.1 Model Structure

The UAV model structure is shown in Fig. 4. The col-

lective input δ

col

controls the collective pitch angles

of both upper and lower rotors through the two paral-

lel swashplates. The cyclic inputs δ

lat

and δ

lon

tilt the

upper and lower swashplates and generate ﬂapping

motion for both rotors, causing the longitudinal and

lateral movements of the helicopter. The yaw chan-

nel control δ

ped

is ﬁrst mixed with the output of the

headlock gyro (PI controller) before it is applied on

the collective pitch of the lower rotor. The model is

denoted in a compact form as follows,

x = f(x,u,w) , (1)

where

x = (

x y z u v w φ θ ψ· ··

·· · p q r a

)

u = (

lat

lon

col

ped

)

w = (

)

x is the state vector, u is the input vector, δ

col

, δ

lat

lon

and δ

ped

are the collective, lateral, longitudinal

and pedal inputs to the whole system. w

stands for

the wind disturbance velocity. The overall dynamics

of the helicopter could be separated into three sub-

systems: the roll-pitch dynamics, the yaw dynamics

and the heave dynamics. The roll-pitch dynamics,

capturing the angular responses of helicopter to the

cyclic inputs, constitutes the core of helicopter dy-

namics (Mettler et al., 1999). Thus we mainly present

our results in the modeling and identiﬁcation of the

roll-pitch dynamics in this paper.

3.2 Thrust Formulation

It is a very complex issue to address the coaxial rotor

aerodynamics. A comprehensive survey (Coleman,

1997) has covered the major aerodynamic experi-

ments and computational models dealing with coax-

ial rotor systems. It covered issues of separation dis-

tance, load sharing between rotors, wake structure,

solidity effects, swirl recovery, and the effects of hav-

ing no tail rotor. (Lim et al., 2009) investigated the

ground and rotor spacing effects and Reynolds num-

ber scaling effect by comparing three rotor conﬁgu-

rations, concluding that the coaxial rotor spacing ef-

fect on hover performance was minimal for the rotor

spacing larger than 20% of the rotor diameter. Re-

searchers (Kim and Brown, 2008; Kim and Brown,

2006) at Glasgow University has developed a Vor-

ticity Transport Model (VTM) to study the aerody-

namics of coaxial rotor systems. They stated that the

state-of-the-art computational modeling of helicopter

aerodynamics had managed to model the interactive

aerodynamic ﬂow ﬁeld associated with a coaxial ro-

tor system.

Since the designed UAV will work at near-hover

condition, we decide to ﬁrst extract an empirical rela-

tionship between dual rotor thrust T

and collective

input δ

col

. A test bench is utilized to facilitate a series

of tests where the dual rotor thrust and collectiveinput

are recorded simultaneously. Fig. 5 shows the results

of ﬁve tests performed on two fully charged batteries.

After ﬁtting the results using the least square method

and averaging the ﬁve groups of coefﬁcients, a linear

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

288

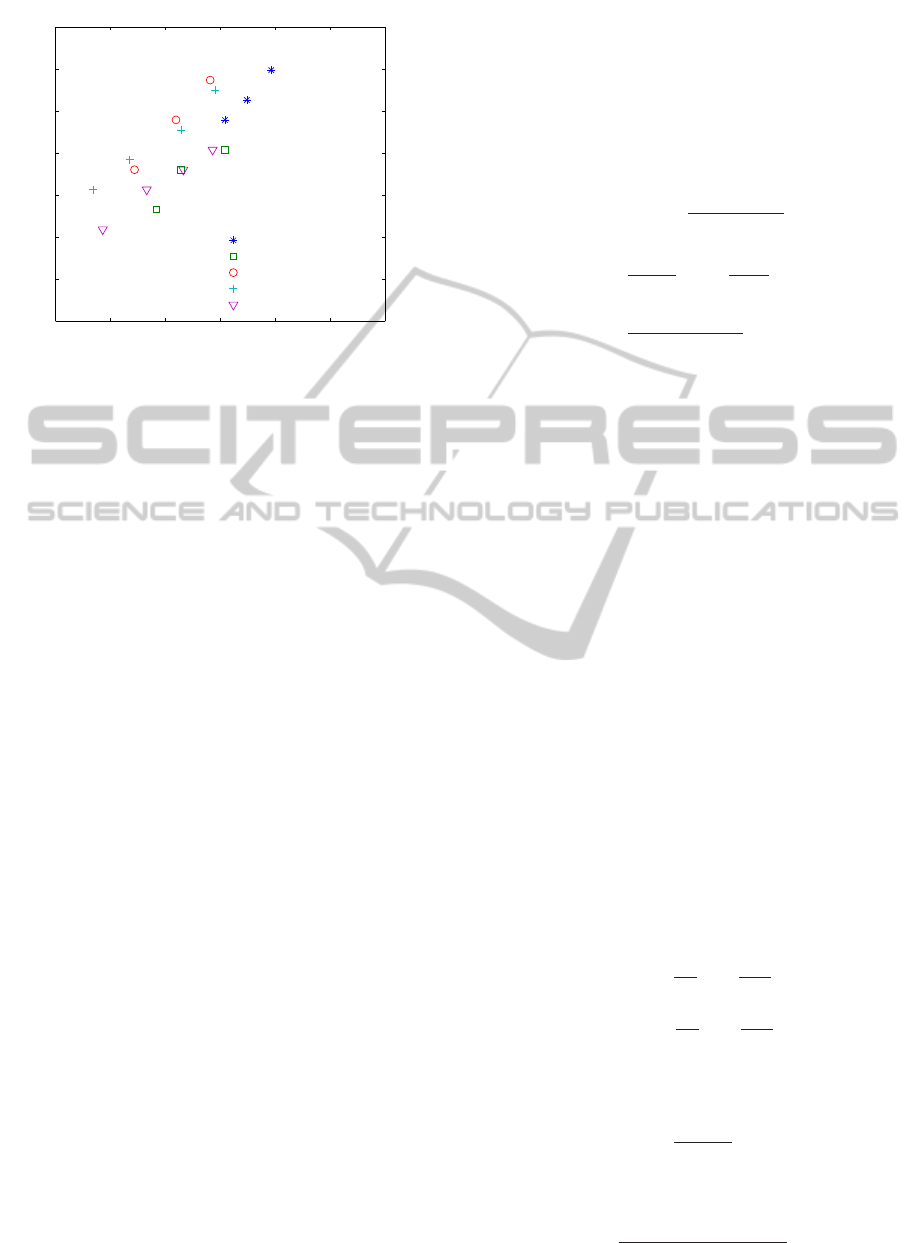
−0.25 −0.2 −0.15 −0.1 −0.05 0 0.05

17.5

18.5

19.5

20.5

col

(−1,1)

Force(N)

Dual Rotor Force vs Collective Input

Test 1 with battery 1

Test 2 with battery 1

Test 1 with battery 2

Test 2 with battery 2

Test 3 with battery 2

Figure 5: Thrust of dual rotor against collective input.

relationship is obtained as:

= K

col

+ T

, (2)

where K

= 10.09N and T

= 20.812N.

For near-hover ﬂight, the direction of the rotor

thrust can be assumed to remain perpendicular to the

rotor tip-path-plane. The projections of main rotor

thrust on the helicopter body axes are deﬁned as:

= −T

sina

, (3)

= T

sinb

, (4)

= −T

cosa

cosb

. (5)

The moments generated by the main rotor are:

= (K

+ T

) sin(b

), (6)

= (K

+ T

) sin(a

), (7)

where K

is the spring constant, H

is the distance

from center of gravity (CG) to the middle of two ro-

tor planes, a

and b

are the equivalent longitudinal

and lateral ﬂapping angles respectively. The torques

from upper rotor and lower rotor are balanced when

no heading change is required.

3.3 Flapping Dynamics

3.3.1 Bare Rotor Flapping Dynamics

One way to represent the rotor dynamics is to regard

it as a rigid disc which can tilt about the longitudi-

nal and lateral axes. Detail description of the rotor

equations are extremely complicated. Here, a sim-

pliﬁed formulation is adopted, where the rotor forces

and moments are expressed as a polynomial function

of the rotor state variables (Mettler, 2002). Moreover,

by removing the higher order terms of the Tip-Path-

Plane (TPP) equation, the remaining ﬁrst-order rotor

dynamics could be expressed as:

= −b

− τ

p+ B

+ θ

cyc,bi

, (8)

˙a

= −a

− τ

q+ A

+ θ

cyc,ai

, (9)

where

= −B

Ω

β,mr

, (10)

Ω



1−



−1

, (11)

ρc

lα,mr

β,mr

. (12)

and b

(i represents { up, dw}) are the ﬁrst-order

TPP ﬂapping angles in the longitudinal and lateral

directions for upper and lower rotors. τ

and γ

are

the ﬂapping time constant and the lock number of the

rotor blades respectively, I

β,mr

is the blade moment

of inertia. θ

cyc,a

and θ

cyc,b

are the longitudinal and

lateral cyclic pitch of rotor blade. The approximate

formulation in Eq.(8-9) characterizes the crucial TPP

responses with respect to cyclic control inputs and he-

licopter motion.

3.3.2 Stabilizer Bar Flapping Dynamics

The stabilizer bar, which is attached to the upper main

rotor shaft via a free-teetering hinge, can be regarded

as a secondary rotor. It consists of two paddles and

a steel rod. The stabilizer bar is not designed to pro-

duce thrust or moment on the main hub, whereas its

main function is to adjust the helicopter dynamics via

the Bell-Hiller mixer by augmenting the cyclic pitch

command of the upper rotor. It serves as a feed-

back system which increases the helicopter robustness

against wind gust and turbulence (Cai et al., 2011).

The ﬂapping dynamics of stabilizer bar can be ex-

pressed as two ﬁrst-order differential equations:

˙c

= −q −

lon

, (13)

= −p−

lat

, (14)

where τ

is the stabilizer bar ﬂapping time constant,

and it can be calculated as

Ω

, (15)

where γ

is the stabilizer bar Lock number:

ρc

lα,sb



− r



β,sb

. (16)

ConstructionandModelingofaVariableCollectivePitchCoaxialUAV

289

The free-teetering hinge does not constrain the ﬂap-

ping of stabilizer bar, thus there is no coupling be-

tween the longitudinal and lateral ﬂapping motions.

The augmented rotor cyclic pitch of upper rotor can

be expressed as

cyc,aup

= A

lon

+ K

, (17)

cyc,bup

= B

lat

+ K

, (18)

where K

is the ratio of rotor blade cyclic pitch to

stabilizer bar ﬂapping.

3.3.3 Lumped Flapping Dynamics

In this coaxial helicopter conﬁguration, the upper ro-

tor and the lower rotor receive the same cyclic input

(δ

lon

,δ

lat

) since the top swashplate and bottom swash-

plate are always parallel. To minimize the overall

complexity of the model, the two counter rotating ro-

tor discs are treated as one equivalent rotor disc with

respect to ﬂapping motions. Thus there exists only

two equivalent ﬂapping angles (a

, b

). This assump-

tion produces accurate results which are shown in sec-

tion 3.3.4. Combining Eq. 8-18, the lumped ﬂapping

dynamics subsystem could be represented in the fol-

lowing state space model:

x = A x+ B u, (19)

y = C x, (20)

where

A =







0 0 0 L

0 0 M

0 −1 −

−1 0

−







, (21)

B =







0 0

0 A

′

lon

′

lat







, (22)

C =



1 0 0 0

0 1 0 0



, (23)

x =













, u =



lat

(t − τ

lat

)

lon

(t − τ

lon

)



, y =





, (24)

mgH

+ K

, M

mgH

+ K

. (25)

The rotor spring constant K

, the lateral and longi-

tudinal control derivatives B

′

lat

, A

′

lon

, the lateral and

longitudinal control delay τ

lat

, τ

lon

, and the equiva-

lent ﬂapping time constant τ are to be identiﬁed via

frequency domain identiﬁcation in section 3.3.4. The

coupling term A

and B

are neglected.

3.3.4 Roll-Pitch Dynamics Identiﬁcation

The ﬂapping dynamics identiﬁcation makes full use

of a toolkit called CIFER developed by the U.S.

Army and NASA speciﬁcally for rotorcraft applica-

tions (Mettler et al., 1999). It incorporates a range of

utilities to support the various steps of the identiﬁca-

tion process. Flight tests featuring frequency-sweep

input in the longitudinal and lateral directions are per-

formed multiple times. During the ﬂights, the control

inputs and the helicopter angular rates are recorded

online with a sampling rate of 50Hz. CIFER identi-

ﬁes the model parameters by searching for the best-

ﬁt parameters to match frequency responses between

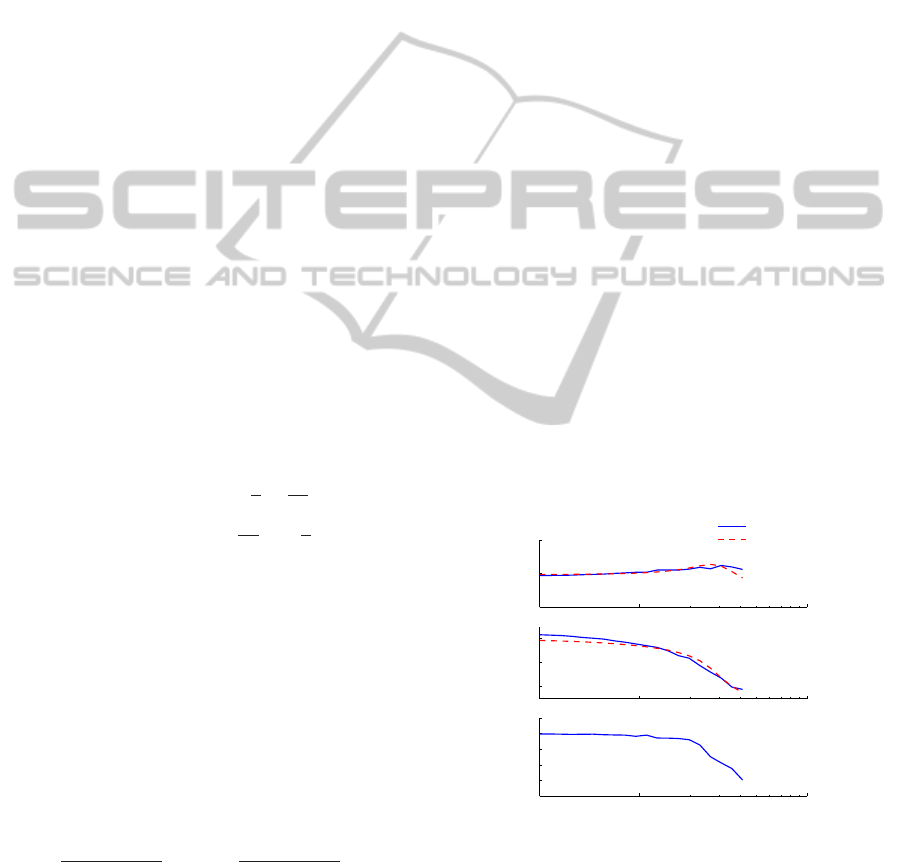
the ﬂight test data and the hypothetic model. Fig. 6

shows the on-axis pitch angular rate response with re-

spect to longitudinal input. The coherence level re-

mains above 0.6 up to 30 rad/s. This good coherence

indicates the good linearity of the helicopter in hover

ﬂight (Tischler and Remple, 2006). Time domain ver-

iﬁcation is also performed with another ﬂight test data

which is not used in the identiﬁcation process. Fig.7

shows excellent agreement between the model simu-

lation and the ﬂight data in both longitudinal direc-

tion. The same process is applied to the lateral direc-

tion where the roll dynamics is identiﬁed in frequency

domain and veriﬁed in time domain. Table. 1 lists the

values of the identiﬁed parameters together with their

Cramer-Rao percent and insensitivity. The Cramer-

Rao percent and insensitivity are less than 15% and

5% respectively, indicating the high accuracy of the

identiﬁed parameter.

−20

Magnitude (DB)

lon

−− q

Experiment

Simulation

−200

−100

Phase (deg)

0.2

0.4

0.6

0.8

1.2

Coherence

Frequency(Rad/Sec)

Figure 6: Comparison of frequency response from longitu-

dinal input to pitch angular rate.

4 CONCLUSIONS AND FUTURE

WORK

In this paper we have presented our current progress

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

290

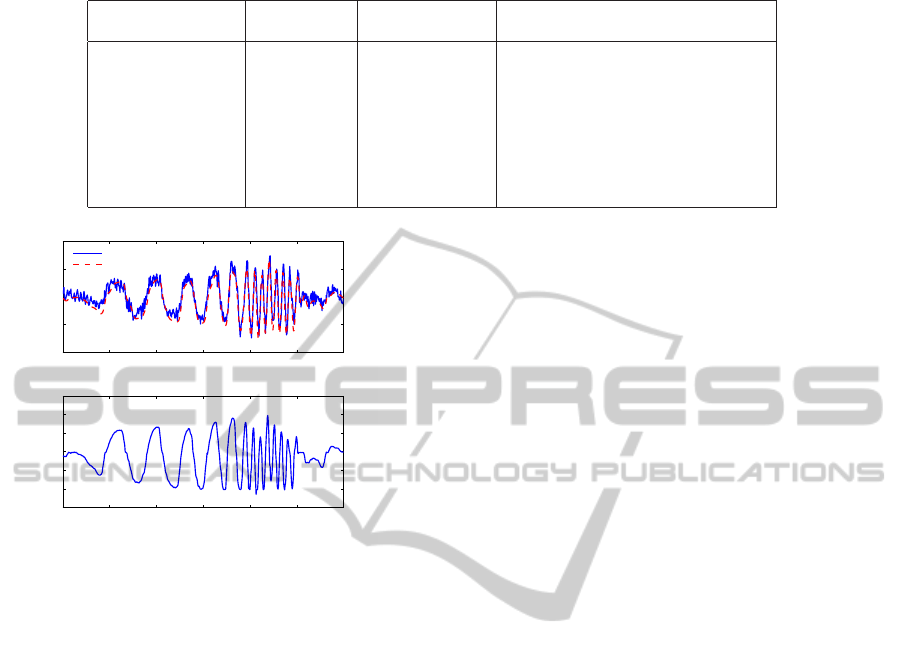
Table 1: Parameters identiﬁed from CIFER.

Parameter

Cramer-Rao

Insensitivity(%) Physical meaning

Percent(%)

= 675.8s

−2

7.171 2.433 Lateral rotor spring derivative

= 794.7s

−2

7.525 2.589 Longitudinal rotor spring derivative

τ = 0.068s 9.301 3.537 Equivalent ﬂapping time constant

′

lon

= 0.898rad/s 4.152 1.962 Longitudinal control derivative

′

lat

= 1.069rad/s 4.157 1.935 Lateral control derivative

lat

= 0.03355s 12.08 4.477 Lateral control delay

lon

= 0.03390s 12.17 4.440 Longitudinal control delay

= 11.5029Nm NA NA Rotor spring constant

0 2 4 6 8 10 12

−2

−1

q (rad/s)

Experiment

Simulation

0 2 4 6 8 10 12

−1.5

−1

−0.5

0.5

1.5

Time(s)

lon

Figure 7: Time domain veriﬁcation of longitudinal input to

pitch angular rate.

regarding the development and modeling of a coaxial

UAV platform. For platform construction, the payload

capability of the bare coaxial helicopter is guaranteed

by careful selection of the key components such as

motor, blade and ESC. The onboard avionic system

is designed and assembled onto the helicopter frame

using mechanical dampers. For modeling of the heli-

copter, the model structure of the platform has been

laid out. The coaxial rotor thrust has been empir-

ically derived. More importantly, the roll-pitch dy-

namics of the helicopter are formulated. Through fre-

quency domain identiﬁcation in CIFER, the equiva-

lent ﬂapping time constant and spring constant are

ﬁne-tuned. Time domain veriﬁcation using a new set

of test data has validated the ﬁdelity of the identi-

ﬁed roll-pitch dynamics. Future research work will

focus on the modeling of heave dynamics and yaw

dynamics which will produce a complete model. Ad-

ditional effort will be made to study the coaxial rotor

wake structure so that an optimal coaxial conﬁgura-

tion could be achieved.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. Feng Lin and Dr.

Guowei Cai from NUS Temasek Laboratories for the

constructive discussion and genuine help. We would

also like to thank ‘Temasek Defence Systems Insti-

tute’ for funding the project.

REFERENCES

Cai, G., Chen, B. M., and Lee, T. H. (2011). Unmanned

Rotorcraft Systems. Springer, London.

Cai, G., Chen, B. M., Lee, T. H., and Lum, K.-Y. (2012).

Comprehensive nonlinear modeling of a miniature un-

manned helicopter. Journal of the American Heli-

copter Society, 57(1):1–13.

Coleman, C. P. (1997). A survey of theoretical and experi-

mental coaxial rotor aerodynamic research. Technical

report, NASA Ames Research Center.

Fankhauser, P., Bouabdallah, S., Leutenegger, S., and Sieg-

wart, R. (2011). Modeling and decoupling control of

the coax micro helicopter. In Proc. of the IEEE/RSJ

International Conference on Intelligent Robots and

Systems (IROS).

Kim, H. and Brown, R. (2006). Coaxial rotor performance

and wake dynamics in steady and manoeuvring ﬂight.

In American Helicopter Society 62nd Annual Forum

Proceedings, volume 62, page 20.

Kim, H. and Brown, R. (2008). Modelling the aerodynam-

ics of coaxial helicopters–from an isolated rotor to a

complete aircraft. In Proceedings of the EU-Korea

Conference on Science and Technology, pages 45–59.

Lim, J. W., McAlister, K. W., and Johnson, W. (2009).

Hover performance correlation for full-scale and

model-scale coaxial rotors. Journal of the American

Helicopter Society.

Mettler, B. (2002). Identiﬁcation Modeling and Charac-

teristics of Miniature Rotorcraft. Kluwer Academic

Publisher, Nowell, MA.

Mettler, B., Tischler, M. B., and Kanade, T. (1999). System

identiﬁcation of small-size unmanned helicopter dy-

namics. In American Helicopter Society 55th Annual

Forum Proceedings, volume 2, pages 1706–1717.

Schafroth, D., Bermes, C., Bouabdallah, S., and Siegwart,

R. (2010). Modeling and system identiﬁcation of

the muﬂy micro helicopter. Journal of intelligent &

robotic systems, 57(1):27–47.

Tischler, M. and Remple, R. (2006). Aircraft and rotor-

craft system identiﬁcation: Engineering Methods with

Flight Test Examples. AIAA.

ConstructionandModelingofaVariableCollectivePitchCoaxialUAV

291