Global Optimal Solution to SLAM Problem with Unknown Initial
Estimates
Usman Qayyum and Jonghyuk Kim
School of Engineering, Australian National University, Canberra, ACT 0200, Australia
Keywords:
Greedy Random Adaptive Search Procedure, Gauss-Newton Optimization, Optimal Solution, Map-joining.
Abstract:
The paper presents a practical approach for finding the globally optimal solution to SLAM. Traditional meth-
ods are based upon local optimization based strategies and are highly susceptible to local minima due to
non-convex nature of the SLAM problem. We employed the nonlinear global optimization based approach to
SLAM by exploiting the theoretical limit on the numbers of local minima. Our work is not reliant on good
initial guess, whereas existing approaches in SLAM literature assume good starting point to avoid local min-
ima problem. The paper presents experimental results on different datasets to validate the robustness of the
approach, finding the global basin of attraction with unknown initial guess.
1 INTRODUCTION
Simultaneous Localization and Mapping (SLAM)
has drawn significant interests in robotics commu-
nities, as it enables the robotic vehicles to be de-
ployed in a fully autonomous way for various applica-
tions. SLAM literature is mostly categorized into two
main streams: Filtering based (Bailey and Durrant-
Whyte, 2006) and Maximum likelihood based (Lu
and Milios, 1997) approaches. The first stream con-
sists of Extended Kalman filter and Information filter
(S. Huang and Dissanayake, 2008) which requires lin-
earization of process and measurement models with a
cost of potential divergence and inconsistency. Fast-
SLAM (A. Doucet and Russel, 2002) is based upon
factorization of posterior but, due to limited numbers
of particles, it is unable to represent the trajectory pos-
terior in the long run.
In graph-based SLAM approaches measurements
acquired during robot motions are modeled as con-
straints. The goal of these approaches is to esti-
mate the configuration of parameters that maximally
explain a set of measurements affected by Gaussian
noise (minimizes the nonlinear least square error).
The pioneering work in graph-based SLAM is by
(Lu and Milios, 1997) in which brute force tech-
nique for range scan alignment was proposed. With
the assumption of known rotation (T. Duckett and
Shapiro, 2002) introduced a Gauss-Seidel relaxation.
The work was improved by (U. Frese and Duckett,
2005) solving a network at different level of resolu-
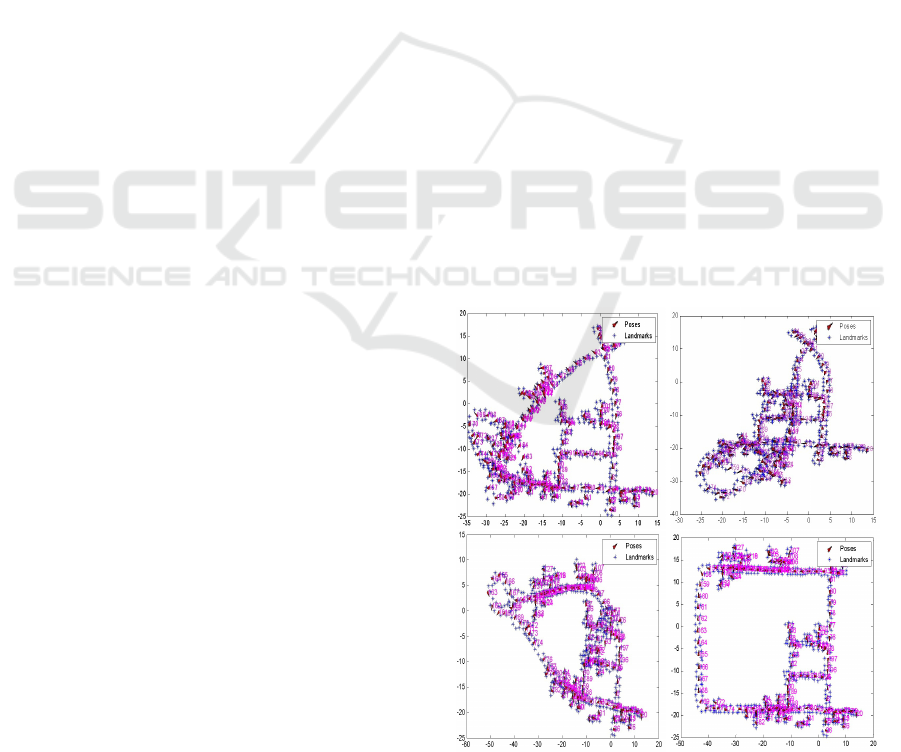
Figure 1: Examples of local solution for DLR dataset
(J. Kurlbaum, 2010) with different random initial guess.
tion. (Dellaert and Kaess, 2006) came up with QR
factorization of information matrix to solve the full
SLAM problem.
(E. Olson and Teller, 2006) uses stochastic gra-
dient descent (SGD) algorithm (E. Olson and Teller,
2006) to solve the pose only SLAM problem by ad-
dressing each constraint individually and surprises
many researcher as the algorithm can converge to the
correct solution with poor initial values. Recent re-
76
Qayyum U. and Kim J..
Global Optimal Solution to SLAM Problem with Unknown Initial Estimates.
DOI: 10.5220/0004040100760083
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 76-83
ISBN: 978-989-8565-21-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 2: SLAM is recasted as a map-joining problem: One is a growing global map (navigation coordinate with solid
lines) and the other is a new local map L (represented with ellipses). The dashed lines indicate the odometry and feature
observations.
search (R. Kummerle and Burgard, 2011) has focused
on making these algorithms more efficient and ro-
bust showing that its online implementation is feasi-
ble. Although these approaches perform efficiently in
practice, very little attention has been paid on the con-
vergence condition and none of them can guarantee a
global minimum over different initial guesses. Fig.
1 shows the results of a Gauss-Newton approach on
publicly available dataset (J. Kurlbaum, 2010) with
different random initial guesses, resulting in different
local solutions.
Global optimal solutions to highly nonlinear prob-
lems has been shown to NP-hard (Freund and Jarr,
2001). In structure from motion research, the guar-
anteed global optimal solution is investigated with
known rotation framework for L
∞
(K. Astrom and
Hartley., 2007) and branch and bound based ap-
proaches (C. Olsson and Oskarsson, 2008) whereas
in our work no such assumption of known rotation
is considered (typically the nonlinearity in measure-
ments of mobile robot applications is due to robot
orientation). In recent work (Iser and Wahl, 2010)
proposed a swarm optimization based approach to es-
timate (almost) optimal maps. Their work is based
upon meta-heuristic optimization approach which is
similar to our work but they present map as a tree of
fragments/maps with particle filtered based sampling
approach and finally conducted an ant colony search
to obtain (almost) optimal solution.
In this paper we provide an approach to get global
optimal solution for SLAM problem, which has never
been proposed before to the best of author’s knowl-
edge. Feature based SLAM problem is decomposed
as a problem of joining submaps. Necessary and suf-
ficient condition for the existence of at most two lo-
cal optimal (S. Huang and Dissanayake, 2012) is ex-
ploited by a meta-heuristic approach called GRASP
(greedy randomized adaptive search procedure) (Re-
sende and Ribeiro., 2003) which is combinatorial op-
timization to obtain global optimal solution. Meta-
heuristic approaches optimize by iteratively refining
the candidate solution by combining randomness with
local search methods (C.Blum and A.Roli, 2003).
Unknown landmark positions and vehicle pose are
considered as initial guess in a planar environment
(3DOF case).
The outline of this paper is as follows: Section 2
and 3 will provide nonlinear least square formulation
and number of local minima in SLAM problem. Sec-
tion 4 and 5 will provide detailed discussions on non-
linear global optimization based approach and greedy
search strategy. Section 6 will briefly explain global
optimal approach to map-joining. Results and discus-
sions will be presented in Section 7 followed by Con-
clusion.
2 NONLINEAR LEAST SQUARE
FORMULATION
The dimension of the SLAM problem is very high
when it is formulated as a nonlinear least square
(K. Ni, 2007) because all vehicle poses and feature
locations are considered as parameters to be deter-
mined. The decomposition of SLAM problem into
submaps not only helps to reduce the computational
complexity but also helps to improve consistency by
decreasing the nonlinearity of the system (S. Huang
GlobalOptimalSolutiontoSLAMProblemwithUnknownInitialEstimates
77

and Dissanayake, 2008; S. Huang and Frese, 2008).
The assumption we undertake in this research is that,
every SLAM problem can be decomposed into lo-
cal maps and then solved for global optimal solution.
The relative relation of local maps has fluid behav-
ior whereas the internal structure of each local map is
well known and can be optimized independently with
respect to local coordinate (K. Ni, 2007). The nonlin-
ear least square formulation for local map joining is
to minimize an objective function as follows:
F(x) = arg min
x
∑
(||E
p
||
2
U
+ ||E
f
||
2
V
), (1)
where the state vector is x =
{
X,M
}
with X being the
poses (position and orientation) of local maps and M
the features positions in absolute coordinate frame. U
and V are corresponding covariance matrices of pose
and feature observations respectively. The poses are
composed of
{
p
1
,ϕ
1
,.. . , p
t
,ϕ
t
}
where the end pose
of each local map is the start pose of next local map.
The N map features are defined as M =
{
f
1
,.. . , f
N
}
.
SLAM recasted as a map-joining problem is shown in
Fig. 2.
Let there be a local map l defined as X
l
=
p
l
,ϕ
l
with n features M
l
=
f
l
1
... , f
l
n
present in the local
coordinate frame. The local map pose X
l
is the obser-
vation of relative pose of p
l
,ϕ
l
from the global state
vector X pose p
l−1
,ϕ
l−1
as
E
p
= X
l
− H
odo
(X), (2)
and the observation model for odometry is defined as
H
odo
(X) =
R(ϕ
l−1
)
T
(p
l
− p
l−1
)
ϕ
l−1
− ϕ
l
. (3)
The SO(2) rotation matrix is defined as
R(ϕ) =
cos(ϕ) − sin(ϕ)
sin(ϕ) cos(ϕ)
. (4)
The feature positions M
l
=
f
l
1
... , f
l
n
in local map l
are observation of relative position of features and are
related (assumed data association) to global state vec-
tor. The relative feature position error E
f
is defined
as
E
f
= M
l
− H
f eat
(X,M), (5)
whereas the observation model for relative position of
features is a function of M and X
H
f eat
(X,M) =
R(ϕ
l−1
)
T
( f
l1
− p
l−1
)
...
R(ϕ
l−1
)
T
( f
ln
− p
l−1
)
. (6)
The Mahalanobis distance for both relative errors in
the cost function with zero-mean Gaussian noise with
covariance U,V can be written as
F(x) =
∑
(X
l
− H
odo
(X))
T
U
−1
(X
l
− H
odo
(X)) + (7)
∑
(M
l
− H
f eat
(X,M))
T
V
−1
(M
l
− H
f eat
(X,M)).
The measurement and process models are both
nonlinear functions, and thus the nonlinear objective
function is linearized multiple times to reach local
minima. Generally local approaches solve the objec-
tive function F(x) as
F(x + δx) = F(x) + Jδx, (8)
where J = ∂F(x)/∂(x). Let ϖ = (F(x + δx) − F(x)),
then it becomes
Jδx = ϖ, (9)
The solution can be found using pseudo-inverse of J
J
T
Jδx = J
T
ϖ
δx = (J
T
J)
−1
J
T
ϖ (10)
By including the covariance estimates (U,V ) as ξ, eq.
10 becomes
δx = (J
T
ξ
−1
J)
−1
(J
T
ξ
−1
)ϖ. (11)
When the eq. 11 is solved only ones by an optimiza-
tion based approach i.e. (Dellaert and Kaess, 2006), it
yields a similar result like the EKF or Extended infor-
mation filter (Bailey and Durrant-Whyte, 2006). The
advantage in optimization based approach comes with
repeatability of solution for eq. 11 with different lin-
earization points.
3 NUMBER OF LOCAL MINIMA
IN MAP JOINING SLAM
The SLAM formulation as linearized version of non-
linear objective function assumes local convexity, that
is with a reasonable initial estimate (near the global
basin of attraction), the algorithm will converge to
global minima. SLAM is an incremental process and
at each step, small number of new parameters need to
be estimated. However when the odometry and fea-
ture observation are not consistent with each other,
then the local optimizer can struck in local minima.
A close lookup at the observation model in equa-
tion 3 and 6 reveals that nonlinearity is only due to ori-
entation. Recently (S. Huang and Dissanayake, 2012)
provides a theoretical bound on local minima in map-
joining SLAM problem, by deriving a nonlinear equa-
tion depending only on orientation error under the as-
sumption that covariance matrices are spherical ma-
trices. The research findings in their work suggest
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
78

Figure 3: 1D problem with 2 local minima revealing possible feasible solutions from local optimization.
at most two and at least one local minima can occur.
The approach, proposed in this paper, exploits the up-
per theoretical bound under noisy observations to ob-
tain global minima by a meta-heuristic approach (dis-
cussed in following section) hence obtaining a global
optimal solution.
4 GREEDY RANDOM ADAPTIVE
SEARCH PROCEDURE
GRASP is a multi-start meta-heuristic approach to
solve combinatorial problems (Resende and Ribeiro.,
2003). Previously, it has been successfully deployed
in traveling sales man problem and firstly proposed
here for SLAM problem. GRASP basically consist of
two phases: local search and feasible solution con-
struction. The construction phase builds a feasible
solutions (using greedy approach), whose neighbor-
hood is searched by a local search phase to find local
optima. By using different feasible solutions as start-
ing points for local search in a multi-start procedure
will usually lead to good, though, most often, subop-
timal solutions. While in our problem at worst case,
we encountered two local minima when joining two
local maps, so the upper bound is searched by multi-
start until global optimal solution is returned, which
is the optimal solution.
The pseudo code in algorithm 1, details the work-
ing of GRASP approach, where local search is per-
formed by the gauss-newton formulation of eq.11.
5 RANDOMIZED GREEDY
ALGORITHM
We proposed long-term memory based greedy algo-
rithm to determine a feasible solution. Fig. 3 (left)
details a simple example on 1D in which at most two
local minima are considered.The two feasible solu-
tions (x
1
,x
2
) are generated by GRASP approach and
among them two minima are found whereas x
1
reveals
the global optimal solution x
∗
.
Algorithm 1: GRASP-Algorithm: Determination of Opti-
mal Solution.
inputs : observations =
X
l
,M
l
,x =
{
pose,landmark
}
x
∗
=
{
EMPTY
}
while two local minima or max iteration are not reached
do
x ← RandomizedGreedyAlgo(.) → Algo2
x ← LocalSearch(x,observations)
if (f(x) < f(x*)) then
x
∗
= x
end if
end while
return x
∗
The generation of feasible solution is the key to
obtain the optimal solution, in timely manner from
a high dimensional search space of parameters. Fig.
3 (right) describes a search space reduction mecha-
nism in which the initial guess x
1
is first hypothe-
sized, which determines a local optimal x
∗
(the inter-
mediate traversal solution of the local optimizer are
stored in long-term memory for search space x
1
to
x
∗
). The next hypothesis of initial guess is being made
by greedy algorithm in consideration with the already
traversed solution space in long-term memory (the
goal is to avoid making an initial guess from already
traversed space). The selection of new initial guess
is based upon absolute distance criteria (greedy ap-
proach), in which the new initial guess for local opti-
mizer is not from the already considered search space.
The greedy algorithm helps to reduce the search space
and improves the time efficiency as against the ex-
haustive brute force search in solution space.
The pseudo code in algorithm 2, describes the
greedy algorithm, in which the long-term memory of
GlobalOptimalSolutiontoSLAMProblemwithUnknownInitialEstimates
79
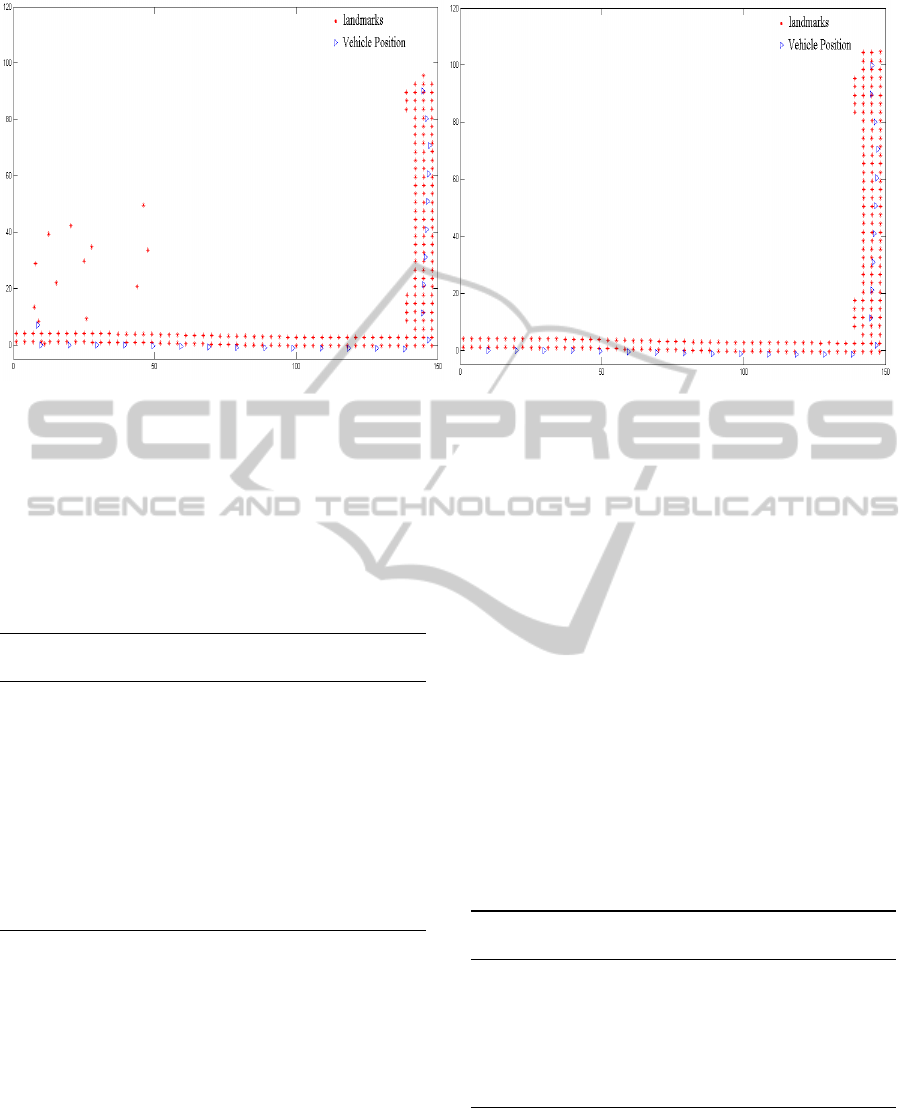
(a) Before joining (b) After joining
Figure 4: Intermediate results of simulation dataset (S. Huang and Frese, 2008) with 50 local maps.
all the solution space is maintained. The selection
of new feasible solution is determined similar to 1D
explained approach on orientation space (as vehicle
and feature positions are linear with respect to orien-
tation). Selection of ε in radians decides the selection
of new hypothesis for initial guess to boot the local
optimizer.
Algorithm 2: GRASP-Algorithm: Randomized greedy al-
gorithm.
while Initial guess not found | Max iter not reached do
x = random(.)
f ound = 1
for i=1:num of elements in LTmemoryX do
Oldx = LTmemoryX[i]
if |(x − Oldx)| < ε then
found = 0
Break → select another x
end if
end for
end while
return x
An appealing characteristic of GRASP approach
is the ease of implementation by setting and tuning
few parameters. The computation time of the ap-
proach does not vary much from iteration to iteration
and increases linearly with the number of iterations
whereas the time increases combinatorially with the
increase of searched spaced parameters.
6 GLOBAL OPTIMAL SOLUTION
TO MAP-JOINING
Most of the map joining approaches start with linear
approximation of map states and do optimization as
a post processing step to estimate the local solu-
tion (S. Huang and Frese, 2008; S. Huang and Dis-
sanayake, 2008; K. Ni, 2007). Our approach is not
dependent upon the initial guess and bound to search
the optimal results by modified GRASP approach. We
initialized each map randomly (unknown feature and
vehicle pose) and solve the map joining problem as
illustrated in pseudo code algorithm 3. The data asso-
ciation is assumed to be known. Two maps are consid-
ered at each time and provided to GRASP algorithm,
which returns the optimal solution for those two sets
of maps observation. The sequential joining is not
necessary and parallel algorithm can be employed for
faster computation, if the running time is bottleneck
in a large scale environment. The input to algorithm 1
will be set of observations (relative feature and odom-
etry information of local maps l) and global map state
vector X,M to obtain x
∗
.
Algorithm 3: MAP Joining Optimal: GRASP variant for
Map Joining.
x* = first local map
while Fuse local map k+1(l) into x* do
Data Association assumed to be known
Initialize random pose/landmark for l into x*
x*= GRASP-Algorithm (x*, Local Map l)
end while
return x*
7 RESULTS AND DISCUSSION
The performance of the proposed algorithm is tested
on simulated (S. Huang and Frese, 2008) as well on
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
80
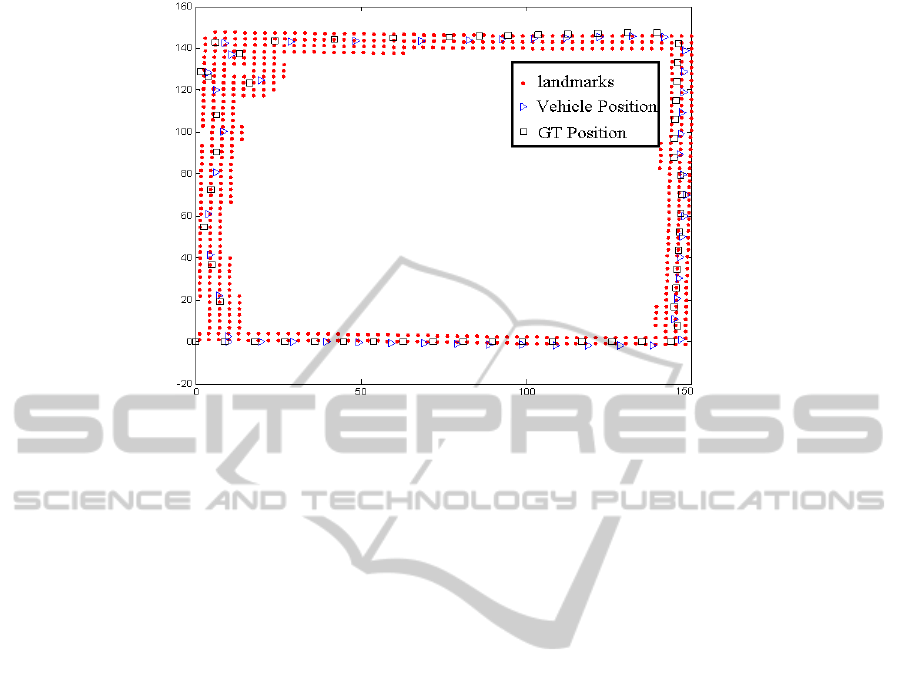
Figure 5: Ground truth and estimated vehicle/landmark positions for simulation dataset (S. Huang and Frese, 2008) with 50
local maps.
real dataset (J. Kurlbaum, 2010), which are both avail-
able publicly. The 150 × 150m
2
simulation environ-
ment (S. Huang and Frese, 2008) containing 2500 fea-
tures uniformly space in rows and columns is tested
first. The robot started from the left bottom corner
of the square and followed a big loop. A sensor
with a field of view of 180 degrees and a range of
6 meters was simulated to generate relative range and
bearing measurements between the robot and the fea-
tures. There were 50 local maps in total with 612
observed features and 1374 odometry/feature mea-
surements were made from the robot poses. Fig.
4(a) shows the intermediate results of 25
th
local map
where new local map with random initial guesses
of landmark position and pose. The GRASP based
smoothing is performed and optimal results obtained
is shown in Fig. 4(b). Final results with ground truth
result is shown in Fig. 5, showing estimated position
against the interpolated ground truth positions.
The GRASP based approach with unknown initial
guess is tested on DLR dataset (J. Kurlbaum, 2010)
and compared with the state of the art map-joining
approach (S. Huang and Frese, 2008). DLR dataset is
acquired with a camera attached on a wheeled robot
and odometry. The robot moved around a building
detecting scattered artificial white/black landmarks,
placed on the ground. Odometry measurements and
relative position of the observed landmarks are being
provided. 200 local maps with 540 observed features
and 1680 odometry/feature observations is considered
with known data association. Fig. 6 (a) shows the
random initial guess for vehicle pose and feature po-
sitions in global frame of reference, to be processed
by GRASP approach. Fig. 6 (b and c) shows a visual
comparison of proposed approach with (S. Huang and
Frese, 2008) whereas (S. Huang and Frese, 2008) ap-
proach is booted with linear initialization and our pro-
posed approach is not dependent upon known initial
guess. Gaussian noise is introduced into the odome-
try observations (which makes inconsistency between
odometry and feature observations) to gauge the per-
formance of proposed approach, hence we are able to
get a global solution each time, which is optimum in
Maximum likelihood sense whereas local optimiza-
tion based approaches results in local solution similar
to Fig. 1. The performance of the experimental results
validates the proposed idea and makes the SLAM
problem solvable by global optimization based ap-
proach without initial guess.
8 CONCLUSIONS AND FUTURE
WORKS
A practical approach for finding the globally optimal
solution to SLAM is presented. Local optimization
based strategies which are mostly adopted for SLAM
problem are highly susceptible to local minima prob-
lem due to non-convex structure of the problem. By
exploiting the theoretical limit on the number of lo-
cal minima, we proposed a framework to estimate
a global optima. The proposed approach is not re-
liant on good initial guess which is the primary condi-
tion of local optimization based approaches for global
convergence. Experimental results are provided on
different datasets available online to validate the ro-
bustness of approach.
GlobalOptimalSolutiontoSLAMProblemwithUnknownInitialEstimates
81
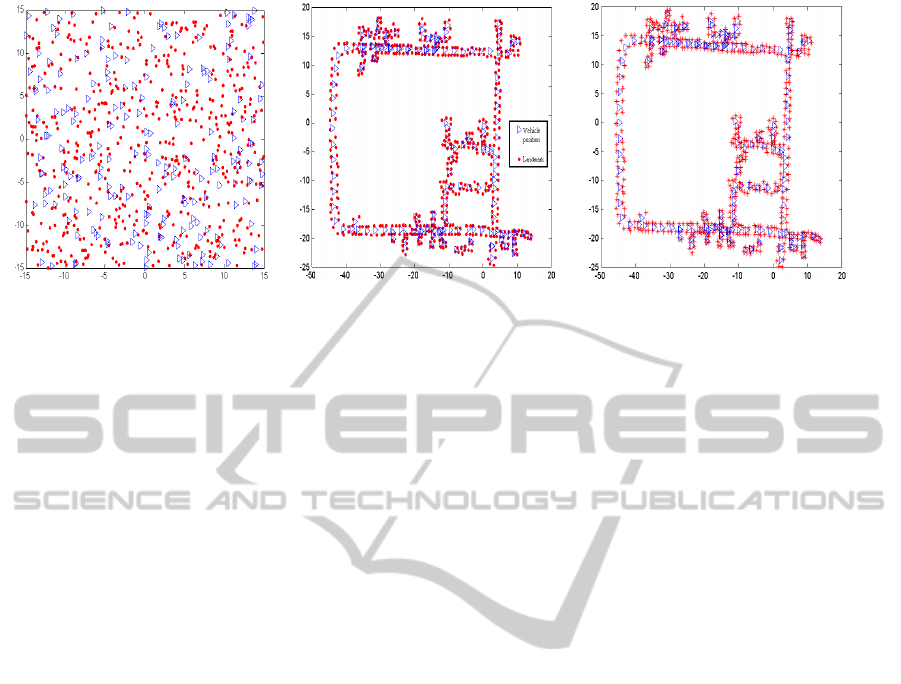
(a) Random initial guess for local maps (b) GRASP based vehicle/landmark position
estimates
(c) I-SLSJF with EIF based initialization
(S. Huang and Frese, 2008)
Figure 6: DLR dataset results using GRASP with 200 local maps, showing global convergence (b) with random initial guesses
(a).
Future work will provide the time/memory com-
parison of the proposed approach and possible exten-
sion to 6DOF SLAM problem.
ACKNOWLEDGEMENTS
This work is supported by the ARC DP Project
(DP0987829) funded by the Australian Research
Council (ARC). We are also thankful to (J. Kurlbaum,
2010) and (S. Huang and Frese, 2008) for open source
implementation and datasets.
REFERENCES
A. Doucet, N. Freitas, K. M. and Russel, S. (2002). Black-
wellized particle filtering for dynamic bayesian net-
works. In International Conference on Uncertainty in
Artificial Intelligence, pp. 17618.
Bailey, T. and Durrant-Whyte, H. (2006). Simultaneous
localization and mapping (slam): part ii. In IEEE
Robotics and Automation Magazine, vol. 13, issue 3,
pp. 108-117.
C. Olsson, F. K. and Oskarsson, M. (2008). Branch and
bound methods for euclidean registration problems. In
IEEE Transactions on Pattern Analysis and Machine
Intelligence.
C.Blum and A.Roli (2003). Metaheuristics in combinatorial
optimization: Overview and conceptual comparison.
In ACM Computing Surveys, vol.35, no. 3.
Dellaert, F. and Kaess, M. (2006). Square root sam: si-
multaneous localization and mapping via square root
information smoothing. In Journal of Robotics Re-
search, vol. 25, no. 12, pp. 1181-1203.
E. Olson, J. L. and Teller, S. (2006). Fast iterative opti-
mization of pose graphs with poor initial estimates. In
IEEE International Conference on Robotics and Au-
tomation (ICRA), pp. 2262-2269.
Freund, R. and Jarr, F. (2001). Solving the sum-of-ratios
problem by an interior-point method. In Journal of
Global Optimization.
Iser, R. and Wahl, F. (2010). Antslam: global map optimiza-
tion using swarm intelligence. In IEEE International
Conference on Robotics and Automation (ICRA), pp.
265-272.
J. Kurlbaum, U. F. (2010). A benchmark data
set for data association. In Technical Re-
port, University of Bremen, Data Available on
http://cres.usc.edu/radishrepository/.
K. Astrom, O. Enqvist, C. O. F. K. and Hartley., R. (2007).
An l∞ approach to structure and motion problems in
1d-vision. In International Conference on Computer
Vision (ICCV).
K. Ni, D. Steedly, F. D. (2007). Tectonic sam: ex-
act, out-of-core, submap-based slam. In IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pp.16781685.
Lu, F. and Milios, E. (1997). Globally consistent range scan
alignment for environment mapping. In Journal of Au-
tonomous Robots, pp.333349.
R. Kummerle, G. Grisetti, H. S. K. K. and Burgard, W.
(2011). g2o: A general framework for graph optimiza-
tion. In IEEE International Conference on Robotics
and Automation (ICRA).
Resende, M. and Ribeiro., C. (2003). Greedy randomized
adaptive search procedures. In Handbook of Meta-
heuristics, pp. 219249.
S. Huang, Z. Wang, G. D. and Frese, U. (2008). Iterated
slsjf: A sparse local submap joining algorithm with
improved consistency. In Australiasan Conference on
Robotics and Automation (ACRA).
S. Huang, H. Wang, U. F. and Dissanayake, G. (2012). On
the number of local minima to the point feature based
slam problem. In IEEE International Conference on
Robotics and Automation (ICRA), pp. 265-272.
S. Huang, Z. W. and Dissanayake, G. (2008). Sparse lo-
cal submap joining filter for building large-scale maps.
In IEEE Transactions on Robotics, vol. 24, no. 5, pp.
1121-1130.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
82

T. Duckett, S. M. and Shapiro, J. (2002). Fast, on-line learn-
ing of globally consistent map. In Journal of Global
Optimization, pp. 287300.
U. Frese, P. L. and Duckett, T. (2005). A multilevel re-
laxation algorithm for simultaneous localization and
mapping. In IEEE Transactions on Robotics, vol. 21,
no. 2, pp. 196-207.
GlobalOptimalSolutiontoSLAMProblemwithUnknownInitialEstimates
83
