Broken Bar Fault Detection based on Set Membership Identiﬁcation for

Three Phase Induction Motors

Mohammed Obaid Mustafa

, George Nikolakopoulos

, Thomas Gustafsson

and Basil M. Saied

Department of Computer Science, Electrical and Space Engineering, Division of Systems and Interaction,

Lule˚a University of Technology, Lule˚a, Sweden

Department of Electrical Engineering, University of Mosul, Mosul, Iraq

Keywords:

Three Phase Induction Motor, Fault Detection, Set Membership Identiﬁcation.

Abstract:

This article presents a fault detection scheme for the case of a broken bar occurrence in a three phase induction

motor. The proposed scheme relies on Set Membership Identiﬁcation (SMI) and novel proposed boundary

violation rules for the identiﬁed motor’s parameters. The model of the three phase induction motor is being

transformed into an equivalent two phase model, described in the q −d space, for both the normal and the

faulty case. By the utilization of the SMI technique, the simpliﬁed equivalent model of the induction motor is

being identiﬁed during the steady state operation (non–fault case), while at the same time safety bounds for the

identiﬁed variables are being provided, based on an a priori deﬁned corrupting additive noise. On the event of

a fault, speciﬁc fault detection conditions are being proposed that can capture the speciﬁc type of a broken bar

fault. The proposed conditions depend on: a) abnormal parameter jumps, and b) rapid changes in the volume

of the bounding uncertainty, which is being formulated either by ellipsoids or orthotopes. Detailed analysis of

the proposed approach as also extended simulation results are being presented that prove the efﬁciency of the

proposed scheme.

NOMENCLATURE

, V

: Stator’s three phase voltages (V)

, V

: Rotor’s three phase voltages (V)

, i

: Rotor’s three phase currents (A)

, i

: Stator’s three phase currents (A)

, r

: Resistance of stator’s and rotor’s wind-

ing (Ohm)

, L

: Stator’s and rotor’s self–induct-

ances (Henry)

, L

: Stator’s and rotor’s self inductance (Henry)

: Mutual inductance (Henry)

: Rotor’s angular speed (rad/sec)

: Rotor’s speed (mechanical) (rad/sec)

: Supply angular frequency (rad/sec)

P : No. of poles pairs

J : Moment of inertia (Kg·m

)

: Load torque (Nm)

: Electromagnetic torque (Nm)

q : Quadrature axis frame

d : Direct axis frame

s : Stator quantities

r : Stator quantities

, Ψ

: Stator’s and Rotor’s ﬂuxes (Weber)

θ : Angular position in the frame of motor (Deg)

: Angle between rotor’s phase axis and stator’s

phase axis

β : Angle between rotor’s phase axis and stator’s

phase axis

: Numbers of machine rotor bars

1 INTRODUCTION

The three phase induction motor is one of the most

important types of motors that are commonly being

found in many industrial applications, mainly due to

their efﬁciency and reliability (Chen and Zivanovic,

2009), due to the fact that these motors are operating

in difﬁcult working environments with many factors

that degrade their performance such as: dust, tem-

perature level, humidity, continuous operation, and

heavy loads, internal faults frequently occur.

The most common faults that could be appeared in

the rotor and the stator of an induction motor are: a)

short circuit stator winding (Nandi and Toliyat, 2005),

b) broken rotor bars (Santos and Lubiny, 2010), c)

bearing failures, and d) dynamic or static air gab ir-

224

Obaid Mustafa M., Nikolakopoulos G., Gustafsson T. and M. Saied B..

Broken Bar Fault Detection based on Set Membership Identiﬁcation for Three Phase Induction Motors.

DOI: 10.5220/0004040202240231

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 224-231

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

regularities (Nandi and Toliyat, 2005). From all these

types of faults, the broken bar faults comprise around

(5-10)% of all the reported motor faults, while it is

necessary to detect this type of fault, as soon as possi-

ble as these type of faults can add serious motor dam-

age if not detected on time .

In general for detecting the mechanical or elec-

trical faults in a three phase induction motor mul-

tiple methods have been proposed, which can be

categorized in direct and indirect methods. Direct

methods base their operation on spectral analysis of

stator currents, stator voltages, and electromagnetic

torque (Bachi et al., 2006), with the focus to be on

detecting spectrum lines at certain frequencies using

classical methods like Fouriers analysis and are quite

simple to be implemented. A signiﬁcant drawback

of these methods is the fact that these are best suited

for ﬁxed speed applications, while in industrial appli-

cations under varying speed and with a direct power

supply, these methods are not well adapted due to the

fact that the involved electrical signals are not station-

ary. Indirect methods base their operation on identiﬁ-

cation or prediction techniques and multiple identiﬁ-

cation schemes for fault detection and fault diagnosis

have been appeared in the literature.

In parallel to these indirect fault detec-

tion schemes, Set Membership Identiﬁcation

(SMI) (Deller, 1989; Deller et al., 1993) has received

a growing attention in the past years as a quite

important technique for system identiﬁcation with

uncertainty bounds. The main novelty of this article

stems from the adaptation of the SMI approach to

the problem of fault detection and more speciﬁcally

to the problem of detecting broken rotor bar fault for

an induction motor. To the author’s best knowledge

this is the ﬁrst time that such an approach is being

reported in the scientiﬁc literature. The extension

of this scheme to other types of faults can support

a general fault detection framework, where fault

diagnosis could be also performed in parallel with

the fault detection scheme. Based on the proposed

approach, the three phase model of the induction

motor is being transformed to an equivalent two

phase model for the healthy and the faulty case,

and the safety intervals for the online SMI for the

identiﬁed parameters, are establishing a robust fault

detection scheme that could be directly transferred to

real–life implementations.

The rest of the article is being structured as it fol-

lows. In Section 2 the model derivation and simpliﬁ-

cation, for the healthy and the faulty cases are being

derived. In Section 3 the SMI scheme is being pre-

sented, followed by the proposed fault detection con-

ditioning framework in Section 4. Section 5 contains

multiple simulation results that prove the efﬁcacy of

the proposed methodology, while the conclusions are

drawn in the last Section 6.

2 INDUCTION MOTOR

MODELING

2.1 Healthy Case

In general an induction motor can be modeled as

a three phase model or as an equivalent quadrature

phase model, while the voltage balance equations for

the case of three phases can be formulated as (Vas,

1992):

V = p ψ + R i

where

V = [V

]

ψ = [ψ

]

i = [i

]

R = diag





and r

= r

and r

= r

in the balance

case of motor, the operator p is equal to d/dt and the

equations of three phase input voltages are:

= V

sin(ω

= V

sin(ω

t −2π/3) (1)

= V

sin(ω

t −4π/3)

and the relation between the phase linkages and the

phase currents is provided by:

ψ = L i (2)

L pi = V−R i

In this formulation the values of the inductance

matrix L depend on the rotor’s electrical angle and

the type of the utilized model (Chen and Zivanovic,

2009). For simplifying the three phase model,

the equivalent two phase model will be extracted

that has been converted to the q − d coordination

frame (Sandhu and Pahwa, 2009). For predicting the

mechanical and electrical behavior of the original ma-

chine correctly, the original abc variables F

abc

should

be transformed into the corresponding d −q variables

qdo

and this is being carried out through Park’s trans-

form as it follows (Lee et al., 1985):

dqo

= T

qdo

·F

abc

(3)

dqo

= T

qdo

·V

abc

(4)

dqo

= T

qdo

·i

abc

(5)

BrokenBarFaultDetectionbasedonSetMembershipIdentificationforThreePhaseInductionMotors

225

where

dqo





cosθ cosθ

cosθ

sinθ sinθ

sinθ

1/2 1/2 1/2





(6)

and

dqo

= [v

]

(7)

dqo

= [i

]

(8)

with θ

= θ − 2π/3, θ

= θ −4π/3. In the case

that the saturation and the fraction effects are being

neglected, the balance voltage equation of the three

phase induction motor in q −d model are provided

by:

= V

−R

(9)

and the pi

can be calculated as:

= −L

−1

+ L

−1

(10)

where

= [v

]

(11)

= [i

]

(12)







0 L







(13)

and







0 0 0

0 r

0 0

0 −ω

/ω

rr −ω

/ω

0 ω

/ω







(14)

After these formulations, equation (10) can be re–

written in a state space form as:













= A













+ B













(15)

where:

A = −R

−1

(16)

B = L

−1

(17)

and with the A and B matrices deﬁned as:

A =







−L

0 L

0 −L

0 L

0 −L

0 L

−w

δ −L







(18)

B =







0 −L

0 L

0 −L

−L

0 Ł

0 −L

0 L







(19)

while δ is given as:

δ = L

−Lm

(20)

Finally, the resulting equations for the torque and the

mechanical angular speed for the three phase induc-

tion motor are:

P L

−i

] (21)

dω

−T

]dt (22)

2.2 Broken Bar Model of Three Phase

Induction Motor

The focus of this research effort is on the identiﬁca-

tion of broken bar faults in the rotor of a three phase

induction motor. The reasons of broken bar faults are

thermal, magnetic, residual, dynamic, and mechan-

ical stresses (Nandi and Toliyat, 2005). The event

of a broken rotor bar causes asymmetry of the resis-

tance and inductance in rotor phases, which results

in asymmetry of the rotating electromagnetic ﬁeld in

the air gap between stator and rotor. Consequently,

this will induce frequency harmonics in the stator cur-

rent. The impact of broken rotor bars can be mod-

eled by unbalancing the rotor resistance, while the

inductance changes are being neglected due to their

insigniﬁcance inﬂuence compared to the resistance

changes (Bellini et al., 2001; Chen and Zivanovic,

2009), and the stator resistances and inductances stay

unchanged (Chen and Zivanovic, 2009). For simplic-

ity, for a squirrel-cage rotor,the end–ring contribution

is being also neglected.

In the case of such a fault, the modiﬁed (faulty)

versions of matrices A

∗

should be utilized. The modi-

ﬁed rotor resistance matrix in the abc reference frame

can be derived as (Chen and Zivanovic, 2009):





+ ∆r

0 0

0 r

+ ∆r

0 0 r

+ ∆r





(23)

where ∆r

, ∆r

and ∆r

represent rotor resistance

changes in phase a, b and c, respectivelydueto broken

bar faults. The resistance changes are being derived

based on the assumption that the broken bars are con-

tiguous, neither the end ring resistance nor the magne-

tizing current is taken into account. For the case of n

broken rotor bars, the increment ∆r

ra,b,c

in each phase

is being obtained as (Chen and Zivanovic, 2009; Ku-

mar et al., 2011).

∆r

ra,b,c

= r

−3n

(24)

To simulate broken rotor bar fault, the rotor resistance

matrix needs to be replaced by the modiﬁed rotor re-

sistance matrix r

and transformed to q−d reference

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

226

frame, by utilizing the stationary reference frame. For

the cased examined, the rotor resistance changes in

the q −d reference frame as (Chen and Zivanovic,

2009).

∆r

qd0

r f





r11

r12

r13

r21

r22

r23

r31

r32

r33





(25)

where

r11

(∆r

+ ∆r

) +

(2∆r

−∆r

)cos(2θ

)

√

(∆r

−∆r

)sin(2θ

)

r12

= −

(2∆r

−∆r

))sin(2θ

) +

√

(∆r

−∆r

)cos(2θ

)

r13

(2∆r

−∆r

))cos(θ

) −

√

(∆r

−∆r

)sin(2θ

)

r22

(∆r

+ ∆r

) −

(2∆r

−∆r

)cos(2θ

)

√

(∆r

−∆r

)sin(2θ

)

r23

= −

(∆r

+ ∆r

)sin(θ

) −

√

(2∆r

−∆r

)cos(2θ

)

r33

(∆r

+ ∆r

)

r21

= r

r12

r31

r13

r32

r23

and the matrix R

will be also affected, due to the

broken bar fault as:

∗







0 0 0

0 r

0 0

0 −ω

/ω

−ω

/ω

0 ω

/ω







(26)

with:

= r

+ r

r11

= r

+ r

r22

(27)

Therefore the matrices A

∗

, B

∗

in the faulty case will

become:

∗

= −R

∗

−1

(28)

with

∗







−L

0 L

0 −L

0 L

0 −L

0 L

−w

δ −L







∗

= B (29)

In the sequel the q−d model of the induction motor

is being transformed to a MIMO ARMA system that

can be provided by:







(t)













(t)













(t)













(t)







(30)

where θ

(t) is the parameter vector sets and the

subindex j represents the current set that can be se-

lected as one from: [qs, ds, qr, dr]. Moreover θ

(t)

contains the corresponding coefﬁcients of the selected

ARMA model and can be deﬁned in the general case

as:

(t) = [F

j,1

(t) ... F

n,1

(t), T

j,1

(t), ..., T

m,1

(t)]

(31)

Where n and m are the orders of the numerator and de-

nominator for each considered transfer function respec-

tively. The regression vector Φ

(t) is being formulated

as:

(t) = [−y

(t −1), ... ,−y

(t −n), ... , u

(t + m−n−1), ... , u

(t −n)]

In (30) corrupting noise effecting the measurements

is also taken under consideration, while it is assumed

that this noise sequence is bounded by γ

∈ ℜ

as:

||e

(t)||

≤ 1, ∀t (32)

Finally the parameters in (31) have a direct relation

with the motor’s parameters in both the healthy and

the faulty case. For example, for the case of j = qs

for the faulty case, these parameters can be deﬁned

as:

qs,1

, T

qs,2

= −b

+ a

)

qs,3

= b

+ a

−a

+ a

)

qs,4

= b

+ a

−a

qs,1

= (2a

−a

+ a

)

qs,2

= a

+ a

+ 2a

−a

+2a

−a

+ a

qs,3

= a

−a

) + 2a

−a

+ a

)

+2a

−a

+ a

)

qs,4

= a

+ a

−a

+ a

) + a

)

with:

= −(L

)/δ a

= −(L

)/δ b

= L

/δ

= (L

)/δ a

= ω

= −L

/δ

= (L

)/δ a

= (L

)/δ a

= −(L

)/δ

3 SET MEMBERSHIP FAULT

IDENTIFICATION

Set membership identiﬁcation (SMI) refers to a class

BrokenBarFaultDetectionbasedonSetMembershipIdentificationforThreePhaseInductionMotors

227

of techniques for estimating parameters of linear sys-

tems or signal models under a priori information that

constrains the solutions to certain sets. The objective

of the SMI technique is the determination of the fea-

sible parameter set that contains the nominal parame-

ter vector and is consistent with a linearly parameter-

izable model, the measurement data and the a priori

known bounded noise–error. Due to the complexity

in computing the feasible parameter set, the major-

ity of the SMI methods aims at the determination of

a more conveniently computable parametric set that

outer bounds the feasible parameter set (Ljung, 1987;

Deller, 1989).

The SMI technique is based on the Weighted Re-

cursive Least Squares (WRLS) with a forgetting fac-

tor for identifying the

motor’s parameters and

can be formulated by the following double recur-

sions (Guastafsson, 2001) in the sample instance t and

for the MIMO case j as:

(t) =

(t −1) + K

(t)(y

(t) −Φ

(t)θ

(t −1))

(t) = P

(t −1)Φ

(t)(λ+ Φ

(t)P

(t −1)φ

(t))

−1

(t) = (I −K

(t) Φ

(t))P

(t −1)/λ

(t) = y

(t) −Φ

(t)θ

(t −1)

(t) = Φ

(t)P

(t −1)Φ(t)

In the SMI approach the initial bounds γ for the cor-

rupting noise ε

(t) are being re–calculated in every it-

eration. This optimization in the uncertainty descrip-

tion is evolving with the time, as the better the knowl-

edge of the parameters is, the smaller these bounds

are. To calculate the optimal value of λ

∗

(t) for achiev-

ing convergence, the maximum positive root of the

following equation should be extracted in each itera-

tion:

(λ

) = α

2, j

+ α

1, j

+ α

0, j

2, j

= (ℓ + n−1)G

1, j

= (2ℓ + 2n−1+ γ

) −ξ

0, j

= (ℓ + n) ∗(1−γ

) −ξ

(t) = ξ

(t −1) +

−

1−λ

with ℓ = m + 1. For founding the upper and lower

boundary for the identiﬁed parameters, the uncer-

tainty bound σ

(t), should be computed in every it-

eration. For delivering these bounds, the smallest or-

thotope that bounds the ellipsoidal uncertainty of the

parameter and it is oriented parallel to the parameter

coordinate axes and centered on the centroid of the

ellipsoid is being calculated as:

(t) =

diag(P

(t)) (33)

while the corresponding equation for the ellipsoids

Ω

(t) and the orthotopes Ω

(t) can be calculated

as (Deller, 1989):

Ω

(t) = {θ

: (θ

(t) −

(t))

(t)

)(θ

(t) −

(t)) ≤ 1, j = 1, ...., n+ m}

Ω

(t) = {θ

: (

|σ

(t)|

)(θ

(t) −

(t)) ≤ 1, j = 1, ...., n+ m}

with the orthotope’s vertices V

n+m+1

j, o

(k), o =

0,.. .,2

n+m+1

−1 are related to the σ

parameters as:

j, o

(k) = θ

(t) + [α

∗

j, n+m+1

(t), . ..,α

j, 1

(t)]

where α

∗

j,(·)

(

+ when a

j, (·)

= 1

− when a

j, (·)

= 0

, and the co-

variance matrix is denoted as C

(t) = P

(t)

−1

. The

matrix W(t) =

(t)

will represent how far the ellip-

soid extends in each direction from the center of the

ellipsoid

(t), while the volume ratio of the j ellip-

soid is being calculated by: B

(t) = det

−1

(W(t)).

4 FAULT DETECTION

CONDITIONING

In the case of a broken bar fault occurrence, the values

of the identiﬁed parameters will be characterized by a

jump and a constant drift from the converged nominal

values of the healthy motor. This jump has a direct

effect on the updated parameter’s bounds, as after the

event of the fault the following calculated uncertainty

bounds will exceed the previous calculated bounds in

the healthy case, while this situation is a direct indi-

cation of a fault occurrence. Based on the proposed

SMI scheme, the following rules for the fault occur-

rence identiﬁcation will be established as it is being

depicted in Figure 1. In the presented approach it

has been assumed that the SMI scheme is providing

smooth value updates for the identiﬁed parameters.

If a t

time window is being deﬁned, then after

the convergence of the parameters, small changes

in the identiﬁed values should be allowed, while a

signiﬁcant change might indicate the occurrence of a

fault. For the ad–hoc deﬁned bound B

the ﬁrst fault

detection condition is being formulated as:

[Condition 1] |θ

(k) −

(k−t

: k)| ≥ B

where θ

(k) denotes the converged identiﬁed

parameter and the notation · represents a moving

average time window of length t

. Two additional

rules can be deﬁned, that are related with the volumes

of the bounding ellipsoids Ω

or orthotopes Ω

. The

aim is to track the corresponding volumes of the

bounding ellipsoid/orthotope and allow only small

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

228

Set Membership

Identification

Three Phase

Induction Motor

θ -θ (k-t : k) >B

Ω -Ω (k-t :k) >B

Fault Detection

Conditioning

Fault

Occurrence

Figure 1: Faults detection scheme.

changes, as in the opposite case, this should generate

a fault. By deﬁning two ad–hoc boundaries as B

and B

and two additional time windows t

, t

, the

following additional fault detection conditions can be

formulated:

[Condition 2] |Ω

e,o

(k) −Ω

(k−t

) : k| ≥ B

[Condition 3] |Ω

p,o

(k) −Ω

(k−t

: k)| ≥ B

Where Ω

e,o

,Ω

p,o

are the converged values and

conditions (2) and (3) are complimentary and

depending on the processing capabilities and the

accuracy that we would like to achieve. In general,

condition (2) is more accurate that condition (3), as

the orthotope is bounding the uncertainty described

by the ellipsoid, but this approach has the drawback

that it is more computational demanding.

5 SIMULATION RESULTS

The suggested scheme for fault detection is being

evaluated on a model of three phase induction motor

having the parameters depicted in Table 1.

Table 1: Induction Motor Parameters.

Pole Numbers 4 r

0.0616 per unit

Input Voltage 240V r

0.0753 per unit

Frequency 50Hz J 0.00155 Kg.m

0.019 per unit L

0.019 per unit

0.01833 per unit N

The ﬁrst simulation results will focus in present-

ing the effect of one broken bar fault occurrence on

the rotor’s current, torque and angular speed, as it is

1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2

x 10

−3

−2

−1

(Per unit)

1.6 1.61 1.62 1.63 1.64 1.65 1.66 1.67 1.68 1.69 1.7

x 10

1.1

1.105

1.11

1.115

1.12

1.125

Time (Sec)

(Per unit)

Normal case

Faulty case

Figure 2: The rotor’s currents in the normal and faulty case.

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

x 10

−0.5

0.5

1.5

2.5

Torque (Per Unit)

1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9 1.95 2

x 10

0.98

1.02

1.04

Time (Sec)

Torque (Per Unit)

Faulty case

Normal case

Faulty case

Normal case

Figure 3: The torque of the motor in the normal and faulty

case.

1.5 1.55 1.6 1.65 1.7 1.75

x 10

0.903

0.904

0.905

0.906

0.907

0.908

0.909

Time (Sec)

Wr / Ws

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

x 10

−0.2

0.2

0.4

0.6

0.8

1.2

Wr / Ws

Faulty case

Normal case

Faulty case

Normal case

Figure 4: The rotor angular speed of the motor in the normal

and faulty case.

being presented in Figures (2-4) respectively. For the

rotor’s current, same results have been also obtained

as in Figure (2).

From the obtained results, it can be observed that

the small change in the values of the currents can

be distinguished, where the rotor’s current I

in the

faulty case will be increased from the corresponding

value in the healthy case. In Figures (3 and 4), it is

also depicted that the fault is affecting the steady state

values of the rotor’s torque and speed respectively. In

the case of the motor’s torque oscillations are taking

place, while the amplitude of these oscillations is be-

ing increased with respect to the number of the faulty

broken bars. In the second case, the speed is also been

decreased, while oscillations are also evident.

In the sequel, results from applying the proposed

SMI scheme for broken bar fault detection are go-

ing to be presented. Figures (5), and (6) present the

convergence of the SMI identiﬁcation (with the un-

certainty bounds) of the motor’s parameters in the

BrokenBarFaultDetectionbasedonSetMembershipIdentificationforThreePhaseInductionMotors

229

1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

x 10

−4

−2

qs,1

1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

x 10

−4

−2

qs,2

1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

x 10

−0.5

0.5

qs,3

1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

x 10

−0.1

0.1

Sample Index

qs,4

Figure 5: SMI based identiﬁed parameters for F

and cor-

responding uncertainty bounds.

0.5 1 1.5 2 2.5 3

x 10

8.5

9.5

qs,1

1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

x 10

−20

qs,2

1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

x 10

−20

qs,3

1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

x 10

−10

Sample Index

qs,4

Figure 6: SMI based identiﬁed parameters for T

and cor-

responding uncertainty bounds.

8.5 8.6 8.7 8.8 8.9 9 9.1 9.2

8.4

8.6

8.8

qs,1

qs,2

0 1 2 3 4 5 6 7 8 9 10

x 10

−50

Sample index

Ellipsoid volume ratio

−100

100

−50

qs,3

@ 500 Sample

@ 2500 Sample

@ 99000 Sample

Figure 7: Orthotope and ellipsoid change with sample in-

dex.

healthy case, only for the case of having as input V

and output i

, while similar results have been ob-

tained for the rest of the motor’s parameters, but due

to space limitations, those graphs have been omitted.

0 1 2 3 4 5 6 7 8

x 10

8.1

8.2

8.3

8.4

8.5

8.6

8.7

8.8

8.9

Sample index

qs,1

with bounds in normal and faulty case

Moving window

Bounds in faulty case

Bounds in normal case

qs,1

Fault ocurrence

Figure 8: Convergence of the T

qs,1

parameter and corre-

sponding bounds before and after the occurrence of the

fault.

As it can be observed from these ﬁgures the uncer-

tainty bounds are starting from a large value and in

the sequence, as the identiﬁcation procedure is evolv-

ing and the identiﬁed parameters are close to the nom-

inal values, those bounds are being decreased, until it

reach their steady state value. Finally, in Figure (7)

the convergence of the ellipsoid volume and the con-

vergence of the orthotope’s volume is being presented

and the corresponding bound sets of uncertainty are

being presented at different time indexes, where the

evolution of the volume has been highlighted with re-

spect to the sample index.

In Figure 8, the case of a fault occurred at 20000

samples (Sampling time T

= 0.01) is being presented.

Due to this fault a jump in the identiﬁed parameters

is taking place that affects the presented conditions

for fault detection. More speciﬁcally, the uncertainty

intervals are changing (due to the drift in the identi-

ﬁed model) and this leads in a bounds violation event,

which indicates the existence of the broken rotor fault.

Similar graphs can also be extracted for all the identi-

ﬁed parameters of the motor and without loosing gen-

erality, in Figure 8, only the results for T

qs,1

are being

presented.

The effectiveness of the identiﬁcation scheme can

also be examined by inspecting the volume of the

bounding ellipsoid. As it is being displayed in Fig-

ure (7) the ellipsoid volume will be minimized as the

identiﬁed model matches the real one. In the even

of a fault, the identiﬁed values are being drifted to

small values (resulting from the faulty model repre-

sentation) and thus is why the bounds are being kept

on monotonically being decreased. In the case of a

rotor’s broken bar, the operation of the motor is still

unaffected, and the result due to the fault is a small

parametric drift and this is why a the simple inspec-

tion of the identiﬁed parameters in not the only factor

that should be monitored for fault identiﬁcation, but

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

230

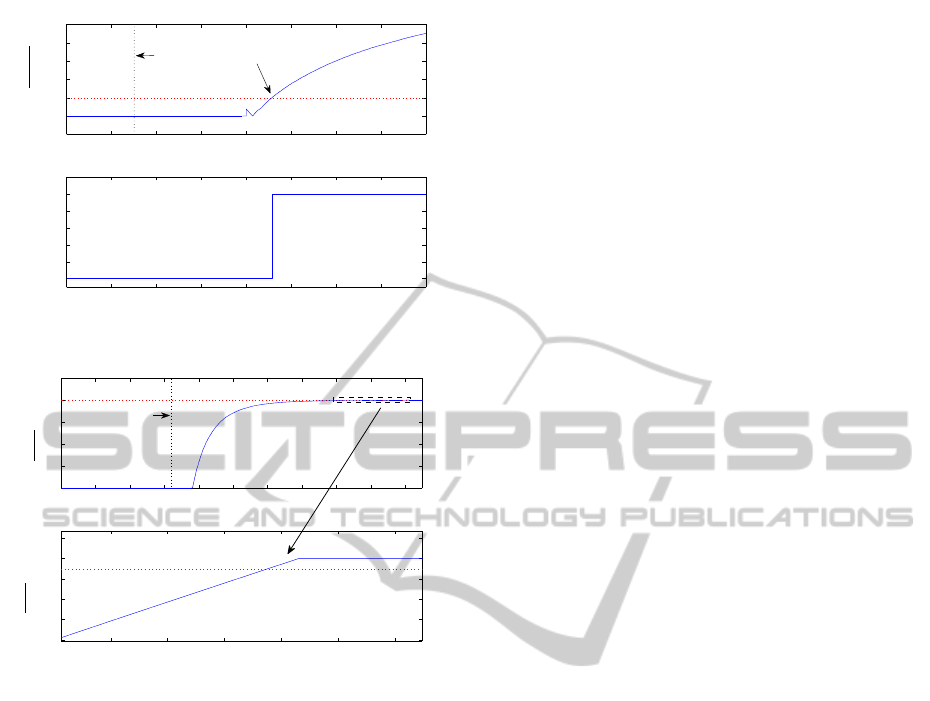
0 0.5 1 1.5 2 2.5 3 3.5 4

x 10

−0.01

0.01

0.02

0.03

0.04

0.05

Sample Index

(k) −

(k − t

: k)|

0 0.5 1 1.5 2 2.5 3 3.5 4

x 10

0.2

0.4

0.6

0.8

Sample Index

Fault detection

Bound violation

convergance

time

=0.01

Figure 9: Fault detection after 1

condition monitoring.

2.002 2.003 2.004 2.005 2.006 2.007

x 10

7.992

7.994

7.996

7.998

8.002

x 10

−11

Sample Index

|(Ω(k − t

) − Ω(k))|

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

x 10

0.2

0.4

0.6

0.8

x 10

−10

Sample Index

|(Ω(k − t

) − Ω(k))|

= 0.8e − 10

Convergance time

Figure 10: Fault detection after 2

condition monitor-

ing/condition2.

is should be combined with the second or third condi-

tion for the ellipsoid or the orthotope’s volume. In the

examined case, the occurrence of the fault has caused

a jump on the ellipsoid’s volume convergence, which

was bigger than the a priori deﬁned bound and thus

the algorithm is able to trigger the even of the fault.

The time evolutions of the fault detection con-

ditions are being presented in Figures (9) and (10)

where the convergence time for the identiﬁed param-

eters is also being displayed, along with the bound

violation for the conditions (1) and (2).

6 CONCLUSIONS

In this article a fault detection scheme for broken ro-

tor bar fault detection has been presented in the case

of a three phase induction motor. The three phase in-

duction motor has been modeled in the equivalent two

phase motor (q−d) space, while the modeling of the

faulty case has been also formulated. The motor has

been identiﬁed by the utilization of the SMI algorithm

that has the merit of identifying both the parameters of

the motor as also providing uncertainty safety bounds

by calculating ellipsoids/orthotopes, which bounds

the systems parameter vector. The obtained results

present the efﬁciency of the proposed conditions to

capture the event of the fault.

REFERENCES

Bachi, S., Tnani, S., Trigeassou, J., and Champenois,

G. (2006). Diagnosis by parameter estimation of

stator and rotor faults occurring in induction ma-

chines. IEEE Transactions on Industrial Electronics,

53(3):963–973.

Bellini, A., Filippetti, F., Franceschini, G., Tassoni, C., and

Kliman, G. (2001). Quantitative evaluation of induc-

tion motor broken bars by means of electrical signa-

ture analysis. IEEE Transactions on Industry Appli-

cation, 37(5):1248–1255.

Chen, S. and Zivanovic, R. (2009). Modelling and sim-

ulation of stator and rotor fault conditions in induc-

tion machines for testing fault diagnostic techniques.

European Transactions On Electrical Power, 20:611

–629.

Deller, J., Nayeri, M., and Odeh, S. (1993). Least–Square

Identiﬁcation with Error Bounds for Real–Time Sig-

nal Processing and Control. Proceedings of the IEEE,

81(6):815–849.

Deller, J. R. (1989). Set membership identiﬁcation in digital

signal processing. IEEE ASSP Magazine, 6(4):4–20.

Guastafsson, F. (Sep.2001). Adaptive Filtering and Change

Detection.

Kumar, S., Prakash, J., and Kumar, S. S. (2011). Detection

of broken rotor bars in induction motor using deriva-

tive free kalman ﬁlters. International Conference on

Process Automation, Control and Computing (PACC),

2011, pages 1 – 7.

Lee, R., Pillay, P., and Harley, R. (1985). Dq reference

frames for the simulation of induction motors. Elec-

tric Power Systems Research, 8:15 –26.

Ljung, L. (1987). System Identiﬁcation Theory For The

User. Prentice–Hall, Englewood Cliffs, NJ.

Nandi, S. and Toliyat, H. (2005). Condition monitoring and

fault diagnosis of electrical machines-a review. IEEE

Transactions on Energy Conversion, 20(4):719–729.

Sandhu, K. and Pahwa, V. (2009). Sumilation study of three

phase induction motor with variation in moment of in-

ertia. ARPN Journal of Enginering and Apllied Sci-

ences, 4(5):72–77.

Santos, P. and Lubiny, T. (2010). A simpliﬁed induction

machine model to study rotor broken bar effects and

for detection. European Transactions On Electrical

Power, 20:611.

Vas, P. (1992). Electrical Machines and Drives.

BrokenBarFaultDetectionbasedonSetMembershipIdentificationforThreePhaseInductionMotors

231