
Using Forward-backward Contractors to Identify Parasitic Parameters
of Electrical Circuits Working in High Frequency
Nacim Meslem, C
´
ecile Labarre and St
´
ephane Lecoeuche
Univ Lille Nord de France, EM Douai, IA, Douai 59500, France
Keywords:
Electrical Circuit, Electrical Parasitic Parameters, Input Impedance, Interval Analysis, Forward-backward
Contractor, Set-membership Estimation.
Abstract:
Parasitic parameters in electrical networks are usually sources of intolerant electromagnetic interference in
their near environment. In order to understand better the undesirable phenomenon, the values of these unknown
parameters must be estimated with a good accuracy. This work shows how interval analysis can help designing
set-membership algorithm that is able to solve with numerical guarantee the kind of issue. A simple example,
namely second order filter, is studied and our method shows promising performances for dealing with complex
circuits.
1 INTRODUCTION
Electromagnetic Interference (EMI) filters are widely
used in power electronics. In order to efficiently pre-
dict their performance, EMI filters should be charac-
terized and specially their parasitic parameters, which
assume an important role in high frequency. The ef-
fects on filter performance of the parasitic capacitance
in an inductor and the parasitic inductance in a capac-
itor are well-known (Chen et al., 2008). These ef-
fects can be measured with an impedance analyzer
(Labarre and Costa, 2011) or a network analyzer
(Wang et al., 2005) and correctly modeled. Even-
tually, these parasitic effects can be modeled using
3D simulators. The parasitic effects related to the
layout and the packaging are more difficult to grasp
and then to model. In the literature, few works at-
tempted to solve this issue. For example, in (Kotny
et al., 2009) the authors present a fitting approach
using impedance measurements. However, this ap-
proach is based on approximations and does not take
into account the noises that constantly affect the mea-
sured values. Moreover, the user of this fitting method
must manually analyze the experimental data in or-
der to be able to apply the proposed approximations.
Motivated by these problems, we present in this work
a set-membership estimation algorithm that can deal
with corrupted data (Jaulin et al., 2001). In fact, our
set-membership estimation method assumes that the
corrupted data are unknown but belong to a set with
known bounds. Then, it discards in a rigorous way
portions of the search space where the parasitic pa-
rameters are inconsistent with the impedance mod-
els, the experimental data and the priori known er-
ror bounds (Jaulin et al., 2001). That means, the set-
membership method computes an outer approxima-
tion of the feasible parameters set. Additionally, this
method makes the uncertainty in the estimated param-
eters directly available from the shape and the size of
the outer approximation of the solution set. Indeed,
the projections of the outer approximation onto the
parameters axes constitute uncertainty intervals for
the identified parameters. Moreover, compared to the
classical identification methods (Buiatti et al., 2007)
based on stochastic assumptions, the set-membership
approach requires much less of experimental data and
takes into account the deterministic modeling error.
In fact, the classical identification methods are rel-
evant only when an explicit characterization of the
measurement noise is available. It is important to
note that, for our parameters estimation problem, de-
terministic modeling and measurement error cannot
adequately be described by random variables. Add to
this, the use of the set-membership approach to iden-
tify electrical parameters is stimulated by the fact that
the effect of each parasitic parameter appears only in
one segment of the frequency range. That means, for
each frequency segment, the input impedance model
of the studied circuit is significantly simplified and so
the conservativeness related to the set computation is
greatly reduced.
This paper is structured as follows. Section 2
517
Meslem N., Labarre C. and Lecoeuche S..
Using Forward-backward Contractors to Identify Parasitic Parameters of Electrical Circuits Working in High Frequency.
DOI: 10.5220/0004040505170522
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 517-522
ISBN: 978-989-8565-21-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

is devoted to state the studied problem and a set-
membership formulation for the parasitic parameters
identification problem is established. In section 3
some definitions and notions about interval analysis
are briefly introduced and thus the principle of con-
tracting a box under set of constraints using interval
analysis is discussed. Our set-membership identifica-
tion algorithm is presented in section 4 and then sim-
ulated test is included to illustrate the merits of this
approach.
2 PROBLEM STATEMENT
The aim of the paper consists in estimating the par-
asitic parameters associated to passive electrical cir-
cuits working in high frequency. Before presenting a
set-membership formulation for our parameters iden-
tification problem, let us briefly recall the definition
of the input impedance concept of electrical circuit.
In fact, the input impedance of an electrical circuit is
the equivalent impedance seen by a power source con-
nected to that circuit. If the source provides known
voltage and current, such impedance can be calcu-
lated using Ohm’s law. In practice, the observed be-
haviors of electrical components are usually different
from those described by the theoretical laws. For in-
stance, the real behavior of a simple capacitor seems
like the behavior of a theoretical RLC series circuit
where the capacitance is given by the manufacturer.
As well, the real behavior of a simple coil is modeled
by a resistor connected in series with an inductance
and both are connected in parallel with a capacitor
where the value of the inductance is known, see Fig-
ure 1. Hereafter, we denote by p the parameter vector
C
L
( )a
( )b
L
l
R
l
C
c
R
c
L
C
Ê Ê Ê Ê Ê
Ê Ê Ê Ê
Ê Ê Ê Ê
Ê
Figure 1: (a) Ideal case, (b) Real case, where R
c
, L
c
, R
l
and C
l
are the parasitic parameters and L, C are the known
parameters.
that contains all the parasitic parameters associated to
a given circuit and let Z(p,w) be its input impedance
model. Then, our purpose consists in characterizing
in guaranteed way the following set of parameters
P =
p ∈ D | ∀i = 1,...,N, Z(p,w
i
) ∈ Z
i
(1)
where Z
i
is the feasible domain of the measured in-
put impedance at the frequency F
i
(w
i
= 2πF
i
) and D
is the initial research space of parameters. Note that,
here the guarantee term means that no consistent pa-
rameters can be lost during the pruning phase. Now,
assume that for all i ∈ {1,..., N} the feasible domain
of measurement Z
i
is built as follows
Z
i
= Z
i
+ E
i
(2)
where Z
i
represents the real measurement and E
i
rep-
resents the feasible domain of error, which includes
both modeling and measurement error. To reach our
goal, in the unknown but bounded error framework,
we will use a set-membership approach based on in-
terval analysis (Jaulin et al., 2001). Note that, this
approach tries to compute a tighter outer approxima-
tion [p] of the parameters set (1). That is [p] contains
all the elements of the set P ([p] ⊇ P). In the next,
before presenting our identification algorithm, we in-
troduce some definitions and tools of interval analysis
(Moore, 1966).
3 INTERVAL ANALYSIS
Interval analysis was initially developed to account
for the quantification errors introduced by the floating
point representation of real numbers with computers
and was extended to reliable computations (Moore,
1966). Denote by [x] = [x,x] a real interval which is a
connected and closed subset of R where the real num-
bers x and x are respectively the lower and the upper
bound of [x]. So, the set of all real intervals of R is
denoted by IR. Over IR an interval arithmetic was
built by an extension of the real arithmetic operations.
That means, for each operator ◦ ∈ {+, −, ×, ÷} and
for each couple of intervals [x] and [y] one defines
[x] ◦ [y] = {a ◦ b | a ∈ [x], b ∈ [y]} (3)
The width of an interval [x] is defined by w([x]) =
x − x. As well, an interval vector or box denoted
by [x] is a subset of R
n
defined as the Cartesian
product of n closed intervals. The set of all inter-
val vectors of order n will be denoted by IR
n
. The
width of an interval vector of dimension n is defined
by w([x]) = max
1≤i≤n
w([x
i
]). Likewise, we define
the vector width of an interval vector by w
v
[x]
=
w([x
1
]),w([x
2
]),...,w([x
n
])
. That means the com-
ponents of the real vector w
v
are the widths of each
component of the interval vector [x].
3.1 Inclusion Functions
Consider the real function f : R
n
→ R. The range of
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
518

this function over an interval vector [x] is given by:
f ([x]) = { f (a) | a ∈ [x]} (4)
Then, one calls an inclusion function denoted by [ f ]
for the real function f an interval application that sat-
isfies the following inclusion
∀[x] ∈ IR
n
, f ([x]) ⊂ [ f ]([x]) (5)
In practice, the simplest manner to obtain an inclusion
function [ f ] for real function f consists in replacing
each occurrence of a real variable by the correspond-
ing interval and each standard function by its inter-
val counterpart. The resulting function is called the
natural inclusion function and the tightness of the en-
closure provided by [ f ] depends on the formal expres-
sion of f . In fact, it is well known if the same variable
x
i
has many occurrences in the mathematical expres-
sion of f , the dependence effect (Moore, 1966) (Jaulin
et al., 2001) will induce pessimism while computing
an enclosure of the range of the real function. Hence,
formal pre-processing of the function expression is
advisable in order to minimize the number of variable
occurrences. In the next paragraph, we will show how
thanks to interval computation one can solve easily
some constraint satisfaction problems (CSP) for con-
tinuous domains (Jaulin et al., 2001).
3.2 Constraint Satisfaction Problem
Historically the constraint satisfaction problems were
firstly formulated and studied in the context of dis-
crete domains, viz the variables belonged to finite sets
(Mackworth, 1977). Then, they have been extended
to continuous domains where the variables are part of
subsets of R or intervals (Sam-Haroud and Faltings,
1996). In continuous setting one defines a CSP as fol-
lows
H : (g(x) = y, x ∈ [x],y ∈ [y]) (6)
where the vectors x and y belong respectively to R
n
and R
m
with n not necessarily equal to m. Further-
more, the set of constraints can be assimilated to a
subset S of R
n
defined by
S = {x ∈ [x] | g(x) ∈ [y]} (7)
In practice, thanks to special algorithms (contractors)
(Jaulin et al., 2001) based on interval analysis and
consistency techniques, one can get with a polyno-
mial complexity in time and space, an outer approx-
imation S of the solution set S ⊆ S. Moreover, the
outer approximation set S is said global and guaran-
teed in the sense that it encloses all the possible so-
lutions of the CSP H . Thus, contracting an interval
vector (box) [x] under the set of constraints H con-
sists in computing a smaller box [x
0
], which contains
in guaranteed way the set resulting from the follow-
ing intersection S ∩ [x] ⊂ [x
0
]. That means, one at-
tempts to reduce the width of the initial box [x] ac-
cording to the set of constraints H . In the literature
several types of contractors are developed in order to
deal with specific CSP. For instance, we can cite those
inspired from point algorithms such as Gauss elimina-
tion, Gauss-Seidel algorithm, Krawczyk method, lin-
ear programming and Newton algorithm (Jaulin et al.,
2001). Hereafter, let C be a contractor and note that
all contractors have the following properties:
∀[x], C ([x]) ⊂ [x] (contractance),
∀[x], [x] ∩ S ⊂ C ([x]) (correctness),
[x] ⊂ [y] ⇒ C ([x]) ⊂ C ([y]) (monotonicity)
(8)
and a fixed point of a contractor C is a box [x] such
that C ([x]) = [x]. To close this section, we present
in the following a contractor based on the forward-
backward constraint propagation.
3.3 Forward-backward Contractor
In this paragraph, we illustrate the core idea of con-
tracting a box [x] according to a set defined by H
using the constraints propagation on intervals (Ben-
hamou et al., 1999). Note that, for the kind of
contractor the dimension of the vector function g
is no longer necessarily equal to the dimension of
the variable vector x. Assume that the mathemati-
cal expression g(x) = y is decomposable into a se-
quence of primitive constraints. Roughly speak-
ing, a primitive constraint is a constraint involving
only a single operator {+,−,×,÷} or single func-
tion {sin,cos,exp,...}. The forward-backward con-
tractor, here denoted by C
f b
, incorporates two proce-
dures called forward propagation and backward prop-
agation. Using interval computation, a direct evalua-
tion of all the primitive constraints are achieved in the
forward propagation procedure in order to obtain in
a sequential way an inclusion function for g. Then,
using consistency techniques (Sam-Haroud and Falt-
ings, 1996) the width of the computed inclusion func-
tion is reduced in accordance with the given box [y].
After this correction a backward propagation is per-
formed from the corrected inclusion function to its
elementary arguments gathered in the interval vector
[x]. Now, let us explain how works this kind of con-
tractor through a simple example. Consider the non-
linear constraint
g(x
1
,x
2
) = x
1
exp(x
2
) = y, (x
1
,x
2
) ∈ [x
1
]×[x
2
], y ∈ [Y ]
(9)
which can be decomposed into sequence of two prim-
itive constraints
a
1
= exp(x
2
)
y = x
1
a
1
(10)
UsingForward-backwardContractorstoIdentifyParasiticParametersofElectricalCircuitsWorkinginHighFrequency
519

where a
1
is an intermediate variable. Then the for-
ward propagation is obtained by an intervalization of
the point sequence (10) as follows
[a
1
] = exp([x
2
])
[y] = [x
1
] ∗ [a
1
]
(11)
The correction stage consists in reducing the size of
[y] by eliminating its inconsistent part with [Y ]. That
means, one computes the following intersection
[y] = [Y ] ∩ [y] (12)
Thus, from the corrected box [y], the backward propa-
gation computes the interval variables [x
1
] and [x
2
] in
the following way
[a
1
] = [y]/[x
1
] ∩ [a
1
]
[x
1
] = [y]/[a
1
] ∩ [x
1
]
[x
2
] = log([a
1
]) ∩ [x
2
]
(13)
To resume, the algorithm below gives the finite list of
instructions that must be performed by the forward-
backward contractor C
f b
to get an outer approxima-
tion of the solution set of (9).
Algorithm. C
f b
([x
1
],[x
2
],g,[Y ])
1. Forward Propagation
• [a
1
] := exp([x
2
])
• [y] := [x
1
] ∗ [a
1
]
2. Correction
• [y] := [Y ] ∩ [y]
3. Backward Propagation
• [a
1
] := [y]/[x
1
] ∩ [a
1
]
• [x
1
] := [y]/[a
1
] ∩ [x
1
]
• [x
2
] := log([a
1
]) ∩ [x
2
]
4. Return ([x
1
],[x
2
])
Thus, in the next section, using the forward-backward
contractor we design a new set-membership algorithm
to estimate the parasitic parameters associated to elec-
trical components working in high frequency.
4 ESTIMATION ALGORITHM
Recall that our purpose consists in developing a spe-
cific algorithm that is able to identify all the parasitic
parameters that appear in electrical circuits. In other
terms, we want to build more realistic models for elec-
trical circuits in order to well understand the undesir-
able EMI effects. To do so, we propose to measure for
several frequencies the input impedance of the stud-
ied circuit working in different configurations. For in-
stance, we consider the open circuit (o), the short cir-
cuit (s) and the closed circuit (c) configurations. Then,
for each measured impedance we apply the forward-
backward contractor. To be more clear, let us assume
that for each configuration we measure the real and
the imaginary parts of the input impedance. That is,
at each frequency measurement F
i
,i ∈ {1,...,N}, we
have
Z
m
i
= R
m
i
+ jI
m
i
(14)
where m ∈ {c, o, s} and R
m
i
, I
m
i
represent respectively
the real and the imaginary parts of the measured input
impedance. The feasible domains of measurements
are given by
R
m
i
= R
m
i
+ E
R
i
, I
m
i
= I
m
i
+ E
I
i
(15)
here E
R
i
and E
I
i
represent the priori known feasible
domains of error. Then, we want to determine a tight
outer approximation of the following set of parame-
ters
P =
p ∈ D |
∀m ∈ {c,o,s}, ∀i ∈ {1,.. .,N}
(R
m
(p,w
i
) ∈ R
m
i
) ∧ (I
m
(p,w
i
) ∈ I
m
i
)
(16)
where R
m
(p,w) and I
m
(p,w) represent respectively
the real and the imaginary part of the input impedance
models
Z
m
(p,w) = R
m
(p,w
i
) + jI
m
(p,w) (17)
Moreover, the above parameters set (16) is also
defined by the following CSP
H :
∀m ∈ {c,o,s}, ∀i ∈ {1,.. .,N}
R
m
(p,w
i
) = R
m
i
, p ∈ D, R
m
i
∈ R
m
i
∧
I
m
(p,w
i
) = I
m
i
, p ∈ D, I
m
i
∈ I
m
i
(18)
Then, based on the forward-backward contractor,
the algorithm below gives the procedure to be fol-
lowed for computing an outer approximation of the
set of parameters (16).
Algorithm. SM-Ident(Input: D, Output: [p])
[p] := D
ε
1
:= w
v
([p])
ε
2
:= 0.9 ∗ ε
1
while (ε
2
< ε
1
)
ε
1
:= w
v
([p])
for m := o,s,c
while (ε
2
< ε
1
)
ε
1
:= w
v
([p])
for i := 1,..., N
R
m
i
:= R
m
i
+ E
R
i
[p] := C
f b
[p],R
m
(p,w
i
),R
m
i
I
m
i
:= I
m
i
+ E
I
i
[p] := C
f b
[p],I
m
(p,w
i
),I
m
i
end
ε
2
:= w
v
([p])
end
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
520
end
ε
2
:= w
v
([p])
end
Remark. For this algorithm the comparison operator
< applied between real vectors should be understood
as a collection of inequalities applied component by
component.
For a given initial research space of parame-
ters D, the SM-Ident algorithm uses the forward-
backward contractors to reduce its size throughout
several stages. Indeed,
• for each experience: the open circuit, the short cir-
cuit and the closed circuit configuration (ordered
by the first for loop),
• for each value of the measured input impedance
(14) with its feasible domain (15) (ordered by the
second for loop),
the forward-backward contractor is applied succes-
sively to reduce [p] under the constraints defined by
the real and imaginary parts of the input impedance
model (17). Thus, the box contracting procedure is
repeated until no size reduction is observed. That
means, the real width vector w
v
becomes constant,
and so one leave the two while loops.
4.1 Discussion about Pessimism
In fact, in the field of system identification, it is well
known that the applied interval methods suffer from
pessimism generated by the dependence phenomenon
of interval computation (Moore, 1966) (Jaulin et al.,
2001). Therefore, the use of interval approach to
solve practical problems is limited. In this para-
graph, we try to explain why we claim that in the
case of electrical circuits the interval identification ap-
proaches give good results.
In practice, when we analyze the behavior of the
input impedance of an electrical circuit, we find that
the effect of each passive element of the studied cir-
cuit is significant only on a well defined frequency
range. This fact is justified by the following proper-
ties: (i) each coil of the circuit behaves as a low pass
filter with a specific cutoff frequency; (ii) each capac-
itor of the circuit behaves as a high pass filter with
a specific cutoff frequency; (iii) the impedance of an
RLC circuit in resonance is equal to its resistance. Ac-
cording to these properties, we can safely conclude
that on each frequency segment, the impedance model
of the studied circuit is significantly simplified and so
the conservativeness related to the pessimism of set
computation is greatly reduced even if the impedance
model contains unknown parameters with many oc-
currences.
To illustrate the merits of our estimation method,
the next subsection is devoted to its application to
identify the parasitic parameters associated to a sim-
ple second order electrical filter.
4.2 Illustrative Example
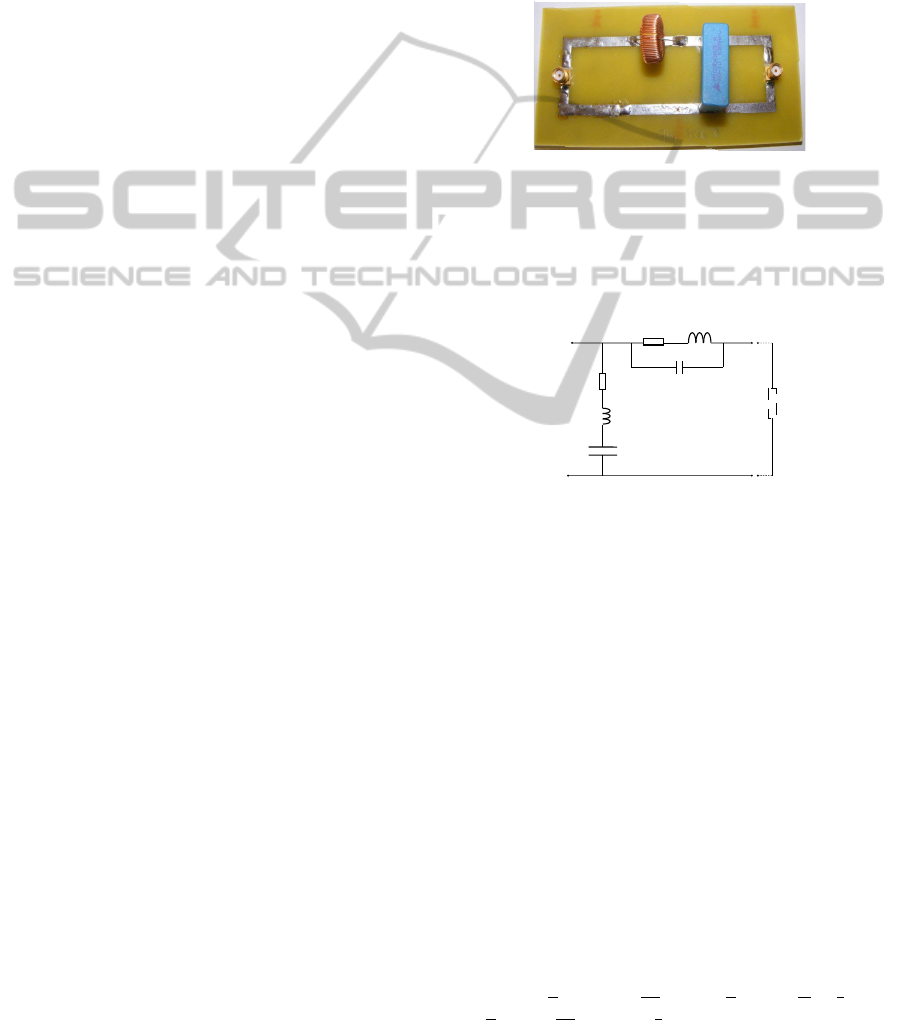
Consider the electrical second order filter depicted in
Figure 2.
Ê Ê Ê Ê Ê
Ê Ê Ê Ê
Ê Ê Ê Ê
Ê
Figure 2: Real second order filter constituted by a capacitor
with capacitance C = 1µF and a coil with inductance L =
300µH.
Taking into account the physical existence of the
parasitic parameters, the real filter is equivalent to the
circuit depicted in Figure 3. For our experience, we
(p, )
Z
w
C
c
L
c
R
l
R
l
C
L
R
Ê Ê Ê Ê Ê
Ê Ê Ê Ê
Ê Ê Ê Ê
Ê
Figure 3: A more realistic model for the second order filter.
assume that the values of the main components L and
C are well known L = 300µH and C = 1µF. Then, we
attempt to estimate the vector p = [R
c
,L
c
,R
l
,C
l
]. To
do that, we will use the SM-Ident algorithm. The ex-
perimental data are collected from three experiences:
the open circuit, the short circuit and the closed cir-
cuit experiences. Note that, for the last case we close
the circuit by a resistive load R = 50Ω and for each
experience the real and imaginary parts of the input
impedance are measured for several frequencies.
As shown previously, the basic components of
the SM-Ident algorithm are the forward-backward
contractors C
f b
. To design these contractors, we
must compute the analytical expressions of the in-
put impedances. For instance, in the case of short
circuit experience, by direct computation we obtain
the following expression of the real part of the input
impedance
R
s
(p,w) = (AC + BD)/(C
2
+ D
2
) (19)
where A =
1
C
l
LR
c
+ (L
c
−
1
Cw
2
)R
l
, B =
1
C
l
L(L
c
w −
1
Cw
) −
1
w
R
l
R
c
,
C =
1
C
l
(L + L
c
−
1
Cw
2
) + R
l
R
c
+ L(
1
C
− L
c
w
2
) and D = R
c
Lw + R
l
(L
c
w −
UsingForward-backwardContractorstoIdentifyParasiticParametersofElectricalCircuitsWorkinginHighFrequency
521

1
Cw
)−
1
C
l
w
(R
c
+R
l
). Thus, we have to resolve at each mea-
surement the following CSP
R
s
(p,w
i
) = R
s
i
, p ∈ [p],R
s
i
∈ R
s
i
To do that, we use (19) to build a contractor as il-
lustrated in subsection 3.3. Similarly, for each ex-
perience we build contractors for the real and imag-
inary parts of the input impedance. So, all ingredients
needed to use SM-Ident algorithm are available. In
following a simulation test is achieved to show the
performances of the SM-Ident algorithm.
4.3 Simulation Test
For each circuit configuration, m ∈ {o,s,c}, the sim-
ulated data are obtained by using the analytical ex-
pression of the input impedance Z
m
(p
∗
,w) with p
∗
=
[85mΩ,43µH,150mΩ,1pF]. Thus, for a discrete
set of frequencies {F
1
,F
2
,F
3
,...,F
N
} where ∀i ∈
{1,...,N}, F
i
∈ [10, 10G]Hz, we build the simulated
measurement signals (R
m
i
,I
m
i
) with their feasible do-
mains,
R
m
i
= R
m
i
+ [−ε,ε]|R
m
i
|, I
m
i
= I
m
i
+ [−ε,ε]|I
m
i
|.
where ε is the maximum error that can be disturbed
the measurements. In table 1 some results of the
parameter identification procedure are presented. In
fact, for different values of the maximal error ε
the SM-Ident algorithm contracts the initial research
space of parameters
D =
[0,200]Ω × [0, 6]µH × [0,700]Ω × [0,1]F
until its size will be constant. As shown in table 1,
Table 1: The identified interval parameters.
ε 2% 5% 10%
R
c
(mΩ) [83.3, 86.8] [80.7, 89.3] [76.5, 93.6]
L
c
(ηH) [42.93, 43.07] [42.82, 43.18] [42.65, 43.35]
R
l
(mΩ) [145.2, 154.9] [138.3, 162.3 ] [127.2, 175.1]
C
l
(pF) [0.997, 1.003] [0.992, 1.008 ] [0.985, 1.016]
for each value of ε the sought parameter vector p
∗
is
enclosed in the identified parameter interval vector;
and its accuracy is given by its width. Moreover, the
identified parameter interval vector provides also an
outer approximation of the uncertainty associated to
each identified parasitic parameter. Finally, note that
for initial parameters boxes that do not contain the
sought parameter vector p
∗
, the SM-Ident algorithm
returns as expected an empty set of possible solutions.
5 CONCLUSIONS
In this paper, we developed and tested an identifi-
cation algorithm for electrical circuits modeled by
their input impedance. Our algorithm works in the
unknown-but-bounded-error context and it used in-
terval analysis to solve, in rigorous way, the issue of
parasitic parameters estimation. For future works, we
plan to apply the algorithm to more complex electrical
networks.
ACKNOWLEDGEMENTS
This work was carried out as part of a CPER/ERDF
project funded by the State and the Nord Pas-de-
Calais region.
REFERENCES
Benhamou, F., Goualard, F., Granvilliers, L., and Puget,
J. (1999). Revising hull and box consistency. In
Proceedings of the International Conference on Logic
programming, pages 230–244, The MIT Press.
Buiatti, G., Amaral, A., and Cardoso, A. (2007). An unified
method for estimating the parameters of non-isolated
dc/dc converters using continuous time models. In
Telecommunications Energy Conference, 2007. INT-
ELEC 2007. 29th International, pages 334 –341.
Chen, H., Qian, Z., Zeng, Z., and Wolf, C. (2008). Mod-
eling of parasitic inductive couplings in a pi-shaped
common mode emi filter. Electromagnetic Compati-
bility, IEEE Transactions, 50:71–79.
Jaulin, L., Kieffer, M., Didrit, O., and Walter, E. (2001).
Applied Interval Analysis: with examples in parame-
ter and state estimation, robust control and robotics.
Springer-Verlag, London.
Kotny, J. L., Margueron, X., and Idir, N. (2009). High fre-
quency modeling method of emi filters. In IEEE En-
ergy Conversion Congress and Exposition ECCE’09,
pages 1671 – 1678, San Jose, CA.
Labarre, C. and Costa, F. (2011). Circuit analysis of an emi
filter for the prediction of its magnetic near-field emis-
sions. IEEE Transactions on Electromagnetic Com-
patibility, 99:1–9.
Mackworth, A. (1977). Consistency in networks of rela-
tions. Artificial intelligence, 8:99–118.
Moore, R. (1966). Interval Analysis. Prentice-Hall, Engle-
wood Cliffs.
Sam-Haroud, D. and Faltings, B. (1996). Consistency tech-
niques for continuous constraints. Constraints, 1:85–
118.
Wang, S., Lee, F., and Odendaal, W. (2005). Characteriza-
tion and parasitic extraction of emi filters using scat-
tering parameters. IEEE Transactions on power elec-
tronics, 20:502–510.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
522
