Compensation of Tool Deflection in Robotic-based Milling

Alexandr Klimchik

1,2

, Dmitry Bondarenko

2,3

, Anatol Pashkevich

1,2

Sebastien Briot

and Benôit Furet

2,4

Ecole des Mines de Nantes, 4 Rue Alfred-Kastler, 44307, Nantes, France

Institut de Recherches en Communications et Cybernétique de Nantes, UMR CNRS 6597, Nantes, France

Ecole Centrale de Nantes, 1 Rue de la Noë, 44 321, Nantes, France

Université de Nantes, Quai de Tourville, 44035, Nantes, France

Keywords: Industrial Robot, Milling, Compliance Error Compensation, Dynamic Machining Force Model, Non-linear

Stiffness Model.

Abstract: The paper presents the compliance errors compensation technique for industrial robots, which are used in

milling manufacturing cells. under external loading, which is based on the non-linear stiffness model. In

contrast to previous works, it takes into account the interaction between the milling tool and the workpiece

that depends on the end-effector position, process parameters and cutting conditions (spindle rotation, feed

rate, geometry of the tool, etc.). Within the developed technique, the compensation errors caused by external

loading is based on the non-linear stiffness model and reduces to a proper adjusting of a target trajectory

that is modified in the off-line mode. The advantages and practical significance of the proposed technique

are illustrated by an example that deals with milling with Kuka robot.

1 INTRODUCTION

Currently, robots become more and more popular for

a variety of technological processes, including high-

speed precision machining. For this process, the robot

is subjected by external loading which caused by the

machining force. This force is generated by the inter-

action between the tool mounted on the robot end-

effector and the workpiece during the material re-

moval (Dépincé, 2006). It is a contact force and it is

distributed along the affected area of the tool cutting

part. To evaluate the influence and to analyze the ro-

bot behavior while machining, the cutting force

should be defined either experimentally or using accu-

rate mathematical model.

To evaluate the force caused by interaction be-

tween the tool and the workpiece, two approaches can

be used. The static approach allows computing the

average cutting force without any consideration of

dynamic aspect in machining system. This force

serves as an external loading of the robot. This ap-

proach is widely used in analysis of conventional ma-

chining processes using CNC machines (Altintas,

2000), where the stiffness is high. In contrast, robots

have relatively low structural stiffness. For this rea-

son, in the case of robotic-based machining, an addi-

tional source of dynamic displacements of the end-

effector with respect to the desired trajectory induced

by robot compliance may arise. Such behavior leads

to the variable contact between the machining tool

and the workpiece. Thus, the generated contact force

depends on the current position of the robot end-

effector on the trajectory. Consequently, the cutting

force cannot be evaluated correctly using the static

approach. In this case, the dynamic approach, which

will be used in the paper, is required. It is based on

computing of the force at each instant of machining

process that defines loading of the robot for the next

instant of processing. As a result, the dynamic aspect

of robot motion under such variable cutting force can

be examined for whole process.

Usually, in the robot-based machining this force

causes essential deflections that decrease the quality

of the final product. The problem of the robot error

compensation can be solved in two ways that differ in

degree of modification of the robot control software:

(a) by modification of the manipulator model,

which better suits to the real manipulator and is used

by the robot controller (in simple case, it can be lim-

ited by tuning of the nominal manipulator model, but

113

Klimchik A., Bondarenko D., Pashkevich A., Briot S. and Furet B..

Compensation of Tool Deﬂection in Robotic-based Milling.

DOI: 10.5220/0004040801130122

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 113-122

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

may also involve essential model enhancement by

introducing additional parameters, if it is allowed by

a robot manufacturer);

(b) by modification of the robot control pro-

gram that defines the prescribed trajectory in Carte-

sian space (here, using relevant error model, the input

trajectory is generated in such way that under the

loading the output trajectory coincides with the de-

sired one, while input trajectory differs from the target

one).

Moreover, with regard to the robot-based machin-

ing, there is a solution that does not require

force/torque measurements or computations (Dépincé,

2006), where the target trajectory for the robot con-

troller is modified by applying the "mirror" technique.

An evident advantage of this technique is its applica-

bility to the compensation of all types of the robot er-

rors, including geometrical and compliance ones.

However, this approach requires carrying out addi-

tional preliminary experiments which are quite expen-

sive. So, it is suitable for the large-scale production

only. Another compensation methodology has been

proposed by Eastwood and Webb (Eastwood, 2010)

that was used for gravitational deflection compensa-

tion for hybrid parallel kinematic machines.

This paper focuses on the modification of control

program that is considered to be more realistic in

practice. This approach requires also accurate stiff-

ness model of the manipulator. From point of view of

stiffness analysis, the external and forces directly in-

fluence on the manipulator equilibrium configuration

and, accordingly, may modify the stiffness properties.

So, they must be undoubtedly taken into account

while developing the stiffness model. However, in

most of the related works the Cartesian stiffness ma-

trix has been computed for the nominal configuration

(Chen, 2000; Alici, 2005). Such approach is suitable

for the case of small deflections only. For the opposite

case, the most important results have been obtained in

(Kövecses, 2007; Tyapin, 2009; Pashkevich, 2011),

which deal with the stiffness analysis of manipulators

under the end-point loading.

Thus, to compensate errors caused by the machin-

ing process, it is required to have an accurate stiffness

model and precise cutting force model. In contrast to

the previous works, the compliance error compensa-

tion technique presented in this work is based on the

non-linear stiffness model of the manipulator (Pash-

kevich, 2011) and dynamic model of technological

process that generates the cutting force.

2 PROBLEM STATEMENT

For the compliance errors, the compensation tech-

nique must rely on two components. The first of them

describes distribution of the stiffness properties

throughout the workspace and is defined by the stiff-

ness matrix as a function of the joint coordinates. The

second component describes the forces/torques acting

on the end-effector while the manipulator is perform-

ing its machining task (manipulator loading).

The stiffness matrix required for the compliance

errors compensation highly depends on the robot

configuration and essentially varies throughout the

workspace. From general point of view, full-scale

compensation of the compliance errors requires es-

sential revision of the manipulator model embedded

in the robot controller. In fact, instead of conven-

tional geometrical model that provides inverse/direct

coordinate transformations from the joint to Carte-

sian spaces and vice versa, here it is necessary to

employ the so-called kinetostatic model (Su, 2006).

It is essentially more complicated than the geomet-

rical model and requires rather intensive computa-

tions that are presented in Section 3..

The dynamic behavior of the robot under the load-

ing

F caused by technological process can be de-

scribed as

CC C

+=M δtCδtKδtF

&& &

(1)

where

M is 66

mass matrix that represents the

global behavior of the robot in terms of natural fre-

quencies,

C is 66

damping matrix,

K is 66

Cartesian stiffness matrix of the robot under the ex-

ternal loading

, ,δt δt

and δt

are dynamic dis-

placement, velocity and acceleration of the tool end-

point in a current moment respectively (Briot, 2011).

In general, the cutting force F

has a nonlinear na-

ture and depends on many factors such as cutting

conditions, properties of workpiece material and tool

cutting part, etc (Ritou, 2006). But, for given

tool/workpiece combination, the force F

could be ap-

proximated as a function of an uncut chip thickness h,

which represents the desired thickness to cut at each

instant of machining.

Hence, to reduce errors caused by cutting forces in

the robotic-based machining it is required to obtain an

accurate elasto-static model of robot and elasto-

dynamic model of machining process. These prob-

lems are addressed in the following sections taking

into account some particularities of the considered

application (robotic-based milling).

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

114

3 MANIPULATOR MODEL

3.1 Elasto-Static Model

Elasto-static model of a serial robot is usually de-

fined by its Cartesian stiffness matrix, which should

be computed in the neighborhood of loaded configu-

ration. Let us propose numerical technique for com-

puting static equilibrium configuration for a general

type of serial manipulator. Such manipulator may be

approximated as a set of rigid links and virtual

joints, which take into account elasto-static proper-

ties (Figure 1). Since the link weight of serial robots

is not negligible, it is reasonable to decompose it in-

to two parts (based on the link mass centre) and ap-

ply them to the both ends of the link. All this load-

ings will be aggregated in a vector

[

]

...

=GGG,

where

G is the loading applied to the i-th node-

point. Besides, it is assumed that the external load-

ing

F (caused by the interaction of the tool and the

workpiece) is applied to the robot end-effector.

Figure 1: VJM model of industrial robot with end-point

and auxiliary loading.

Following the principle of virtual work, the work

of external forces

,GF is equal to the work of inter-

nal forces

τ caused by displacement of the virtual

springs

δθ

()

TTT

δδδ

j =

⋅+⋅=⋅

∑

GtFtτθ (2)

where the virtual displacements

t can be comput-

ed from the linearized geometrical model derived

from

()

δδ,1..

jn==tJθ , which includes the Jaco-

bian matrices

(

)

()

=∂ ∂Jgqθθ with respect to

the virtual joint coordinates.

So, expression (2) can be rewritten as

()()

T() T() T

θθθ

δδδ

⋅⋅+⋅⋅=⋅

∑

GJ θ FJ θτ θ (3)

which has to be satisfied for any variation of

δθ . It

means that the terms regrouping the variables

δθ

have the coefficients equal to zero. Hence the force

balance equations can be written as

()T ()T

θθ θ

⋅+ ⋅

∑

τ JGJF (4)

These equations can be re-written in block-matrix

form as

(G)T (F)T

θθ θ

⋅+ ⋅τ JGJF (5)

where

(F) ( )

θθ

=JJ,

(G) (1) ( )

θθθ

...

⎡⎤

⎣⎦

JJJ

...

⎡

⎤

⎣

⎦

GGG

. Finally, taking into account the

virtual spring reaction

θθ

=⋅τ K θ , where

(

)

θθθ

,...,diag=KKK, the desired static equilibri-

um equations can be presented as

(G)T (F)T

θθ θ

⋅

+⋅=⋅JGJFKθ (6)

To obtain a relation between the external loading

F and internal coordinates of the kinematic chain θ

corresponding to the static equilibrium, equations (6)

should be solved either for different given values of

F or for different given values of t . Let us solve the

static equilibrium equations with respect to the ma-

nipulator configuration

θ and the external loading

for given end-effector position

()

=tgθ and the

function of auxiliary-loadings

()

G θ

() ()

(G)T (F)T

θθ θ

;;⋅= + = =K θ JGJFt

θ GGθ (7)

where the unknown variables are

()

,θ F .

Since usually this system has no analytical solu-

tion, iterative numerical technique can be applied. So,

the kinematic equations may be linearized in the

neighborhood of the current configuration

(

)

(

)( )

(F)

θ11

;

ii iii++

=+ ⋅−tgθ J θθ θ (8)

where the subscript '

i' indicates the iteration number

and the changes in Jacobians

(G) (F)

θθ

,JJ

and the auxil-

iary loadings

G are assumed to be negligible from

iteration to iteration. Correspondingly, the static

equilibrium equations in the neighborhood of

may be rewritten as

(G)T (F)T

θ 1θ 1 θ

⋅

+⋅=⋅JGJFKθ

. (9)

Thus, combining (8), (9) and analytical expression

for

1(G)T (F)T

θθ θ

()

−

⋅+ ⋅θ KJ GJ F, the unknown varia-

bles

F and θ can be computed using following itera-

tive scheme

CompensationofToolDeflectioninRobotic-basedMilling

115

()

(F) 1 (F)T

θθ

(F) (F) 1 (G)T

θθ θ

1(G)T (F)T

θθ

1θ1

ii i i

iii

−

=⋅⋅

−+−

=⋅+⋅

FJKJ

tgθ J θ JK J G

θ KJ GJ F

(10)

The proposed algorithm allows us to compute the

static equilibrium configuration for the serial robot

under external loadings applied to any point of the

manipulator and the loading from the technological

process.

3.2 Stiffness Matrix

In order to obtain the Cartesian stiffness matrix, let

us linearize the force-deflection relation in the

neighborhood of the equilibrium. Following this ap-

proach, two equilibriums that correspond to the ma-

nipulator state variables

(, ,)F θ t and

( δ , δ , δ )+++FFθθtt should be considered simul-

taneously. Here, notations

δF , δt define small in-

crements of the external loading and relevant dis-

placement of the end-point. Finally, the static equi-

librium equations may be written as

()

(G)T (F)T

θθ θ

;=⋅=⋅+⋅tgθ K θ JGJF (11)

and

()

(G) (G)

θθθ

(F) (F)

θθ

δδ

δδ δ

δδ

+= +

⋅+ = + ⋅ +

++ ⋅+

ttgθθ

K θθ JJ GG

JJ FF

(12)

where

,,, ,tFGK θ are assumed to be known.

After linearization of the function

()g θ in the

neighborhood of the loaded equilibrium, the system

(11), (12) is reduced to equations

(F)

(G) (G) (F) (F)

θθθ θθ

δδ

δδ δ δ δ

⋅= + + +

tJ θ

K θ JGJ G JFJ F

(13)

which defines the desired linear relations between

δt and δF . In this system, small variations of Jaco-

bians may be expressed via the second order deriva-

tives

(F) (F)

θθθ

δδ=⋅JHθ ,

(G) (G)

θθθ

δδ=⋅JHθ , where

(G) 2

θθ

=∂ ∂

∑

HgGθ ,

θθ

2)2T

=∂ ∂HgFθ . Al-

so, the auxiliary loading

G may be computed via

the first order derivatives as

δδ=∂ ∂ ⋅GGθθ

Further, let us introduce additional notation

(F) (G) (G)T

θθ θθ θθ θ

=++ ⋅∂∂HHH J Gθ

, which allows us to

present system (13) in the form

(F)

(F)T

θθθθ

δδ

⎡⎤

⎡

⎤⎡⎤

=⋅

⎢⎥

⎢

⎥⎢⎥

−+

⎣

⎦⎣⎦

⎣⎦

0 θ

JKH

(14)

So, the desired Cartesian stiffness matrices

K can

be computed as

(

)

(F) 1 (F)T

C θθ θθθ

()

−

=−KJKHJ (15)

Below, this expression will be used for computing of

the elasto-static deflections of the robotic manipula-

tor.

3.3 Mass Matrix

To evaluate dynamic behaviour of the robot under

the loading, in addition to the Cartesian stiffness ma-

trix

K it is required to define the mass matrix

M .

Comprehensive analysis and definition of this matrix

have been proposed in (Briot, 2011). Here, let us

summarise the main results that will be used further

in the error compensation technique.

Similar to the stiffness matrix, here physical prop-

erties defined by the mass matrix

M are constant in

the joint coordinates

const

M and are defined by

the mass matrices

θi

M of all n links of the robot

θθ1 θn

( ,..., )diag

MMM. Assuming that link may be

approximated by a beam with a constant cross-

section, the mass matrix

θi

M can be computed as

θ 123456

(, , , , , )

diag a a a a a a

M (16)

where

33 /140

am= ,

iii

aIL

= ,

8/15

iii

aIL

= ,

8/15

iii

aIL

= ,

m is physical mass of i-th link,

is density of i-th

link,

L is link length,

is the polar moment,

are the second moments of the area. Since the

mass matrix

M is defined in the joint coordinates it

can be recomputed into the Cartesian coordinates

associated with the tool end-point using the Jacobian

matrix

J (which depend on the robot configuration

q and computed with respect to virtual joint coordi-

nates

θ ) using following expression

θC θθ

=MJMJ (17)

Thus, using expressions (16) and (17) it is possible

to compute the mass matrix

M for a given robot

configuration

q .

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

116

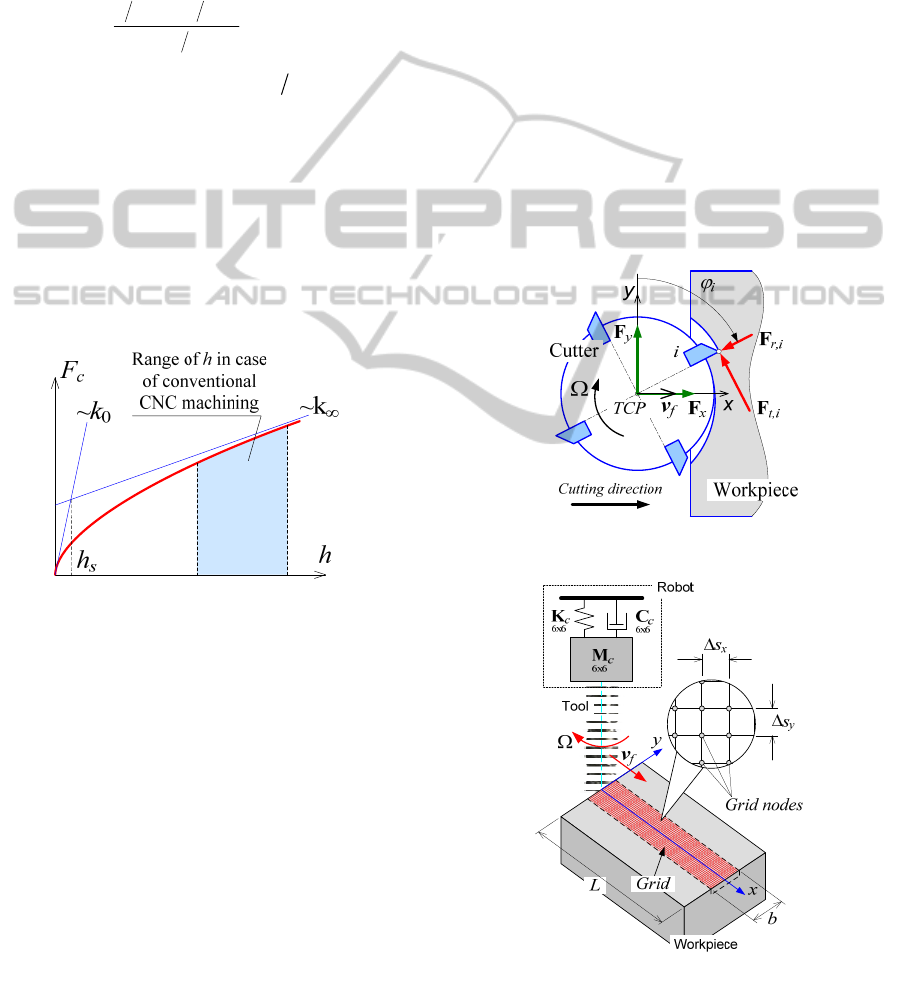
4 MACHINING PROCESS

Let us obtain the model of the cutting force which de-

pends on the relative position of the tool with respect

to the workpiece at each instant of machining. As fol-

lows from previous works (Brissaud, 2008), for the

known chip thickness

h, the cutting force F

can be

expresses as

()

hh r hh

Fh k a h

=≥

(18)

where

a is a depth of cut,

1rkk

∞

=< depends

on the parameters

∞

, k

that define the so called

stiffness of the cutting process for large and small

chip thickness

h respectively (Figure 2) and h

is a

specific chip thickness, which depends on the cur-

rent state of the tool cutting edge. The parameters

, r are evaluated experimentally for a given com-

bination of tool/working material. To take into ac-

count the possible loss of contact between the tool

and the workpiece, expression (18) should be sup-

plement by the case of

Figure 2: Fractional cutting force model F

(h).

()

0, if 0

Fh h=< (19)

For the multi-edge tool the machining surface is

formed by means of several edges simultaneously.

The number of working edges varies during machin-

ing and depends on the width of cut. For this reason,

the total force

of such interaction is a superposition

of forces

c,i

generated by each tool edge i, which are

currently in the contact with the workpiece. Besides,

the contact force

c,i

can be decomposed by its radial

r,i

and tangential F

t,i

components (Figure 3). In ac-

cordance with Merchant’s model (Merchant, 1945),

the

t-component of cutting force F

t,i

can be computed

with the equation (18). The

r-component F

r,i

is related

with

t,i

by following expression (Laporte 2009)

,,ri r ti

kF= (20)

where the ratio factor

depends on the given

tool/workpiece characteristics.

It should be mentioned that in robotic machining it

is more suitable to operate with forces expressed in

the robot tool frame {

x,y,z}. Then, the corresponding

components

, F

(Figure 3) of the cutting force F

can be expressed as follows

cos sin

sin cos

ri i ti i

yriitii

FF F

=− +

∑∑

(21)

where

is the number of currently working cutting

edges,

is the angular position of the i-th cutting

edge (the cutting force in

z direction F

is negligible

here). So, the vector of external loading of the robot

due to the machining process can be composed in

the frame {

x,y,z} using the defined components F

as F=[F

,0,0,0,0]

Figure 3: Forces of tool/workpiece interaction.

Figure 4: Meshing of the workpiece area.

It should be stressed that the cutting force compo-

CompensationofToolDeflectioninRobotic-basedMilling

117

nents

r,i

, F

t,i

mentioned in equation (18),(20) are

computed for the given chip thickness h

, which

should be also evaluated. Let us define model for

using mechanical approach. Then the chip thickness

removed by

i-th tooth depends on the angular position

of this tooth and it can be evaluated using to the

geometrical distance between the position of the given

tooth

i and the current machining profile (Figure 3). It

should be mentioned, that the main issue here is to

follow the current relative position between the

i-th

tooth and the working material or to define whether

the

i-th tooth is involved in cutting for given instant of

process. Because of the robot dynamic behavior and

the regenerative mechanism of surface formation

(Tlusty, 1981) this problem cannot be solved directly

using kinematic relations. In this case it is reasonable

to introduce a special rectangular grid, which decom-

poses the workpiece area into segments and allows

tracking the tool/workpiece interaction and the for-

mation of the machining profile (Figure 4).

Here, Steps Δ

, Δs

between grid nodes are con-

stant and depend on the tool geometry, cutting condi-

tion and time discretization Δ

τ. Each node j

(

jN= , N

is the number of nodes) of the grid can

be marked as “1” or “0”: “1” corresponds to nodes

situated in the workpiece area with material (rose

nodes in 0), “0” corresponds to nodes situated in

workpiece area that was cut away (white nodes in 0).

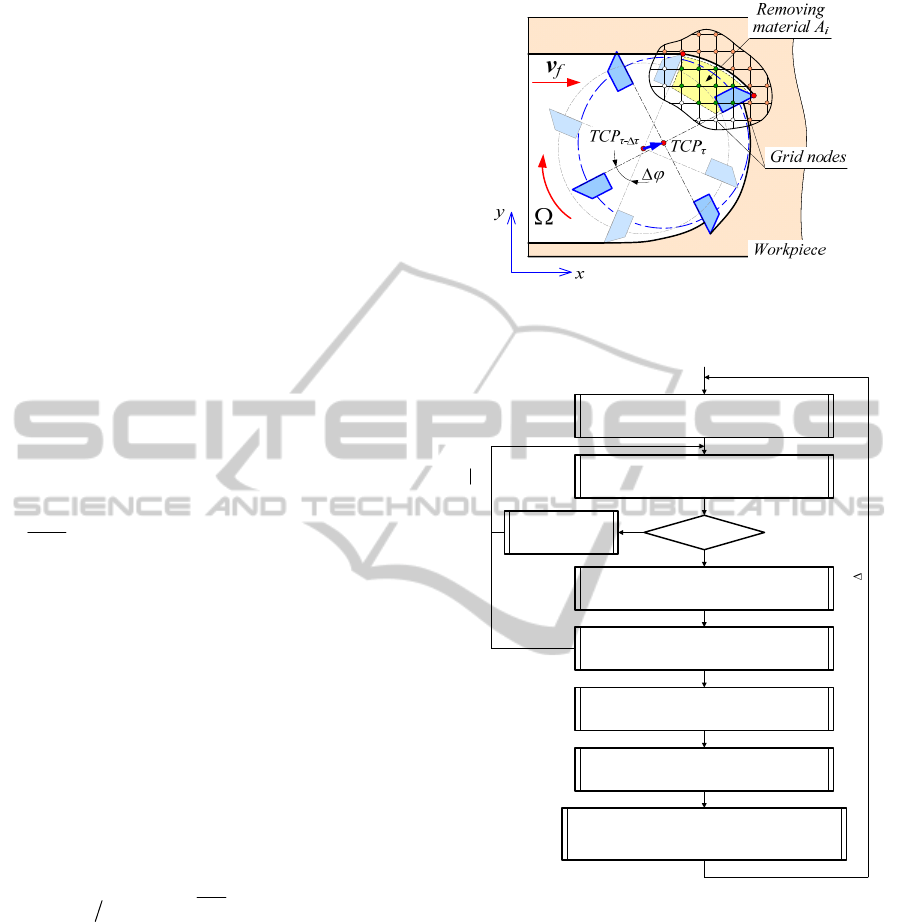
In order to define the number of currently cut

nodes by the

i-th tooth, the previous instant of ma-

chining process should be considered. Let us define

as an amount of working material that is currently cut

away by the

i-th tooth (Figure 5). So, if node j marked

as “1” is located inside the marked sector (green

nodes in Figure 5), it changes to “0” and

is increas-

ing by

sΔΔ . Analyzing all potential nodes and

computing

, the chip thickness h

, removed at given

instant of the process by the

i-th tooth, can be estimat-

ed by

ii i

hAR

=Δ

iN=

. The angle Δφ

deter-

mines the current angular position of the

i-th tooth

regarding to its position at the instant

τ-Δτ and re-

ferred to the position of TCP at

τ-Δτ.

Described mechanism of chip formation and the

machining force model (18) allow computing the dy-

namic behavior of the robotic machining process

where models of robot inertia and stiffness are dis-

cussed in the section 3 of the paper. The detailed algo-

rithm that is used in numerical analysis is presented in

Figure 6, where the analysis of the robot dynamics is

performed in the tool frame with respect to the dy-

namic displacement of the tool

δt

dyn

fixed on the robot

end-effector around its position on the trajectory..

Figure 5: Evaluating the tool/workpiece intersection A

and computing the corresponding chip thickness h

Computing the position of TCP and position/

orientation of all teeth (tool frame)

Analysis of interaction between j-th tooth and

grid nodes, computing A

Updating the grid, computing the chip

thickness h

Definition of the external loading caused by

technological process (tool frame) :

F=[F

0 0 0 0]

Repeat for all teeth

Yes

Zero cutting

forces, F

=0, F

Computing the radial and tangential cutting

force components F

, F

Computing the machining forces F

, F

(tool

frame)

Analysis of dynamics of the robotic machining

process (tool frame)

Next time step τ : τ=τ

: τ:τ

MAX

Zj ,1=

11 1

dyn c c dyn c c dyn c

−− −

=− − +δtMCδtMKδtMF

&& &

Figure 6: Algorithm for numerical simulation of robotic

machining process dynamics.

5 COMPLIANCE ERROR

COMPENSATION TECHNIQUE

In industrial robotic controllers, the manipulator mo-

tions are usually generated using the inverse kine-

matic model that allows us to compute the input sig-

nals for actuators

ρ corresponding to the desired

end-effector location

t , which is assigned assum-

ing that the compliance errors are negligible. How-

ever, if the external loading

F is essential, the kin-

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

118

ematic control becomes non-applicable because of

changes in the end-effector location. It can be com-

puted from the non-linear compliance model as

(

)

−

=tFt (22)

where the subscripts 'F' and '0' refer to the loaded

and unloaded modes respectively, and '

| ' separates

arguments and parameters of the function

(

)

f .

Some details concerning this function are given in

our previous publication (Pashkevich, 2011).

To compensate this undeterred end-effector dis-

placement from

t to

t , the target point should be

modified in such a way that, under the loading

F , the

end-platform is located in the desired point

t . This

requirement can be expressed using the stiffness

model in the following way

()

(F)

|f=Ftt (23)

where

(F)

t denotes the modified target location.

Hence, the problem is reduced to the solution of the

nonlinear equation (23) for

(F)

t , while F and

t are

assumed to be given. It is worth mentioning that this

equation completely differs from the equation

(| )f=Ftt, where the unknown variable is t . It

means that here the compliance model does not al-

low us to compute the modified target point

(F)

straightforwardly, while the linear compensation

technique directly operates with Cartesian compli-

ance matrix (Gong, 2000).

To solve equation (23) for

(F)

t , similar numerical

technique can be applied. It yields the following itera-

tive scheme

(

)

(F) (F) 1 (F)

00 0 0

(| )· f

−

=+ −

′

tt t Ft (24)

where the prime corresponds to the next iteration,

(0,1)

∈

is the scalar parameter ensuring the con-

vergence. More detailed presentation of the devel-

oped iterative routines is given in Figure 7.

()

)F(1

| εf

−

−<Ftt

()

1(F)

−

tFt

{

}

{

}

;()

∈=∈ttF0FFt

()

{

}

∈ttFt

{

}

0 j

∈tt

(

)

(F) (F)

00 0

′

⋅

−

tt tt

(F)

()

,,,

iii

qFKθ

Figure 7: Procedure for compensation of compliance er-

rors.

Hence, using the proposed computational tech-

niques, it is possible to compensate a main part

Modified

trajectory

Cartesian

coordinates

Joint

encoders

Joint

coordinates

Cartesian

coordinates

Robot Controller

Actual joint coordinates

Obtained

trajectory

(nominal)

direct

(actual)

Estimated

(nominal)

Error compensator

Joint

coordinates

Desired

trajectory

inverse

Cartesian

coordinates

Modified

trajectory

direct

Cartesian

coordinates

(actual)

Figure 8: Implementation of compliance error compensation technique.

CompensationofToolDeflectioninRobotic-basedMilling

119

compliance errors by proper adjusting the reference

trajectory that is used as an input for robotic control-

ler. In this case, the control is based on the inverse

kinetostatic model (instead of kinematic one) that

takes into account both the manipulator geometry and

elastic properties of its links and joints. Implementa-

tion of developed compliance error compensation

technique presented in Figure 8.

6 EXPERIMENTAL

VERIFICATION

The developed compliance error compensation tech-

nique has been verified experimentally for robotic

milling with the KUKA KR270 robot along a simple

trajectory in aluminum workpiece. It is assumed that

at the beginning of the technological process the robot

is in the configuration

q (see Table 1 Figure 9). The

parameters of the stiffness model for the considered

robot have been identified in (Dumas, 2011) and are

presented in Table 1. Link masses required for the

mass matrix of the robot are presented also in Table 1.

Table 1: Initial data for robotic-based milling.

Joint coordinates, [deg]

90 -50 120 180 25 180

Joint compliances, [rad/N m]*10

-6

0.26 0.15 0.26 1.79 1.52 2.13

Link masses, [kg]

336.8 259.4 85.2 54.5 36.3 18.2

Figure 9: Starting pose of the KUKA KR270 robot to per-

form the operation of milling.

For the milling, the cutter with the external diame-

ter

D=20 mm and four teeth (N

=4) distributed uni-

formly over the tool is used. For the given combina-

tion of the tool and the workpiece material the follow-

ing parameters correspond to the cutting force model

defined in (18):

510×

N/m, h

1.8 10

−

r=0.1, k

=0.3.

Figure 10: Starting relative position of the tool with re-

spect to the workpiece.

0 0.2 0.4 0.6 0.8 1 1.2

100

150

200

250

300

350

0 0.2 0.4 0.6 0.8 1 1.2

-200

-150

-100

-50

100

150

,[N] (workpiece→tool)

τ,[s]

Transient phase of tool engagement

into the workpiece (τ

=0.15s)

(a)

,[N] (workpiece→tool)

τ,[s]

(b)

1 1.005 1.01 1.015 1.02 1.025 1.03

-110

-100

-90

-80

-70

-60

-50

-40

-30

-20

-10

1 1.005 1.01 1.015 1.02 1.025 1.03

170

180

190

200

210

220

230

240

Figure 11: Variation of machining force components F

(a)

and F

(b) for whole milling process.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

120

Taking into account that the workpiece has a

straight borders let us assume that at the instant t=0

one of the teeth of the tool is in contact with the

workpiece material as it is shown in the Figure 10. It

is also assumed that the machining process is per-

forming with the constant feed rate

=4 m/min (ap-

plied in

x-direction of the robot tool frame) and the

constant spindle rotation Ω=8000 rpm along the

straight line of 80 mm. Experimental verification and

numerical simulation of the described case of the

milling process with KUKA KR-270 robot using the

algorithm shown in Figure 6 allows us to trace the

evolution of machining force x,y-components for the

whole process (Figure 11). The corresponding dy-

namic displacement of the tool around its current po-

sition on the trajectory is shown in Figure 12.

0 0.2 0.4 0.6 0.8 1 1.2

-0.04

-0.02

0.02

0.04

0.06

0.08

Figure 12: Evolution of the tool dynamic displacement

δt

dyn

that is composed from x

TCP

and y

TCP

components.



0 0.2 0.4 0.6 0.8 1 1.2

-5

x 10

0 0.2 0.4 0.6 0.8 1 1.2

-4

-2

x 10

-5

, y

TCP

, [mm]

-2

, [m/s]

τ,[s]

TCP

Referenced points

Modified trajectory in y-direction

Referenced points

Modified feed rate in y-direction

Figure 13: Modified trajectory f

and corresponding feed

rate v

in y-direction, computed based on the original dy-

namic displacement of the tool δt

dyn

In accordance with the obtained results the system

robot/machining process realize complex vibratory

motion. The high frequency component of this motion

(about 700 Hz, Figure 11) is related to the spindle ro-

tation and the number of tool teeth

. In certain cases

such behavior can excites the dynamics of the robot

(natural modes) but this study remains out the frame

of the presented paper. On the contrary, the low fre-

quency component of robot/tool motion (about 7 Hz,

Figure 12), especially in the

y-direction (that is per-

pendicular to the applied feed) influences directly the

quality of final product. Such motion is related to the

robot compliance and it can be compensated using the

error compensation technique described in the paper.

Hence, let us form the modified trajectory based on

the dynamic displacement of the robot end-effector in

the

y-direction (Figure 13):

It should be stressed that the time step between

referenced points of this modified trajectory is limited

with the characteristics of the controller used in the

robot (in the presented case this step is chosen 0.05

sec). The corresponding feed rate

for the modified

trajectory has been computed. So, this new data (feed

and feed rate v

) with the data defined in the begin-

ning of this section allow us to compensate the trajec-

tory error during machining caused by the robot com-

pliance. The resulted compensated trajectory in the y-

direction (in time domain) is presented in Figure 14.

0 0.2 0.4 0.6 0.8 1 1.2

-0.02

-0.01

0.01

0.02

TCP

after compensation, [mm]

Figure 14: Evolution of the dynamic displacement ob-

tained after involving the error compensation technique

into the analysis of robotic milling process.

It should be noted that the part of the trajectory

while machining tool is engaging into the workpiece

does not have effect on the quality of final product (sur-

face). During this stage the contact area between the

tool and the workpiece is increasing progressively.

Hence, at each instant of processing the cutter corrects

the machining profile and eliminates trajectory errors

produced during all previous instants. On the contrary,

during the stage of machining with the fully engaged

tool the trajectory in x,y-directions define directly the

final machining profile and this part of trajectory is

analyzed here (Figure 14). Comparison results present-

ed in Figure 12 and Figure 14 are summarized in Table

2. So after applying error compensation technique the

static deviation in y direction has been reduced from

CompensationofToolDeflectioninRobotic-basedMilling

121

0.058 mm to 0.00014 mm (99.8%). Maximum

defilation in the machining profile has been reduced

from 0.063 mm to 0.0047 mm (92.6%). Low frequency

remained the same for both cases.

Table 2: Milling trajectory accuracy before and after com-

pliance error compensation.

Performance measure

Original

trajectory

Modified

trajectory

Low frequency,[ Hz] 6.70 6.70

Static deviation y

, [mm] 58.1e-3 0.14e-3

Max deviation y

MAX

[mm]

63.2e-3 4.70e-3

Hence, obtained results show that the developed com-

pliance error compensation allows us significantly

increase the accuracy of the robotic-based machining.

7 CONCLUSIONS

In robotic-based machining, an interaction between

the workpiece and technological tool causes essential

deflections that significantly decrease the manufactur-

ing accuracy. Relevant compliance errors highly de-

pend on the manipulator configuration and essentially

differ throughout the workspace. Their influence is

especially important for heavy serial robots. To over-

come this difficulty this paper presents a new tech-

nique for compensation of the compliance errors

caused by technological process. In contrast to previ-

ous works, this technique is based on the non-linear

stiffness model and the reduced elasto-dynamic model

of the robotic based milling process.

The advantages and practical significance of the

proposed approach are illustrated by milling with of

KUKA KR270. It is shown that after error compensa-

tion technique significantly increase the accuracy of

milling. In future the proposed technique will be inte-

grated in a software toolbox.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the financial

support of the ANR, France (Project ANR-2010-

SEGI-003-02-COROUSSO) and the Region “Pays de

la Loire”, France.

REFERENCES

Alici G., Shirinzadeh B., 2005. Enhanced stiffness model

ing, identification and characterization for robot manip-

ulators. Proceedings of IEEE Transactions on Robotics,

vol. 21, pp. 554–564.

Altintas Y., 2000. Manufacturing automation, metal cutting

mechanics, machine tool vibrations and CNC design.

Cambridge University Press, New York.

Brissaud D., Gouskov A., Paris H., Tichkiewitch S., 2008.

The Fractional Model for the Determination of the Cut-

ting Forces. Asian Int. J. of Science and Technology -

Production and Manufacturing, vol. 1, pp.17-25.

Briot S., Pashkevich A., Chablat D. Reduced elastodynamic

modelling of parallel robots for the computation of their

natural frequencies. 13th World Congress in Mechanism

and Machine Science, 19 - 25 Juin, 2011, Guanajuato,

Mexico.

Chen S., Kao I., 2000. Conservative Congruence Transfor-

mation for Joint and Cartesian Stiffness Matrices of Ro-

botic Hands and Fingers. The International Journal of

Robotics Research, vol. 19(9), pp. 835–847.

Dépincé P., Hascoët J-Y., 2006. Active integration of tool

deflection effects in end milling. Part 2. Compensation

of tool deflection, International Journal of Machine

Tools and Manufacture, vol. 46, pp. 945-956

Dumas C., Caro S., Garnier S., Furet B., 2011. Joint stiff-

ness identification of six-revolute industrial serial ro-

bots, Robotics and Computer-Integrated Manufactur-

ing, vol. 27(4), pp. 881-888.

Eastwood S. J., Webb P., 2010. A gravitational deflection

compensation strategy for HPKMs, Robotics and Com-

puter-Integrated Manufacturing, vol. 26 pp. 694–702

Gong, C., Yuan J., Ni, J., 2000. Nongeometric error identi-

fication and compensation for robotic system by inverse

calibration. International Journal of Machine Tools &

Manufacture, vol. 40(14) pp. 2119–2137.

Kövecses J., Angeles J., 2007. The stiffness matrix in elas-

tically articulated rigid-body systems. Multibody System

Dynamics. vol. 18(2), pp. 169–184.

Laporte S., K’nevez J.-Y., Cahuc O., Darnis P., 2009. Phe-

nomenological model for drilling operation. Int. J. of

Advanced Manufacturing Technology, vol.40, pp.1-11.

Merchant M. E., 1945. Mechanics of metal cutting process.

I-Orthogonal cutting and type 2 chip. Journal of Applied

Physics, vol.16(5), pp.267–275.

Pashkevich A., Klimchik A., Chablat D., 2011. Enhanced

stiffness modeling of manipulators with passive joints.

Mech. and Machine Theory, vol. 46(5), pp. 662-679.

Ritou M., Garnier S., Furet B., Hascoet J.Y., 2006. A new

versatile in-process monitoring system for milling, Int.

J. of Machine Tools & Manufacture, 46/15:2026-2035.

Tlusty J., Ismail F., 1981, Basic non-linearity in machining

chatter. Annals of CIRP, Vol.30/1, pp.299-304.

Tyapin I., Hovland G., 2009. Kinematic and elastostatic de-

sign optimization of the 3-DOF Gantry-Tau parallel

kinamatic manipulator. Modelling, Identification and

Control, vol. 30(2), pp. 39-56

Su H.-J., McCarthy J. M., 2006. A Polynomial Homotopy

Formulation of the Inverse Static Analyses of Planar

Compliant Mechanisms. Journal of Mechanical Design

vol. 128(4), pp. 776-786.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

122