
A Bug-based Path Planner Guided with Homotopy Classes
Emili Hern
´
andez, Marc Carreras and Pere Ridao
Department of Computer Engineering, University of Girona, 17071 Girona, Spain
Keywords:
Path Planning, Homotopy Classes, Robotics.
Abstract:
This paper proposes a bug-based path planning algorithm guided topologically with homotopy classes. Ho-
motopy classes provide a topological description of how paths avoid obstacles in the workspace. They are
generated with a method we developed, which builds a topological environment based on the workspace that
allows to compute homotopy classes systematically. The homotopy classes are sorted according to a heuristic
estimation of their lower bound. Only those with the smaller lower bound are used to guide the path planner we
propose, called Homotopic Bug (HBug), which efficiently computes paths in the workspace that accomplish
homotopy classes. Results show the feasibility of our method. A comparison with well-known path planners
has also been included.
1 INTRODUCTION
The work presented in this paper is focused on the
design of a navigation system for a robot that is able
to detect the environment, build an internal local map
of the explored area according to the information pro-
vided by the onboard sensors, compute a safe path
through the map and, finally, generate the high-level
commands to follow it. The navigation system has to
be able to generate an Occupancy Grid Map (OGM)
and a path according to the information obtained from
the unknown environment in a reduced amount of
time. The target application of this research project
is autonomous navigation for surveilling and explo-
ration tasks in unstructured environments.
Given an OGM, this paper addresses the design of
a path planning algorithm to generate a path in a very
short time. Anytime path planners (Ferguson et al.,
2005) have been shown suitable to be used with robots
that have a limited amount of time to perform path
planning. These algorithms compute an initial solu-
tion highly suboptimal very fast and improves it un-
til time runs out. Deterministic anytime approaches,
like the Anytime Repairing A* (ARA*) (Likhachev
et al., 2004), speed up the path generation by inflating
the heuristics to force the exploration of those config-
uration that are closer to the goal according to their
heuristics. During successive iterations the inflation
factor is decreased in order to generate improved so-
lutions. On the other side, sampling-based anytime
algorithms such as Anytime-RRT (ARRT) (Ferguson
and Stentz, 2006), generate a series of RRTs where
each new tree reuses the cost information from the
previous tree to control its growth and thus improve
the quality of the resultant path. At each iteration,
anytime path planners try to improve the solution by
decreasing the heuristics/cost inflation. However, the
generation of a new/better path is not ensured (a path
with the same cost can be obtained).
Topological approaches are another way to tackle
the path planning problem. This kind of solu-
tions work with a graph-based abstraction of the
workspace, in which the environment is represented
by a reduced number of potential states over the afore-
mentioned strategies (Dudek et al., 1991; Fabrizi and
Saffiotti, 2000). Visibility graphs (Latombe, 1991)
and voronoi diagrams (Takahashi and Schilling,
1989) constitute well-known approaches in this re-
gard. Other methods use homotopy classes to provide
a topological description of how paths avoid obsta-
cles. Two paths that share the start point and the end
point belong to the same homotopy class if one can be
deformed into the other without encroaching any ob-
stacle. Some authors compute the shortest homotopic
path of a given input path (Chazelle, 1982; Grigoriev
and Slissenko, 1998; Efrat et al., 2002; Bespamyat-
nikh, 2003). However, in most of robotics applica-
tions the path is not known in advance. (Fujita et al.,
2003; Bhattacharya et al., 2010) generate an initial
path, whose homotopy class is then obtained in order
to prevent the algorithm to generate another path with
the same topology. This methodology achieves the
123
Hernández E., Carreras M. and Ridao P..
A Bug-based Path Planner Guided with Homotopy Classes.
DOI: 10.5220/0004041201230131
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 123-131
ISBN: 978-989-8565-22-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

generation of a path for different homotopy classes by
blocking those previously explored, which make them
suitable for computing the shortest path, but not for
generating a solution with a different homotopy, since
it would require to compute several paths to achieve
the desired solution. To overcome this problem, some
methods (Jenkins, 1991; Schmitzberger et al., 2002)
first generate a set of homotopy classes, allowing to
look directly for a path with a specific topology. How-
ever, they require establishing a set of restriction cri-
teria in order to generate only those homotopy classes
that have an interest for the problem we need to solve.
A solution to this problem has been has been proposed
in (Hern
´
andez et al., 2011a; Hern
´
andez et al., 2011c).
In this paper we propose a bug-based path planner
called Homotopic Bug (HBug), which is guided topo-
logically with homotopy classes. Although bug al-
gorithms were initially conceived to achieve reactive
online navigation for robots with low computational
capabilities in unknown scenarios, it is also possible
to use them to perform deliberative path planning on
a Configuration Space (C-space) (Antich et al., 2009).
The HBug follows the homotopy classes generated
with a method we presented in (Hern
´
andez et al.,
2011a) and improved in (Hern
´
andez et al., 2011c).
Using the topological information, the path planner
does not have to explore the whole space but the
space confined in a homotopy class, speeding up the
path computation. Moreover, homotopy classes allow
the generation of paths that avoid obstacles in differ-
ent manners, which is interesting for surveilling pur-
poses. Unlike anytime approaches, which start the
path search with a highly suboptimal solution, the
HBug starts looking for a path in a homotopy class
that has a high probability of containing the optimal
solution. The method is proved to be complete be-
cause in case the goal is not reachable, no homotopy
classes will exist and, consequently, no paths will be
generated. It is important to note that the homotopy
class of the global optimal path is guaranteed to be
generated by the algorithm. Results and comparison
with other path planners show the efficiency and the
performance of our method, achieving near to opti-
mal solutions with respect to the homotopy class in
unstructured environments with irregular obstacles,
which are the target scenarios of our method.
The paper is structured as follows. Section 2
summarizes the method to generate homotopy classes
from the workspace. Section 3 describes the
topologically-guided path planning algorithm that we
propose. Section 4 reports the results, and section 5
exposes the conclusions and future work.
2 HOMOTOPY CLASSES OF THE
WORKSPACE
Two paths that share the start point and the end point
belong to the same homotopy class if one can be de-
formed into the other without encroaching any obsta-
cle. Therefore, homotopy classes provide topological
information of how paths that belong to a class would
avoid the obstacles. In (Hern
´
andez et al., 2011c)
we presented a method to compute all the homotopy
classes of any 2D workspace, whose steps are sum-
marized in the following sections.
2.1 Reference Frame
The reference frame determines in the metric space
the topological relationships between obstacles and it
is used to name the homotopy classes. To build it, ev-
ery obstacle is represented by a single point b
k
. Then,
a set of lines join each b
k
point and a cental point c
placed in the free space. The lines are partitioned into
segments according the intersections with the obsta-
cles and labeled α
k
s
or β
k
s
depending on the side of
the obstacle they rely on, where k is the obstacle in-
dex and s is the segment index within the line.
The reference frame allows to represent any path
as the sequence of labels of the segments being
crossed in order from the starting to the ending point.
For instance, Figure 1a depicts a reference frame
for a scenario with two obstacles. The path that
traverses it is labeled β
1
1
α
1
0
α
2
0
α
1
0
α
2
0
α
2
0
α
1
0
α
1
−1
.
Notice that this path is topologically equivalent to
β
1
1
α
1
0
α
2
0
α
1
−1
, which is the canonical sequence of
the homotopy class, since is the simplest repre-
sentation of a path without changing its topology
(Hern
´
andez et al., 2011c).
2.2 Topological Graph
The topological graph, whose construction is based
on the reference frame, provides a model to de-
scribe the topological relationships between regions
of the metric space. The reference frame divides the
workspace into several regions. Each region repre-
sents a node of the topological graph. The nodes are
interconnected according to the number of segments
they share in the reference frame. Each edge of the
graph is labeled with the same label of the segment
that crosses in the reference frame.
In the reference frame, a path is defined according
to the segments it crosses whereas in the topological
graph it turns into traversing the graph from the start-
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
124

1
1
−
α
1
2
β
g
0
1
α
1
1
−
α
1
2
β
0
2
α
2
b
0
1
α
0
1
α
0
2
α
0
2
α
c
p
1
l
2
l
1
b
1
1
β
1
2
−
α
s
1
α
2
β
g
3.2
3.1
0
1
α
1
1
−
α
1
2
β
0
2
α
2
b
1.1
4.1 2.1
0
1
α
0
1
α
0
2
α
0
2
α
c
1
b
1
1
β
1
2
−
α
s
1.2
a) Reference frame b) Topological graph
Figure 1: Topological path represented in the reference
frame as p = β
1
1
α
1
0
α
2
0
α
1
0
α
2
0
α
2
0
α
1
0
α
1
−1
and its canoni-
cal sequence (β
1
1
α
1
0
α
2
0
α
1
−1
) in the topological graph.
ing node to the ending node
1
. Figure 1a depicts a path
in the reference frame and Figure 1b its equivalent de-
scription in the topological graph.
2.3 Generation of Homotopy Classes
Once the topological graph is constructed, it is tra-
versed with a modified version of the Breadth-First
Search (BFS) algorithm used in (Hern
´
andez et al.,
2011a; Hern
´
andez et al., 2011c), which incrementally
builds the candidate homotopy classes according to
the edges traversed during the graph search. The al-
gorithm stops when there are no more homotopy class
candidates to explore or the length of the last homo-
topy class candidate is larger than a given threshold.
Notice that those homotopy classes which either self-
intersect or whose canonical sequence is duplicated
are not considered (Hern
´
andez et al., 2011b).
2.4 Lower Bound
Depending on the number of homotopy classes gener-
ated by the BFS algorithm, it is not possible to com-
pute all their correspondent paths in the workspace in
real-time. Therefore, we have modified the funnel al-
gorithm (Chazelle, 1982) to obtain a quantitative mea-
sure for each homotopy class estimating their quality.
This algorithm computes the shortest path within a
channel, which is a polygon formed by the vertexes of
the segments of the reference frame that are traversed
in the topological graph. The modification consists
of accumulating the Euclidean distance between the
points while they are being added to the shortest path.
Hence, the result of the funnel algorithm is a lower
bound of the optimal path in the workspace of the se-
lected homotopy class, which is used to set up a pref-
1
Starting and ending nodes are those regions in the refer-
ence frame where the starting and ending points are located.
g
2
l
2
O
1
O
h
1
l
2
h
2
linem
−
s
1
h
Figure 2: Example of execution of Bug2 algorithm in a sim-
ple scenario.
erence order to compute the homotopy classes path in
the workspace. Figure 3a depicts an example where
the funnel algorithm computes the lower bound for
the homotopy class β
1
1
α
1
0
α
2
0
α
1
−1
. The solid lines
represents the channel and the dashed line is the path
after applying the algorithm. Notice that our vari-
ant of the funnel algorithm takes into account that
some subsegments may self-intersect when creating
the channel (α
1
0
and α
2
0
in Figure 3a).
3 BUG-BASED PATH PLANNING
Once the homotopy classes are computed and sorted
according to their lower bound, a path planning algo-
rithm has to find a path in the workspace that follows a
given homotopy class, which essentially implies turn-
ing a topological path into a metric path. The only
link between the workspace and the topological space
is the reference frame. It allows checking whether
a metric path in the workspace is following a topo-
logical path by following the intersections –in order–
from the initial configuration to the current configura-
tion.
3.1 The Bug2 Algorithm
Our proposal is a path planning algorithm based on
the Bug2 (Lumelsky and Stepanov, 1987). The Bug2
starts by setting up an imaginary line, called m-line,
which connects the start point with the goal point. The
robot starts by following the m-line until the contact
point with an obstacle, which is the first hit point h
1
.
Then, a boundary following behavior surrounds the
obstacle until it reaches a point in the m-line which is
closer to the goal than the previous hit point, that is
the first leave point l
1
. The same process is repeated
until the goal is found. Figure 2 depicts a path gen-
erated by the Bug2 algorithm. Note that the direction
to circumnavigate the obstacles can be fixed at the be-
ginning of the execution or chosen randomly.
ABug-basedPathPlannerGuidedwithHomotopyClasses
125

3.2 Homotopic Bug
As stated before, the path planning algorithm we pro-
pose, which is called Homotopic Bug (HBug), is
based on the Bug2. Essentially, it tries to follow di-
rectly the lower bound path obtained with the mod-
ified funnel algorithm, which ensures that the ho-
motopy class is being accomplished. However, the
segments of the reference frame constrain the region
where the paths can go through, but do not take into
account the shape of the obstacles. For this reason, the
lower bound path may intersect with the obstacles. In
such case, the obstacle boundary is followed in clock-
wise or counterclockwise direction according to the
homotopy class until the lower bound path leaves the
obstacle. This process is repeated for all the inter-
sected obstacles by the lower bound path.
The HBug, detailed in Algorithm 1, receives as
an input parameters the lower bound path P, a can-
didate homotopy class to follow H and the reference
frame F. Notice that the first and the last elements of
P are the start (s) and goal (g) nodes respectively. The
algorithm is a three step process. First, the function
BoundaryNodes checks the intersections of P with
the obstacles in the C-space. Every time that P hits or
leaves an obstacle, a boundary node is created. Each
node contains the contact point c and the obstacle la-
bel k, which is the subindex of the point b
k
that rep-
resents the obstacle in the reference frame. These pa-
rameters are accessible through the functions Q and
Obst respectively. Then, ObstacleNodes computes
the nodes O based on the boundary nodes N previ-
ously computed. Each obstacle node contains the first
boundary node that hits the obstacle n
h
, the last node
that is in its boundary without changing the obstacle
n
l
, and the direction d to surround the obstacle while
following H (line 23). Finally, the function BuildPath
creates the path P
0
in the workspace by joining the
boundary of each obstacle o
i
∈ O from n
h
to n
l
with
the direction d.
The direction d to surround an obstacle is set ac-
cording to the direction of a hit node n
h
towards its
successor n
h+1
2
respect to the point b
k
, that represents
the obstacle of the workspace in the reference frame.
Notice that n
h
and n
h+1
are ensured to belong to the
same obstacle since for any point that hits an obstacle
there has to be another one that releases it. The per-
pendicular dot product between vectors (Q(n
h
) − b
k
)
and (Q(n
h+1
)−b
k
) computes the boundary following
direction (line 15). If the result is less than 0 the di-
rection from n
h
to n
h+1
is counterclockwise; if it is
greater than 0 the direction is clockwise.
2
When the lower bound path intersect with obstacle just
one time, the n
h+1
node is also the n
l
node.
Algorithm 1: Homotopic Bug.
BoundaryNodes(P)
1: N ←
/
0
2: for i ← 1 to |P| − 1, p
i
∈ P do
3: C ← ContourPoints(p
i
, p
i+1
)
4: for all j ← 1 to |C|,c
j
∈ C do
5: k ← Label(c
j
)
6: N ← N ∪ {c
j
,k}
7: end for
8: end for
9: return N
ObstacleNodes(N, H, F)
10: O ←
/
0
11: h ← 1
12: while n
h
∈ N/h < |N| − 1 do
13: n
l
← last n
j
∈ N/ j > h without changing Obst(n
h
)
14: b
k
← point of Obst(n
h
) in F
15: d ← (Q(n
h
) − b
k
)
⊥
· (Q(n
h+1
) − b
k
)
16: if d = 0 then {parallel}
17: d ← (s − b
k
)
⊥
· (point of 1
st
χ
k
∈ H −b
k
)
18: i
k
← index of χ
k
∈ H where n
h+1
relies on
19: if |χ
k
| ∈ H
1..i
k
is even then
20: switch d
21: end if
22: end if
23: O ← O ∪ {n
h
,n
l
,d}
24: h ← l + 1
25: end while
26: return O
BuildPath(O)
27: P
0
←
/
0
28: for i ← 1 to |O|,o
i
∈ O do
29: P
0
← P
0
∪ Boundary(o
i
)
30: end for
31: return P
0
HBug(P,H, F)
32: N ← BoundaryNodes(P)
33: O ← ObstacleNodes(N, H, F)
34: P
0
← BuildPath(O)
The result of the perpendicular dot product can
be 0 if the vectors (Q(n
h
) − b
k
) and (Q(n
h+1
) − b
k
)
are parallel, which means that n
h
, n
h+1
and b
k
be-
long to the same l
k
in the reference frame (line 16).
In such case, d is obtained according two conditions:
the initial direction selected to cross l
k
from the start
point, and the number of times that l
k
is crossed until
the α
k
or β
k
–denoted by χ
k
– of the homotopy class,
where n
h+1
relies on, is reached. The initial direction
is obtained with the dot product form the start s to
the first χ
k
with the same subindex than l
k
3
(line 17).
The number of times that l
k
is crossed depends on the
number of χ
k
found in the homotopy class from the
beginning to the index i
k
, which indicates the position
3
Notice that the start point cannot be in a line l
k
of the
reference frame since the perpendicular dot product would
be also 0.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
126
1
1
−
α
1
2
β
g
2
b
0
1
α
α
2
1
b
1
β
0
2
α
α
1
1
β
1
2
−
α
s
1
1
−
α
1
2
β
g
}2,{:
44
cn
0
1
α
2
b
ccw
}2,{:
33
cn
1
b
0
2
α
}
1
,
{
:
c
n
}1,{:
22
cn
1
b
1
1
β
1
2
−
α
s
cw
}
1
,
{
:
11
c
n
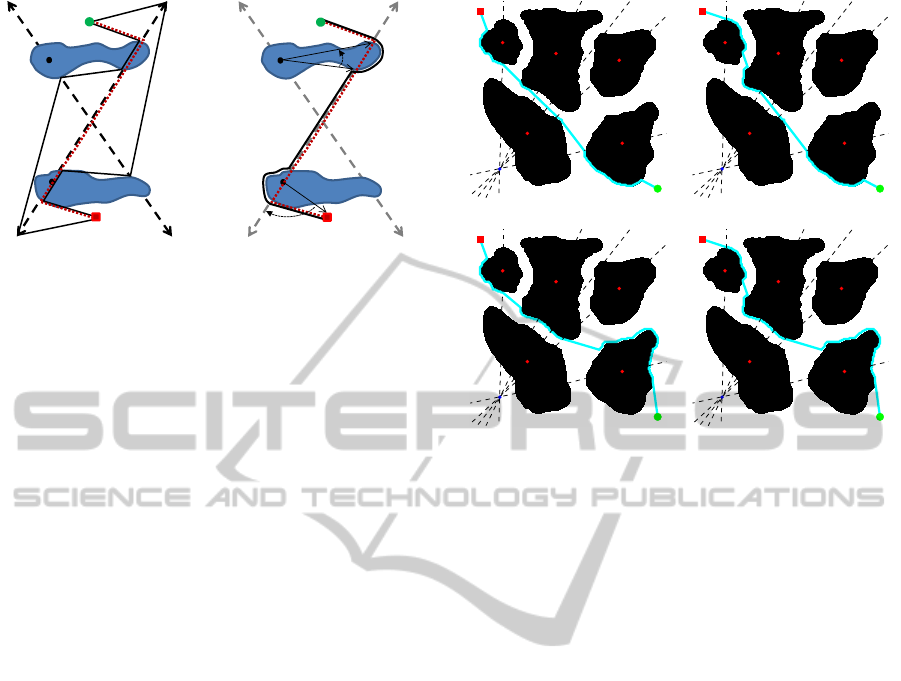
a) Channel and lower bound path b) Path computed with the HBug
Figure 3: Generation of the lower bound path and the HBug
path for the homotopy class β
1
1
α
1
0
α
2
0
α
1
−1
.
of the χ
k
that contains n
h+1
(line 19).
Figure 3 depicts an example scenario where the
HBug is applied. The homotopy class to follow is
β
1
1
α
1
0
α
2
0
α
1
−1
. The dashed line represents its lower
bound path, which intersects with the first obstacle
generating two boundary nodes n
1
and n
2
, both of
them located on the line l
1
of the reference frame.
The point that represents the obstacle is b
1
, also on
l
1
, which makes perpendicular dot product between
(Q(n
1
) − b
1
) and (Q(n
2
) − b
1
) unable to set the di-
rection (d = 0). Therefore, using the start point s
and a point of the edge β
1
1
, the initial direction is set
clockwise (cw). The last edge involved in this situ-
ation is α
1
0
, which is located in the second position
in the homotopy class. The number of edges with
subindex 1 till this position is 2. Thus, the direction
is not changed. Then, the lower bound path intersects
with the second obstacle in n
3
and n
4
. Using the base
point b
2
, the perpendicular dot product sets the direc-
tion as counterclockwise (ccw). Finally, the path is
composed from s to g with the boundaries of the ob-
stacle 1 (from n
1
to n
2
) and the obstacle 2 (from n
3
to
n
4
) joint by straight lines.
4 RESULTS
The feasibility the topological path search with the
HBug has been tested in different bitmap scenarios
which have been used as C-spaces, where the robot is
represented as a single point. To identify the obsta-
cles of the scenarios we have adapted a Component-
Labeling (CL) algorithm that efficiently labels con-
nected cells and their contours in greyscale images
at the same time (Chang et al., 2004). The contours
of the obstacles provided by this algorithm are used
by the HBug to avoid recomputing them at each new
path search. For the construction of the reference
frame, the c point has been set at a fixed position in
b
1
b
2
b
3
b
4
b
5
α
1
0
α
1
1
β
1
2
α
2
0
α
2
1
β
2
2
α
3
0
α
3
1
α
3
2
β
3
3
α
4
0
β
4
1
β
4
2
β
4
3
α
5
0
α
5
1
β
5
2
c
s
g
b
1
b
2
b
3
b
4
b
5
α
1
0
α
1
1
β
1
2
α
2
0
α
2
1
β
2
2
α
3
0
α
3
1
α
3
2
β
3
3
α
4
0
β
4
1
β
4
2
β
4
3
α
5
0
α
5
1
β
5
2
c
s
g
2-α
2
1
α
1
1
β
4
1
α
3
1
α
5
1
8-β
2
2
α
1
1
β
4
1
α
3
1
α
5
1
b
1
b
2
b
3
b
4
b
5
α
1
0
α
1
1
β
1
2
α
2
0
α
2
1
β
2
2
α
3
0
α
3
1
α
3
2
β
3
3
α
4
0
β
4
1
β
4
2
β
4
3
α
5
0
α
5
1
β
5
2
c
s
g
b
1
b
2
b
3
b
4
b
5
α
1
0
α
1
1
β
1
2
α
2
0
α
2
1
β
2
2
α
3
0
α
3
1
α
3
2
β
3
3
α
4
0
β
4
1
β
4
2
β
4
3
α
5
0
α
5
1
β
5
2
c
s
g
3-α
2
1
α
1
1
β
4
1
α
3
1
β
5
2
9-β
2
2
α
1
1
β
4
1
α
3
1
β
5
2
Figure 4: Paths for the four homotopy classes with the
smaller lower bound in Table 1.
order to ensure the same topological graph construc-
tion –and homotopy classes generation– through dif-
ferent executions. The homotopy classes have been
set at a maximum of 20 characters length. In order
to show all the possible results, no time restrictions
have been taken into consideration. The computations
have been carried out with a laptop equipped with an
Intelr Core
TM
Duo@1.83GHz processor and 2GB of
RAM.
4.1 Cluttered Environment
Our method has been applied in a cluttered environ-
ment using a 200x200 pixels bitmap. Figure 4 de-
picts the scenario with the paths of the best homo-
topy classes, according to their lower bound. The
construction of the reference frame, the topological
graph and the generation of the homotopy classes with
their lower bound computation took 7.9ms. Table 1
shows the homotopy classes sorted by their lower
bound with the path cost and the accumulated com-
putation time, which takes into account the homotopy
classes computation and the path generation. The
lower bound and the path cost have been normalized
with the cost of the optimal path computed with the
A* algorithm. It can be appreciated that using the
HBug the computation time for the paths of the 13 ho-
motopy classes is almost negligible (0.374ms) com-
pared with the 7.9ms that takes the rest of the process.
When operating under time restrictions, it is pos-
sible to stop the path search when the lower bound
ABug-basedPathPlannerGuidedwithHomotopyClasses
127
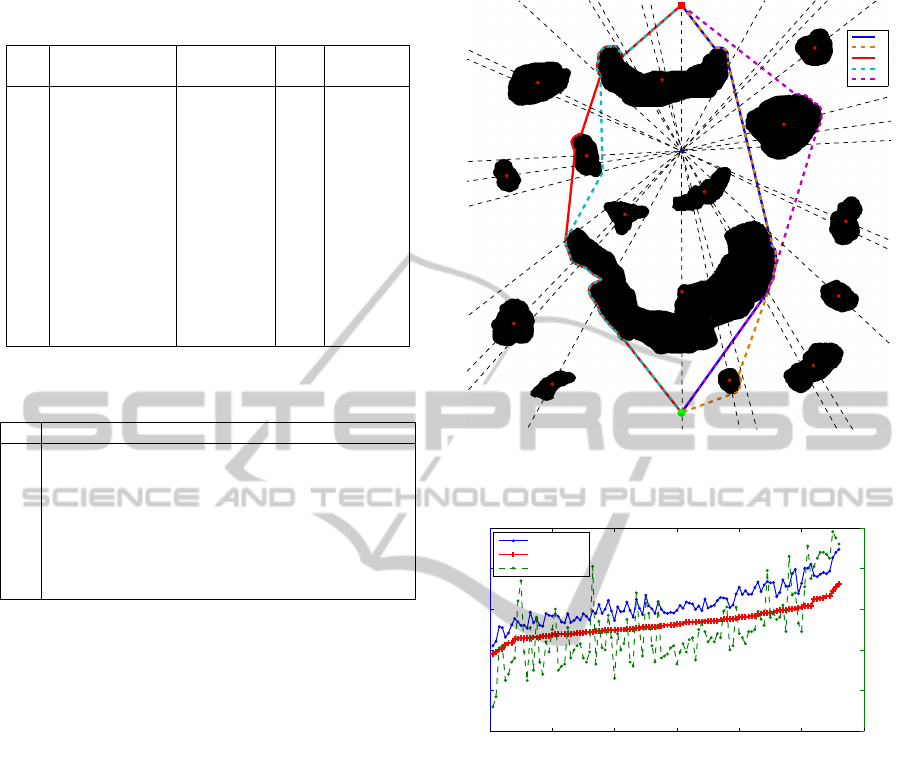
Table 1: Homotopy classes of Figure 4 environment sorted
by their lower bound.
Idx Homotopy class Lower bound Cost Cumulated
time (ms)
2 α
2
1
α
1
1
β
4
1
α
3
1
α
5
1
0.93 1.16 7.927
8 β
2
2
α
1
1
β
4
1
α
3
1
α
5
1
0.94 1.20 7.950
3 α
2
1
α
1
1
β
4
1
α
3
1
β
5
2
0.99 1.43 7.981
9 β
2
2
α
1
1
β
4
1
α
3
1
β
5
2
1.00 1.45 8.007
1 α
5
0
α
3
0
α
4
0
α
1
0
α
2
0
1.04 1.48 8.035
11 β
2
2
β
1
2
β
4
2
α
3
2
β
5
2
1.08 1.53 8.063
10 β
2
2
β
1
2
β
4
2
α
3
2
α
5
1
1.13 1.51 8.084
13 β
2
2
β
1
2
β
4
3
β
3
3
β
5
2
1.18 1.31 8.106
5 α
2
1
β
1
2
β
4
2
α
3
2
β
5
2
1.26 2.02 8.142
4 α
2
1
β
1
2
β
4
2
α
3
2
α
5
1
1.32 1.99 8.174
7 α
2
1
β
1
2
β
4
3
β
3
3
β
5
2
1.36 1.80 8.205
12 β
2
2
β
1
2
β
4
3
β
3
3
α
5
1
1.40 1.77 8.236
6 α
2
1
β
1
2
β
4
3
β
3
3
α
5
1
1.58 2.26 8.274
Table 2: The five homotopy classes of the large environment
with the smaller lower bound and their generation index.
Idx Homotopy class
25 α
15
−1
α
9
0
α
12
0
α
1
0
α
4
0
α
6
0
α
5
0
α
8
1
α
3
−1
α
11
2
α
13
2
β
7
2
α
2
−2
α
14
2
β
10
2
26 α
15
−1
α
9
0
α
12
0
α
1
0
α
4
0
α
6
0
α
5
0
α
8
1
α
3
−1
α
11
2
α
13
2
β
7
2
α
2
−2
β
14
3
β
10
2
5 α
10
−1
α
14
−1
β
2
1
α
7
−1
α
13
−1
α
11
−1
α
3
0
α
8
0
β
5
1
α
6
1
α
4
−1
α
1
−2
α
12
2
...
...β
9
2
α
15
2
1 α
10
−1
α
14
−1
β
2
1
α
7
−1
α
13
−1
α
11
−1
α
3
0
α
8
0
α
5
0
α
6
0
α
4
0
α
1
−2
α
12
2
...
...β
9
2
α
15
2
41 α
15
−1
α
9
0
α
12
0
α
1
0
β
4
1
α
6
−1
α
5
−1
α
8
1
α
3
−1
α
11
2
α
13
2
β
7
2
α
2
−2
...
...α
14
2
β
10
2
of the next homotopy class –whose path is going to
be computed– is higher than the minimum cost of the
paths already computed. In such case, it is ensured
that the best path with the HBug has been already
computed because it is not possible to obtain a path
with a lower cost than the lower bound. For instance,
in Table 1 the HBug would stop before computing
path for homotopy class with index 13 since its lower
bound (1.18) is higher than the path length obtained
with index 2 class (1.16).
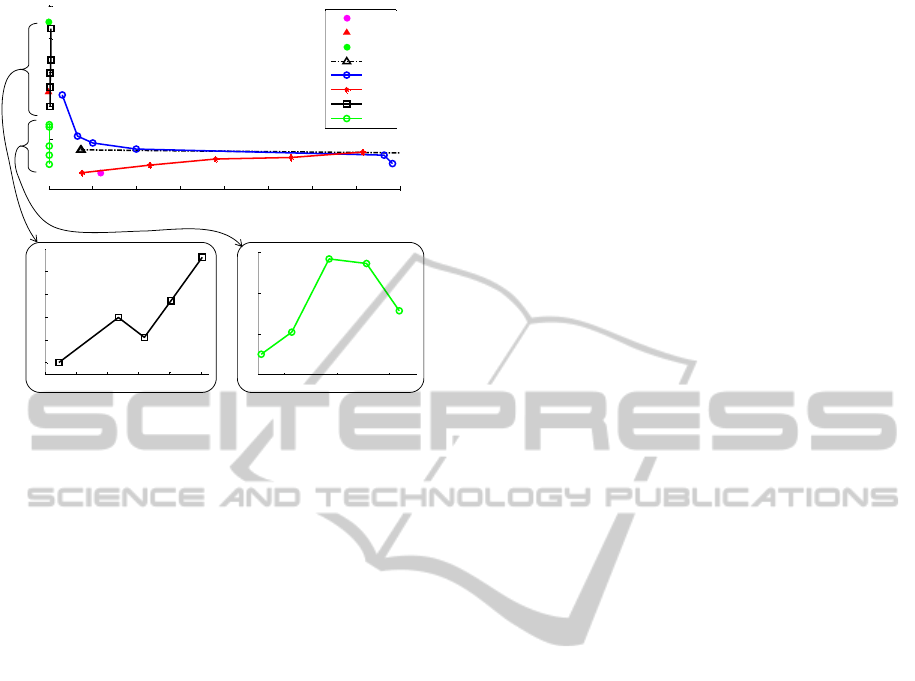
4.2 Scalability
The scalability of the method has been tested in a
bitmap of 1000x1000 pixels with 15 irregular obsta-
cles (Figure 5). The construction of the reference
frame, the topological graph and the generation of
112 homotopy classes with their lower bound compu-
tation took 0.304s. The HBug has been used to com-
pute the path for all homotopy classes of the scenario.
The homotopy classes with the smaller lower bound,
shown in Table 2, and their paths computed with the
HBug are depicted in Figure 5. Figure 6 shows the
cost and computation time for each homotopy class
path computed with the HBug. The homotopy classes
have been sorted according to their lower bound. The
path cost and the lower bound have been normalized
b
1
b
2
b
3
b
4
b
5
b
6
b
7
b
8
b
9
b
10
b
11
b
12
b
13
b
14
b
15
α
1
0
α
1
−1
α
1
−2
β
1
1
α
2
0
β
2
1
α
2
−1
α
2
−2
α
3
0
β
3
1
α
3
−1
α
3
−2
α
4
0
α
4
−1
β
4
1
α
5
0
β
5
1
β
5
2
α
5
−1
α
6
0
α
6
1
β
6
2
α
6
−1
α
7
0
α
7
−1
β
7
1
β
7
2
β
7
3
α
8
0
α
8
−1
α
8
1
β
8
2
α
9
0
β
9
1
β
9
2
β
9
3
α
10
0
α
10
−1
α
10
1
β
10
2
α
11
0
α
11
−1
α
11
1
α
11
2
β
11
3
α
12
0
α
12
1
α
12
2
β
12
3
α
13
0
α
13
−1
α
13
1
α
13
2
β
13
3
α
14
0
α
14
−1
α
14
1
α
14
2
β
14
3
α
15
0
α
15
1
α
15
2
β
15
3
α
15
−1
c
s
g
25
26
5
1
41
Figure 5: Paths of the five homotopy classes with the
smaller lower bound computed with the HBug. The class
associated to the index can be found in Table 2.
0 20 40 60 80 100 120
0
0.5
1
1.5
2
2.5
Nº of homotopy class
Lower bound & Cost
0 20 40 60 80 100 120
1
1.2
1.4
1.6
1.8
2
x 10
−4
Time (s)
Cost
Lower bound
Time
Figure 6: Normalized cost, normalized lower bound and
computation time for paths generated with the HBug for
each homotopy class.
with respect to the A* path cost. If time restrictions
were applied, the HBug would compute only till the
fourth path.
The fastest path was generated in 1.12x10
−4
s. It
corresponds to the first class (index 25) with a path
cost only 1.05 times the optimal solution. The homo-
topy class 110 (index 102) was the one that took more
time to be computed (1.98x10
−4
s) with a cost 2.24
times the global optimal solution. The mean com-
putation per path was only (1.50x10
−4
s). In this en-
vironment, the paths for the whole set of homotopy
classes were computed in 16.8ms, which is almost
negligible when compared with the 304ms spent in the
generation of the reference frame, topological graph
and the generation of the homotopy classes with their
lower bound.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
128
1.8
2
A*
RRT
1.4
1.6
1.8
Cost
RRT
Bug2
ARA*
ARRT
HA*
HRRT
1
1.2
1.4
Cost
HRRT
HBug
0 10 20 30 40 50 60 70 80
1
Time (s)
1.2
1.3
1.6
1.7
1.8
0.3042
0.3044
0.3046
1
1.1
0.35
0.4
0.45
0.5
0.55
0.6
1.4
1.5
1.6
0.3042
0.3044
0.3046
0.35
0.4
0.45
0.5
0.55
0.6
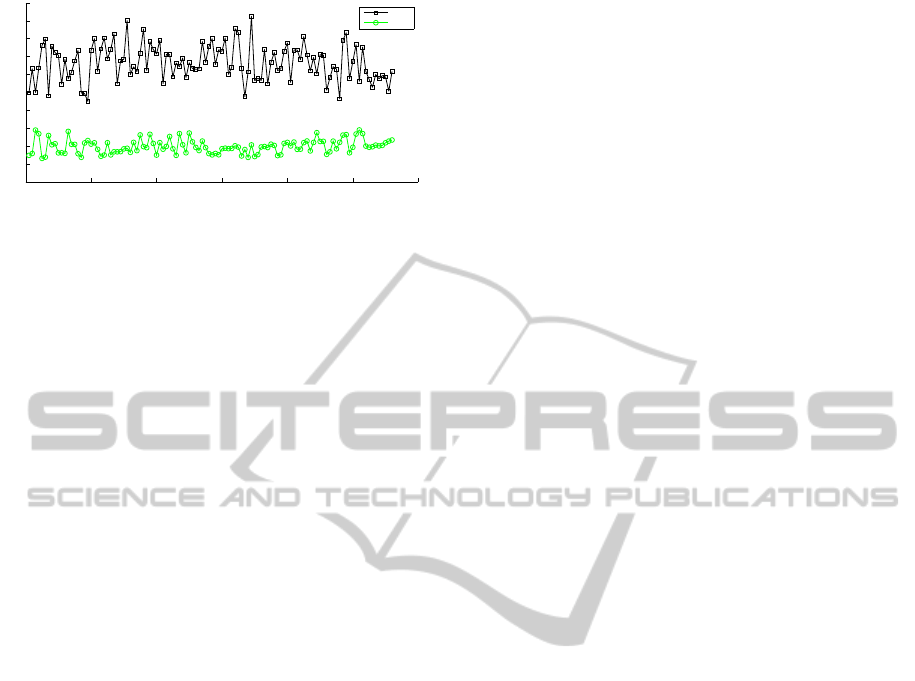
Figure 7: Comparison of the HA*, HRRT and HBug paths
of the five homotopy classes with the smaller lower bound
vs A*, RRT, ARA*, ARRT and Bug2 algorithms.
4.3 Path Planners Comparison
The HBug has been compared against the A*, the
RRT, their respective anytime versions (ARA* and
ARRT) and the Bug2 algorithm. The comparison
also includes the results obtained with the Homotopic
A* (HA*) (Hern
´
andez et al., 2011b) and the Homo-
topic RRT (HRRT) (Hern
´
andez et al., 2011a), two
path planners that constrain the path search according
to the homotopy classes previously generated. The
A*, the RRT and the Bug2 algorithms are designed
to compute only one path towards the goal; ARA*
and ARRT compute several paths but without tak-
ing into account their homotopy. Because of that,
the comparison with these well-known path planners
are against the five homotopy classes with the smaller
lower bound (see Table 2). Figure 7 depicts the com-
parison. In order to ensure the stabilization of the re-
sults of the probabilistic path planners, the data ob-
tained with the RRT and the ARRT are the average of
100 executions. Notice that all the time values of the
HA*, HRRT and HBug include the computation time
of the reference frame and topological graph con-
struction, and the generation of the homotopy classes
with their lower bound.
The A* returned the optimal path in 11.90s. The
ARA* generated the first solution in 7.40s and found
the optimal solution after 301s. The RRT algorithm
took 0.012s to compute a path with a cost 1.48 times
the global optimal solution. The ARRT took 3.13s
to obtain the first solution and 78.30s to compute all
of them, ensuring that any new generated solution is
closer to the optimal one. The Bug2 algorithm com-
puted the path in 0.044s with a cost 1.90 times the
optimal solution. In order to obtain the best possible
path with this algorithm, we have chosen manually
the directions to surround the obstacles: the m-line,
which connects the start with the goal, intersects with
the obstacles labeled b
1
, b
7
and b
10
; the directions are
clockwise for b
1
, counter-clockwise for b
7
and clock-
wise for b
10
.
The HA* computed the optimal path (index 25) in
7.79s and obtained the path for the five selected ho-
motopy classes in 71.61s. The HRRT, the best solu-
tion (index 25) was computed in 0.373s with a cost
1.40 times the optimal one, and obtained the path
for the five homotopy classes with the smaller lower
bound in 0.603s. Using the HBug, our path plan-
ning method computed the best solution (index 25) in
0.304s with a cost 1.05 times the optimal one, and ob-
tained the path for the whole set of homotopy classes
in 0.321s. The computation of the paths with the
HBug for each homotopy class offers a very good per-
formance. Only the RRT and Bug2 had lower com-
putation times at expenses of finding higher cost so-
lutions. Notice that most of the time was spent in
the computation of the reference frame, the topologi-
cal graph and the generation of the homotopy classes
with their lower bound. The HBug shows a very good
performance because part of its solution is implicitly
generated on the lower bound computation. When
the lower bound path intersects with an obstacle of
the scenario, its boundary is followed in clockwise
or counterclockwise direction according to the homo-
topy class until the lower bound path leaves the obsta-
cle. Notice that the whole boundary of each obstacle
is already computed by the CL algorithm.
The HA* computes the shortest path for each ho-
motopy class, which is the optimal solution according
to the topological constraints. Because of that, Fig-
ure 8 depicts a comparison of the solutions generated
with the HRRT and the HBug against the HA* cost
for each specific homotopy class. The HRRT gener-
ates solutions between 1.35 (class 15, index 73) and
1.82 (class 83, index 61), with a mean of 1.57 times
with respect the optimal path cost for the specific ho-
motopy class generated with the HA*. Finally, the
HBug generates solutions between 1.03 (class 5, in-
dex 41) and 1.19 (class 100, index 101), with a mean
of 1.1 times with respect the optimal path cost com-
puted with the HA*.
5 CONCLUSIONS
This paper proposes the HBug path planning algo-
rithm to compute efficiently paths that accomplish ho-
ABug-basedPathPlannerGuidedwithHomotopyClasses
129
0 20 40 60 80 100 120
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
Nº of homotopy class
Cost
HRRT
HBug
Figure 8: HRRT and HBug paths cost with respect to the
HA* cost for each homotopy class.
motopy classes in any 2D workspace. Given a map
with obstacles, we use a method we developed to gen-
erate systematically the homotopy classes of the en-
vironment. After sorting them according to a lower
bound, the HBug algorithm generates paths in the
C-space following the homotopy classes previously
found. The path planner offers very good perfor-
mance since the path search for a homotopy class
is guided by its lower bound, making the path plan-
ning computation time almost negligible when com-
pared with the time used to generate the homotopy
classes. Results obtained with the HBug, have shown
up that it is a homotopic path planner suitable for
robots with very limited computational capabilities or
applications in which the time to perform path plan-
ning is highly constrained.
Future work will consists in applying our method
into one of the vehicles of our lab. The HBug will be
improved by taking into account the robot’s kinody-
namic constraints during the path generation. These
paths will be used to guide the robot autonomously.
ACKNOWLEDGEMENTS
The authors of this paper gratefully acknowledge the
support from Spanish government under the grant
DPI2011-27977-C03-02 and the TRIDENT EU FP7-
Project under the grant agreement No: ICT-248497.
REFERENCES
Antich, J., Ortiz, A., and Minguez, J. (2009). A bug-
inspired algorithm for efficient anytime path planning.
In IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS), pages 5407 –5413.
Bespamyatnikh, S. (2003). Computing homotopic shortest
paths in the plane. Journal of Algorithms, 49:284–
303.
Bhattacharya, S., Kumar, V., and Likhachev., M. (2010).
Search-based path planning with homotopy class con-
straints. In Proceedings of the National Conference on
Artificial Intelligence (AAAI), volume 2, pages 1230–
1237, Atlanta, Georgia, USA.
Chang, F., jen Chen, C., and Lu, C.-J. (2004). A linear-time
component-labeling algorithm using contour tracing
technique. Computer Vision and Image Understand-
ing, 93:206–220.
Chazelle, B. (1982). A theorem on polygon cutting with ap-
plications. In 23rd Annual Symposium on Foundations
of Computer Science (SFCS), pages 339 –349.
Dudek, G., Jenkin, M., Milios, E., and Wilkes, D. (1991).
Robotic exploration as graph construction. IEEE
Transactions on Robotics and Automation, 7(6):859–
865.
Efrat, A., Kobourov, S., and Lubiw, A. (2002). Comput-
ing homotopic shortest paths efficiently. In M
¨
ohring,
R. and Raman, R., editors, Algorithms – ESA 2002,
volume 2461 of Lecture Notes in Computer Science,
pages 277–288. Springer Berlin / Heidelberg.
Fabrizi, E. and Saffiotti, A. (2000). Extracting topology-
based maps from gridmaps. In IEEE International
Conference on Robotics and Automation (ICRA),
pages 2972–2978.
Ferguson, D., Likhachev, M., and Stentz, A. (2005). A
guide to heuristic-based path planning. In Proceed-
ings of the International Workshop on Planning under
Uncertainty for Autonomous Systems, International
Conference on Automated Planning and Scheduling
(ICAPS).
Ferguson, D. and Stentz, A. (2006). Anytime RRTs. In Pro-
ceedings of the IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS), pages 5369 –
5375.
Fujita, Y., Nakamura, Y., and Shiller, Z. (2003). Dual dijk-
stra search for paths with different topologies. In IEEE
International Conference on Robotics and Automation
(ICRA), volume 3, pages 3359–3364.
Grigoriev, D. and Slissenko, A. (1998). Polytime algorithm
for the shortest path in a homotopy class amidst semi-
algebraic obstacles in the plane. In Proceedings of the
International Symposium on Symbolic and Algebraic
Computation (ISSAC), pages 17–24, New York, NY,
USA. ACM.
Hern
´
andez, E., Carreras, M., Antich, J., Ridao, P., and
A.Ortiz (2011a). A topologically guided path planner
for an AUV using homotopy classes. In Proceedings
of the IEEE International Conference on Robotics
and Automation (ICRA), pages 2337–2343, Shanghai,
China.
Hern
´
andez, E., Carreras, M., Antich, J., Ridao, P., and Or-
tiz, A. (2011b). A search-based path planning al-
gorithm with topological constraints. Application to
an AUV. In Proceedings of the 18th IFAC World
Congress, Milan, Italy.
Hern
´
andez, E., Carreras, M., and Ridao, P. (2011c). A path
planning algorithm for an AUV guided with homo-
topy classes. In Proceedings of the 21st International
Conference on Automated Planning and Scheduling
(ICAPS), Freiburg, Germany.
Jenkins, K. D. (1991). The shortest path problem in the
plane with obstacles: A graph modeling approach
to producing finite search lists of homotopy classes.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
130

Master’s thesis, Naval Postgraduate School, Mon-
terey, California.
Latombe, J. (1991). Robot Motion Planning. Kluwer Aca-
demic Publishers, Boston, MA.
Likhachev, M., Gordon, G., and Thrun, S. (2004). ARA*:
Anytime A* with provable bounds on sub-optimality.
In Proceedings of the Advances in Neural Inforamtion
Processing Systems 16 (NIPS). MIT Press.
Lumelsky, V. and Stepanov, A. (1987). Path-planning
strategies for a point mobile automaton moving amidst
unknown obstacles of arbitrary shape. Algorithmica,
2:403–430.
Schmitzberger, E., Bouchet, J., Dufaut, M., Wolf, D., and
Husson, R. (2002). Capture of homotopy classes with
probabilistic road map. In IEEE/RSJ International
Conference on Intelligent Robots and Systems (IROS),
volume 3, pages 2317–2322.
Takahashi, O. and Schilling, R. (1989). Motion planning
in a plane using generalized voronoi diagrams. IEEE
Transactions on Robotics and Automation, 5(2):143 –
150.
ABug-basedPathPlannerGuidedwithHomotopyClasses
131
