Spacecrafts' Control Systems Effective Variants Choice

with Self-Configuring Genetic Algorithm

Eugene Semenkin and Maria Semenkina

Institute of Computer Sciences and Telecommunication, Siberian State Aerospace University,

Krasnoyarskiy Rabochiy Ave., 31, 660014, Krasnoyarsk, Russia

Keywords: Spacecraft Control System, Control Contours Models, Markov Chains, Effective Variant Choice,

Optimization, Self-configuring Genetic Algorithm.

Abstract: The work of the spacecraft control system is modeled with Markov chains. Small and large models for the

technological and command-programming control contours are developed. The way of the calculation of the

control contour effectiveness indicators is described. Special self-configuring genetic algorithm that requires

no settings determination and parameter tuning is proposed for choosing effective variants of spacecraft

control system. The high performance of the suggested algorithm is demonstrated through experiments with

test problems and then is validated by the solving hard optimization problems.

1 INTRODUCTION

Current efforts by the developers of spacecraft are

concentrated upon increasing the usage effectiveness

of existing spacecraft systems and improving the

development and design process for new ones. One

of the ways to achieve these aims is a rational choice

of the effective variants of the developing systems.

This requires the application of adequate models,

effective algorithmic tools and powerful computers.

This application will allow multivariant analysis of

the developing systems that is currently not so easy

due to their complexity.

One of the most difficult and underdeveloped

problems is that of the synthesis of a spacecraft's

control systems. These are currently solved with

more empirical methods rather than formalized

mathematical tools. Usually, the spacecraft control

system design is a sophisticated process involving

the cooperation of numerous experts and

departments each having their own objectives and

constraints. Nevertheless, it is possible to

mathematically model some subproblems and to

obtain some qualitative results of computations and

tendencies that could provide interesting information

for experts. The usual position of system analyst in

such a situation is as mediator for high level decision

making, dealing with informal problems for which it

is impossible to develop a mathematical model, and

lower level computations for which strong

mathematical models exist but the results of them do

not always match. If, in this intermediate position

when mathematical models are strong enough but

very complicated for analysis, we intend to

implement a decision support system for the choice

of effective variants then we have to realize that the

optimization problems arise here are intractable for

the majority of known algorithms.

We suggest modeling the functioning process of

a spacecraft's control subsystems with Markov

chains. We explain the modeling with small models

and then give illustration of large models that are

closer to real system. The problem of choosing an

effective variant for a spacecraft's control system is

formulated as a multi-scale optimization problem

with algorithmically given functions. In this paper,

we use self-configuring genetic algorithm to solve

the optimization problem.

The rest of the paper is organized in the following

way. Section 2 briefly describes the modeled system.

In Sections 3 and 4 we describe small size models for

two control contours. Section 5 illustrates briefly the

view of large models. In Section 6 we describe the

proposed optimization algorithm and in Section 7 we

evaluate its performance on the test problems. In

Section 8, the results of the algorithm performance

evaluation on spacecraft control system optimization

problems is given, and in the Conclusion section the

article content is summarized and future research

directions are discussed.

Semenkin E. and Semenkina M..

Spacecrafts’ Control Systems Effective Variants Choice with Self-conﬁguring Genetic Algorithm .

DOI: 10.5220/0004042200840093

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 84-93

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 PROBLEM DESCRIPTION

The system for monitoring and control of an orbital

group of telecommunication satellites is an

automated, distributed, information-controlling

system that includes in its composition on-board

control complexes (BCC) of spacecrafts; telemetry,

command and ranging (TSR) stations; data

telecommunication subsystems; and a mission

control center (MCC). The last three subsystems are

united in the ground-based control complex (GCC).

GCC interacts with BCC(s) through a distributed

system of TCR stations and data telecommunication

systems that include communication nodes in each

TCR, channels and MCC's associated

communication equipment. BCC is the controlling

subsystem of the spacecraft that ensures real time

checking and controlling of on-board systems

including pay-load equipment (PLE) as well as

fulfilling program-temporal control. Additionally,

BCC ensures the interactivity with ground-based

tools of control. The control functions fulfilled by

subsystems of the automated control system are

considered to form subsets called "control contours"

that contain essentially different control tasks.

Usually, one can consider the technological control

contour, command-programming contour, purpose

contour, etc.

Each contour has its own indexes of control

quality that cannot be expressed as a function of

others. This results in many challenges when

attempting to choose an effective control system

variant to ensure high control quality with respect to

all of the control contours. A multicriterial

optimization problem statement is not the only

problem. For most of the control contours, criterion

cannot be given in the form of an analytical function

of its variables but exists in an algorithmic form

which requires a computation or simulation model to

be run for criterion evaluation at any point.

In order to have the possibility of choosing an

effective variant of such a control system, we have

to model the work of all control contours and then

combine the results in one optimization problem

with many models, criteria, constraints and

algorithmically given functions of mixed variables.

We suggest using evolutionary algorithms (EAs) to

solve such optimization problems as these

algorithms are known as good optimizers having no

difficulties with the described problem properties

such as mixed variables and algorithmically given

functions. To deal successfully with many criteria

and constraints we just have to incorporate

techniques, well known in the EA community.

However, there is one significant obstacle in the use

of EAs for complicated real world problems. The

performance of EAs is essentially determined by

their settings and parameters which require time and

computationally consuming efforts to find the most

appropriate ones.

To support the choice of effective variants of

spacecrafts' control systems, we have to develop the

necessary models and resolve the problem of EAs

settings.

3 TECHNOLOGICAL CONTROL

CONTOUR MODELING

The main task of the technological control contour is

to provide workability of the spacecraft for the

fulfillment of its purposes, i.e., the detecting and

locating of possible failures and malfunctions of the

control system and pay-load and restoring their lost

workability by the activation of corresponding

software and hardware tools. The basic index of the

quality for this contour is the so called readiness

coefficient, i.e., a probability to be ready for work

(hasn’t malfunctioned) at each point in time.

We consider simplified control system to

describe our modeling approach. Let the system

consist of three subsystems: on-board pay-load

equipment, on-board control complex and ground-

based control complex. Let us assume that GCC

subsystems are absolutely reliable but PLE and BCC

can fail. If PLE failed, BCC can restore it using its

own software tools with the probability p

or,

otherwise, re-directs restoring process (with the

probability 1-p

) into GCC that finishes restoring

with the probability equal to 1. In the case of a BCC

malfunction, GCC restores it with the probability

equal to one.

We can use a Markov chain approach to model a

spacecraft’s’ control system operation because of its

internal features such as high reliability and work

stability, e.g., two simultaneous failures are almost

impossible, there is no aftereffect if malfunction

restoring is finished, etc. That is why we will

suppose that all stochastic flows in the system are

Poisson ones with corresponding intensities: 

is an

intensity of PLE malfunctions, 

is an intensity of

BCC malfunctions, 

is an intensity of PLE

restoring with BCC, 

is an intensity of PLE

restoring with GCC, 

is an intensity of BCC

restoring with GCC.

In the described situation, there are five possible

states of the system:

Spacecrafts' Control Systems Effective Variants Choice with Self-configuring Genetic Algorithm

1. All subsystems are workable.

2. PLE malfunction, BCC is restoring PLE, GCC is

free.

3. BCC malfunction, GCC is restoring BCC, PLE is

workable.

4. PLE malfunction, BCC is workable and free,

GCC is recovering PLE.

5. PLE malfunction, BCC malfunction, GCC is

recovering PLE, and BCC is waiting for

recovering.

States graph can be drawn as is shown in Figure 1.

Figure 1: States graph of Markov chain for the simplified

model of a technological control contour.

Corresponding Kolmogorov's equation system is:

·(

+

) - 

·p

·P

- 

·P

- 

·P

= 0,

·(

+

) - 

·P

= 0,

·(

+

) - 

·P

- 

·P

= 0,

·(

+

) - (1-p

)·

·P

= 0,

·

- 

·P

- 

·P

- 

·P

= 0,

+ P

= 1.

The last equation is needed for normalization and

should replace any of previous ones.

Given final probabilities that the system remains

in the corresponding state, as the solution of this

equation system, the control quality indicators, i.e.,

readiness coefficients, can be calculated in following

way:

1. Spacecraft readiness coefficient k

= P

2. PLE readiness coefficient k

PLE

= P

+ P

3. BCC readiness coefficient k

BCC

= P

+ P

To have the effective variant of the spacecraft

control system we have to maximize the readiness

coefficients subject to constraints on the on-board

computer memory and computational efforts needed

for the technological contour functions realization.

Optimization variables are stochastic flow intensities



, 

, 

, as well as p

, i.e., the distribution

of contour functions between BCC and GCC. If they

are characteristics of existing variants of software-

hardware equipment, we have the problem of

effective variant choice, i.e., a discrete optimization

problem. In case of a system preliminary design,

some of the intensities can be real numbers and we

will have to implement corresponding software and

hardware to ensure an optimal solution. Recall that

obtained optimization problem has algorithmically

given objective functions so before the function

value calculation we must solve the equations

system.

4 COMMAND-PROGRAMMING

CONTROL CONTOUR

MODELING

The main task of this contour is the maintenance of

the tasks of creating of the command-programming

information (CPI), transmitting it to BCC and

executing it and control action as well as the

realization of the temporal program (TP) regime of

control.

We can use Markov chains for modeling this

contour for the same reasons. If we suppose that

BCC can fail and GCC is absolutely reliable, then

we can introduce the following notations: 

is the

intensity of BCC failures, 

is the intensity of

temporal program computation, 

is the intensity

CPI loading into BCC, 

is the intensity of temporal

program execution, 

is the intensity of BCC being

restored after its failure. The graph of the states for

command-programming contour can be drawn as in

Figure 2.

Figure 2: States graph of Markov chain for simplified

model of command-programming control contour.

There are also five possible states for this contour:

1. BCC fulfills TP, GCC is free.

2. BCC is free, GCC computes TP.

3. BCC is free; GCC computes CPI and loads TP.

4. BCC is restored with GCC which is waiting for

continuation of TP computation.

ICINCO 2012 - 9th International Conference on Informatics in Control, Automation and Robotics

5. BCC is restored with GCC which is waiting for

continuation of CPI computation.

BCC, restored after any failure in state 1, cannot

continue its work and has to wait for a new TP

computed with GCC. If BCC has failed in state 2 or

state 3 then GCC can continue its computation only

after BCC restoring completion.

If we assume for simplicity that all flows in the

system are Poisson ones, the system of

Kolmogorov's equations can be written as follows.

·(

+

) - 

·P

= 0,

·(

+

) - 

·P

- 

·P

= 0,

·(

+

) - 

·P

- 

·P

= 0,

·

- 

·P

- 

·P

= 0,

·

- 

·P

= 0,

+ P

= 1.

After solving the Kolmogorov's system, we can

calculate the necessary indexes of control quality for

the command-programming contour. Basic indexes

of this contour are the time interval when the

temporal program control can be fulfilled without a

change of TP, i.e., the duration of the independent

operating of the spacecraft for this contour (has to be

maximized) and the duration of BCC and GCC

interactions when loading TP for the next interval of

independent operation of the spacecraft (has to be

minimized). Mathematically these can be described

as follows:

T = P

/(

P

) is an average time of TP

fulfillment with BCC;

= (P

+ P

)/( 

P

) – an average time of BCC

interaction with GCC when TP is loading;

= (P

+ P

)/P

(

+ 

) – an average

time from the start of TP computation till the start of

TP fulfillment by BCC.

The last indicator also has to be minimized.

All these indicators have to be optimized through

the appropriate choice of the operations intensities

that are the parameters of the software-hardware

equipment included in the control system.

Corresponding optimization problem has the same

properties as described above.

5 MODELS GENERALISATION

We described above the simplified models of two

control contours in order to demonstrate the

modeling technique. The developed models are not

adequate for the use in the spacecraft control system

design process because of the unrealistic assumption

of GCC reliability.

If we suppose the GCC can fail then we have to

add the states when GCC fails while the system is in

any state. Let us consider the model of the

technological control contour with an unreliable

GCC which is assumed to be a single unit without

any subsystems, i.e., we will model the whole GCC

malfunctioning if any of its subsystems fails. Figure

3 shows the corresponding states graph with 10

nodes and 27 transitions that seems simple enough

for analysis. However, five new nodes with

numeration such as 6-12 or 13-19 represent states

where at least one of GCC subsystems failed.

Figure 3: States graph of Markov chain for the model of

the technological control contour with an unreliable GCC.

GCC in our problem description consists of three

subsystems groups – TCR stations, data

communication subsystem, and MCC equipment.

Considering all three groups as one unit, we will

have three GCC subsystems. If any of them can fail,

the new nodes and possible transitions will have a

view as it is shown in the Figure 4.

We will not describe the meaning of all notion in

details, recall that 

indicate the intensities of

subsystems failures and 

indicate the intensities of

subsystems being restoring by BCC (for PLE) or

GCC (for all subsystems including itself).

Not all transitions are depicted in this figure. The

whole states graph for this case consists of 40 states

and 146 transitions and is schematically depicted in

Figure 5. Corresponding Kolmogorov's equation

system contains 40 lines.

Spacecrafts' Control Systems Effective Variants Choice with Self-configuring Genetic Algorithm

Under the same conditions, the states graph for

the command-programming contour consists of 96

states and more than 300 transitions and cannot be

shown here.

Figure 4: States graph of Markov chain for description of

GCC failures while spacecraft remains reliable (state 1).

Figure 5: States graph of Markov chain for modeling

technological control contour with unreliable GCC

subsystems.

Going deeper into the details we must continue

dividing the subsystems groups (TCR stations,

telecommunication system, MCC) in parts. Then we

must unify models of all contours of the spacecraft

and models of identical contours of different

spacecrafts of the orbital group. Additionally, in

some cases we cannot use simple Markov chain

models and need a more sophisticated simulation

models. Certainly, this work cannot be done without

an adequate computation tool.

In the next stage of our research we have

developed and implemented a decision support

system for spacecraft control systems modeling with

stochastic processes models. This DSS suggests

questions to aerospace engineers designing

spacecraft control systems in their terms relative to

system structure, its subsystems, possible states and

transitions, executed operations, etc. Giving the

answers to these questions the DSS generates the

necessary data structure, the lists of states and

transitions with their descriptions in designer terms

and definitions, Kolmogorov's equations system, etc.

It can also depict the states graph in simple cases

when there are not too many states and transitions.

Working windows of this decision support system is

shown in Figure 6.

Figure 6: Working windows of DSS for control systems

modeling.

This DSS is able also to solve optimization

problems with some adaptive search algorithms.

As has been stressed above, optimization

problems arising in the described situation are hard

to solve. That is why we suggest here using our

modified genetic algorithm.

6 OPTIMIZATION

ALGORITHMS DESCRIPTION

Evolutionary algorithms (EA), the best known

representatives of which are genetic algorithms

(GA), are well known optimization techniques based

on the principles of natural evolution (Eiben, Smith,

2003). Although GAs are successful in solving many

real world optimization problems (Haupt, Haupt,

2004), their performance depends on the selection of

the GA settings and tuning their parameters (Eiben,

Hinterding and Michalewicz, 1999). GAs usually

use a bit-string solution representation, but other

decisions have to be made before the algorithm can

run. The design of a GA consists of the choice of

variation operators (e.g. recombination and

mutation) that will be used to generate new solutions

from the current population and the parent selection

operator (to decide which members of the population

ICINCO 2012 - 9th International Conference on Informatics in Control, Automation and Robotics

are to be used as inputs to the variation operators), as

well as a survival scheme (to decide how the next

generation is to be created from the current one and

outputs of the variation operators). Additionally, real

valued parameters of the chosen settings (the

probability of recombination, the level of mutation,

etc.) have to be tuned (Eiben et al., 1999).

The process of settings determination and

parameters tuning is known to be a time-consuming

and complicated task. Much research has tried to

deal with this problem. Some approaches tried to

determine appropriate settings by experimenting

over a set of well-defined functions or by theoretical

analysis. Another set of approaches, usually

applying terms like "self-adaptation" or "self-

tuning", are eliminating the setting process by

adapting settings through the algorithm execution.

There exist much research devoted to "self-

adapted" or "self-tuned" GA and authors of the

corresponding papers determine similar ideas in very

different ways, all of them aimed at reducing the

role of human expert in algorithms designing.

The main idea of the approach used in this paper

relies to automated selecting and using existing

algorithmic components. That is why our algorithms

might be called as self-configuring ones.

In order to specify our algorithms more

precisely, one can say that, according to (Angeline,

1995) classification, we use dynamic adaptation on

the level of population (Meyer-Nieberg and Beyer,

2007). The probabilities of applying the genetic

operators are changed "on the fly" through the

algorithm execution. According to the classification

given in (Gomez, 2004) we use centralized control

techniques (central learning rule) for parameter

settings with some differences from the usual

approaches. Operator rates (the probability to be

chosen for generating off-spring) are adapted

according to the relative success of the operator

during the last generation independently of the

previous results. This is why our algorithm avoids

problem of high memory consumption typical for

centralized control techniques (Gomez, 2004).

Operator rates are not included in individual

chromosome and they are not subject to the

evolutionary process. All operators can be used

during one generation for producing off-spring one

by one.

Having in mind the necessity to solve hard

optimization problems and our intention to organize

GA self-adaptation to these problems, we must first

improve the GA flexibility before it can be adapted.

For this reason we have tried to modify the most

important GA operator, i.e., crossover.

The uniform crossover operator is known as one

of the most effective crossover operators in

conventional genetic algorithm (Syswerda, 1989; De

Jong, Spears, 1991). Moreover, nearly the

beginning, it was suggested to use a parameterized

uniform crossover operator and it was shown that

tuning this parameter (the probability for a parental

gene to be included in off-spring chromosome) one

can essentially improve "The Virtues" of this

operator (De Jong and Spears, 1991). Nevertheless,

in the majority of cases using the uniform crossover

operator the mentioned possibility is not adopted and

the probability for a parental gene to be included in

off-spring chromosome is given equal to 0.5 (Eiben

and Smith, 2003; Haupt and Haupt, 2004).

Thus it seems interesting to modify the uniform

crossover operator with an intention to improve its

performance. Desiring to avoid real number

parameter tuning, we suggested introducing

selective pressure on the stage of recombination

(Semenkin and Semenkina, 2007) making the

probability of a parental gene to be taken for off-

spring dependable on parent fitness values. Like the

usual GA selection operators, fitness proportional,

rank-based and tournament-based uniform crossover

operators have been added to the conventional

operator called here the equiprobable uniform

crossover.

Although the proposed new operators, hopefully,

give higher performance than the conventional

operators, at the same time the number of algorithm

setting variants increases that complicates

algorithms adjusting for the end user. That is why

we need suggesting a way to avoid this extra effort

for the adjustment.

With this aim, we apply operators’ probabilistic

rates dynamic adaptation on the level of population

with centralized control techniques. To avoid real

parameters precise tuning, we use setting variants,

namely types of selection, crossover, population

control and a level of mutation (medium, low, high).

Each of these has its own probability distribution.

E.g., there are 5 settings of selection – fitness

proportional, rank-based, and tournament-based with

three tournament sizes. During the initialization all

probabilities are equal to 0.2 and they will be

changed according to a special rule through the

algorithm’s execution in such a way that a sum of

probabilities should be equal to 1 and no probability

could be less than a preconditioned minimum

balance. The list of crossover operators includes 11

items, i.e., 1-point, 2-point and four uniform

crossovers all with two numbers of parents (2 and

7). The "idle crossover" is included in the list of

Spacecrafts' Control Systems Effective Variants Choice with Self-configuring Genetic Algorithm

crossover operators to make crossover probability

less than 1 that is used in conventional algorithms to

model "childless couple".

When the algorithm has to create the next off-

spring from the current population, it firstly has to

configure settings, i.e. to form the list of operators

with the use of the probability operator distributions.

Then the algorithm selects parents with the chosen

selection operator, produces an off-spring with the

chosen crossover operator, mutates this off-spring

with the chosen mutation probability and puts it into

the intermediate population. When the intermediate

population is filled, the fitness evaluation is

executed and operator rates (the probabilities to be

chosen) are updated according to the operator

productivity. Then the next parental population is

formed with the chosen survival selection operator.

The algorithm stops after a given number of

generations or if another termination criterion is met.

The productivity of an operator is the ratio of the

average off-springs fitness obtained with this

operator and the off-spring population average

fitness. The successful operator, having maximal

productivity, increases its rate obtaining portions

from other operators. There is no necessity for extra

computer memory to remember past events and the

reaction of updates are more dynamic.

7 ALGORITHMS

PERFORMANCE EVALUATION

The performance of a conventional GA with three

additional uniform crossover operators has been

evaluated on the usual test problems for GA (Finck,

Hansen, Ros, and Auger, 2009). Results are given in

Table 1 below.

Table 1: Results of GA performance evaluation.

Crossover

Average performance

1-point

[0.507, 0.915] / 0.760

2-point

[0.132, 0.821] / 0.479

[0.645, 0.957] / 0.834

[0.309, 0.919] / 0.612

[0.269, 0.938] / 0.657

[0.624, 0.974] / 0.839

Table 1 contains the reliability of the algorithms

averaged over the 14 test problems from (Finck,

Hansen, Ros, and Auger, 2009) each solved 1000

times, and over all settings of the other (except

crossover) operators (selection, mutation, etc.). The

reliability is the percentage of the algorithm’s runs

that give satisfactorily precise solutions. In Table 1,

row headers "1-point, 2-point, UE, UT, UP, UR"

indicate the type of crossover, respectively, 1-point,

2-point, uniform equiprobable, uniform tournament-

based, uniform fitness proportional and uniform

rank-based crossovers.

Numbers in brackets demonstrate the variance of

these indicators. The first number in brackets is the

minimal value among the 14 tests; the second

number in brackets is the maximal value among the

14 tests. The last number is the corresponding

indicator averaged over 14 test functions.

After multiple runs and statistical processing of

the results, the following observations were found

(in terms of algorithm reliability). The best variants

are the new rank-based and conventional

(equiprobable) uniform operators. Tournament-

based crossover seems to be weak but it is the only

operator having maximum reliability of 100% on

some test problems where other operators fail.

Table 2: Comparison results of SelfCGA and problem

single best algorithms.

Crossover

Average

Min

Max

0.818

0.787

0.894

SelfCGA

0.886

0.841

0.808

0.903

SelfCGA

0.866

0.901

0.887

0.921

SelfCGA

0.901

0.925

0.877

0.959

SelfCGA

0.976

0.950

0.901

1.00

SelfCGA

1.000

0.953

0.861

0.999

SelfCGA

1.00

0.897

0.832

0.927

SelfCGA

0.878

0.741

0.667

0.800

SelfCGA

0.830

0.967

0.917

0.983

SelfCGA

0.987

0.853

0.803

0.891

SelfCGA

0.884

0.821

0.734

0.888

SelfCGA

0.892

0.833

0.765

0.881

SelfCGA

0.897

0.956

0.902

0.998

SelfCGA

1.000

0.974

0.935

0.999

SelfCGA

1.000

The next stage in evaluating the algorithms is a

comparison with the proposed self-configuring GA

(SelfCGA). Below in Table 2 one can find the

ICINCO 2012 - 9th International Conference on Informatics in Control, Automation and Robotics

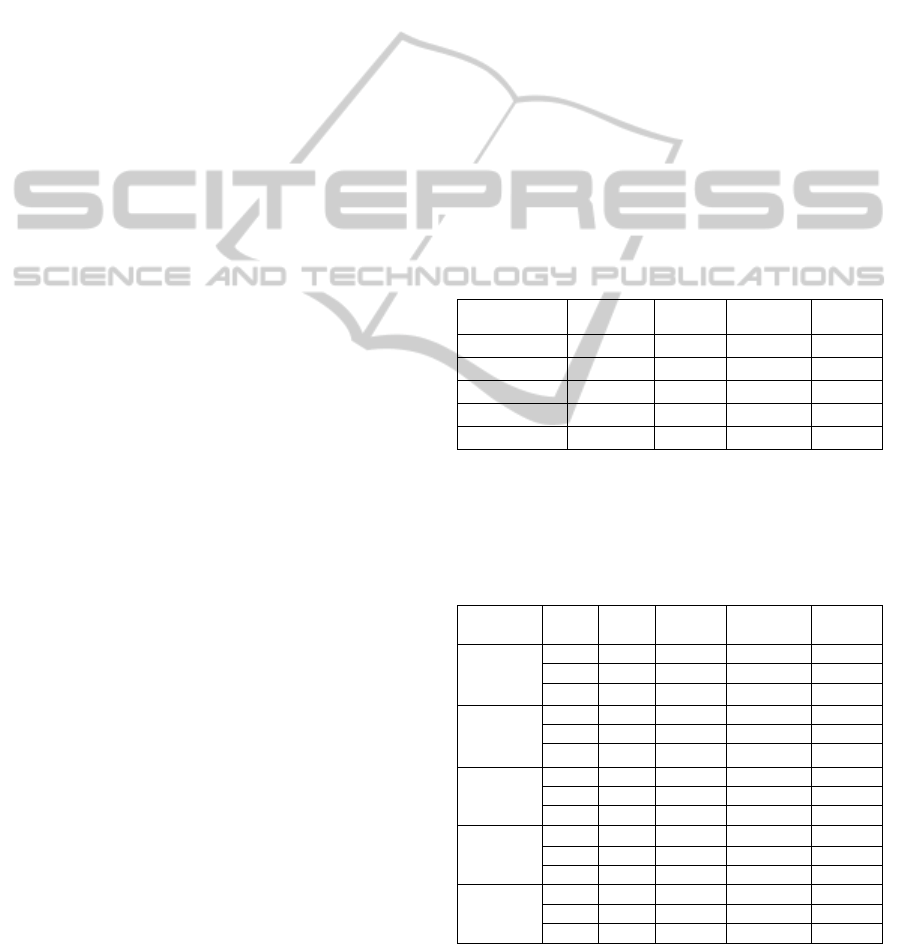
results comparing SelfCGA with the single best

algorithm having had the best performance on the

corresponding problem.

Saying "single" algorithm, we mean the group of

algorithms with the same crossover operator but

with all variants of other settings. The average

reliability of this "single" algorithm is averaged over

all possible settings. "Min" and "Max" mean GA

settings given the worst and the best performance on

the corresponding test problem.

Analyzing Table 3, we can see that in four cases

(1, 2, 3, 10, numbers are given in italics) SelfCGA

demonstrates better reliability than the average

reliability of the corresponding single best algorithm

but worse than the maximal one. In one case (7

problem), the single best algorithm (with

tournament-based uniform crossover) gives better

average performance than SelfCGA. In the

remaining 9 cases (numbers are given in bold)

SelfCGA outperforms even the maximal reliability

of the single best algorithm.

Having described these results, one can conclude

that the proposed way of GA self-configuration not

only eliminates the time consuming effort for

determining the best settings but also can give a

performance improvement even in comparison with

the best known settings of conventional GA. It

means that we may use the SelfCGA in real world

problems solving.

8 SELF-CONFIGURING

GENETIC ALGORITHM

APPLICATION IN

SPACECRAFT CONTROL

SYSTEM DESIGN

The described algorithm Self-CGA is a suitable tool

for the application in hard optimization problems

that arise in spacecraft control systems design.

First of all we evaluate its performance on the

simplified models of technological and command-

programming control contours with 5 states.

To choose an effective variant of the

technological control contour we have to optimize

the algorithmically given function with 6 discrete

variables. The optimization space contains about

1.67∙10

variants and can be enumerated with an

exhaustive search within a reasonable time. In such a

situation, we know the best (k

) and the worst (k

)

admissible values of indicators. Executing 100 runs

of the algorithm, we will also know the worst value

of indicators (k

) obtained as a run result. The best

result of the run should be (k

) if the algorithm finds

it. We use 20 individuals in one generation and 30

generations for one run. This means the algorithm

will examine 600 points of the optimization space,

i.e. about 0.0036% of it. As the indicators of the

algorithm performance we will use the reliability

(the percentage of the algorithm’s runs that give the

exact solution k

); maximum deviation MD (the ratio

of k

- k

and k

in percentage to the last); and relative

maximum deviation RMD (the ratio of k

- k

and k

in percentage to the last). The comparison is made

for 5 algorithms, namely 4 conventional GAs with

new uniform crossover operators (UE, UR, UP, UT)

and SelfCGA. For conventional GAs, the results are

given for the best determination of all other settings.

In Table 3 below, the results are shown together

with the estimation of the computational efforts (the

number of generations needed to find the exact

solution averaged over successful runs, “Gener.”).

Table 3: Algorithm reliability comparison for

technological control contour model with 5 states

(spacecraft readiness coefficient).

Algorithm

Reliability

MD (%)

RMD (%)

Gener.

0.89

0.0021

0.3576

0.92

0.0017

0.2895

0.84

0.0024

0.4087

0.97

0.0009

0.1533

SelfCGA

0.98

0.0003

0.051

Similar evaluations for all 3 indicators of the

command-programming contour are given in Table

4 below.

Table 4: Algorithm reliability comparison for command-

programming control contour model with 5 states.

Algorithm

Ind.

Rel.

MD (%)

RMD (%)

Gener.

0.87

6.431

9.028

0.76

0.956

3.528

0.83

13.392

26.01

0.95

3.987

5.6

0.93

0.341

1.258

0.93

11.347

22.04

0.79

6.667

9.359

0.71

1.156

4.266

0.74

16.321

31.7

0.91

4.873

6.84

0.81

0.956

3.528

0.86

13.392

26.01

SelfCGA

0.99

3.245

4.555

0.96

0.1226

0.4524

0.98

9.987

19.397

The difference exists in the optimization

problem size. 600 evaluations of the objective

function correspond to 0.057% of the whole

Spacecrafts' Control Systems Effective Variants Choice with Self-configuring Genetic Algorithm

optimization space as the model has only 5 discrete

variables (about 10

variants).

From Table 3 and Table 4 one can see that Self-

CGA outperforms the alternative algorithms for all

problem statements and with all performance

measures.

Now we have to evaluate the performance of the

suggested algorithm on generalized models which

have much higher dimensions.

The optimization model for the technological

control contour has 11 discrete variables. The

corresponding optimization space contains about

1.76∙10

points and cannot be enumerated with an

exhaustive search especially if one recalls that the

examination of one point includes solving a linear

equations system with 40 variables. The best (k

)

and the worst (k

) admissible values of indicators

cannot be given and we use here their best known

evaluations after multiple runs consuming much

computational resources. Nevertheless, we still can

try to obtain the resulting table similar to Table 3

with statistical confidence. For the algorithms

performance evaluations we use 40 individuals for

one generation and 80 generation for one run that

examines about 1.82∙10

-7

% of the search space

examination. Results of numerical experiments are

summarized in Table 5.

Table 5: Algorithm reliability comparison for

technological control contour model with 40 states

(spacecraft readiness coefficient).

Algorithm

Reliability

MD (%)

RMD (%)

Gener.

0.79

0.0115

0.2178

0.86

0.0099

0.1875

0.73

0.0121

0.2292

0.87

0.0095

0.1799

SelfCGA

0.90

0.0092

0.1742

For the last problem, i.e. for the model of the

command-programming control contour with 96

states and more than 300 transitions, we cannot give

detailed information as we did above. This problem

has 13 variables and contains 4.5∙10

points in the

optimization space. It requires enormous

computational efforts to find reliable evaluations of

the necessary indicators. Instead, we give a smaller

table without MD and RMD measures. It gives us

some insight on the comparative reliability of the

investigated algorithms. The algorithms performance

evaluation requires the examination of 2.2∙10

-10

% of

the search space (100 individuals and 100

generations). Results averaged over 20 runs are

summarized in Table 6.

Table 6: Algorithm reliability comparison for command-

programming control contour model with 96 states.

Algorithm

Indicator

Reliability

Generation

0.76

0.67

0.75

0.84

0.81

0.84

0.70

0.59

0.63

0.83

0.72

0.77

SelfCGA

0.91

0.87

0.89

Table 5 and Table 6 show that the Self-CGA

outperforms all alternative algorithms.

When solving these problems for real we only

need one run, but that one run requires much more

computation power than any single run above.

9 CONCLUSIONS

In this paper, the mathematical models in the form

of Markov chains have been developed and

implemented for choosing effective variants of

spacecraft control contours. These models contain

tens of states and hundreds of transitions that make

the corresponding optimization problems hard to

solve.

It is suggested to use the genetic algorithms in

such a situation because of their reliability and high

potential to be problem adaptable. As GAs

performance is highly dependent on their setting

determination and parameter tuning, the special self-

configuring GA is suggested that eliminates this

problem. The high performance of the suggested

algorithm is demonstrated through experiments with

test problems and then is validated by the solving

hard optimization problems. The self-configuring

genetic algorithm is suggested to be used for

choosing effective variants of spacecraft control

systems as it is very reliable and requires no expert

knowledge in evolutionary optimization from end

users (aerospace engineers). We did not try to

implement the best known GA with optimal

configuration and optimally tuned parameters.

Certainly, one could easily imagine that the much

better GA exists. However, it is a problem to find it

for every problem in hand. The way of the self-

configuration proposed in this paper that involves all

ICINCO 2012 - 9th International Conference on Informatics in Control, Automation and Robotics

variants of all operators can be easily expanded by

adding new operators or operator variants. The self-

configuring process monitoring gives the additional

information for further SelfCGA improving. E.g., if

the high level mutation is always the winner among

mutation variants then we can add some higher level

mutation operators in the competitors list instead of

lower level variants. Another example is the

possibility of 1-point and 2-point crossovers

removing from the crossover operators list that was

evident in our experiments.

The future research includes also not only

direct expansion in using the simulation models and

multicriterial optimization problem statements but

also the improvement of Self-CGA adaptability

through the population size control and adoption of

additional operators and operator variants.

ACKNOWLEDGEMENTS

The research is supported through the Governmental

contracts № 16.740.11.0742 and № 11.519.11.4002.

The authors are deeply grateful to Dr. Linda Ott,

a professor at the Technological University of

Michigan, for her invaluable help in improving the

text of the article.

REFERENCES

Angeline, P. J., 1995. Adaptive and self-adaptive evolutionary

computations. In: Palaniswami M. and Attikiouzel Y.,

editors, Computational Intelligence: A Dynamic Systems

Perspective, pp. 152–163. IEEE Press.

De Jong, K. A., Spears, W., 1991. On the Virtues of

Parameterized Uniform Crossover. In: Richard K.

Belew, Lashon B. Booker, editors, Proceedings of the

4th International Conference on Genetic Algorithms,

pp. 230-236. Morgan Kaufmann.

Eiben, A. E., Smith, J. E., 2003. Introduction to

evolutionary computing. Springer-Verlag, Berlin,

Heidelberg.

Eiben, A. E., Hinterding, R., and Michalewicz, Z., 1999.

Parameter control in evolutionary algorithms. In: IEEE

Transactions on evolutionary computation, 3(2):124-141.

Finck, S., Hansen, N., Ros, R., and Auger, A., 2009. Real-

parameter black-box optimization benchmarking

2009: Presentation of the noiseless functions.

Technical Report 2009/20, Research Center PPE.

Gomez, J., 2004. Self-Adaptation of Operator Rates in

Evolutionary Algorithms. In Deb, K. et al., editors,

GECCO 2004, LNCS 3102, pp. 1162–1173.

Haupt, R. L., Haupt, S. E., 2004. Practical genetic

algorithms. John Wiley & Sons, Inc., Hoboken, New

Jersey.

Meyer-Nieberg, S., Beyer, H.-G., 2007. Self-Adaptation in

Evolutionary Algorithms. In: F. Lobo, C. Lima, and Z.

Michalewicz, editors, Parameter Setting in

Evolutionary Algorithm, pp. 47-75.

Semenkin, E. S., Semenkina, M. E., 2007. Application of

genetic algorithm with modified uniform

recombination operator for automated implementation

of intellectual information technologies. In: Vestnik.

Scientific Journal of the Siberian State Aerospace

University named after academician M. F. Reshetnev.

– 2007. – Issue 3 (16). – Pp. 27-32. (In Russian,

abstract in English).

Syswerda, G., 1989. Uniform crossover in genetic

algorithms, In: J. Schaffer, editor, Proceedings of the

International Conference on Genetic Algorithms,

pp. 2-9. Morgan Kaufmann.

Spacecrafts' Control Systems Effective Variants Choice with Self-configuring Genetic Algorithm