Modified Hybrid Evolutionary Strategies Method for Termination

Control Problem with Relay Actuator

Ivan Ryzhikov

and Eugene Semenkin

Institute of Computer Sciences and Telecommunication, Siberian State Aerospace University,

Krasnoyarskiy Rabochiy Ave., 31, 660014, Krasnoyarsk, Russia

Keywords: Termination Control Problem, Evolutionary Strategies, Relay Control, Two-point Boundary Problem,

Dynamic Systems.

Abstract: The termination control problem, i.e., the problem with finite time and relay control function, is considered.

The proposed approach fits different control problems, e.g., problems with the fixed or free time, problems

with the set-up actuator characteristics and problems where the actuator can be tuned. The considered

system is the nonlinear dynamic one and the number of relay switch points assumed to be tuned indirectly.

To find out the solution of the given problem, the modified evolution strategies method is suggested. The

proposed approach is useful also for the non-analytical system models and systems that can be evaluated

numerically.

1 INTRODUCTION

The termination control task is the special case of

the optimal control task with the goal of finding out

a control function that would bring the system from

the given initial point to the desired point within a

finite time. We can also say, that the termination

control task is a special case of two-point boundary

values problem. Solutions of the two-point boundary

problem and termination control task are described,

for example, in (Cash and Mazzia, 2006) and

(Tewari, 2011), respectively. Due to the practical

needs, searching for the programmed control

function is restricted by the actuator characteristics.

The actuator can be an engine with uncontrolled

pull, so it posses only the values from some finite

set. As a special case, actuator can be a relay. Also,

the system itself is often nonlinear or algorithmically

represented. It is the main reason to investigate the

new method of programmed relay control

generation. For example, in the article (Aida-zade

and Anar, 2010) an approach to relay switch points

correction is given, when the control function is a

relay, and the determination of the switch points

number in the case of linear dynamic system is

fulfilled. As we can see the relay program control is

still an actual problem. But for the application of this

approach one needs at least some control function

which could be then tuned. In this study, we

consider the termination relay control problem for

nonlinear dynamic systems. Our approach does not

require any initial approximation of control function.

In the article (Kucherov et al., 2009) a method for

the relay control synthesis is proposed also for a

linear dynamic system. Generally speaking, the

methods for solving the termination control problem

with relay actuator for non-linear systems are not

well known. However, such problem statements are

very important in many significant areas, such as

aircrafts and spacecrafts control.

Moreover, every optimal control problem with

Hamiltonian linear over control is reduced to the

termination control problem with known relay

characteristics. All above is a reason for our study.

2 TERMINATION RELAY

CONTROL PROBLEM

DEFINITION

Let the system be described with nonlinear

differential equation

(,,)

xut

= ,

(1)

333

Ryzhikov I. and Semenkin E..

Modiﬁed Hybrid Evolutionary Strategies Method for Termination Control Problem with Relay Actuator.

DOI: 10.5220/0004044403330337

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 333-337

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

where

():

RRR R

⋅××→ is a vector function of

its arguments;

R∈

is a vector of system state;

______

(): , { , 1, }

uu i u

ut R U U u Ri N

→=∈= is a

piecewise continuous function;

n is the system dimension.

We need to find a control function

u(t) that

brings the system from the initial point

(0)

the end point

()

Tx=

within finite time T.

Though the piecewise continuous function fits

only special systems, the relay approach is useful for

every optimal control problem if the Hamiltonian is

linear over control:

(, ,) (, ) (, )

xpu xp xpu=+

and the control function itself is modulo limited.

Solving a problem with an ideal relay, we find

the control function with the structure

()

−∈

⎧

⎨

∈

⎩

(2)

where

I are sets of intervals determined by the

switch points and

[0, ]II T∪=

;

is the relay

amplitude.

For multilevel control problems we find a control

function with the structure

()

utI

∈

⎧

⎪

⎨

⎪

∈

⎩

(3)

where

______

,1,

iN= are intervals, determined by switch

points,

[0, ]

∅

;

______

{,1,}

UuRi N=∈ = is a control function

which posses values only from given set;

N is a number of relay positions (levels).

Let

____

:, 0,,0

ii i i

P rrrrR i kr

⎧

⎫

=<∈∀= =

⎨⎬

⎭

⎩

the set of switch points,

k be the number of switch

points chosen by user. Let

____

:1,

ll Ni k

⎧

⎫

=∈∀=

⎨⎬

⎭

⎩

be the set of indexes. Then each interval

______

,1,

iN=

for control (3) can be determined with the equation

{(, ] (,), }

ijjIj

rr fijr Pj

⋅∈∀

where

(, )

fij

⎧

⎪

⎨

≠

⎪

⎩

is an index function. For

ideal relay (2) we can describe another scheme for

the problem solving. We demand the change of sign

at every switch point. It means that all we need to

know for ideal relay are the sign of control at

and the switch points, because these characteristics

are enough to describe the control structure.

In the practice, there are two different problem

statements:

- the control problem, where the determination

of the actuator and determination of control function

are necessary. It means that we need to find the

characteristics of the actuator and programmed

control function that fit the termination control goal

within given finite time

T .

- the control problem, where the control program

determination only is necessary and when

T is

undefined.

The question about the number of switch points

determination is left open though there is an indirect

tuning of this number. First of all, if there is any

switch point

rT> then it will not result on the

control process. If researcher wants to fix the

number of switch points, there is another way to for

the set

____

:,, 0,,0

ii i i i

P rrrrRrTi kr

⎧

⎫

=<∈≤∀= =

⎨

⎬

⎭

⎩

determination in the way that all the switch points

will belong to the control interval. The second way

is determined by the feature of numerical scheme

that would be used to describe the process (1). Let

be the integration step, so

11ii

rr h

+−

−< means that

control interval

]

(

would not influent on the

system behaviour, so these control switching points

could be ignored.

Let

S be the set of parameters that determine

the control structure of the task. For multilevel relay

systems

{

}

,,SPLU= and for the reduced scheme

of the ideal relay

{

}

,(0)SPu= . If we have the

control problem with unfixed time and given relay

characteristics then

{

}

,SPL= for multilevel relay

and

{

}

SP=

for ideal relay.

Now let us consider criteria for different control

problems and ways of realization. As there are

different sets determined control problem, then the

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

334

problem itself can be reduced to the optimization

task with real variables, or the optimization task with

real and integer variables. If the time is fixed, the

criterion can be defined with the function

() () min

FS xTx

=− →

(4)

where

()

is the system (1) state at the point

, and the control function is determined by S

. If

the time is free, then the criterion is

(,) () min

FST xTx

=− →

(5)

There are also inequality constraints for both criteria

____

,1,

iii

rrrR i k

<∈∀=,

(6)

which ensure every switch point to be inside the

[0, ]T interval. It means that we use P

instead of P

that gives one more constraint:

rT< .

Let introduce a special penalty function

()

0, 0

⎧>

ϕ=

⎨

≤

⎩

and weight coefficient

. Now the constrained

minimization problem becomes the unconstrained

optimization problem. After adding the penalty

function into criteria (4) and (5), we have,

respectively

() () ( ) min

FS FS r T=+α⋅ϕ−→

(7)

(,) (,) ( ) min

FST FST r T=+α⋅ϕ−→

(8)

For the constraints

1ii

< , we can add the sum of

penalty functions

()

−

β⋅ ϕ −

∑

with weight

coefficient

to every criterion (4), (5), (7), (8). This

sum gives a penalty for violation of the constraint

________

,1,1

rri k

<=−. Adding it to criteria (4), (5), (7)

or (8) gives us unconstrained optimization problem.

3 MODIFIED EVOLUTIONARY

STRATEGIES ALGORITHM

Thus, the termination control problem was reduced

to the optimization task with one of objective

functions (4), (5), (7), (8) with real and integer

numbers. The objective function, in general case,

has no analytical form and has to be evaluated

numerically. This is why evolution-based

optimization algorithm has to be used. Genetic

algorithm (GA) does not fit to the given task,

because it needs the a priori known range for every

variable. Also, the discretization of real numbers for

GA adds extra troubles to the computation process.

The main principle of evolutionary strategies

(ES) is described in (Schwefel, 1995). Additionally,

we borrowed the operand definitions for integer

numbers from the GA. Our ES-based optimization

algorithm uses selection, recombination, mutation

and local optimization operands. The selected pair of

parents creates an offspring with given probability.

Then the offspring is mutated. The population size is

constant for all generations. The following GA

selection types were used: fitness proportional, rank

based and tournament based. Let every individual be

represented with a tuple

______

,, (),1,

ii i

d op sp fitness op i N==

where

( ) , {1,...,4}

1()

fitness op q

Fop

=∈

is the fitness function for problems (4), (5), (7), (8),

respectively,

____

,1,

op R j k∈= is the set of objective

parameters,

____

,1,

pRj k

∈=

is the set of method

strategic parameters and

N is the size of

population.

The solution of any task with criteria (4), (5),

(7), (8) determines the set of objective parameters

, where the every criterion defines sets

____

,1,4

jρ=

. Here

____

{,1,}

tRj kρ= ∈ =

is the set of switch

points,

____

{,1,}

lNj kρ= ∈ = is the set of indexes,

{}TR

=∈ is the time and

______

{,1,}

uRj Nρ= ∈ =

is the

U set. According to the nature of given sets,

standard ES recombination and mutation can be used

for

134

ρρ, and the standard GA recombination

(one-point, two-point and uniform crossover) can be

used for

The set of strategic parameters

1234

,sp sp

ρ+ρ+ρ+ρ , defines the mutation

operands.

Now we have to modify the mutation operation

for the ES adapting to our problems. Let

[0,1]

m ∈

be the mutation probability for every gene and

the Bernoulli distributed random value with

(1)

Pz m== . Then

ModifiedHybridEvolutionaryStrategiesMethodforTerminationControlProblemwithRelayActuator

335

_______________

(0, ), , 1, ( )

ii i i

op op z N sp op R i card op=+⋅ ∀∈= ;

_______________

(0,1), 1, ( )

p sp z N i card sp=+⋅ = .

Let

be the mutation probability for integer gene.

Let

be also the Bernoulli distributed value with

(1)

Pz m== ,

(0,1)ZU= be a random value that

is uniformly distributed, and

be a uniformly

distributed integer random value,

( 1) ... ( )

Pz Pz k

=== = =

. We also need a

function

(,)

fab

⎧

⎨

≥

⎩

. Each gene is mutated

(,)1

fspz = . We can now allow the strategy

parameters to affect on this mutation probability:

(1 )

iiu

op z op z z=− ⋅ +⋅,

_______________

,1, ()

op N i card op∀∈ = and

(1 ) (0,1)

sp z sp z N=− ⋅ +⋅

Next modification is fulfilled to avoid

constraints

1ii

< satisfaction. We make a special

transition from the objective parameters to the

switch points:

____

,1,

ropik

∑

, and change the

mutation operator to

(0, ) ,

ii i

op op z sp=+⋅Ν

1, ...ik= . In this case, the objective parameters will

be nonnegative and the initial population will be

generated with nonnegative individuals.

The random coordinate-wise real-valued genes

optimization has been implemented for the

algorithm performance improvement. The

optimization is fulfilled in the following way. For

every

N randomly chosen real-valued genes for

N randomly chosen individuals

N steps in

random direction with step size

h are executed.

For the numerical experiments in our study, the

parameters of the ES-based optimization procedure

were set as followed: the population size is 50, the

number of generation is 50, the recombination is set

as discrete one with the probability 0.8, the mutation

probability for every gene was set to

p . Local

improvement parameters were set as

2Nop

⋅ ,

Nop= and

5N = with 0.05

h = .

The proposed algorithm performance has been

evaluated on tens test problems and was found to be

promising.

4 TERMINATION CONTROL

PROBLEM FOR THE

SATELLITE MOTION ON

GEOSTATIONARY ORBIT

Let us consider a system that define the motion of a

satellite on the geostationary orbit:

213 3

() 2

(,) , , ,

ut x x

xt x x x x

⎛⎞

−−⋅⋅

=⋅−

⎜⎟

⎝⎠

It is necessary to reach the point

(

)

( ) 1, 0, 1,

TT=

from the initial point

(

)

(0) 1, 0, 1, 0.785x = within given finite time

T, so the satellite would come from one orbit to

another one. Actuator works as a relay

(): ,

ut R U

→ {,}

UAA

− , where

is the

engine force.

20 runs of the proposed algorithm with the given

above parameters were executed for the considered

problem. Results were averaged.

Let us set the initial number of switch points

10k

. Then for 10T

and the criterion (7) we can

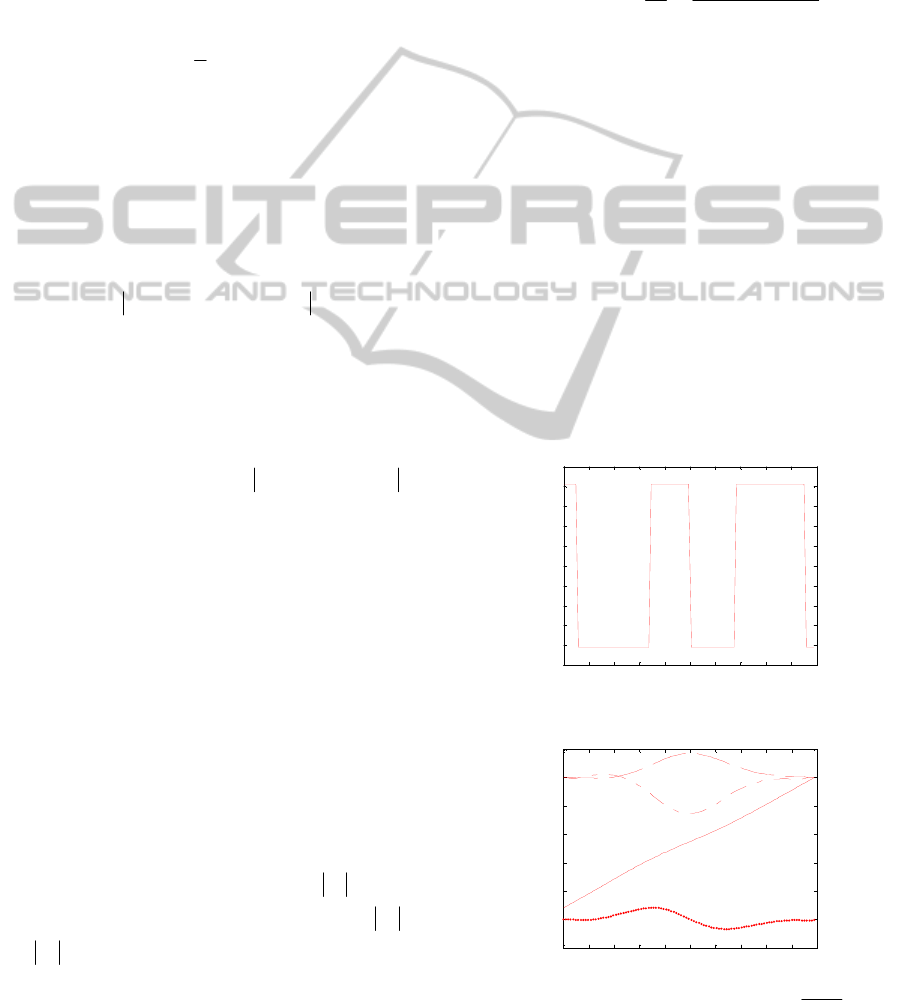
find the solution. The control function is shown on

Figure 1 and the system state is depicted on Figure

2. The system coordinates at the end point are

(

)

(10) 1.0007, 0.0064, 1.0069, 10.002x =− . The

0 1 2 3 4 5 6 7 8 9 10

-0.025

-0.02

-0.015

-0.01

-0.005

0.005

0.01

0.015

0.02

0.025

Figure 1: Control function ()ut .

0 1 2 3 4 5 6 7 8 9 10

-0.2

0.2

0.4

0.6

0.8

1.2

Figure 2: System state:

123

()

(), (), (),

xt xt xt

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

336

mean of the objective function (7) is 0.0028. The

objective function evaluations nimber was no more

than

410⋅ during every algorithm run.

For the same termination control problem but

with actuator defined by the set

{ 0.005, 0, 0.005}

U =− , we used the criterion (5)

with

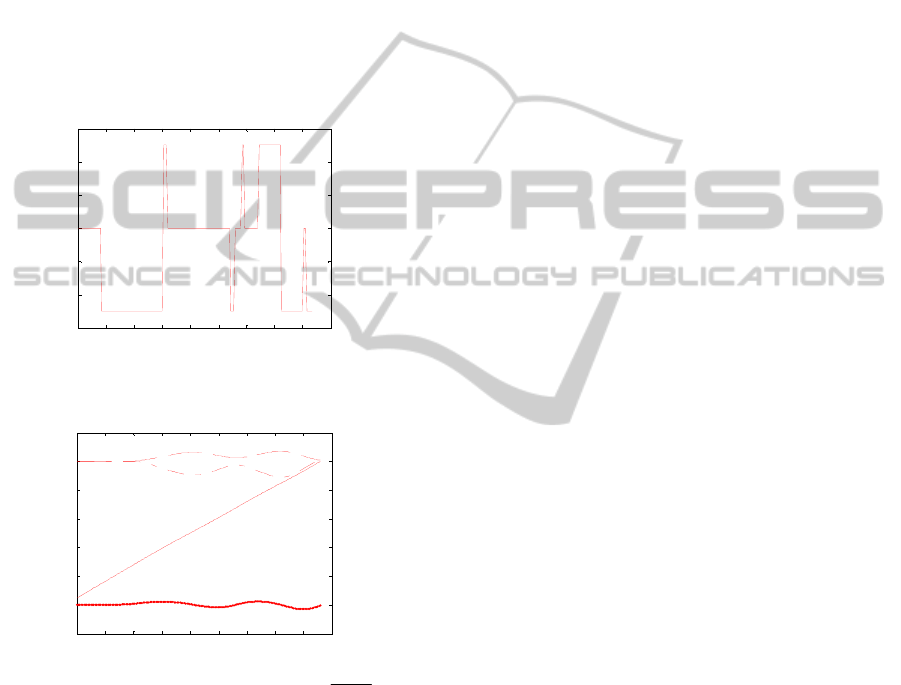
Tr= . For 20k = the following solution was

found:

17.2T = ,

()

(17.2) 1.009, 0.0065, 1.0048, 17.21x =− . The

mean of the objective function (5) is 0.018. The

objective function evaluations number was no more

than

6.25 10⋅ in every run. Similar graphics are

shown on Figures 3 and 4.

0 2 4 6 8 10 12 14 16 18

-6

-4

-2

x 10

-3

Figure 3: Control function ()ut . Time is unfixed. Three-

position relay.

0 2 4 6 8 10 12 14 16 18

-0.2

0.2

0.4

0.6

0.8

1.2

Figure 4: System state:

123

()

(), (), (),

xt xt xt

As one can see, the proposed algorithm effectively

solves the relay termination control problem for non-

linear dynamic systems. The algorithm can find the

problem solution with multilayer relay and

automatically determine the number of the relay

switch points.

5 CONCLUSIONS

In this study, the method solving the termination

control problem with the relay actuator for different

task definitions was described. The method fits if the

actuator is a multilevel relay which, in other words,

can be represented with a piecewise continuous

function with indirect tuning of the switch points

number. It is useful also if the maximum principle

reduces the control function to be the ideal relay.

The system can be described not only analytically,

but also algorithmically.

In the future the investigation of the dependence

between the number of switch points and the

algorithm efficiency should be fulfilled. For today,

there is also no certainty about what the optimization

problem statement (constrained or unconstrained)

should be chosen for the higher solution precision.

It is important also to apply the proposed algorithm

to the control problems with non-classical

constraints that appear in real control problems.

REFERENCES

Aida-zade Kamil Rajab, Anar Beybala Rahimov, 2010.

Relay Control of Nonlinear System with Uncertain

Values of Parameters. Journal of Automation and

Information Sciences. Volume 42 / Issue 7.

Cash J. R., Mazzia F., 2006. Hybrid Mesh Selection

Algorithms Based on Conditioning for Two-Point

Boundary Value Problems. Journal of Numerical

Analysis, Industrial and Applied Mathematics Vol 1,

No 1, pp 81-90.

Kucherov D.P., Vasilenko A.V., Ivanov B.P., 2009.

Dynamic system with derivative element adaptive

terminal control algorithm. Automatics.

Automatization. Electronical complexes and systems.

No 23, pp166-171.

Tewari Ashish, 2011. Advanced Control of Aircraft,

Spacecraft and Rockets, John Wiley and Sons.

Schwefel Hans-Paul, 1995. Evolution and Optimum

Seeking. New York: Wiley & Sons.

ModifiedHybridEvolutionaryStrategiesMethodforTerminationControlProblemwithRelayActuator

337