Modified Evolutionary Strategies Algorithm in Linear Dynamic

System Identification

Ivan Ryzhikov and Eugene Semenkin

Institute of Computer Sciences and Telecommunication, Siberian State Aerospace University,

Krasnoyarskiy Rabochiy Ave., 31, 660014, Krasnoyarsk, Russia

Keywords: Linear Dynamic System, Linear Differential Equation, Evolutionary Strategies, Parameters Identification

Problem, Structure Identification.

Abstract: The approach to dynamic systems modelling in the form of the linear differential equation that uses only the

system output and the control sample is presented. To develop a linear dynamic model as an ordinary

differential equation we need to know the structure of differential equation and its order, so then it would be

possible to identify parameters. It is common that measurements of the system output are distorted with a

noise. In case of the non-uniform sample we would need a special output function approximation approach

so the unit step function can be estimated. The dynamic system identification with an ordinary linear

differential equation allows solving different control tasks, determining the system state with another

control function.

1 INTRODUCTION

The solution for the given problem can be obtained

with neural networks, fuzzy logic systems or other

methods with universal structure. However,

following models would not fit if we need an

analytical form of model. There is also a possibility,

in general, to build the solution using exponential,

trigonometric and other functions that describe the

ordinary differential equation (ODE) solution, but

the control function could be given in non-analytical

form. The static model that was build as an

approximation with these functions is not as useful

and flexible as the dynamic model. Moreover, the

task would be reduced to the enumerative technique

for different combination of functions, since we do

not know the order of equation and multiplicity of

characteristic equation roots. In article (Janiczek and

Janiczek, 2010) we can see an identification method

in terms of fractional derivatives and the frequency

domain. The information about the plant is taken

from the given frequency domain and not from the

output observations. Having the model in fractional

derivatives requires special control and regulation

methods. We can also use stochastic difference

equations as in (Zoteev, 2008), and build a model

using the output observations, observations of

reaction on step excitation. This approach is partially

parameterized: the order and the functional relation

between the system state and previous states are

commonly unknown. In article (Parmar et al., 2007)

the dynamic system approximation with the second

order linear differential equations is examined. The

coefficients are determined with the genetic

algorithm. In this paper, there is the description of

the structure and parameters identification task

solution, reduction the identification task to the real

value optimization with the modified evolutionary

strategies method. The goal of approach presented in

this study is finding the order of the differential

equation and its parameters using only the distorted

output data and the optimization technique.

2 STRUCTURE

AND PARAMETERS

ESTIMATION PROBLEMS

Let us have the sample

{

}

,, , 1,

iii

yut i s= , where

∈

is the dynamic system output measurements

at a time point

t , ()

uut

is a control action. It is

also known, that the system is linear and dynamic

one, so it can be described with ODE:

618

Ryzhikov I. and Semenkin E..

Modiﬁed Evolutionary Strategies Algorithm in Linear Dynamic System Identiﬁcation.

DOI: 10.5220/0004044706180621

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 618-621

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

() ( 1)

()

ax a x axbut

−

⋅+⋅ ++⋅=⋅K ,

(0)

x= .

(1)

Here

is supposed to be known. In case of the

transition observing, we can put forward a

hypothesis about initial conditions: the system

output is known at the initial time point and the

derivative values can be set to zero, if the nature of

the problem is such or can be so approximated.

Using the sample data, we need to identify

parameters and the system order m , which is

assumed to be limited, so

,mMMN≤∈.

is a

parameter that is set by the user. It is also assumed,

that there is an additive noise

:()0,()EDξξ= ξ<∞, which results on output

measurements:

()

iii

yxt=+ξ.

(2)

Without loss of generality, one may assume that

the system is described with following equation:

() ( 1)

()

kkk

xxut

aaa

−

+⋅ ++⋅=⋅K

(3)

() ( 1)

()

ax axbut

−

+⋅ ++⋅=⋅

K .

(4)

Then we can seek the solution of the

identification task as a linear differential equation

with the order

,mMMN≤∈:

() ( 1)

ˆˆˆ ˆˆˆ

()

ax axaut

−

+⋅ ++⋅=⋅K ,

(0)

x= .

(5)

Here the vector of equation parameters

()

ˆˆˆˆ

0, , 0, , , ,

aaaaR=∈KK ,

1nM=+, has to deliver the extremum for the

functional

() () min

Ia y xt

∈

=− →

∑

(6)

In general case, the solution

()

t is computed with a

numerical integration method as the control function

may have not analytical but algorithmic form. For

the correct numerical scheme realization, let us have

a coefficient restriction for the equation (3),

0.05

a > . Otherwise, this parameter is going to be

equal to zero, so

0, 1

amm==−. This condition

prevents extra computational efforts of the

numerical evaluation scheme.

3 MODIFIED HYBRID

EVOLUTIONARY STRATEGIES

ALGORITHM FOR ORDINARY

DIFFERENTIAL EQUATION

IDENTIFICATION

The reason why the modification of an evolutionary

strategies algorithm was used is that the

identification problem leads to solve multimodal

optimization problem. The specific representation of

the equation structure results in searching not only

parameters but also the structure at the same time

that makes the criteria (6) complex. As a method for

finding the solution for ODE identification, the

hybrid modified evolutionary strategies method was

developed. Original evolutionary strategies approach

can be found in (Schwefel, 1995). Let every

individual be represented with the tuple

______

,, (),1,

ii i

op sp fitness op i N==,

where

____

,1,

op R j k∈= is the set of objective

parameters described the differential equation;

____

,1,

pRj k

∈= is the set of method strategic

parameters;

N is the population size;

(): (0,1], ()

1()

fitness x R fitness x

→=

the fitness function. The bigger fitness function

value is, i.e., the fewer criterion (6) is, the more

chances would have the individual to survive.

Proportional, rank and tournament selection

operators were chosen as selection operator types.

The algorithm produces one offspring from two

parents. The population has the same size for all

generations. Actually, these kinds of selection were

borrowed from the conventional genetic algorithm.

Let (

,op sp ) be the chromosome of the first parent

that takes part in recombination and (

,op sp

) be

the chromosome of the second parent. We consider

different recombination types for the objective

parameters (for strategic parameters it would be the

same):

- intermediate crossover (here and

further

____

1,in=

offspring

op op

;

ModifiedEvolutionaryStrategiesAlgorithminLinearDynamicSystemIdentification

619

weighed intermediate crossover:

11 2 2

() ()

offspring

itness op op fitness op op

fitness op fitness op

⋅+ ⋅

;

discrete crossover:

(1 )

offspring

iii

op z op z op=−⋅ +⋅ ;

- randomly weighted crossover. Let

(0,1)Rv U

be the uniformly distributed random value:

(1 )

offspring

iii

op op Rv op Rv=⋅+⋅−

The mutation of every offspring’s gene is

executed with the chosen probability

p . If we have

the random value

{0,1}, ( 1)

zPzp===, which is

generated for every objective gene and its strategic

parameter then

(0, )

offspring offspring offspring

ii i

op op z N sp=+⋅ ;

(0,1)

offspring offspring

sp sp z N=+⋅,

where

(, )Nmσ is normally distributed random

value with the mean m and the variance

We suggest a new operation that could increase

the efficiency of the given algorithm. For every

individual, the real value is rounded to integer. That

provides searching for solutions with near the same

structure. This modification is made to decrease the

destructive effect of the mutation on the forming the

structure.

Also for

N randomly chosen individuals and

for

N randomly chosen objective gene we make

N iterations of the local optimization with the step

h to determine the better solution. It is the random

coordinate-wise optimization. Local optimization is

executed until fitness function increases.

4 TESTING THE ALGORITHMS

WITH DIFFERENT SETTINGS

To make an investigation 50 systems were

generated. It means that for every order of the

differential equation from the first to the ninth we

have 5 different systems. Parameters of the systems

were randomly generated:

(5,5),

aU=−

)

(5,5),

bU=−

)

______

2,10,i =

___

1,ki

, where (5,5)U

−

the uniform distribution. The solution of every

system was found with the Runge-Kutta integration

method with the step

0.05

. The time of the

process was set to 5. The control function was the

step excitation and we know what was the control

for every system, so

() 1ut

. Let

{}

,, 1,/

ii i

ti Th=

be the numerical solution for the system. We take

/, 100

sThs

= points randomly. For every

system 10 runs of the algorithm were executed with

every combination of its parameters. Now, to

estimate the efficiency of different approaches we

consider the identification without any noise.

Having different types of the selection and the

crossover, we would also vary the

151

,,,1

11 11 5

⎧

⎫

∈

⎨

⎬

⎩⎭

to find out the most effective

combination of the algorithm settings. As a preset

we use population size in 50, number of populations

in 50,

50N

and

1N = with

0.05

Now we can compare the efficiency of following

algorithms: 1 – the evolutionary strategies (ES)

algorithm; 2 – ES with the local optimization, hybrid

evolutionary strategies (HES); 3 – HES with

modified mutation; 4 – HES with turning real

numbers into integer numbers; 5 - HES with

modified mutation and turning real numbers to

integer ones.

After testing the algorithms on different

samples of the systems, the efficient presets were

found: modified HES algorithm with turning the real

numbers to integer ones, 50 individuals for 50

populations,

50N

50N = and

1N = with

0.05

, the tournament selection with the

tournament size 25%, the discrete crossover and the

mutation with the probability

p =

Table 1: Mean criterion values for different algorithms and

system orders.

Algorithm

Order 1 2 3 4 5

1 0,63 0,72 0,93 0,92 0,93

2 0,69 0,73 0,74 0,79 0,85

3 0,74 0,76 0,90 0,88 0,91

4 0,69 0,79 0,99 0,98 0,99

5 0,89 0,96 0,99 0,99 0,99

6 0,76 0,80 0,82 0,83 0,86

7 0,89 0,96 0,96 0,98 0,99

8 0,85 0,89 0,93 0,91 0,93

9 0,99 0,99 0,99 0,99 0,99

10 0,99 0,99 0,99 0,99 0,99

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

620

It is important to notice that even if criterion (6)

is equal to 0, it does not mean that the model has the

same structure and parameters as the real system

structure and parameters are. For the proper

structure and parameters determination we need an

adequate sample that reflects all the transient

process. Let us take some stable systems that come

into the steady state in time

5T = . In Table 2 we

would make an efficiency investigation for the

modified HES algorithm. 20 runs of the algorithm

were made for every system. We will say that the

algorithm determines the structure and parameters if

max( ) 0.05aa−<

Table 2: The efficiency of “true” parameters estimation.

Order

ˆˆ

(max( ) 0.05)paa−<

Fitness

1 0,65 0,959344

2 0,95 0,99795

3 0,9 0,997798

4 0,95 1

5 0,8 0,996173

As we can see from Table 2, the high fitness is

not the sufficient condition for the solution found to

be true one. Let us highlight that for every solution

found from this study for stable systems, the order

was found correctly.

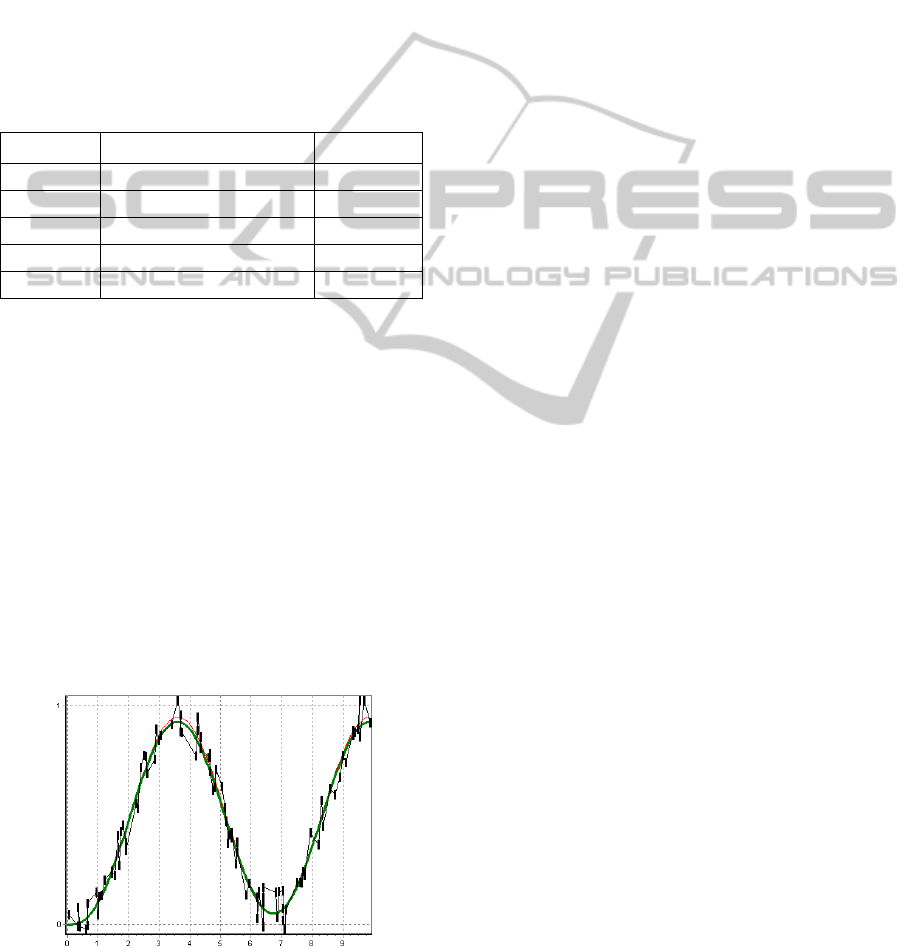
Now let us consider an example of the

identification task solving for the system of the third

order to show that even with

10M = the satisfying

solution can be found. Let the differential equation

coefficients be

()

0, ,0,1,2,1,2a = K .

With the recommended settings of the algorithm, the

absolute error mean for 20 runs is 0.063. The model

output, the sample and the real system output are

shown on the Figure 1, found parameters are

()

0, , 0, 1, 2.05, 1, 2.05a =

K .

Figure 1: Measurements, model and the real object (thin

line).

5 CONCLUSIONS

In this paper, the method of ordinary differential

equation structure and parameters identification was

described. With the proposed approach, the structure

and parameters are automatically determined.

Modifications of evolutionary strategies algorithm

increase the accuracy of model and allow solving

two tasks at the same time. It is important to note

that proposed modifications allow the algorithm to

find, in general, the right system order. The

efficiency of the algorithm for reduced identification

problem depends mostly on the sample. The better

sample represents the transient process, the better it

would be estimated. The further work with the

approach proposed will be concentrated on

investigation algorithm performance on the

problems with different noise levels, sizes of the

sample and different input functions.

REFERENCES

Janiczek T., Janiczek J., 2010. Linear dynamic system

identification in the frequency domain using fractional

derivatives. Metrol. Meas. Syst., Vol. XVII, No 2, pp.

279-288.

Parmar G., Prasad R., Mukherjee S., 2007. Order

reduction of linear dynamic systems using stability

equation method and GA. International Journal of

computer and Infornation Engeneering 1:1.

Schwefel Hans-Paul, 1995. Evolution and Optimum

Seeking. New York: Wiley & Sons.

Zoteev V., 2008. Parametrical identification of linear

dynamical system on the basis of stochastic difference

equations. Matem. Mod., Vol. 20, No 9, pp 120-128.

ModifiedEvolutionaryStrategiesAlgorithminLinearDynamicSystemIdentification

621