New Robust Controller Synthesis Optimization Methodology under Six

Sigma Constraint

J. Frechard

, D. Knittel

1,2

and J. Renaud

LGeCo, INSA, 24 Boulevard de la Victoire, 67084 Strasbourg, France

Institute of Physics and Engineering, University of Strasbourg, 17, Rue du Mar

echal Lef

ebvre, 67100 Strasbourg, France

Keywords:

Six Sigma Controller Synthesis, Design For Six Sigma, Robust Optimization, Robust Control, Hinﬁnity

Synthesis, Roll-to-roll Systems.

Abstract:

Industrial systems usually contain uncertain parameters. These uncertainties come from lack of knowledge

of physical phenomena or from evaluation difﬁculties. The stochastic behaviour of these parameters have to

be taken into account during the design process of industrial systems. To tackle with these uncertainties, the

Design for Multi-objective Six Sigma method is used. This method permits to ﬁx six sigma constraint and it

is applied on the synthesis of web tension controller for an industrial large-scale roll-to-roll system. The key

idea is to synthesize the controller in frequency domain by Hinﬁnity synthesis. Then the six sigma constraint

is ﬁxed on output web tension in time domain. The robust controller synthesis is then compared with standard

Hinﬁnity synthesis approach. This paper presents for the ﬁrst time a controller synthesis including six sigma

constraints.

1 INTRODUCTION

Real world optimization problem usually contains un-

certainties. These uncertainties come from non mod-

elled dynamics or from a lack of knowledge of the

phenomena. Moreover, some parameters can be dif-

ﬁcult to estimate and can vary with time. Due to

these uncertainties the value of performance criterion

can be very different of the expected one. Some in-

dustrial applications deal with high parameter varia-

tions depending on the processing conditions. Usual

optimization methodology only considers the design

performance without taking into account parametric

uncertainties. It is compulsory, for application with

uncertain parameters, to consider the parametric ro-

bustness of design. Performance and parametric ro-

bustness are antagonist objectives, that means that the

improvement of one of them leads to the damage of

the other. Therefore, a multi-objective approach has

to be used. The key idea is to generate a set of val-

ues of uncertain parameters following their distribu-

tion law. The ﬁtness function is calculated for each

value of the set and the mean value and standard de-

viation are given as the objectives to minimize in fre-

quency domain. Then the time domain Pareto frontier

is build and six sigma constraint is ﬁxed on it. This

paper presents for the ﬁrst time a controller synthe-

sis methodology including six sigma constraint. The

proposed approach is applied to the web tension con-

troller synthesis of a large-scale roll-to-roll system.

Roll-to-roll systems are very common in industry,

they represent a convenient way to handle web mate-

rials such as textile, paper, polymer... The web speed

and web tension are the two keys variables to be mon-

itored and controller. The focus of roll-to-roll systems

is to displace the material web at the expected speed

while keeping the web tension in an acceptable range

around the tension reference. The approach devel-

oped in this paper is applied on a large-scale roll-to-

roll plant that includes a rewinder, an unwinder, two

driven rollers, two pendulum dancers and twenty-ﬁve

idle rollers.

PI or PID controllers are commonly used for web

tension control in industrial context, (Gassmann et al.,

2011) proposes a convenient way to synthesize PI web

tension controller using ﬁxed order and structure H

∞

approach using HIFOO (H-Inﬁnity ﬁxed order opti-

mization, (Burke et al., 2006)). This synthesis method

gives good results in term of performances but the ob-

tained controllers are highly sensitive regarding web

elasticity variations.

A new robust design optimisation method is pro-

posed in this paper. For our application, the key idea

is to consider the web elasticity, Young’s modulus, as

an uncertain parameter with a normal law.

Firstly, a short state of the art of robust optimiza-

244

Frechard J., Knittel D. and Renaud J..

New Robust Controller Synthesis Optimization Methodology under Six Sigma Constraint.

DOI: 10.5220/0004045602440249

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 244-249

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tion is given. Then the proposed multi-objective ro-

bust optimization is presented in details. To ﬁnish,

the application to the large-scale roll-to-roll system is

described.

2 ROBUST OPTIMIZATION IN

ENGINEERING

Optimization of mechatronic systems is studied for

several years. A survey of the robust optimization

methods is given in (Beyer and Sendhoff, 2007).

The ﬁeld of application of robust optimization is

very large. For example, the design of antenna under

decision variable uncertainty is studied in (Ben-Tal

and Nemirovski, 2002). Mathematical programming

methods is used to deal with parametric uncertainty.

Interval programming was successfully imple-

mented for synthesizing modal control in (Khlebalin,

1994). The idea is to give the interval of variation of

each uncertain parameters and to directly take them

into account in the optimization process.

Another robust optimization method that gives

good results in control synthesis using optimal control

is the Kharitonov’s theorem presented in (Toscano

and Lyonnet, 2010). The idea is to verify the stability

of the system afterwards the control synthesis using

the characteristic polynomial of the closed loop sys-

tem.

However, the presented methods can not be imple-

mented for optimization of large-scale systems, due to

high order of the model or lack of algebraic represen-

tation of the ﬁtness function.

The design for six sigma method is studied in

(Koch et al., 2004). The major drawback of this

method is that the sigma level and the limit value

has to be ﬁxed before optimization process runs, and

therefore it is not sure that the problem is solvable.

An interesting method that permits to ﬁx the sigma

level and the limit value after the optimization process

was presented in (Shimoyama and Fujii, 2007). The

idea is to use multi objective optimization in order to

obtain a set of robust designs.

3 MULTI-OBJECTIVE ROBUST

DESIGN OPTIMIZATION

METHOD

The multi-objective design for six sigma methods

needs many evaluations of the ﬁtness function to be

efﬁcient. To measure the performance of mechatronic

K(s) G(s) W

Figure 1: Scheme of the S/KS/T synthesis with reference

model M

systems the H

∞

norm can be used. It gives good eval-

uation of the system behaviour in frequency domain

and have an acceptable computational cost.

3.1 Hinﬁnity Controller Synthesis

The H

∞

approach enables automatic synthesis of con-

trollers (Gassmann et al., 2009). The H

∞

problem

consists in ﬁnding a stabilizing controller K that min-

imize the H

∞

norm of the transfer function between a

set of exogenous inputs w and the performance out-

puts z (see Figure 1).

w→z

∞

< γ (1)

The major drawback of H

∞

approach is the high or-

der of the obtained controller. In fact, the order of the

controller is equal to the sum of the system order and

the weighting functions order. Using a model reduc-

tion approach, the controller order can not always be

reduced with guarantee of stability and performances.

In industrial applications, it is highly relevant to de-

velop a robust design algorithm for PI or PID con-

trollers adjusting. The mathematical problem seems

to be difﬁcult because ﬁxed-order controller synthe-

sis can be formulated as a nonsmooth afﬁne prob-

lem in the nonconvex cone of stables matrix. The

mathematical formulation of such a problem leads

to BMI (bilinear matrix inequalities) solving (Benla-

treche et al., 2006). Recent progress in nonsmooth

algorithm permits to develop relevant synthesis tools

like HIFOO released in 2005 (Burke et al., 2006) and

more recently hinfstruct (Apkarian and Noll, 2006).

One drawback of such approaches is that they do not

take parametric uncertainties into consideration. In

this work, genetic algorithm is used to optimize the

∞

norm of the system in order to take into account

uncertainties. The controller is synthesized with out-

put weighting functions; S/KS/T synthesis scheme is

given in Figure 1. Moreover, a reference model M

is used. The weighting functions W

, W

and the

reference model M

appear in the closed loop transfer

matrix:





− T )





(2)

where S is the sensitivity function:

S = (I + GK)

−1

(3)

NewRobustControllerSynthesisOptimizationMethodologyunderSixSigmaConstraint

245

G represents the system, K is the web tension con-

troller. T is the complementary sensitivity function:

T = I − S (4)

The weighting function W

has a high gain at low fre-

quency in order to reject low frequency disturbances.

The form of W

is as follows :

(s) =

+ ω

s + ω

(5)

where M is the maximum peak magnitude of (M

−

T ). ω

is the desired frequency bandwidth, ε

is the

allowed steady-state error.

The weighting function W

is used to avoid large

control signals and to increase the roll-off of the con-

troller output at high frequencies.

(s) =

1 + τ

k(1 + τ

, τ

> τ

(6)

The weighting function W

increases the roll-off of the

system output at high frequencies.

In industry, tension controllers are generally PI

controllers:

= K

1 + τ

(7)

where u is the control signal and ε is the error signal.

and τ

are the controller design variables to be op-

timized. The optimization problem can be formulated

as follows :

minimize ||T

∞

sub ject to λ < 0

(8)

where ||T

∞

is the weighted closed-loop H

∞

norm and λ is the maximum real part of the system

poles (for the linearised system) also called spectral

abscissa.

The uncertain parameter has now to be taken into

account in the H

∞

synthesis.

3.2 Robust Controller Synthesis using

Hinﬁnity Approach

Robust optimization methodology used in this work

is based on the six-sigma concept introduced by Mo-

torola (Tennant, 2001). The aim is to keep a perfor-

mance index in an acceptable range for a variation of

uncertain parameters of ±6σ, with σ the standard de-

viation. In fact, a six sigma constraint corresponds

to 0.002 defects per millions. In order to solve such

problem, the Design For Multi-Objective Six Sigma

(DFMOSS) described in (Koch et al., 2004) is used.

This methodology was successfully applied in the do-

main of ﬂying vehicule in (Shimoyama and Fujii,

2007) and in the domain of land vehicule (Koch et al.,

2004).

Considering the state-space representation of the

uncertain system:



˙x(t) = A(γ)x(t) + B(γ)u(t)

y(t) = C(γ)x(t) + D(γ)u(t)

(9)

where γ is a set of uncertain parameters with a nor-

mal distribution.

Latin hypercube method is used to generate a set

of sample points around the nominal value of uncer-

tain parameters. Then the robust H

∞

optimization

problem can be deﬁned as follows.

minimize µ

under λ < 0

(10)

where µ

is the mean of the ﬁtness function (the

∞

norm in our case) for the set of sample points and

is the standard deviation of the ﬁtness function.

This methodology permits to obtain the robust Pareto

frontier and then to ﬁx the sigma level and the up-

per limit constraint after optimization. To deal with

this optimization problem, the MOGA-II algorithm

is used in the modeFRONTIER commercial software

environment.

3.3 Time Domain Pareto Building

The H

∞

optimization process is used to guarantee the

frequency domain system behaviour. Moreover the

∞

norm has a very low computational cost. Never-

theless, time domain optimization allows to take into

account the plant non-linearities. It is therefore com-

pulsory to use simulation of the nonlinear model of

the system. Therefore the pseudo-Pareto frontier in

time domain is also build and the six σ constraint

can be applied on it. The non dominated point in

frequency domain can not be used alone. In fact, a

Pareto optimal design in frequency domain (where the

linear model is used), does not guarantee to obtain a

Pareto optimal design in time domain (where the non-

linear model is used. This is also true for the linear

model). A set of points close to the Pareto frontier in

frequency domain has to be chosen and simulated in

order to build the pseudo-Pareto frontier in time do-

main. To select the points useful for time simulation,

an area of the search space is deﬁned. The two anchor

points (an anchor point is a point where one objective

is minimum) are chosen to form a rectangle, this area

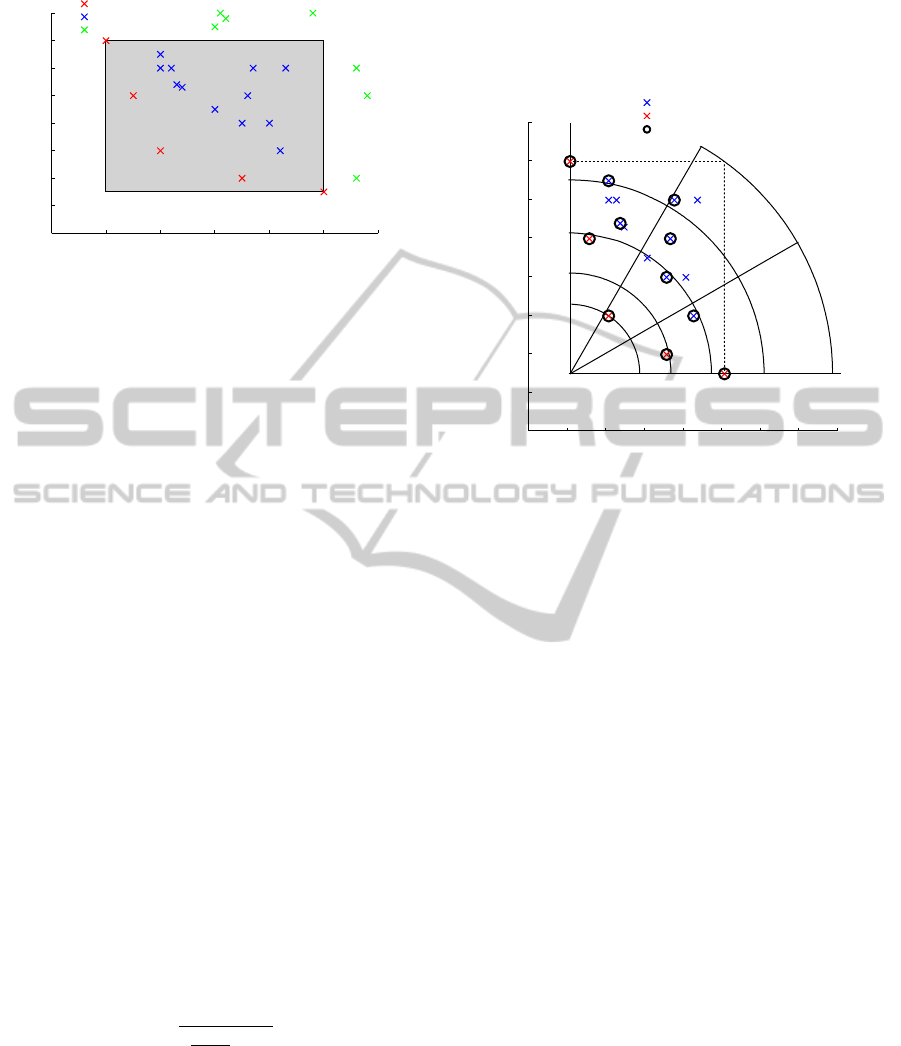
can be seen in Figure 2.

If this area contains an acceptable number of de-

signs, about a hundred, they will be all simulated.

Otherwise only some of them have to be selected. In

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

246

0 1 2 3 4 5 6

Pareto Frontier

Design to Simulate

Other Design

Figure 2: Area around the Pareto obtained from frequency

domain optimization.

order to chose the designs for non-linear time simu-

lation we propose to cut the objective space in differ-

ent areas and to select a point in each of them. The

simulation of the non-linear model can be very time

consuming and therefore the number of designs has

to be limited to one hundred. Moreover, the Pareto

proximity has to be taken into account: a point close

to the Pareto frontier should have a higher probability

to be chosen that a point far from the Pareto frontier.

A method to divide the search space around the

Pareto frontier using circles and lines is proposed.

Two points in the objective space have to be de-

ﬁned. Firstly, the UTOPIA point which is an unattain-

able design where all the objectives are minimum.

Secondly, the NADIR point is the opposite of the

UTOPIA point, it corresponds to the point with the

value of the ﬁrst objective when the second is mini-

mum and vice-versa (see ﬁgure 3). These two points

are used for the ﬁrst step of the cut-out method; the

circular areas cut-out. The UTOPIA point is taken

as circle center, the distance between the utopia point

and the closest point is computed and used as mini-

mum value of the circle radius. The distance between

UTOPIA and NADIR points is used as maximum cir-

cle radius. To guarantee the probability of selection

of a point based on Pareto proximity, the difference

between minimum and maximum radius is divided in

several areas following a non-linear law:

= R

i−1

max

− R

min

1−n

− 1

(i−1)

(11)

where R

and R

i−1

are respectively the radius of

the considered circle and the radius of the previous

circle. n is a multiplication factor between two con-

secutive spaces, in this work n is equal to 1.3. nb is

the number of circles.

The second phase of the cut-out method uses lines

in order to divide the objective space circles. The an-

gle between the utopia point and the two ANCHOR

points is divided into several areas using a linear law.

Then, in each area a point is chosen using random

search. An example of the obtained areas and selected

designs can be seen in ﬁgure 3.

0 1 2 3 4 5 6 7 8

Design in the Selection Area

Pareto Design

Design to Simulate

UTOPIA point

NADIR point

Figure 3: Example of areas and selected points provided by

the cut-out strategy (frequency domain).

The cut-out strategy permits to guarantee the dis-

persion of the simulated design around the frequency

domain Pareto (the design close to the Pareto have a

higher probability to be selected). The selected de-

signs in the frequency domain are then simulated in

time domain, using the non-linear system model.

3.4 Building of the Time Domain Pareto

Frontier

In order to evaluate performances of time domain

simulations results, many criteria can be used. IAE

(Integral of absolute error) and ISE (Integral of

squared error) are common criteria. In some appli-

cations, the derivative of the error signal can be added

to IAE or ISE criterion to minimize oscillation. In

several speciﬁc applications the error signal does not

play a major role but the maximum of the error signal

is the major criterion to minimize.

Then a set of thirty values of each uncertain pa-

rameter is generated using latin hypercube sampling.

The designs selected in the frequency domain Pareto

using the cut-out strategy are simulated for each value

of the uncertain parameters. The mean value µ

and

standard deviation σ

of the set of ﬁtness are then

calculated. Once the time domain Pareto frontier is

build, the six sigma constraint can be ﬁxed on it:

+ 6σ

< USL (12)

where USL is the upper acceptable limit of J.

NewRobustControllerSynthesisOptimizationMethodologyunderSixSigmaConstraint

247

Figure 4 shows an example of obtained time do-

main pareto frontier. The red line represents the 6

sigma constraint: the design under it respects the con-

straint (In other words, the criterion J is greater than

the USL value with a probability of only 0.002 per

million). Some applications do not need a so high re-

liability, for them lower sigma level can be used (for

example 3 sigma).

0 1 2 3 4 5 6 7

Design Simulated

Pareto Optimal Design

σ Constraint

Figure 4: Example of time domain Pareto.

For the choice of the ﬁnal design, the distance be-

tween the six σ constraint line and each design is com-

puted. The more robust design is the design with the

higher distance. The presented method can now be

applied on a complex large-scale system in order to

synthesize robust controllers.

4 APPLICATION TO

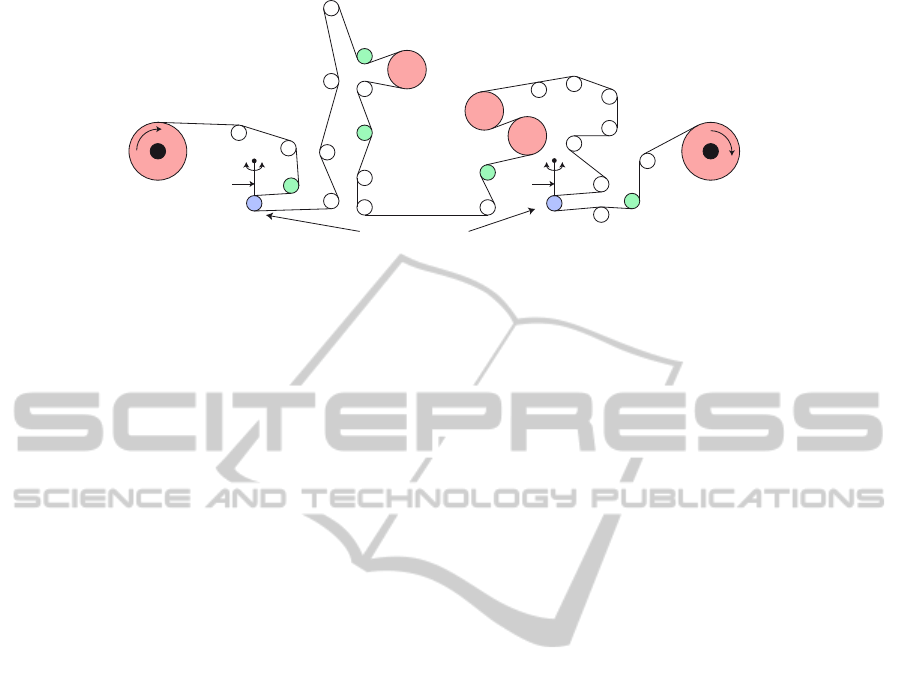
ROLL-TO-ROLL SYSTEMS

The proposed approach is applied to the synthesis

of tension controllers of an industrial roll-to-roll sys-

tem. This system is composed of four motor, two

pendulum dancers, thirty rollers and ﬁve load cells.

Its model is constructed from the equation describ-

ing the speed of each roller, the web tension between

two rollers and the pendulum dancers angular posi-

tion (Koc et al., 2002) (Gassmann et al., 2009). The

scheme of the system is given in ﬁgure 6.

The tension control of roll-to-roll systems is stud-

ied for several years. H

∞

control is used and

gives good performance (Gassmann et al., 2011)

(Gassmann et al., 2009). However, this method does

not take into account the parametric uncertainties.

The approach developped in this work has been

compared with the ﬁxed order and structure H

∞

syn-

thesis using the commercial hinfstruct algorithm (Ap-

karian and Noll, 2006) in the Matlab software envi-

ronment. The results in frequency domain are ﬁrstly

compared using the linear model, then the time do-

main simulation are compared for a variation of web

elasticity on the non-linear system model.

The frequency domain and time domain criteria

depicted below are used. The value of each criterion

for the nominal value of web elasticity E

, the mean

and standard deviation of each criterion, are calcu-

lated for the set of web elasticity values. A summary

of the results is given in table 1.

Table 1: Criteria comparison between hinfstruct and our ro-

bust design optimization

∞

) J (E

) µ

(1) 93 11 94 5 12 1.6

(2) 88 8 116 29.2 84 165

The line (1) corresponds to our presented synthe-

sis method whereas the second line marked (2) cor-

responds to the advanced synthesis using hinfstruct.

One can see that for our approach the ﬁrst two crite-

ria are a little greater. Therefore the hinfstruct gives

slightly better nominal performances ( for a ﬁxed

nominal web elasticity). However, when web elastic-

ity variations occur, our proposed methodology leads

to better results. In fact, mean values and standard

deviation of the two criteria are lower.

Then the two set of parameters are compared us-

ing non-linear model simulations. The simulation re-

sults are presented for three values of web Young’s

modulus, E

/1.5, E

and E

.1.5 in Figure 5 (interme-

diate web tension).

0 50 100

Time (Second)

Tension (Newton)

0 50 100

Time (Second)

Tension (Newton)

Figure 5: Time domain simulation.

For the hinfstruct controller synthesis approach

the system becomes unstable (lower representation

in ﬁgure 5) whereas our approach maintains good

performances (upper representation in Figure 5) with

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

248

’

RewinderUnwinder

Driven Rollers

Pendulum Dancers

Figure 6: Scheme of the system under study.

web tension errors smaller than 20 N, as expected (six

sigma design).

5 CONCLUSIONS

A new robust controller synthesis method is devel-

oped using six sigma constraint to tackle with para-

metric uncertainties. A set of values of the uncertain

parameter is computed and statical tools are used in

order to build a set of robust design. This set allows to

build the time domain Pareto in order to ﬁx six sigma

constraint in time domain. The Pareto in closed-loop

frequency domain is also calculated. The two Pareto

curves enable to select the best design.

The methodology is applied on a complex large

scale roll-to-roll model of an experimental plant. The

results are compared with advanced commercial ro-

bust controller synthesis (hinfstruct Robust control

toolbox in Matlab software environment). The sim-

ulations show that the proposed methodology leads to

more robust closed loop system performances regard-

ing the uncertain parameter variations.

Future work consist in integrating other parame-

ters in the optimization process, for example mechan-

ical parameters.

ACKNOWLEDGEMENTS

The authors thank Enginsoft France support, specially

A. Poisson, for the help supplied during the imple-

mentation of the proposed method in the modeFRON-

TIER environment.

REFERENCES

Apkarian, P. and Noll, D. (2006). Nonsmooth H

∞

synthesis.

Automatic Control, IEEE Trans. on, 51(1):71–86.

Ben-Tal, A. and Nemirovski, A. (2002). Robust optimiza-

tion : methodology and applications. Mathematical

Programming, 92(3):453–480.

Benlatreche, A., Ostertag, E., and Knittel, D. (2006). H

∞

feedback decentralized control by BMI optimization

for large-scale web handling systems. In American

Control Conference, Minneapolis, USA.

Beyer, H. and Sendhoff, B. (2007). Robust optimization : A

comprehensive survey. Computer Methods in Applied

Mechanics and Engineering, 196(33-34):3190–3218.

Burke, J. V., Henrion, D., Lewis, A. S., and Overton,

M. L. (2006). HIFOO - A MATLAB package for

ﬁxed-order controller design and H

∞

optimization.

In 5th IFAC Symposium on Robust Control Design,

Toulouse, France.

Gassmann, V., Knittel, D., Pagilla, P., and Bueno, M.

(2009). H

∞

unwinding web tension control of a strip

processing plant using a pendulum dancer. In Ameri-

can Control Conference, St. Louis, Missouri, USA.

Gassmann, V., Knittel, D., Pagilla, P. R., and Bueno, M.-A.

(2011). Fixed-order H

∞

tension control in the unwind-

ing section of a web handling system using a pendu-

lum dancer. IEEE Transactions on Control Systems

Technology, (99):1–8.

Khlebalin, N. A. (1994). Control of nonlinear and uncer-

tain systems modal control under interval uncertainty

of parameters. Computational Mathematics and Mod-

eling, 5:44–51.

Koc, H., Knittel, D., de Mathelin, M., and Abba, G. (2002).

Modeling and robust control of winding systems for

elastic webs. Control Systems Technology, IEEE

Transactions on, 10(2):197 –208.

Koch, P., Yang, R.-J., and Gu, L. (2004). Design for six

sigma through robust optimization. Structural and

Multidisciplinary Optimization, 26:235–248(14).

Shimoyama, K., O. A. and Fujii, K. (2007). Multi-objective

six sigma approach applied to robust airfoil design for

mars airplane. In 48

Structures, Structural Dynamics

and Materials Conference, Hawaii.

Tennant, G. (2001). SIX SIGMA: SPC and TQM in Manu-

facturing and Services. Gower Publishing.

Toscano, R. and Lyonnet, P. (2010). Robust static output

feedback controller synthesis using kharitonov’s the-

orem and evolutionary algorithms. Information Sci-

ences, 180:2023–2028.

NewRobustControllerSynthesisOptimizationMethodologyunderSixSigmaConstraint

249