Low-speed Modeling and Simulation of Torpedo-shaped AUVs

Bjarni Helgason

, Leifur Leifsson

, Indridi Rikhardsson

, Helgi Thorgilsson

and Slawomir Koziel

CADIA/Laboratory for Unmanned Vehicles, School of Science and Engineering, Reykjavik University, Reykjavik, Iceland

Teledyne Gavia ehf, Vesturvor 29, 200 Kopavogur, Iceland

Engineering Optimization & Modeling Center, School of Science and Eng., Reykjavik University, Reykjavik, Iceland

Keywords:

Autonomous Underwater Vehicle, Low-speed Motion, Vehicle Dynamics, Simulation, Experimental Valida-

tion.

Abstract:

Autonomous underwater vehicles (AUVs) have become important in many marine engineering applications,

such as environmental monitoring, pipeline inspections, or oceanography. For these types of applications, most

of the AUVs available in both academia and industry are shaped like a torpedo and travel at speeds of 3 knots

or higher. There is an growing interest in AUVs that are capable of performing tasks at both low-speed as well

as high speeds. Currently, many torpedo-shaped AUVs are not capable of controlled low-speed motion. This

paper presents a simulation model for the low-speed motion of torpedo-shaped AUVs. The model is capable

of simulating the surge, sway, heave, and yaw motions. The hydrodynamic forces acting on the AUV hull are

modelled using strip theory, experimental data, and computational ﬂuid dynamics. The simulation model was

implemented using a commercially available software and validated using experimental data obtained from

the Gavia AUV. The results show that the simulation model captures the AUV motion at low-speed and agrees

well with the experimental data.

1 INTRODUCTION

An autonomous underwater vehicle (AUV) is a robot

which travels underwater without requiring any input

from an operator (Fossen, 1994). The tasks and mis-

sions of AUVs are constantly evolving and becom-

ing increasingly important for commercial-, military-,

research- and hobby users. A typical commercial job

for an AUV is, e.g., to construct detailed maps of the

seaﬂoor before building subsea infrastructure in the

oil and gas industry. A typical military mission for an

AUV is to map an area and determine if there are any

mines, or to monitor a protected area for unidentiﬁed

objects. Scientists use AUVs to study lakes, the ocean

and the ocean ﬂoor.

Numerous AUVs have been developed, both in

academia, e.g., (Clark et al., 2009; Ananthakrishnan

and Decron, 2000; de Barros et al., 2008; Kennedy,

2002), and in the industry, e.g., (Allen et al., 2000).

These vehicles are of various shapes and sizes. AUV’s

intended for high-speed (higher than 3 knots) and

long-range (longer than 6 hours) missions are com-

monly torpedo-shaped with aft-mounted propulsion

and control systems (Braunl et al., 2007; Eastman

et al., 2009). AUVs designed for performing tasks at

low speeds differ, but (usually) their shapes are not

streamlined, as it is not necessary. However, they

are (normally) equipped with several thrusters for ma-

noeuvring in all directions. There is an growing inter-

est in AUVs that are capable to perform tasks at both

low- (or zero) and high-speeds (Braunl et al., 2007).

Currently, many torpedo-shaped AUVs are not capa-

ble of controlled low-speed motion.

The objective of this research is to investigate the

low-speed characteristics of torpedo shaped AUVs

and their control. In particular, we model the ve-

hicle motion at low-speed and develop a computa-

tional framework capable of simulating the vehicle

response. We use the commercially available Gavia

AUV

as a testbed (Fig. 1). The model is validated

and tuned using data from physical experiments.

Figure 1: The Gavia AUV is commercially available and

is capable of various missions, such as oceanography and

pipeline inspection.

www.gavia.is

333

Helgason B., Leifsson L., Rikhardsson I., Thorgilsson H. and Koziel S..

Low-speed Modeling and Simulation of Torpedo-shaped AUVs.

DOI: 10.5220/0004047103330338

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 333-338

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 GOVERNING EQUATIONS FOR

LOW-SPEED MOTION

We want to move the AUV in certain directions dur-

ing low-speed motion. In particular, we want to move

the AUV back and forth, up and down, to the sides,

and rotate it. Therefore, only four degrees of freedom

are required. In this section, we describe the govern-

ing equations for such motion and we develop speciﬁc

models for the system dynamics.

2.1 General Equations and Frames of

Reference

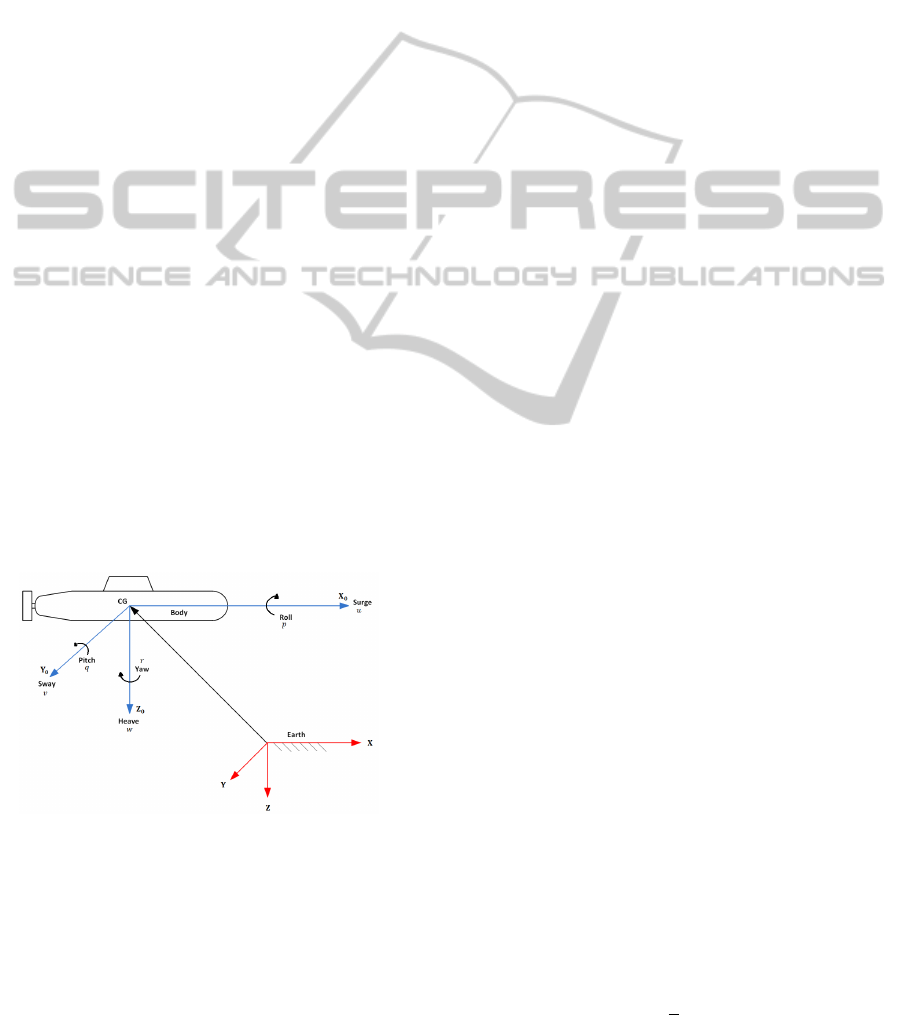
Two coordinate frames must be deﬁned to describe

the motion of underwater vehicles (Fig. 2). The mov-

ing coordinate frame X

is ﬁxed to the vehicle

and is called the body-ﬁxed reference frame and the

ﬁxed coordinate frame XY Z is the earth coordinate

system (Fossen, 1994). The ﬁxed coordinate system

is an earth coordinate system while the moving one

follows vehicle heading and location each time. The

X−axis is in line with length of vehicle and center of

gravity, where positive movement means forward and

vice versa. All movement in line with the X −axis

is surge (u is surge velocity) movement, while rota-

tion about the axis is roll (p) rotation. Axes Y and Z

then follow the X−axis as in a regular coordinate sys-

tem. Movement in line with Y -axis is sway (v is sway

velocity), while rotation about same axis is pitch (q)

rotation. Movement in line with Z-axis is heave (w is

heave velocity), while rotating about same axis is yaw

(r) rotation.

Figure 2: Coordinate systems, both body-ﬁxed and earth-

ﬁxed.

At low speed, the AUV moves in one direction at

a time. In particular, the AUV moves along the axes

of surge, sway and heave, and rotates (yaws) about

heave axis. The general governing equations of mo-

tion along each of these axes are (Fossen, 1994)



˙u − vr + wq −x

+ r

) + y

(pq − ˙r)

(pr + ˙q)] =

∑

ext

(1)



˙v − wp + ur − y

+ p

) + z

(qr − ˙p)

(qp + ˙r)] =

∑

ext

(2)



˙w − uq +vp − z

+ q

) + x

(rp − ˙q)

(rq + ˙p)] =

∑

ext

(3)

˙r +(I

− I

)pq + m [x

( ˙v − wp + ur) − y

( ˙u − vr + wg)] =

∑

ext

(4)

where m is the rigid body mass, I is the rigid body

inertia about a speciﬁc axis, x

, y

and z

are each

axis distance from the rigid body center of gravity,

ext

, Y

ext

, Z

ext

are forces acting of the vehicle in their

respective axes, and N

ext

is the moment about the

−axis.

We will now analyze each of these equations for

the low-speed motion of torpedo-shaped AUVs.

2.2 Surge Motion

The external forces acting on the AUV in the surge

direction are due to the thrust, drag and added mass.

The governing surge equation of motion, Eq. (1),

becomes, when taking into account these external

forces, as well as neglecting motion in other direc-

tions,

m ˙u = −X

˙u

˙u − D

surge

u + T

surge

, (5)

where X

˙u

is the added mass derivative for surge, D

surge

is the hydrodynamic drag for surge, and T

surge

is the

surge thrust force. Effects due to Coriolis and cen-

tripetal forces are neglected.

In this work, we estimate the added mass deriva-

tives using strip theory for slender bodies (Fossen,

1994). The added mass derivative for surge is (Hel-

gason, 2012)

˙u

' −0.1m. (6)

The hydrodynamic drag is modelled as (Wang and

Clark, 2007)

D = D

+ D

, (7)

where D

and D

are the linear and quadratic drag

terms, respectively. The linear term is determined by

experiments, and the quadratic term is

= C

surge

ρA

surge

u|u|, (8)

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

334

where C

surge

is the drag coefﬁcient for surge motion,

ρ is the water density, A

surge

is the reference area for

surge motion. The surge drag coefﬁcient is deter-

mined using computational ﬂuid dynamics (CFD) and

the resulting value is C

surge

= 0.37 (Helgason, 2012).

2.3 Sway Motion

Same type of forces act on the AUV in the sway direc-

tion as in the surge one. The governing sway equation

of motion, Eq. (2), becomes (Helgason, 2012)

m ˙v = −Y

˙v

˙v − D

sway

v + T

sway

, (9)

where Y

˙v

is the added mass derivative for sway, D

sway

is the hydrodynamic drag for sway, and T

sway

is the

sway thrust force. Strip theory yields the added mass

derivative as (Helgason, 2012)

˙v

' −πρR

L, (10)

where R is the maximum radius of the AUV hull and L

is it’s length. The drag is modelled in the same way as

for the surge motion, i.e., Eqs. (7) and (8). However,

the quadratic drag coefﬁcient in the sway direction

is estimated based on experimental data for circular

cylinder in cross-ﬂow and is taken to be C

sway

= 1.2

(White, 2008).

2.4 Heave Motion

In the heave direction, the same external forces act

on the vehicle as in the surge and sway directions,

including the gravitational and buoyancy forces. The

governing heave equation of motion, Eq. (3), is then

(Helgason, 2012)

m ˙w = −Z

˙w

˙w − D

heave

w − ( f

+ f

) + T

heave

, (11)

where Z

˙w

is the added mass derivative for heave,

heave

is the hydrodynamic drag for heave, f

is the

vehicle weight, f

is the vehicle buoyancy force, and

heave

is the heave thrust force. The added mass

derivative term Z

˙w

for heave can be assumed to be

the same as for sway, Eq. (10), because of symmetry

in the torpedo-shaped hull. For the same reason, we

use the same drag coefﬁcient value, i.e., C

heave

= 1.2.

2.5 Yaw Motion

External moments in the yaw rotational motion are

moments due to the thrusters, hull drag, and added

mass. The governing equation for yaw motion, Eq.

(2), becomes (Helgason, 2012)

˙r = −D

yaw

r +M

yaw

, (12)

Heave ModelSurge Model Sway Model

Yaw Model

Figure 3: The four non interacting models of the simulator

for each of the degrees of freedom.

where D

yaw

is the hydrodynamic drag for yaw, and

yaw

is the yawing moment due to the thrusters. The

drag is modelled using Eqs. (7) and (8). The quadratic

drag coefﬁcient is estimated based on experimental

results for cylinder in cross-ﬂow. We assume that

each half of the cylinder is in cross-ﬂow with the re-

sulting force acting in it’s center. Based on this the

drag coefﬁcient is found to by C

yaw

= 0.55 (White,

2008).

3 SIMULATOR FRAMEWORK

The simulator was built in a plain block diagram en-

vironment using Simulink (Mathworks, 2011) where

the differential equations for each degree of freedom

(DOF) presented in Section 2 were implemented. The

simulator structure is based on four non interacting

models, each corresponding to a separate DOF (Fig.

3). Motion of the AUV along each DOF is simulated

at a time and the combination of all the four models

yields a simulation of the overall motion.

Due to length limitations, the models cannot be

described in detail. However, the general structure of

each model is shown in Fig. 4. The ﬁrst block on

the left is the input signal generator. In the second

block, the thruster characteristics are deﬁned. The

main thruster at the rear is used for surge motion,

while different thrusters are used for the other DOF’s.

Input Thrusters

External

Forces

AUV

Dynamics

Output

Feedback

Figure 4: The basic block structure for each of the simula-

tion models.

The third block represents the external forces acting

on the AUV, such as drag, added mass, gravity, and

buoyancy. The fourth block represents the AUV dy-

namics, which is different for each DOF, as described

in Section 2. The block farthest to the right pro-

duces the simulation output, such as depth, heading

Low-speedModelingandSimulationofTorpedo-shapedAUVs

335

and position. The bottom block represents the feed-

back from the sensors (including any time delays). A

detailed description of each model is given in (Helga-

son, 2012).

4 EXPERIMENTAL TESTING

In order to gather data for validating and tuning the

simulator, several experiments were performed using

the Gavia AUV. In this section, we describe the exper-

imental approach and setup for open and closed loop

testing.

4.1 Approach

The simulator can handle AUV motion in surge, sway,

heave, and yaw. Therefore, data on the vehicle be-

haviour in all those directions is required for the sim-

ulator validation. Figure 5 shows where forces are

needed for each direction. The testbed AUV only

has a rear mounted propeller and can, therefore, only

move in the surge direction. Additional thrusters were

mounted on to the hull to achieve the desired motion.

For each direction, both the open and closed loop per-

formance were studied. In particular, we studied the

response as a function of the thruster load, as well as

different PID controller settings.

4.2 Setup

A pair of externally mounted thrusters were used

for the experimental testing, aside the case of surge,

where the rear mounted propeller was used. The

thrusters were installed on a bracket which was

mounted on the sides of the AUV hull as shown in Fig.

6. A plastic pipe was included in the bracket to pro-

vide buoyancy to balance the weight of the thruster.

The thrusters are manufactured by Seabotix and are

controlled by a Devantech MD22 motor controller.

Figure 7 shows a thruster mounted on the bracket.

Figure 8 shows the Gavia AUV with two thrusters

mounted on it’s side for sway testing. All tests were

performed in an indoor swimming pool of 3 m depth.

5 MODEL VALIDATION AND

TUNING

In this section, we present the results obtained in the

experiments described in Section 4 and compare them

with numerical results obtained by the model pre-

sented in Sections 2 and 3. In particular, we present

Surge

Sway

Heave

Yaw

Figure 5: Experimental setup of the forces acting on the

AUV hull for testing of each of the degree of freedom.

Figure 6: A sketch of the bracket and thrusters mounted on

the hull of the AUV.

Figure 7: An assembly of the thruster, bracket and ﬂoat.

Figure 8: The Gavia AUV with the thruster assembly

mounted on the sides during testing.

results for surge, sway, and yaw motions. The heave

model is identical to the sway model.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

336

(a)

(b)

Figure 9: Surge open loop response for the propeller at 197

rpm (a) distance as a function of time, here the cubic ﬁt is a

polynomial ﬁt to the true data used for comparison with the

simulation, and (b) velocity as a function of time.

5.1 Surge

Open loop response for surge forward motion are

shown in Fig. 9 for the propeller at 197 rpm. A multi-

plicative tuning factor was applied to the model. The

simulation model follows the experimental data for

the ﬁrst 12 seconds or so. The discontinuous shape of

the experimental data is due to a low sampling rate of

the sensors.

5.2 Sway

Open and closed loop sway responses are shown in

Fig. 10. Here the quadratic drag term was tuned with

a multiplicative constant to match the data in the open

loop response. In the closed loop test, the AUV was

translated by 80 cm.

The results show that the control system is able to

quickly reach the translated distance, but overshoots

by approximately 23 cm and converges towards the

reference value slowly. The simulator follows the ex-

perimental results quite well, but overshoots by 30

cm, and converges more quickly towards the refer-

ence value. This indicates the discrepancy between

the experimental and simulation conﬁgurations.

(a)

(b)

Figure 10: Sway responses (a) open loop with constant

thrust of 0.5, and (b) closed loop with PID values of P = 30,

I = 0, and D = 0.

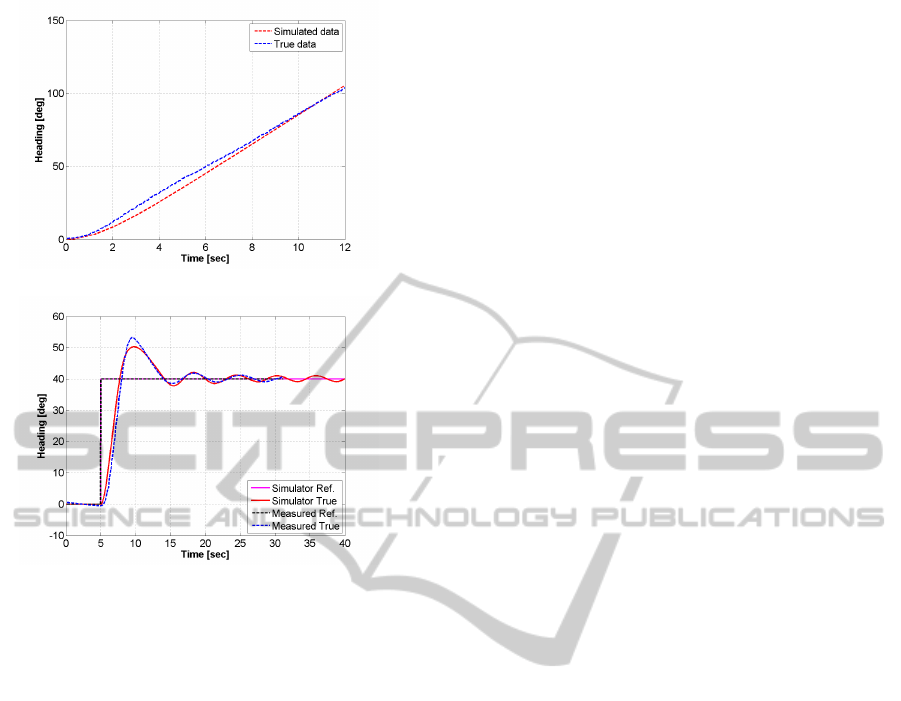
5.3 Yaw

Open and closed loop yaw responses are shown in

Fig. 11. Here, as in the case of sway, the quadratic

drag term was tuned with a multiplicative constant

to match the data in the open loop response. In the

closed loop test, the AUV was rotated by 40 degrees.

The results show that the control system quickly

rotates the AUV towards the reference value, but over-

shoots by about 14 degrees. However, it recovers

swiftly and reaches the reference value within 15 to

20 seconds. The simulation follows the data closely

throughout the data series.

6 CONCLUSIONS

A simulation model for the motion of torpedo-shaped

AUVs at low-speed was presented. The model is

based the general equations of motion for marine ve-

hicles. The hydrodynamic forces acting on the AUV

hull were modelled using strip theory, experimental

data, and computational ﬂuid dynamics. The simu-

lation model was implemented using a commercially

available software and validated using experimental

Low-speedModelingandSimulationofTorpedo-shapedAUVs

337

(a)

(b)

Figure 11: Yaw responses (a) open loop with constant thrust

of 0.5, (b) closed loop with PID values of P = 2, I = 0, and

D = 0.

data obtained from a commercially available AUV.

The results show that the simulation model captures

the AUV motion at low-speed and compares well with

the experimental data.

The results of the research are promising and sug-

gest that torpedo-shaped AUVs can be effectively

controlled at low-speed with only a few thrusters. The

next step in our work is to construct modules for the

testbed AUV which contain thrusters within them. In-

corporate these modules into the AUV and repeat the

experimental testing. In the future, we will consider

what type of thrusters are most suitable, i.e., the typi-

cal propeller thrusters, or more novel devices, such as

vortex ring generators or pulsating membranes.

ACKNOWLEDGEMENTS

We would like to thank the University of Iceland for

lending us their Gavia AUV to perform the experi-

ments. We would also like to acknowledge the staff

at Teledyne Gavia ehf. for their assistance during this

work.

REFERENCES

Allen, B., Vorus, W., and Prestero, T. (2000). Propulsion

system performance enhancements on remus auvs. In

OCEANS 2000 MTS/IEEE Conference and Exhibi-

tion, volume 3, pages 1869–1873. IEEE.

Ananthakrishnan, P. and Decron, S. (2000). Dynamic sta-

bility of small and mini-autonomous underwater vehi-

cles: Part i. analysis and simulation for mid water ap-

plications. Technical report, Technical Report, Florida

Atlantic University, Florida.

Braunl, T., Boeing, A., Gonzalez, L., Koestler, A., and

Nguyen, M. (2007). Design, modelling and simulation

of an autonomous underwater vehicle. International

Journal of Vehicle Autonomous Systems, 4, 2(3):106–

121.

Clark, T., Klein, P., Lake, G., Lawrence-Simon, S., Moore,

J., Rhea-Carver, B., Sotola, M., Wilson, S., Wolf-

skill, C., and Wu, A. (2009). Kraken: Kinematically

roving autonomously kontrolled electro-nautic. 47th

AIAA Aerospace Sciences Meeting Including the New

Horizons Forum and Aerospace Exposition, Orlando,

Florida.

de Barros, E., Dantas, J., Pascoal, A., and de S

a, E.

(2008). Investigation of normal force and moment co-

efﬁcients for an auv at nonlinear angle of attack and

sideslip range. IEEE Journal of Oceanic Engineering,

33(4):538–549.

Eastman, D., Lambrechts, P., and Turevskiy, A. (2009). De-

sign and veriﬁcation of motion control algorithms us-

ing simulation. Embedded Systems Conference, pages

1–4.

Fossen, T. (1994). Guidance and Control of Ocean Vehicles.

John Wiley & Sons.

Helgason, B. (2012). Low speed modeling and simulation

of gavia auv. Master’s thesis, Reykjavik University.

Kennedy, J. (2002). Decoupled modelling and controller de-

sign for the hybrid autonomous underwater vehicles:

Maco. Master’s thesis, Univeristy of Victoria.

Mathworks (2011). Simulink/Matlab.

Wang, W. and Clark, C. (2007). Modeling and simulation

of the Videoray Pro III underwater vehicle. OCEANS

2006-Asia Paciﬁc, pages 1–7.

White, F. M. (2008). Fluid Mechanics. McGraw-Hill, 6

edition.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

338