Modeling and Visualizing Individual and Global Trends of a Multi-agent

System

Vinicius Nonnenmacher, Marta Becker Villamil and Luiz Paulo Luna de Oliveira

Applied Computing-Graduate Program, Universidade do Vale do Rio dos Sinos,

Av. Unisinos 950, S

ao Leopoldo, Brazil

Keywords:

Simulation, Social groups.

Abstract:

This paper proposes a new model for real-time visualization of the social dynamics as a resultant of individual

changes due to their mutual interactions. The model allows the dynamical visualization of both, the individual

characteristics changes as well as the resultant system trends as a whole. As an application, we investigated the

role of individual degrees of inﬂuence and the number of agents in the global choice of a population between

two antagonistic options.

1 INTRODUCTION

Recently mathematical models have gained ground

in the simulation of biological and sociological be-

havioral phenomena. In some ﬁelds of science these

models have helped to understand the operation of

other complex systems, such as the transmission of

disease or the tendency of an economic system.

One of the subject of sociological research is so-

cial behavior, or collective action. The collective be-

havior modeling is the result of actions, decisions,

or thinking of individual social actors (agents) that

lead to diffusion of innovations, coordination of con-

ventions, emergent norms, and cultural convergence.

At the emergent structure of these kind of models,

agents change location or behavior in response to so-

cial inﬂuences . Rather than producing homogene-

ity these decisions aggregate to produce global pat-

terns of cultural differentiation, stratiﬁcation, and ho-

mophilic clustering in local networks

(Macy and

Willer, 2002) One limitation in most social inﬂuence

models is the assumption that inﬂuence is only posi-

tive. However, social relations can also have negative

valence, such that the state of an agent tends toward

maximal distinctiveness rather than similarity.

Theory of information and social structure has the

basic insight that the amount of widely shared infor-

mation in a system is negatively related to the level

of social differentiation in that system (Mark, 1998).

Homophily: the tendency to interact more frequently

with similar agents

In other words, high levels of shared information and

high levels of social differentiation do not occur in

the same societies at the same times. Social inﬂuence

occurs when an individual’s thoughts, feelings or ac-

tions are affected by other people. Social inﬂuence

takes many forms and can be seen in conformity, so-

cialization, peer pressure, obedience, leadership, per-

suasion, sales, and marketing.

Morton Deutsch and Harold Gerard (Deutsch and

Gerard, 1955) described two psychological needs that

lead humans to conform to the expectations of others.

These include our need to be right (informational so-

cial inﬂuence), and our need to be liked (normative

social inﬂuence). The informational social inﬂuence

is prominent in ambiguous social situations where

people are unable to determine the appropriate mode

of behavior, and is driven by the assumption that sur-

rounding people possess more knowledge about the

situation. Normative social inﬂuence is ”the inﬂuence

of other people that leads us to conform in order to

be liked and accepted by them.” In many cases, nor-

mative social inﬂuence serves to promote social co-

hesion. When a majority of group members conform

to social norms, the group generally becomes more

stable.

A multi-agent system (MAS) has multiple in-

teracting intelligent agents. They present self-

organization and related complex behaviors based on

agents simple parameters. They have been applied

in the real world to graphical applications such as

computer games and movies. Other applications in-

clude transportation, economy, networking and mo-

339

Nonnenmacher V., Becker Villamil M. and Luna de Oliveira L..

Modeling and Visualizing Individual and Global Trends of a Multi-agent System.

DOI: 10.5220/0004047903390344

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 339-344

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

bile technologies. Usually we can visualize over sim-

ulation time only the result or emergence of these sys-

tems at the macroscopic way. The real-time visualiza-

tion of agents internal parameters is necessary as we

need to change some parameters at few agents to an-

alyze the system perturbation that this carries.

This work proposes a new model that allows the

analysis of a multi-agent system in order to investi-

gate which parameter is decisive to one society de-

cides to choose between two different concurrent con-

cepts. A real time visualization of the individual in-

ternal parameters allows researcher to identify the in-

dividual and global tendencies of the role system.

The outline of this paper is as follows: after pre-

senting the related work in the next section, we will

present our social model with some explanation about

the agents parameters and their interactions. After

that, a section explaining the two kinds of MAS visu-

alization. Some results of the simulation is explained

at Section and a conclusion will be given in the last

section of this paper.

2 RELATED WORK

Computer Graphics area has been extensively work-

ing with complexity of MASs systems. Works like

the modeling of ﬂock of birds(Reynolds, 1987)and

(Resnick, 1994) was the forerunners of the recent

works like (Vigueras et al., 2010), (Narain et al.,

2009) . For modeling the ﬂock, instead to use a

bottom up approach based on agent-level interaction,

Reynolds was able to produce highly realistic ﬂight

formations using very simple rules that imposed rel-

atively small computational demands. He did not

model the ﬂock, nor did he model isolated birds.

He modeled their interaction, at the relational level.

Agent-based models of human social interaction are

based on this same theory-building strategy. Like

ﬂocks of birds, recently simulations of human crowds

processes are highly complex, non- linear, path de-

pendent, and self-organizing (Ondrej et al., 2010);

(Guy et al., 2010); (Prazak et al., 2009). We may be

able to understand these dynamics much better not by

trying to model them at the global level but instead as

emergent properties of local interaction among adap-

tive agents who inﬂuence one another in response

to the inﬂuence they receive . Simulation of soci-

eties as complex non-linear systems, which are dif-

ﬁcult to study with classical mathematical equation-

based models has been used to simulate agent inter-

action with applications ranging from economy, bi-

ology and sociology areas (Helbing, 2009; Newman,

2003). Usually, groups modelling through interac-

Figure 1: Simulation scene. The agents move around and

interact.

tions is aplicated to crowd behavior simulation, Qiu et

al. (Qiu and Hu, 2010) presenedt in their work a unied

and well-dened framework for modeling the structure

aspect of different groups in pedestriancrowds. Both

intra-group structure and inter-group relationships are

considered and their effects on the crowd behavior are

modeled. As result it was presented that different

group sizes, intra- group structures and inter-group

relationships can have signicant impacts on crowd be-

haviors Villamil et al. (Villamil et al., 2005) presented

a work to simulate social groups formation and inter-

action based on simple rules and agents progression.

The competitive behaviors of those groups in the con-

text of behavioral animation was also simulated. As

the work presented here, psychological and physio-

logical characteristics of group and its effect on trafﬁc

characteristics (speed, inter-distance, array of group)

was not analyzed. As Villamil et al. work, this ar-

ticle also present a simulation with sociological con-

notation. But, in this case, we are not interested in

groups displacement in a scene. Inﬂuence area, for

example, do not has the same meaning in terms of

local distance inside the scene where one agent can

inﬂuence other. It can be considered an analogy to

the level of inﬂuence of person on a big population

through television. In this case, the simulation pre-

sented here differs from crowd simulation because it

does not consider personal distance as a preponderant

factor to interaction.

3 INDIVIDUAL COMPETITIVE

MODEL

Simulation is based on a system where agents graphi-

cally represented by a cube get around a scenario ran-

domly. At the beginning agents are positioned ran-

domly and move continuously changing their routs

during the simulation (Figure1).

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

340

3.1 Agents Parameters

Each agent has social individual characteristics de-

scribed as follows:

• Inﬂuence (I). The capacity or power of persons

or things to be a compelling force on producing

effects on the actions, behavior, opinions of the

others was modeled in terms of magnitude. In-

ﬂuence is based on popularity (either directly or

indirectly) or success or some combination of the

two and is not only related to a direct interac-

tion. It was represented by a bounding hemisphere

around the cube. The circle area that forms the

base of the hemisphere is directly proportional to

the inﬂuence of the agent. So, the most inﬂuent

agent of simulation has its hemisphere with a di-

ameter equal to the scenario width. Inﬂuence pa-

rameter has threshold between 0 and 1.

• Communicability (v). Agents communicability

represents the speed of exchange of thoughts,

messages, or information, using some way such

as speech, signals, writing, or behavior. In our

model, the communicability of each agent is rep-

resented by its velocity, with which it run about

the simulation space. The number of interactions

involving a speciﬁc agent is proportional to its

velocity. Communicability parameter also has a

threshold between 0 and 1.

• Status (S). Accounts for the position, or opinion,

of each agent with respect to two concurrent or an-

tagonistic concepts (products, teams, ideas, etc.)

In our model, 1 ≤ S

≤ −1, for each agent i, where

larger proximity to the extremes indicates greater

conviction for one or other concurrent concepts.

A threshold 0 < S

< 1 of this parameter divides

the set of agents in three groups:

= {A

; S

≤ S

≤ 1} (1)

= {A

; −S

< S

} (2)

−

= {A

; −1 ≤ S

≤ −S

} (3)

In this paper, S

= 0.5, in such a way that G

empty.

3.2 Agents Interaction

Agents inﬂuence each other in response to the in-

ﬂuence they receive. One agent can inﬂuence other

when the other is inside its bounding hemisphere. In-

ﬂuence level (I) can be modiﬁed at each interaction as

shown in Equations (4) for i-agent and (5) for j-agent.

Modeling interaction between two agents is not a sim-

ple task. Moreover, there are an enormous variety

of ways those interactions can take place. Here, we

adopt the simplest possible premisses to attain math-

ematical expressions for those relations. We expected

that, even being simple, such a model can express

the most basic characteristics of social interactions.

In what follows, we present the formulation of our

model with respect to the change of our basic vari-

ables (I, v and S) when two agent A

and A

interact

with each other.

For inﬂuence, we suppose that the change of inﬂu-

ence of agent A

is proportional to the inﬂuence of A

being positive when both agents have the same direc-

tions of opinion (S

and S

with the same signs), and

negative when they have opposite directions of opin-

ion (S

and S

with opposite signs). The adopted pro-

portionality constant is 1/N. The same is supposed

for agent A

. Then, the inﬂuence degree I

n+1

in time

n + 1 after a relation with agent A

is given by

n+1

= I

(4)

n+1

= I

(5)

Adopting a quite similar approach for the other

variables S and v, we have

n+1

= S

(6)

n+1

= S

(7)

n+1

= v

(8)

n+1

= v

(9)

where, after each relation, the direction θ for the ve-

locity actualization is taken randomly in the range

0 ≤ θ < 2π . According to above equations, an inter-

action between two agents belonging to antagonistic

groups is always taken as a destructive interference

for both agents, since it causes a reduction of all three

variables S, v and I. On the other hand, an interaction

with agents of the same group increases these vari-

ables, and are taken always as a constructive interac-

tion. Equations represent the dichotomic characteris-

tic of the model, where agents Status tend to 1 or -1

depending on the inﬂuences they receive over simula-

tion.

The above equations rule the dynamics of the set

of agents, that are put to run with their respective ve-

locities, into a simulation ambient. When a agent A

gets inside a circle of inﬂuence of agent A

(with ra-

dius I

) the variables of A

are actualized according to

ModelingandVisualizingIndividualandGlobalTrendsofaMulti-agentSystem

341

the above equations. As time passes by, transitions of

agents between groups G

and G

−

take place. The

objective of this paper is to study the asymptotic be-

havior of this hypothetical society, to see its ﬁnal equi-

librium state. The possible results includes the victory

of G

−

(with the extinction of G

), the victory of G

(with the extinction of G

−

) , and the coexistence of

both G

and G

−

For a better understanding of the system trends we

developed two kinds of real-time visualization: one

concerning the total agents displacement (Window 1),

their interactions, and their inﬂuence area and its vari-

ation in a scenario (Figure1).

The other one is related to individual internal pa-

rameters (Window 2) (Figure2). Usually, simulations

involving MASs are analyzing by changing initial pa-

rameters and observing the trends of the system as a

role. In this case, changes of individual parameters

during simulation are not possible to identiﬁed in real

time.

To analyze agents dynamical internal parameters,

each agent is represented by a sphere positioned at

RGB color space. The individual parameters, Inﬂu-

ence (I), Communicability (v), Status (S), is repre-

sented by chromaticities of the red, green, and blue

additive primaries, and can produce at real-time any

chromaticity that is the triangle deﬁned by those pri-

mary colors. Normalized values of these parame-

ters were changed to ﬁt on the corespondent values

of RGB. Inﬂuence was deﬁned on the red threshold

chromaticitie, Communicability was deﬁned on the

green and Status was deﬁned on blue. Spheres change

their color and position during simulation as agents

parameters change. Figure 2 shows a simulation time-

step where all agents parameters are uniformly dis-

tributed on the RGB color space.

Moreover, system user can select some agent by a

mouse clic at the visualization Window 1 and observe

its position and internal parameters trends at visual-

ization Window 2. This is the ﬁrst step to predict the

future behavior of the system based on present. As we

know, simulation models like this, tend to grow large

in size and complexity, and may be difﬁcult to under-

stand which is the cause of system result. For exam-

ple, only one agent with large inﬂuence can modiﬁed

throw interactions all other agents parameters very

quickly. And, in this way, we can ask us: what would

happen with the role system if we decrease only this

agent parameter during the simulation? And, on the

other hand, if we choose a group of agents and in-

crease Inﬂuence parameter, or their Communicabil-

ity? Would it be sufﬁcient to reverse the big inﬂuence

of this agent?

Figure 2: Visualization window 2. At this point of sim-

ulation there is much more agents with parameter S < 0.

Communicability (v) seems to be uniformly distributed.

4 RESULTS AND DISCUSSION

In this section, we present computational experiments

to get conclusions under two mains aspects: asymp-

totic behavior and the role of extremism over the

asymptotic results.

4.1 The Role of Inﬂuence I

Although simulation designs were used experimen-

tal rather than post- hoc statistical controls to iden-

tify underlying causal processes, statistical of the re-

sults were also done to system analysis. ABMs re-

quire replications that demonstrate the stability of the

results. Replications include variation in parameters

that are theoretically arbitrary or of secondary inter-

est. Agents S parameter means its position with re-

spect to two concurrent antagonistic concepts that can

be a product, teams, ideas or political parties. S limits

are -1 and . The closer these limits, the more con-

vinced about the concept becomes the agent. As re-

sult it was analyzed the impact of Inﬂuence parameter

to the agents choices. How the agents choices change

based on their interactions with others more inﬂuents?

The ﬁrst result is related to system convergence. If

the number of inﬂuent agents is big, faster all agents

choose a side convinced. To investigate this, v and

I parameters were lock as they initiate. It was per-

formed 10 simulations for different I parameter aver-

ages. Initial Is were distributed with a 0.2 average and

with a standard deviation of 0.1 meaning not inﬂuent

agents. Also it was done more two set of simulations

with Is distributed with a 0.5 average (medium inﬂu-

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

342

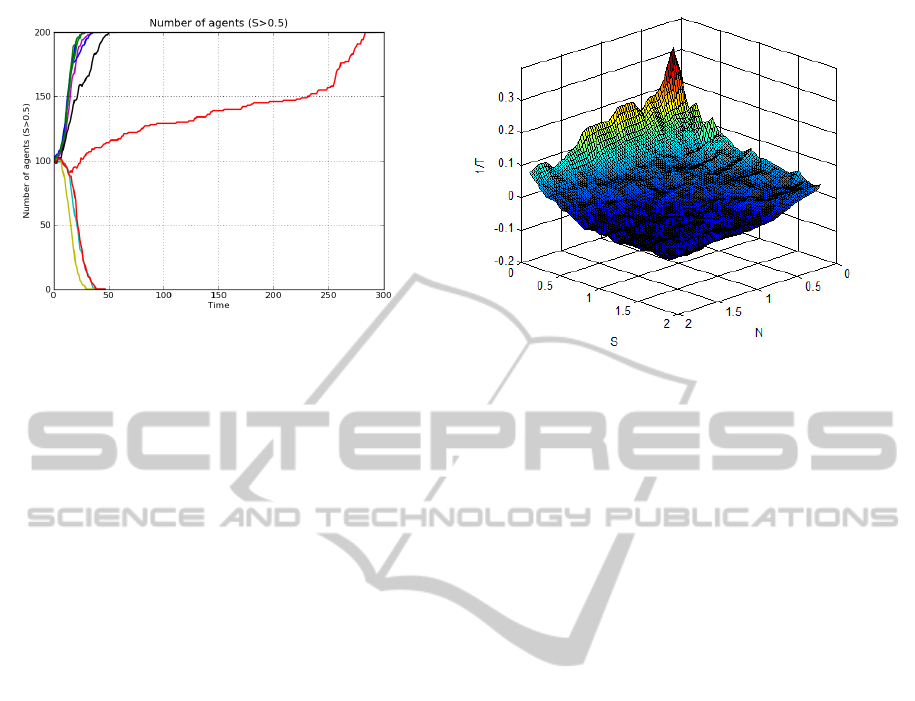
Figure 3: Agents parameter I with an average of 0.7.

ent agents) and Is distributed with a 0.7 average (in-

ﬂuent agents). The standard deviation was maintained

at 0.1 for all simulations. We can observe that sim-

ulations that has agents more inﬂuents like the ones

at Figure 3 converge much quickly (9 simulation of

10 converges before frame 50) . And, on the other

side, simulations with not inﬂuents agents converges

slowly and agents change their Ss much times.

4.2 The Role of Extremism

Extremism denotes how close, in average, a group is

to on of the extrems = 1 or −1. To this investigation,

more than 400 simulations where made, with group

−

conﬁgured as in the previous Section, only vary-

ing the number of agents N as well as the extremism S

of one group in relation to the other. In this section we

will denote N = N

−

and S = S

−

. We consid-

ered 20 values for each of these parameters and made

the 400 corresponding simulations. With that we ob-

tain a 20x20 grid where the maximum and minimum

value for two axis are 2 and 0 respectively. Each point

in the grid is a relation beween the parameters of G

and G

−

). For example, the central point( 1,

1 ) of the grid is the equal distribution of parameters,

where the number of agents is 100 and the extremism

is 0.5 for both groups. To score the results, we mea-

sure T (N,S) = V /t, where t is the convergence time

of the corresponding simulations. To differ between

the victory of G

from the victory of G

−

, we make

V = 1 and V = −1, respectively.

As the result we have a surface that displays the

behavior of the system for different values of num-

ber of agents an extremism considering two opposite

groups. From that surface we can see that group G

wins for smaller values of S and greater values of N,

while the opposite occurs for the cases of victories of

−

. Moreover, some region of draws occurs between.

The overall result is easier to see from the curve lev-

Figure 4: Function T(N,S), as a function of N e S.

els, showed in (Figure 4). There we can see the curve

T (N,S = 0) passing by the point (1, 1) as a conﬁrma-

tion that, when G

and G

−

have the same values for

N and S simultaneously, the convergence time tends

to inﬁnite (draw). In the same ﬁgure, others curve

levels can be seen, for positive and negative values of

T (N,S). Another conclusion we can take is about the

minimum value that the relations for a equilibrium or

a negative convergence (G

). Its possible to note that

the the minimum relation value for a negative conver-

gence is the same for number of agents N = 1 and S:

0.6. In other words, adding N and S in the same pro-

portion causes the same effect in convergence time

and pole. Other data that must be explained is the

quantity of levels in the positive z value side of the

surface. That is because in lower relation values G1

is very less competitive than G

−

causing a very low

time positive conversion, and in the negative z value

side, G1 even being superior in values, is competing

with a medium group, of medium variables. We con-

sider so far this data irrelevant. We can conclude that

the N and S has the same weight in two competing

groups scenario. Thats because the minimum rela-

tions nedded for G1 to converge is the same.

5 CONCLUSIONS

In this paper, we introduced a new model for visual-

izing dynamics of social evolution in real time. It is

applicable to any set of interacting individuals which

is modeled as a multi-agent system, as the one pro-

posed here as an example. Moreover, it permits to

follow individual evolution of speciﬁc agents selected

while the simulation is running (by user interaction).

The social model for social evolution of interact-

ing agents proposed here and used as an example of

ModelingandVisualizingIndividualandGlobalTrendsofaMulti-agentSystem

343

Figure 5: Surface that represents the behavior of the system

for diferent parameters of N and S.

application of the visualization model is based on very

simple assumptions. In fact, all the interactions are

based on proportionality of the considered types of

interacting parameters. This makes some of the re-

sults of a social evolution quite predictable in terms

of common cense most of humans have in terms of

society behavior. The application of the visualization

method to such case showed consistent results accord-

ing to those common cense, which gives validation to

the proposed method inside the scope of the consid-

ered case.

As a future work, the visualization model shall

permit to interfere on the evolution of a MAS in real-

time by the possibility of modiﬁcation of individual

parameters to interfere on the system’s fate before

the asymptotic state is achieved. We intend to im-

prove the user interaction to permit select an agent

or a group of agents and change their parameters dur-

ing simulation and analyze how the system as a whole

would react. In this way, we could know what agents

or groups of agents are crucial to desired certain con-

vergence of the system. We also are working to im-

prove S parameter to consider it as a n-dimensional

vector to make it possible to include other agents char-

acteristics and choi ces related to its gender, work,

hobbies, etc.

REFERENCES

Deutsch, M. and Gerard, H. B. (1955). A study of norma-

tive and informational social inﬂuences upon individ-

ual judgment. The Journal of Abnormal and Social

Psychology, 51:629–636.

Guy, S. J., Chhugani, J., Curtis, S., Dubey, P., Lin, M., and

Manocha, D. (2010). Pledestrians: a least-effort ap-

proach to crowd simulation. In Proceedings of the

2010 ACM SIGGRAPH/Eurographics Symposium on

Computer Animation, SCA ’10, pages 119–128, Aire-

la-Ville, Switzerland, Switzerland. Eurographics As-

sociation.

Helbing, D. (2009). Managing complexity in socio-

economic systems. European Review, 17:423–438.

Macy, M. W. and Willer, R. (2002). From factors to actors:

Computational sociology and agent-based modeling.

Annual Review of Sociology, 28:143–166.

Mark, N. (1998). Beyond individual differences: Social

differentiation from ﬁrst principles. American Socio-

logical Review, 63(3):pp. 309–330.

Narain, R., Golas, A., Curtis, S., and Lin, M. C. (2009). Ag-

gregate dynamics for dense crowd simulation. ACM

Trans. Graph., 28:122:1–122:8.

Newman, M. E. J. (2003). The structure and function of

complex networks. SIAM REVIEW, 45:167–256.

Ondrej, J., Pettre, J., Olivier, A.-H., and Donikian, S.

(2010). A synthetic-vision-based steering approach

for crowd simulation. SIGGRAPH ’10: ACM SIG-

GRAPH 2010 Papers.

Prazak, M., Kavan, L., McDonnell, R., Dobbyn, S., and

O’Sullivan, C. (2009). Moving crowds: a linear ani-

mation system for crowd simulation. In Proceedings

of the 2009 symposium on Interactive 3D graphics and

games, I3D ’09, pages 9:1–9:1, New York, NY, USA.

ACM.

Qiu, F. and Hu, X. (2010). Modeling group structures in

pedestrian crowd simulation. Simulation Modelling

Practice and Theory, 18(2):190 – 205.

Resnick, M. (1994). Turtles, termites, and trafﬁc jams: ex-

plorations in massively parallel microworlds. MIT

Press, Cambridge, MA, USA.

Reynolds, C. W. (1987). Flocks, herds and schools: A

distributed behavioral model. SIGGRAPH Comput.

Graph., 21(4):25–34.

Vigueras, G., Lozano, M., Ordu

na, J. M., and Grimaldo,

F. (2010). A comparative study of partitioning meth-

ods for crowd simulations. Appl. Soft Comput.,

10(1):225–235.

Villamil, M. B., Oliveira, L. P. L., and Musse, S. R. (2005).

A model for generating competitive groups based on

virtual agents progression. In International Con-

ference on Computer Animation and Social Agents,

pages 133–138. Hong Kong Polytechnic University.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

344