
A Fast, Efficient Multi-Direct Forcing of Immersed Boundary
Method for Flow in Complex Geometry
Anyang Wei, Hui Zhao, Jin Jun and Jianren Fan
State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou, P.R. China
Keywords: Immersed Boundary Method, Efficient, Fast, Multi-Direct Forcing.
Abstract: The Immersed Boundary method (IBM) has received wide attention from last decade, due to its promising
application to solve the fluid-solid interaction problems in large quantities of practical engineering areas.
This paper implemented IBM with Multi-Direct-Forcing (MDF), presenting the evaluation of momentum
forces on the body surface - interaction forces between fluid-solid. Grounded on the Multi-Direct-Forcing
method, we constructed a new system that could be efficiently and fast solved. Meanwhile, this proposed
algorithm is easy to code and implement parallelization. Besides, it can be extended to three-dimensional
simulation without much more extra efforts. Accuracy of the proposed MDF immersed boundary method
has been investigated, as well as some applications such as flow past the cylinder at a set of low Reynolds
numbers.
1 INTRODUCTION
The incompressible fluid flows involving complex
boundaries, which may be stationary or in motion,
are of practical and academic importance. These
problems can be solved by the traditional body-fitted
numerical methods, in which governing equations
are discretized in a curvilinear coordinate system
that conforms to the boundaries, with re-meshing at
each time step. This procedure is not trivial and the
re-mesh computation is heavily cost. To solve the
complex geometrical fluid-interaction problem,
Peskin (Peskin 1972) proposed the Immersed
Boundary method in 1972, when he studied the flow
in heart valves based on the Cartesian grid. With
many structure grid properties retained, this method
gave the complex geometrical fluid-interaction prob-
lems an effective solution direction.
In the past two decades, we have seen the boom of
the Immersed Boundary Method. Several variants of
Immersed Boundary Method have appeared, like
Immersed Interface Method (Peskin 1972; Leveque
and Li 1994), Direct-Forcing Method (Uhlmann
2005) et al.. But all these methods, as the original
method proposed by Peskin, need an interpolation
between the immersed boundary Lagrangian and
Eulerian grid points. When this process is applied to
simple geometries or multiphase flows with a small
amount of particles, it is quantified. However, when
it comes to large quantities of particles or practical
geometries, it also costs a lot, though it is much
easier to implement than body-fitted numerical
method. These days, Ceniceros and Fisher
(Ceniceros and Fisher 2011) have applied the
treecode combined with FMM (Fast March Method)
to simulate large systems, but this method is not
trivial to implement. Wu and Shu et al.(Wu and Shu
2010) directly performed the fluid-interaction force,
deriving a linear system with the immersed bounda-
ry force density as variables. They deemed it was
easy to implement, but they only test two-
dimensional problems, however when it comes
across the three-dimensional systems or large quan-
tities of particles in multiphase flow simulation, that
linear system would be very huge, and the above
metioned FMM and treecode can be a good candi-
date.
Grounded on the work of Luo et al. (Luo, Wang
et al. 2007), Wu and Shu (Wu and Shu 2010), we
proposed another efficient fast immersed boundary
method based on the multi-direct-forcing immersed
boundary method. This paper is organized as fol-
lows. In section 2, firstly the governing equations for
the incompressible Navier–Stokes equations are
presented. Then immersed boundary method imple-
mented with multi-direct-forcing will be briefly
described. At the end of this section, we will propose
309
Wei A., Zhao H., Jun J. and Fan J..
A Fast, Efficient Multi-Direct Forcing of Immersed Boundary Method for Flow in Complex Geometry.
DOI: 10.5220/0004049303090314
In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),
pages 309-314
ISBN: 978-989-8565-20-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

a fast and efficient algorithm based on above de-
scription. Several benchmark cases are simulated for
predicting the accuracy of the proposed MDF Im-
mersed Boundary method in Section 3. Finally, in
section 4, some concluding remarks will be drawn.
2 MATHEMATICS DESCRIPTION
2.1 Governing Equations of Fluid
The dimensionless governing equations for incom-
pressible flows in the computational domain
are:
2
0
1
P
t Re
u
x
u
u u u f
,
(1)
where
u
is the velocity of fluid;
P
is the pressure
and
Re
is Reynolds number;
f
is the force density
of fluid-structure interaction. According to Luo et
al.(Luo, Wang et al. 2007) and Uhlmann (Uhlmann
2005), in multi-direct forcing method of IBM, the
force density
f
is calculated as
( ) ( ) ( )F d ,
f x X x X X
(2)
where
x
is the Eulerian coordinate; e.g. for two di-
mensional problems,
12
=( , ) ( 1 )
i i i
x x i , ,Nx
, where
N
is the number of Eulerian points. And the index
of coordinates are mapped into one-dimensional
index space from two dimensional computational
space for convenient as Wu & Shu (Wu and Shu
2010).
X
,
F
are Lagrangian coordinate and forcing
density on Lagrangian points, respectively. For two
dimensional problems, they can be denoted as
12
()
j j j
X ,XX
and
12
j j j
FF( , )F
( 1 )j , M
,
where
M
is the total number of Lagrangian points.
()
xX
is Dirac delta function.
2.2 Scheme of Multi-Direct-Forcing
In order to satisfy no-slip condition near the bounda-
ry, Lagrangian points coinciding with the boundary,
must be specified with a force
j
F
so as to the veloci-
ties at these points can be equal to velocities at
boundary. In the MDF method, the force can be
determined from Eq.(3)
2
1
P,
t Re t
uu
f u u u rhs
(3)
For the Lagrangian and Eulerian points, one can get
Eq.(4) and Eq.(5) respectively, according to Eq.(3),
1
1
( ) ( )
= ( ),
nn
jj
j j j
nn
j j j j
j
t
ˆ ˆ
tt
UU
F X rhs X
U U U U
rhs X
(4)
( ) ( )
( ),
n 1 n
ii
i i i
n 1 n
i i i i
i
t
ˆ ˆ
tt
uu
f x rhs x
u u u u
rhs x
(5)
where
i
ˆ
u
and
j
ˆ
U
are provisional velocities making the
second term zero.
()
( )=
d
j j j
jj
ˆ
.
t
U U X
FX
(6)
The desired velocity is assumed that it can be
specified by known values, namely,
1
( )=
nd
j j j
U
UX
at
the boundary. Therefore, Eq.(4) can be reduced to
Eq.(6).
According to Uhlmann(Uhlmann 2005) and Wang
et al.(Wang, Fan et al. 2008), it is common to inter-
polate velocities from Eulerian points to Lagrangian
points with Dirac delta Function. There, this process
is directly written in the integral form; however, here,
we try to construct a fast algorithm, hence denote the
interpolation process as an operator A, namely,
12
1
( - )d d
M N N
ˆ ˆ
.
A u u x X x x
(7)
According to Eq.(7), we can get
ˆ
ˆ
Au U
. Then
force density on the immersed boundary
()
jj
FX
can
be directly evaluated. Once this force is calculated,
we can obtain the force density of Eulerian grid
points from the spreading process of
()
jj
FX
, that is
interpolating force on the immersed boundary back
to Eulerian grid.
As the same, we denote this spreading process as
an operator
NM
H
. So we have
N M M 1
.
f H F
(8)
Finally, we can get the velocities at the new time
step, namely
n1
ˆ
t.
u u f
(9)
However, after completing these two processes,
we may find actually the latest fluid field is not
completely satisfying the no-slip condition near the
immersed boundary, therefore MDF with the latest
fluid field redo the above two processes until the no-
slip boundary condition is achieved iteratively,
which is expressed in mathematical form as follows:
k 1 k k
t.
u u f
(10)
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
310

2.3 Fast Algorithm
In the work of Luo et al.(Luo, Wang et al. 2007), at
least twenty iterations are needed to achieve the no-
slip boundary condition. When it comes to solve the
large complex geometries or a number of particles in
fully resolved direct numerical simulation, algo-
rithms with twenty iterations are too cost. Here,
based on the previous work, we take a forward step
to obtain the no-slip boundary condition with much
less iterations.
So, we write the expansion of Eq.(10), and then it
gives
k 1 k k
k d k
t
.
u u HF
u HU HAu
(11)
From the above equation, it is not difficult to ob-
serve that as the iteration continues until
k 1 k
uu
,
the solution of this system converges. That means
0.
dk
HU HAu
(12)
Since
d
U
is known, the problem can be converted
into solving a linear system of
u
satisfying the
Eq.(12). To solve the above system, we need to
analyse the characteristics of the coefficient matrix
HA
(denoting as
Q
), so we can write down the
entries of this matrix
kM
ij ik kj
k1
q h a .
(13)
ik
h
denotes the kth Lagrangian point spreading to the
ith Eulerian grid point;
kj
a
denotes the jth Eulerian
point interpolating to kth Lagrangian point. Due to
the summation over all the Lagrangian points, so we
have
ij ji
qq
, this matrix is symmetrical, positive,
sparse, with many zero entries due to the cut off
effect of Dirac delta function. Here we apply the
steepest descent method to solve this system.
Here we define
k
r
as the residual of kth iteration of
system (12)
k k d
.r HAu HU
(14)
With we only need to evaluate the above defined
residual and an extra multiplication of matrix
Q
with
vector
k
u
as well
kk
k1
kk
,
t.
,
rr
r Qr
(15)
Finally, we can get the iteration formula as fol-
lows:
( ).
k 1 k k d
k1
t
u u HAu HU
(16)
3 NUMERICAL VALIDATION
To validate the accuracy of the algorithm proposed
above, we take the Taylor-Green vortices problem as
validation, which has an analytical solution. Then
uniform cross flows passed a single cylinder with
different Reynolds number are simulated. Drag coef-
ficients, lift coefficients and the Strouhal number of
vortex shedding are compared with previous results.
3.1 Taylor-Green Vortices
In order to validate the modified multi-direct-forcing
of Immersed Boundary method, two-dimensional
decaying vortices with analytical solution is studied.
Computational domain
[-1.5,1.5] [-1.5,1.5]
with a radius unity circular embedded in it is simu-
lated. The flow parameter
Re
equals 100, the time
step
t
as Uhlmann (Uhlmann 2005) is 0.001, grid
size
h
is 1/64. The initial fluid fields and the bound-
ary conditions are both given according to the ana-
lytical solution. The numerical details of fluid solver
can be referred to Wang et al.(Wang, Fan et al.
2008).
The
2,uv
L
norm (Luo, Wang et al. 2007) is defined
as Eq.(17), where (
d
u
,
d
v
)is the desired veloci-
ties,and (
k
u
,
k
v
) is evaluated velocities on the kth
Lagrangian point,
[( - ) +( - ) ]
Np
k d 2 k d 2
k1
2,uv
u u v v
L.
N
(17)
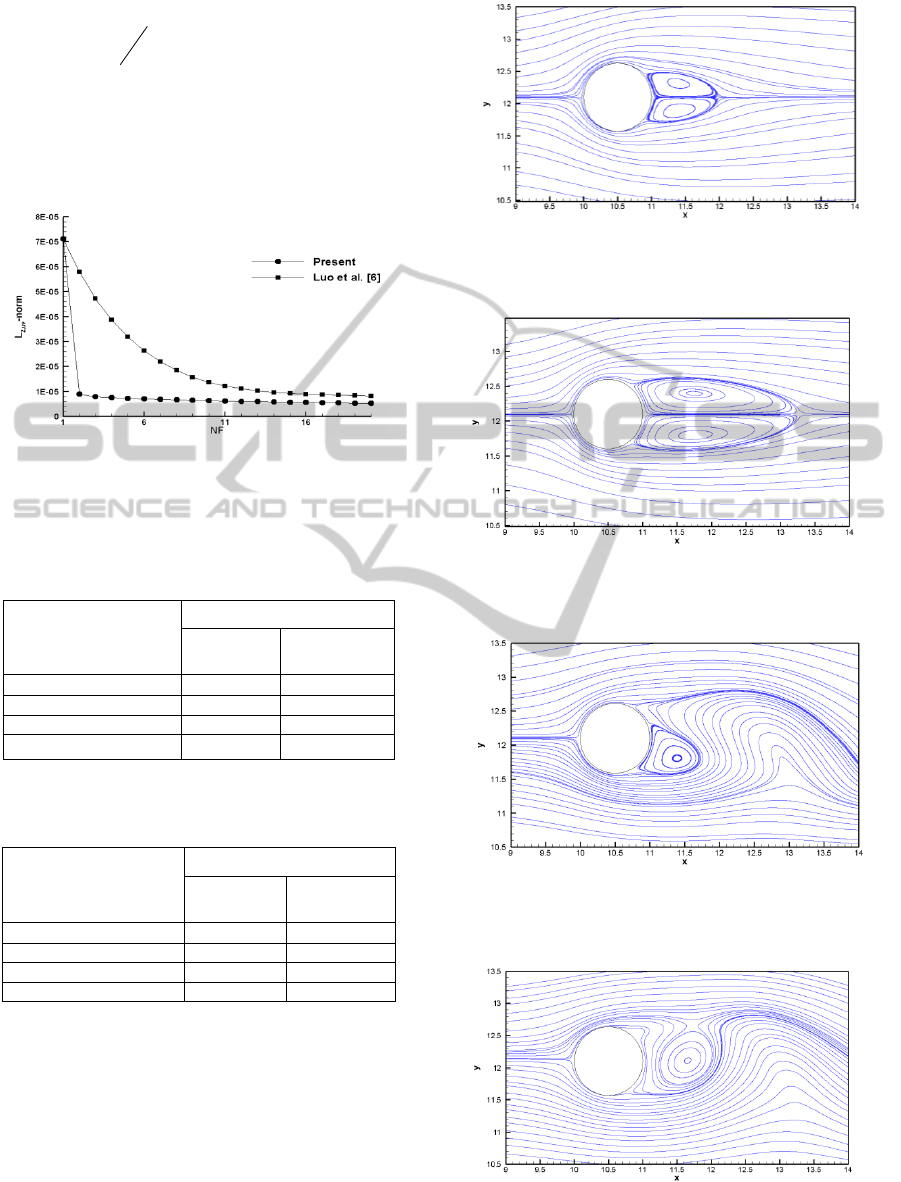
Figure 1 shows the fast convergence of present
modified multi-direct-forcing compared with the
previous Luo et al.(Luo, Wang et al. 2007), only
several iterations are needed to achieve the high
accuracy, which is much less than previous one.
Based on this, we choose to iterate 5 times for the all
latter simulation as default.
3.2 Flow Past Over a Cylinder
Flows past over a circular cylinder has been exten-
sively studied for verifying the algorithms of Im-
mersed Boundary Method. In this study, we place a
cylinder with diameter
0.6D
at the location
(10.5D, 12.1D) in the domain
[0,35D] [0,24D]
.
At the inflow, we give a uniform free-stream veloci-
ty
u
= (1, 0); at the
x= 24D
, we apply the convec-
tive out flow condition as Uhlmann (Uhlmann
2005). The ratio of
A Fast, Efficient Multi-Direct Forcing of Immersed Boundary Method for Flow in Complex Geometry
311
cylinder diameter to grid size is 30, and the Reynolds
number
uD
Re
in our simulation equals to 20,
40, 80, 100, and 200, respectively. And
0.001t
time step is used. Here, in present study, drag and
lift coefficients and Strouhal number will be calcu-
lated for making a comparison with other numerical
and experimental results.
Figure 1: Correlation between the
2,uv
L
norm and the times
of multi-direct-forcing to show the fast convergence as
compared with the previous non-modified algorithm.
Table 1: Comparison of drag coefficient C
D
and recircula-
tion length
w
L
of Re=20.
Authors
Re=20
C
D
w
L
(Tritton 1959)
2.22
(Lima et al. 2003)
2.04
1.04
(Luo, Wang et al. 2007)
2.195
0.97
Present
2.146
0.97
Table 2: Comparison of drag coefficient C
D
and
recirculation length
w
L
of Re=40.
Authors
Re=40
C
D
w
L
(Tritton 1959)
1.48
(Lima et al. 2003)
1.54
2.55
(Luo, Wang et al. 2007)
1.62
2.35
Present
1.567
2.227
From the case
20Re
and
40Re
, it can be seen
from the streamline vector Figure 2 and Figure 3, the
wake behind the cylinder seems to be symmetric and
steady, which are in good agreement with the well-
established results. Table 1 shows that the drag co-
effcients and length of the recirculation zone
w
L
agreeing quite well with published results by
(Tritton 1959; Lima E Silva, Silveira-Neto et al.
2003; Luo, Wang et al., 2007).
Figure 2: The predicted results in the near wake of the
investigated circular cylinder at T = 200, streamline con-
tours, Re = 20.
Figure 3: The predicted results in the near wake of the
investigated circular cylinder at T = 200, streamline con-
tours, Re = 40.
Figure 4: The predicted results in the near wake of the
investigated circular cylinder at T = 200, streamline con-
tours, Re = 100.
Figure 5: The predicted results in the near wake of the
investigated circular cylinder at T = 200, streamline con-
tours, Re = 200.
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
312
The cylinder wake becomes unstable observed as
47Re
. This is indeed what we predict from the
simulation carried out at Re = 100 and 200. Figure 4
and Figure 5 plots the streamline vector T = 200 for
Re = 100 and 200, respectively. As predicted, the
vortex shedding phenomenon is presented; hence the
modified multi-direct-forcing method can predict the
unsteady fluid flow in the complex geometries.
Table 3: Comparison of the predicted drag coefficients, lift
coefficients with other numerical results performed at Re =
100 and 200.
Authors
Re=100
C
D
C
L
(Clift 1978)
1.24
(Stålberg, Bruger et al.
2006)
1.32 ± 0.009
±0.33
(Chiu, Sheu et al. 2008)
1.34 ± 0.011
±0.32
(Calhoun 2002)
1.35 ± 0.014
±0.30
(Chiu, Lin et al. 2010)
1.35 ± 0.012
±0.3
Present
1.3140.009
0.32
Table 4: Comparison of the predicted drag coefficients, lift
coefficients with other numerical results performed at Re =
100 and 200.
Authors
Re=200
C
D
C
L
(Clift 1978)
1.16
(Stålberg, Bruger et al.
2006)
(Chiu, Sheu et al. 2008)
1.36 ± 0.048
±0.64
(Calhoun 2002)
1.17 ± 0.058
±0.67
(Chiu, Lin et al. 2010)
1.37 ± 0.051
±0.71
Present
1.2790.043
0.658
Table 3 and Table 4 give the comparison of the
predicted drag coefficients, lift coefficients of pre-
sent algorithm with other established results in
(Calhoun 2002; Stålberg, Bruger et al. 2006) at Re =
100 and Re = 200. We can find that in our simula-
tion results, the drag coefficient is lower than any
others’, with exception of Stålberg et al.(Stålberg,
Bruger et al. 2006), but it is more closer to the ex-
perimental data of Clift et al. (Clift 1978). The lift
coefficients at these two cases, predict almost the
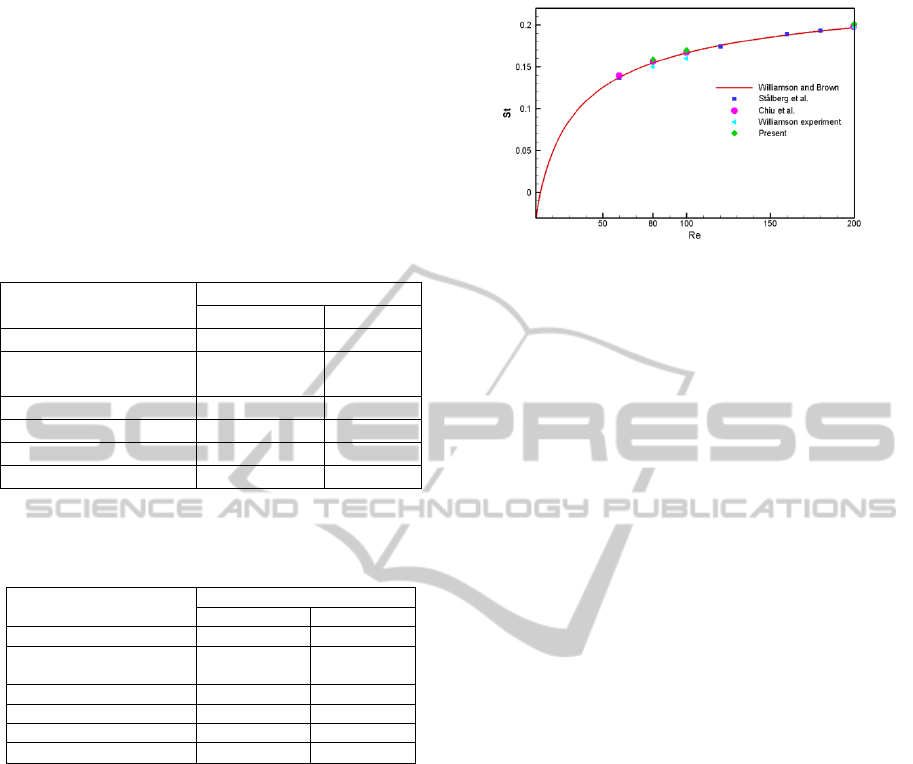
same with others. Meanwhile, we give the relation
of Strouhal number with Reynolds number, and
comparisons are made with the experimental corre-
lation formula and experimental data (Williamson
1996), as well as some other numerical results.
Thereby, the accuracy of present scheme can be
confirmed.
Figure 6: Strouhal number vs. Reynolds number.
4 CONCLUSIONS
In this paper, we proposed a novel fast and efficient
immersed boundary method implemented with mul-
ti-direct-forcing to evaluate the fluid-solid interac-
tions. The accuracy of the proposed multi-direct-
forcing immersed boundary method has been vali-
dated through the several benchmarks with only
several iterations, which are much less than previous
Multi-direct-forcing. However, we only test the two
dimensional applications. When it is applied to
complex three dimensional geometries, theoretically
it would not induce much more extra work, but the
problem whether the matrix calculation in three
dimensional cases will cause the extra cost so that it
induces inefficiency, should need much more care-
fully detailed numerical experiments in the future.
ACKNOWLEDGEMENTS
Financial support from the National Nature Science
of Foundation (No.51136006) of China is gratefully
acknowledged. We also thank Professor Kun Luo
for providing discussion and advice.
REFERENCES
Calhoun, D. (2002). A Cartesian grid method for solving
the two-dimensional streamfunction-vorticity
equations in irregular regions. Journal of
Computational Physics 176(2): 231-275.
Ceniceros, H. D. and J. E. Fisher (2011). A fast, robust,
and non-stiff Immersed Boundary Method. Journal of
Computational Physics 230(12): 5133-5153.
Chiu, P. H., R. K. Lin, et al. (2010). A differentially
interpolated direct forcing immersed boundary method
for predicting incompressible Navier–Stokes equations
A Fast, Efficient Multi-Direct Forcing of Immersed Boundary Method for Flow in Complex Geometry
313

in time-varying complex geometries. Journal of
Computational Physics 229(12): 4476-4500.
Chiu, P. H., T. W. H. Sheu, et al. (2008). An effective
explicit pressure gradient scheme implemented in the
two-level non-staggered grids for incompressible
Navier-Stokes equations. Journal of Computational
Physics 227(8): 4018-4037.
Clift, R., Grace, J., Weber, M. E. (1978). Bubbles, Drops,
and Particles, Academic Press,Inc.London Ltd.
Leveque, R. J. and Z. L. Li (1994). The Immersed
Interface Method For Elliptic-Equations with
Discontinuous Coefficients and Singular Sources.
Siam Journal on Numerical Analysis 31(4): 1019-1044.
Lima E Silva, A. L. F., A. Silveira-Neto, et al., 2003.
Numerical simulation of two-dimensional flows over a
circular cylinder using the immersed boundary method.
Journal of Computational Physics 189(2): 351-370.
Luo, K., Z. Wang, et al. (2007). Full-scale solutions to
particle-laden flows: Multidirect forcing and immersed
boundary method. Physical Review E 76(6): 066709.
Peskin, C. S. (1972). Flow patterns around heart valves -
numerical method. Journal of Computational Physics
10(2): 252-271.
Stålberg, E., A. Bruger, et al. (2006). High order accurate
solution of flow past a circular cylinder. Journal of
Scientific Computing 27(1-3): 431-441.
Tritton, D. J. (1959). Experiments On The Flow Past A
Circular Cylinder At Low Reynolds Numbers. Journal
of Fluid Mechanics 6(4): 547-567.
Uhlmann, M. (2005). An immersed boundary method with
direct forcing for the simulation of particulate flows.
Journal of Computational Physics 209(2): 448-476.
Wang, Z., J. Fan, et al. (2008). Combined multi-direct
forcing and immersed boundary method for simulating
flows with moving particles. International Journal of
Multiphase Flow 34(3): 283-302.
Williamson, C. H. K. (1996). Vortex dynamics in the
cylinder wake. Annual Review Of Fluid Mechanics
28(1): 477-539.
Williamson, C. H. K. and G. L. Brown (1998). A series in
1/√Re to represent the Strouhal–Reynolds number
relationship of the cylinder wake. Journal of Fluids
and Structures 12(8): 1073-1085.
Wu, J. and C. Shu (2010). An improved immersed
boundary-lattice Boltzmann method for simulating
three-dimensional incompressible flows. Journal Of
Computational Physics 229(13): 5022-5042.
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
314
