A Really Simple Explanation of Policy Punctuations?

Interdependence, Complexity, and Policy Punctuations

Florian Prange

and Søren Serritzlew

GORDIS GmbH, Bernstorffstraße 118, 22767 Hamburg, Germany

University of Aarhus, Bartholins Allé 7, 8000 Aarhus C., Denmark

Keywords: Theory of Budgeting, Policy Punctuations, Agent based Modeling, Complexity, Non-Equilibrium Games.

Abstract: We know for a fact that changes in budgets follow a leptokurtic or power law distribution. We have solid

evidence that the degree of leptokurtosis can be explained by factors such as special features of policy areas,

information processing, decision costs, and differences in the institutional setting (Jones & Baumgartner,

2005a; 2005b, Breunig, 2007; Jones, Sulkin and Larsen, 2003; Breunig and Koski, 2006). However, we do

not know why leptokurtosis is omnipresent. In this paper we conjecture that leptokurtosis can be explained

by four simple observations which must be true of any budgeting process: (1) that several actors request and

spend budgets, (2) several actors allocate funding, (3) that actors which do not receive sufficient funding

will eventually close down, and (4) that available funding is limited and often smaller than requested

funding. We first review the literature on policy punctuations and leptokurtosis, and identify the four simple

observations. We then discuss how a simulation can be useful in investigating the implications of these four

observations, and introduce a simulation of the interaction of beggars and philanthropists in a budget game.

We show that the four observations can account for the omnipresence of leptokurtosis at the sub system

level. They cannot, however, explain the magnitude of leptokurtosis found in empirical distributions of

budget changes.

1 COMPLEX PATTERNS WITH A

SIMPLE EXPLANATION IN

THE THEORY OF POLICY

PUNCTUATION

Public budgeting is, in a sense, very well

understood. When Aaron Wildavsky and his

colleagues almost 50 years ago began to use

quantitative methods in the study of public

budgeting, it became clear that public budgets are,

compared to other phenomena within the realm of

political science, extremely easy to predict. Budgets

almost always develop ‘incrementally’, i.e. they tend

to grow slowly and gradually year after year. If one

knows the budget for one year of a country, a

municipality, a public agency, or some other entity,

it is fairly easy to predict next year’s budget. Just

add a small fraction and you have, almost always, a

very good estimate. This has been documented in

several studies, in various ways and countries (see,

for instance, Davis, Dempster & Wildavsky, 1966;

Jones, Baumgartner & True, 1998).

However, this is only one side of the story.

Although public budgets are indeed predictable and

changes small most of the time, once in a while,

often when least expected, changes of catastrophic

nature occur (Padgett 1980; Jones, Baumgartner &

True, 1998). Figure 1 shows the distribution of

budget changes in U.S. budget outlays for almost

200 years. Compared to a normal distribution, it has

a characteristic form. Small changes are very

frequent, and much more frequent than in a normal

distribution with similar mean and standard

deviation would predict. However, the distribution

has fat tails; extreme changes occur once in a while,

and much more often than would be expected from a

normal distribution. Budget changes follow a

leptokurtic distribution, and the cumulative

frequency of observations is related with a power

function to the size of the change.

This does not only apply to U.S. budget outlays

but is a very strong empirical result. A massive

amount of empirical evidence confirms that budget

Prange F. and Serritzlew S..

A Really Simple Explanation of Policy Punctuations? - Interdependence, Complexity, and Policy Punctuations.

DOI: 10.5220/0004055300970102

In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),

pages 97-102

ISBN: 978-989-8565-20-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

changes follow this distribution, in different

countries, states, municipalities. James True calls

such budget changes avalanches (True 2000).

Figure 1: Real U.S. Budget Outlays, 1800-1994. Note:

Copied from Jones, Sulkin & Larsen (2003: 164).

Sometimes the avalanches are small and affect

only limited parts of the system, sometimes the

avalanches gain momentum and cause dramatic

changes. The tricky part is that it is impossible to

predict when these avalanches occur, both in sand

piles and in budgets. Studies of actual sand piles

have revealed clear patterns of how often it happens,

and of the frequency of avalanches of certain sizes,

but it has proved extremely hard to predict exactly

where and when it occurs (Bak, 1996: 59ff.). The

same is true for public budgets. It is easy to predict

how many avalanches appear within a reasonable

period of time, but the timing usually comes as a

surprise.

This phenomenon calls for an explanation. Two

explanations are available in the literature.

According to the theory of punctuated equilibria

(Baumgartner & Jones, 1993; Jones, Baumgartner &

True, 1998), long periods of stability in political

subsystems, where most decisions are made, will,

once in a while, be broken or punctuated when a

political issue is elevated unto the macro political

level or becomes subject to intense media attention.

This may produce dramatic changes. Consistent with

this explanation, Jones, Baumgartner & True (1998)

find that dramatic changes occur, and that they

cannot be explained simply by exogenous shocks,

and Danish and UK data show that leptokurtosis is

more prevalent in some policy areas than in others.

The authors suggest that explanations for this might

be factors such as international conflict and party

preferences (John and Margetts, 2003: 427).

Explanations based on the interplay between

political subsystems and the macro political arena

and on information processing are definitely

relevant, and account for empirical variation in the

amount of leptokurtosis. But one puzzle is still left.

If the avalanches are caused by the differences in

institutions, in policy areas, in media attention or

due to friction or to over-emphasis on certain signals

from the outside world, how come that avalanches

seems to be omnipresent? The empirical studies

show that budget changes nearly always follow a

leptokurtic distribution. If these factors were the

only possible causes of this phenomenon, should we

not expect it not to occur in some instances?

In the following, we identify four simple

characteristics, which must apply to any budgeting

process. We argue that complex patterns of policy

punctuations is a result of these four characteristics

alone, and develop a simulation which show that this

is indeed true. Specifically, we hypothesize that,

even in a system with no outside intervention, with

perfectly normally distributed input signals, with no

overemphasis on certain signals, no institutions, and

with no friction, leptokurtosis will, due to interaction

among multiple agents, still prevail. This conjecture

is based on the following four simple observations,

which must be true of any budgeting process.

Without someone requesting and allocating funding,

there would be no budgeting activity at all (Schick,

1988: 63). Therefore, in any budgeting process:

(1) Several actors (beggars) request and spend

budgets

(2) Several actors (philanthropists) allocate funding

Funding is requested partly because any

organization or program needs some resources to

survive; insufficient funding will, at some point, lead

to closure or radical transformation. Programs,

institutions, agencies, or other entities which depend

on public money which do not receive sufficient

funding will eventually close down. This means that:

(3) Beggars which do not receive sufficient funding

will eventually close down

Budgeting is about allocating resources between

several different purposes. This means that any

budgeting process involves several different actors

requesting funding, and there is always a possibility

that new ideas or programs will appear. Finally,

budgeting is only relevant if funding is limited and

smaller than the sum of all requests for funding. If

this were not the case, money could just be

distributed, and budgeting would not be relevant at

all. This completes the list of the four observations:

(4) Available funding is limited and often smaller

than requested funding

Therefore, in budgeting, actors are

interdependent. This is easy to see. Since funding is

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

limited (4), some actors request funding (1) from a

closed set of funding opportunities (2), and is

required to do so in order to survive (3), the fate of

one particular actor in the budgeting process

depends on how successful others are. If there are

many competitors, and if they receive a very large

share of the available funding, it is harder to get

sufficient funding. If competitors collapse or

disappear, more resources will be available for

others. The four simple observations therefore imply

that budgeting takes place in a complex

interdependent system. Interestingly, complex

systems of interdependent parts tend to produce

leptokurtic distributions. This happens when

complex systems during prolonged periods of

relative stability self-organize into a critical state.

When in a critical state, the system is likely to

experience a major change.

This brief account of budgeting and complexity

does not, of course, substantiate the claim that the

four simple observations on budgeting imply

leptokurtosis. In order to do this, we simulate a

simple budgeting game adhering to the four

observations.

2 THE SIMULATION

In our simulation some actors, called beggars, are

capable of applying for funding from several

possible sources, which are called philanthropists.

Beggars seek to optimize their appropriations.

Beggars and philanthropists obey a set of simple and

minimalist rules which are congruent with the four

observations. All input into the simulation is drawn

randomly from a normal distribution. The question

is then whether the output is also normally

distributed or leptokurtic.

In this section the simulation is described. We begin

with a verbal explanation of the basic logic in the

simulation, and how it can be interpreted. We then

schematically present it in more detail.

Beggars and philanthropists interact as shown in

Figure 2. First, beggars request funding (point 1 of

the observations). They spend money and generate

(or use) savings. Second, philanthropists allocate

funding among applicants and send appropriations

(point 2). If appropriations continue to fall short of

spending, savings of the beggar will eventually be

exhausted. The beggar then closes down and

disappears (point 3). Philanthropists have limited

possibilities to provide funding, and there is always

a demand from beggars of funding (point 4).

Budget requirement

Spending

Savings

Available funding

Budget request

Appropriation

Beggar

Philanthropist

Figure 2: The relation between a beggar and a

philanthropist.

The chances of getting funding depends the

familiarity of a beggar to a philanthropist. This is

modeled spatially. The beggars and philanthropists

are located in a grid of, say, the size 10 x 10. This

gives 100 possible locations. The various locations

of the philanthropists in space can be interpreted as

their association with a certain sector, with certain

types of projects, or a certain policy area. If a beggar

is close to a philanthropist, it means that the

proposal of the beggar seems relevant and familiar

from the perspective of the philanthropist. The

distance from a beggar to a philanthropist represents

familiarity. For instance, an interpretation of a

beggar being located next to a philanthropist would

be that the beggar provides a service, which is well

known to and highly prioritized by the

philanthropist. Conversely, a beggar located far

away from any philanthropist is trying to get funding

for a really arcane project or purpose, which no

philanthropist is likely to prefer to support.

A beggar can only apply for funding from one

philanthropist. Beggars move in order to be close to

an attractive philanthropist, but movement is

penalized. Moving is tantamount to redefining or

reformulating the funding proposal in order to

accommodate a new philanthropist. The distance

moved to be located next to a philanthropist

therefore affects the opportunity to get funding. If a

beggar does not have to move, it is well known by

the philanthropist and is therefore likely to get

funding. If a beggar must move a long distance, it is

less likely to get funding. If a beggar has moved a

long distance, the philanthropist will be more likely

to consider cutting the budget request. This happens

when the beggar is selected for review. If the beggar

has moved the maximum possible distance, the

beggar will always be selected. If the beggar has not

moved since the last iteration, the risk of review is

equal to the base risk at 50%. As we return to below,

this, and other central values can be varied. We

systematically vary these parameters in our analysis

to check the robustness of the results.

If a beggar received all requested funding in last

iteration, the beggar stays with the philanthropist. If

not, the beggar seeks for a more attractive

philanthropist. The beggars find the most attractive

A Really Simple Explanation of Policy Punctuations? - Interdependence, Complexity, and Policy Punctuations

philanthropist, move if necessary, and receive

funding. If funding is insufficient, savings are

reduced, and if saving fall below zero, the beggar

disappears. If funding is sufficient, the beggar starts

over in the next iteration. The philanthropists receive

applications, and allocate appropriations.

In the first three stages, the simulation is

initialized. The action takes place in the remaining

six stages, which are repeated in a large number of

iterations. In the first stage of the simulation the n ×

n grid is created. The size of the grid is determined

by a parameter called [Size]. In the second and third

stage, several beggars and philanthropists are

created. For each beggar, a budget to be requested is

determined; for each philanthropist, funding to

allocate is determined, both random numbers drawn

from a normal distribution with a specific mean and

standard deviation (both are parameters). The exact

number of beggars and philanthropists are set as

parameters. Their location in the grid is determined

randomly. This completes the initialization in the

first three stages.

The action takes place in the remaining six

stages. These stages are iterated a large number of

times. In stage four, budget needs are determined for

each beggar. This is the amount the beggar will

spend. Budget needs is a fraction of the budget

requirements, calculated as a random number from a

normal distribution with mean 0.98 times the budget

requirement. Beggars then select a philanthropist. If

a beggar in the previous iteration got full finding, it

will stick to the same philanthropist as in last

iteration. If not, it will locate visible philanthropists,

and choose the most attractive one, based on a

calculation of the expected payoff for each visible

philanthropist.

In stage five, funding is allocated. The

philanthropists collect the budget requests, and

determine whether the available funding is

sufficient. If it is, the beggars get what they request.

If the sum of requests for funding exceeds the

amount available, the philanthropist will select

beggars for review. The likelihood of being selected

is base risk (a parameter) at 50% + a movement

penalty. If no beggars were selected, the procedure

is repeated. In stage six, the beggars spend money

according to the budget needs. The surplus (or

deficit) of a beggar is added to its savings. In stage

seven, the state of the world is printed to a file.

Beggars with negative savings are eliminated. In

stage eight, new beggars are generated if the sum of

available resources exceeds the sum of requested

funding. In stage nine, the positions of the beggars

are updated, and the budget requests of each beggar

changes by a random number drawn from a normal

distribution. The beggars and philanthropists then

start over at stage four in the next iteration.

3 THE DISTRIBUTION OF

BUDGET CHANGES

We now analyze the distribution of changes in

appropriations in subsets of different sizes. The

smallest subset consists of 9% of the grid. On

average, such an area encompasses 4-5

philanthropists and 18-20 beggars. The beggars, of

course, may have options outside of the area, and are

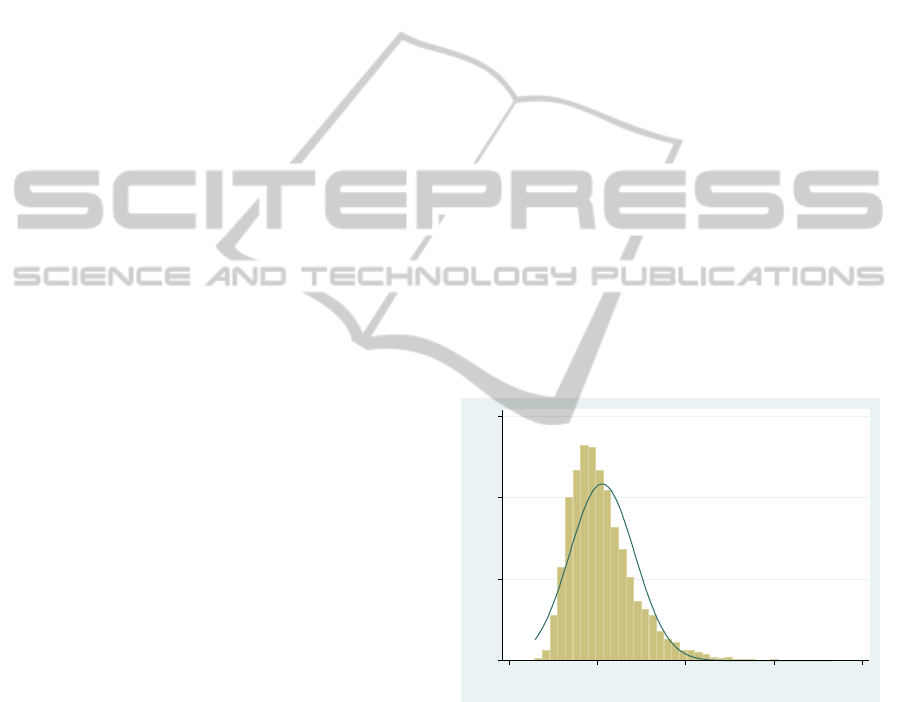
able to move in and out. For the 9%-subset, Figure 3

shows a histogram for changes in appropriations for

the default parameters in a simulation with 10,000

iterations with a superimposed normal distribution

with same mean and standard deviation as the

distribution of changes in appropriations. A visual

inspection reveals that the distribution is non-

normal. Changes in appropriations tend to have a

higher peak, and more dramatic changes occur than

would be expected from a normal distribution.

Similar simulations have been carried out for 959

other configurations of parameters.

1.5

Density

-1 0 1 2 3

Percent change in appropriations

Figure 3: Histogram for changes in appropriation for 9%-

subset. Standard parameters.

On average, the l-kurtosis value for these 960

distributions is 0.203. This is clearly higher than the

l-kurtosis score for the normal distribution. Hence,

in the smallest subset, the typical distribution is

leptokurtic. However, it is not always the case. Of

the 960 simulations, 1% has distributions below

0.112, and 5% below 0.124. Although it is quite

rare, and although l-kurtosis values are typically

above 0.1226 (the value for a normal distribution),

some of the simulations end up with normal or even

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

100

almost uniform distributions.

Figure 4 shows average l-kurtosis scores for

different subsets. It is clear the l-kurtosis score is

negatively related to the size of the subset. The

figure shows the average l-kurtosis scores (0.203 for

the 9% subset) along with the scores for the 25th and

75th percentiles. The horizontal line shows the l-

kurtosis scores for a normal distribution. As the

subset becomes larger, the l-kurtosis scores drop.

They are always, also at the system level where

100% of the grid is analyzed) on average above the

score of a normal distribution, but when the subset is

larger than 50%, only slightly so. The percentile

spikes indicate that it becomes increasingly common

that some of the simulations, even though the

average is above 0.1226, fall below the score of the

normal distribution.

Hence, the simulations show that leptokurtosis is

quite common in analyses of subsets of the system,

and that the l-kurtosis scores are quite low compared

to empirical distributions of budget changes.

Furthermore, the tendency to leptokurtosis becomes

smaller when for larger subsets, and almost

disappears at the system level. We infer from this

that leptokurtosis at the subsystem level is almost

always a consequence of the four simple

observations that we argue must be true of any

budgeting process. We also infer that the four

observations cannot account for the much larger l-

kurtosis scores typically observed in empirical

distributions. Hence, the four simple observations

can account for why leptokurtosis is omnipresent,

but they cannot account for the magnitude of

leptokurtosis.

.12 .14 .16 .18

.22

0 .2 .4 .6 .8 1

Size

Percentile75/Percentile25 lkurtosis

NormalDist

Figure 4: L-kurtosis scores for different subsets. 960

simulations with varying parameters.

This is consistent with the empirical findings that

leptokurtosis is an fact systematically related to

factors such as different features of policy areas,

characteristics of information processing, differences

in decision costs, and variations in the institutional

setting (Jones & Baumgartner, 2005a; 2005b;

Breunig, 2007; Jones, Sulkin and Larsen, 2003;

Breunig and Koski, 2006). All of these factors are

held constant in this simulation. What are not held

constant are the parameters. The analyses are based

on 960 simulations with different configuration of

parameters.

4 CONCLUSIONS

We know quite a lot on how public budgets change.

They tend, most of the time, to be remarkably stable.

This is the classical instrumentalist insight.

However, an equally important part of budgeting is

that, once in a while, very large changes occur.

Changes in budgets follow a leptokurtic distribution.

This seems to be an omnipresent phenomenon. In

this paper we conjecture that leptokurtosis is a very

fundamental feature of public budgeting. We argue

that four simple observations, that should be true of

any budgeting process, are enough to account for

leptokurtosis. We investigate the implications of the

four observations by designing a simple simulation

of a budgeting game between beggars and

philanthropists adhering to the observations. It turns

out that the four observations do in fact imply

leptokurtosis at the subsystem level. However, the

observations and the simulation do not predict as

large l-kurtosis scores as is typically found in

empirical distributions of changes in budgets.

Ockham’s razor seems, in this case, to be too blunt

an instrument. This leads us to conclude that

leptokurtosis is in fact a very fundamental feature of

public budgeting, and that this is likely to be part of

the explanation of why leptokurtosis is omnipresent.

However, it is only part of the explanation. To

understand differences in leptokurtosis and the

magnitude of leptokurtosis, other explanations are

necessary. Fortunately, these explanations are

available in the empirically based literature on

policy punctuations and budgeting.

REFERENCES

Bak P. (1996). How Nature Works. New York: Copernicus

Baumgartner, Frank R. & Bryan D. Jones (1993). Agendas

and Instability in American Politics, Chicago:

University of Chicago Press.

Baumgartner, Frank R., Martial Foucault & Abel François

(2006): “Punctuated equilibrium in French budgeting

A Really Simple Explanation of Policy Punctuations? - Interdependence, Complexity, and Policy Punctuations

101

processes”, Journal of European Public Policy, vol.

13 (7), pp. 1086-1103.

Breunig, C. and C. Koski (2006): “Punctuated Equilibria

and Budgets in the American States”, Policy Studies

Journal, 34 (3), 2006.

Breunig, Christian (2007). Institutions, Attention Shifts,

and changes within National Budgets, Ph.D.-

dissertation, University of Washington.

Davis, Otto A., M. A. H. Dempster and Aaron Wildavsky

(1966): “A Theory of the Budgetary Process”,

American Political Science Review 60 (3), 1966

John, P. and H. Margetts (2003): “Policy Punctuations in

the UK: Fluctuations and Equilibria in Central

Government Expenditure since 1951”, Public

Administration, 81 (3), 2003.

Jones, B. D., F. R. Baumgartner and J. L. True (1998):

“Policy Punctuations: US Budget Authority, 1947–

95”, Journal of Politics, 60, 1998.

Jones, B. D., T. Sulkin & H. A. Larsen (2003): “Policy

Punctuations in American Political Institutions”;

American Political Science Review 97 (1), 2003

Jones, Bryan D. & Frank Baumgartner (2005a): ”A Model

of Choice for Public Policy”, Journal of Public

Administration Research and Theory, vol 15, pp. 325-

351.

Jones, Bryan D. & Frank Baumgartner (2005b): The

Politics of Attention, Chicago: Chicago University

Press.

Padgett, J. F. (1980): “Bounded Rationality in Budgetary

Research”, American Political Science Review, 74,

1980.

Schick, Allen (1988). “En Enquiry into the Possibility of a

Budgetary Theory”, in Rubin, Irene S. (ed.), New

Directions in Budgetary Theory, New York: State

University of New York Press.

True, J. L. (2000): “Avalanches and Incrementalism:

Making Policy and Budgets in the United States”,

American Review of Public Administration, 30 (1),

2000.

Wildavsky, A. (1984): The Politics of the Budgetary

Process. Little, Brown and Company, Boston.

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

102