Finding a Tradeoff between Compression and Loss in Motion

Compensated Video Coding

Thomas Guthier

1,2

, Adrian Sosic

, Volker Willert

and Julian Eggert

Control Theory and Robotics, TU Darmstadt, Landgraf-Georg Strasse, Darmstadt, Germany

Honda Research Institute Europe, Offenbach, Germany

Keywords:

Video Coding, Polynomial Motion Model, Quadtree Segmentation, Model Selection.

Abstract:

In video coding, afﬁne motion models combined with a quadtree decomposition have often been suggested

as an extension to the mostly used translational models combined with a blockwise decomposition. What is

missing so far is a thorough analysis to judge the tradeoff between using more complex motion models or more

elaborate decomposition methods in terms of data compression and information loss. In this paper, we compare

different polynomial motion models with a quadtree decomposition concerning motion model complexity

and granularity of decomposition. We provide a statistical evaluation based on optical ﬂow databases to

quantitatively ﬁnd a tradeoff between bitrate and reconstruction error.

1 INTRODUCTION

One of the most important aspects in modern video

coding are motion compensation algorithms. Those

algorithms segment each image of the sequence and

describe the local motion of each segment. This mo-

tion information is then used to predict the recent im-

age given the image of the previous timestep. The

use of the temporal correlation in image sequences

can drastically reduce the bitrate. In lossy video cod-

ing, the quality of the compressed video will decrease

because of prediction errors of the motion compen-

sation. Therefore the quality requirements must be

balanced with bitrate requirements. While video cod-

ing standards like MPEG-4 or H.264 (Wiegand et al.,

2003) use only block-wise segmentation and purely

translational models to describe the local motion, a

lot of research focuses on more sophisticated motion

models and segmentation methods. An overview on

the recent development in video coding can be found

in (Sikora, 2005). For example (Zhang et al., 1997)

use a hierarchical segmentation including a quadtree

decomposition and afﬁne models for motion com-

pensation. Their algorithm shows good results con-

cerning reconstruction quality and bitrate reduction

in highly structured scenes, but the bitrate exceeds

the coding standards in scences with little motion

due to the extra parameters needed for their com-

plex segmentation. (Karczewicz et al., 1997) use a

quadtree based segmentation along with polynomial

(a) (b)

Figure 1: On the left is an example image and on the right

the corresponding color coded ﬂow ﬁeld. The color value

codes the moving direction and the intensity the amplitude

of the motion. The lines show the quadtree segmentation.

motion models. The quadtree segmentation is easy

to implement and needs only one extra bit per seg-

ment compared to a regular block-wise segmentation

when using an efﬁcient coding as described in (Sulli-

van and Baker, 1994). Their video coding algorithm

showed good results concerning both reconstruction

quality and compression, but is not realtime capa-

ble due to a complex coefﬁcient selection algorithm

which is needed to reduce the number of bits en-

coding the polynomial motion models. (Lakshman

et al., 2010) focus on adaptivemotion model selection

to overcome the problem of the multiple parameters

needed to encode higher order polynomial models.

Although research is focusing on extensions of the

simple translational model and the block-wise decom-

position, little has been done to study the complex

interdependencies between the reconstruction quality,

Guthier T., Sosic A., Willert V. and Eggert J..

Finding a Tradeoff between Compression and Loss in Motion Compensated Video Coding.

DOI: 10.5220/0004057000810084

In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems

(SIGMAP-2012), pages 81-84

ISBN: 978-989-8565-25-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

the required number of bits, the segmentation algo-

rithm and the different model orders. The reconstruc-

tion quality depends on two elements: The model or-

der and the segmentation. A higher model order and

a ﬁner segmentation both increase the reconstruction

quality, but then again increase the number of bits.

An open question is, whether an increased model or-

der can increase the reconstruction quality and addi-

tionally lead to a coarser segmentation and therefore

lower the overall required bitrate at the same time. Or

if on the other hand, a ﬁner segmentation with simpler

motion models yields better results.

The topic of this paper is twofold. The ﬁrst

achievement is a statistical analysis of the gain in re-

construction quality for increasing the order of poly-

nomial motion models. The second achievement is

the analysis whether it is a better strategy to spend

more bits on the segmentation and less on the model

complexity or vice versa. For the purpose of com-

parison two segmentation algorithms are used. One

simple block-wise segmentation familiar to the one

used in the MPEG4 standard and a quadtree de-

composition. Because this research focuses on mo-

tion compensation and not on an entire video cod-

ing algorithm, all experiments are directly done on

ground truth optical ﬂow datasets and not on image

sequences.

2 ALGORITHM

In the following pixel positions in the images are de-

scribed by ~x = (x, y)

⊤

and ﬂow ﬁelds are given by

the correspondingﬂow vectors~v(~x) = (v

(~x), v

(~x))

⊤

As a measurement of the reconstruction quality we

deﬁne the reconstruction error E

∑

k~v(~x

) −

~v(~p

,~x

. k · k

is the Euclidean norm,

~v(~x

) =

( ¯v

(~x

), ¯v

(~x

))

⊤

is the model of the optical ﬂow and

= number of pixels per segment.

With s = num-

ber of segments, we get the normalized reconstruction

error E =

∑

2.1 Linear Parametric Models

The model order is N, the coefﬁcients for v

(~x) are

~a = (a

,...)

⊤

and for v

(~x) are

b = (b

,...)

⊤

Polynomial models can be described by

We choose the reconstruction error instead of the more

popular PSNR to distinguish that we compare the ﬂow

model to the ideal ﬂow ﬁeld and not the gray value pixel

values with the ones warped by the ﬂow model.

¯v

(~x) =

∑

n=0

∑

i=0

n−i,i

n−i

¯v

(~x) =

∑

n=0

∑

i=0

n−i,i

n−i

Each segment has its own parameter vector ~p

(~a,

b). The number of parameters per model is

= 2

∑

n=0

∑

i=0

1 = (N + 1)(N + 2). (1)

The model of order N = 0 is the translational model

and has 2 parameters. The ﬁrst order model is the

afﬁne model with 6 parameters. The model param-

eters are estimated by minimizing the reconstruction

error.

2.2 Segmentation

There are two parameters controlling the segmenta-

tion process. The quality parameter ε and the max-

imum segmentation level l

max

. l is the segmentation

level. The algorithm for each segment is:

1. Calculate the model parameters p

2. Calculate the normalized reconstruction error E

3. If E

< ε ∨ l = l

max

⇒ stop. Else, continue

with step 4.

4. Divide the segment into four rectangluar seg-

ments. Increase the segmentation level counter

and continue for each new segment at step 1.

One result of this quadtree segmentation can be seen

in Fig. 1. For ε = 0 the algorithm has zero tolerance to

model errors and is likely to segment the entire ﬂow

ﬁeld into equally sized rectangluar blocks until l

max

is reached. This is comparable to the block-wise de-

composition proposed in the MPEG4 standard.

2.3 Dependency of Segmentation Level

and Model Order

Some dependencies have a theoretic nature and can be

directly derived from the formulars. In the following,

we show under which conditions a quadtree decom-

position leads to less parameters than a block-wise

decomposition and how increasing the model order

and the maximum segmentation level increases the bi-

trate. Let q be the number of parameters needed to

encode one timestep of a motion compensation algo-

rithm. When using block-wise decomposition (index

), no parameter is needed to encode the segmenta-

tion. For the quadtree decomposition (index

) one

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications

0 1 2 3 4 5 6

−3

−2

−1

Segmentation Level

Reconstruction Error (log)

0. Order

1. Order

2. Order

3. Order

4. Order

Figure 2: Mean value of the reconstruction error depend-

ing on the segmentation level for two optical ﬂow datasets.

Each curve shows a different motion model.

extra parameter per segment is needed for the encod-

ing. We now compare the number of parameters q

versus q

with q

= s

·q

and q

= s

·(q

+ 1). The

inequality q

≤ q

leads to

≤

. For low model

orders the number of quadtree segments s

has to be

smaller than the number of block segments s

to make

the quadtree decomposition more effective than the

block-wise segmentation. For higher model orders

the fraction

converges towards one. Therefore

the inﬂuence of the extra bit for the quadtree decom-

position is decreasing. Next we analyze the increase

of q

due to an increase of N and l for a block-wise de-

composition. The number of segments s

(l) = 4

ex-

ponentially depends on the segmentation level l. With

eq. (1) we get q

(l, N) = (N + 1)(N + 2)4

and the

gain in q

∆q

b,l

= q

(l + 1,N) − q

(l, N) = 3(N + 1)(N + 2)4

∆q

b,N

= q

(l, N + 1) − q

(l, N) = 2(N + 2)4

∆q

b,l

∆q

b,N

(N + 1). (2)

Incrementing the segmentation level leads to extra

bits compared to incrementing the model order, de-

pending linearly on the model order.

3 SIMULATION RESULTS

3.1 Error Depending on Model Order

Segmentation is done with the block-wise decompo-

sition even though the quadtree decomposition shows

comparable results. The analysis is done on the en-

tire sequences of the CSAIL (Liu et al., 2008) and

Middelbury (Baker et al., 2007) database, which pro-

vide ground truth optical ﬂow. The databases contain

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08

Reconstruction Error

Number of Parameters (log)

Level 2

Level 3

Level 4

Level 5

Level 6

block−wise

Figure 3: Number of parameters depending on the recon-

struction error for different segmentation levels. The algo-

rithm using the afﬁne motion model was applied to the car

sequence.

complex sequences with moving objects as well as

homogeneous regions and sequences with little mo-

tion. The curves in Fig. 2 show the mean values of all

sequences.

The curves are almost parallel throughout the dif-

ferent segmentation levels. Therefore the results are

independent of the segmentation quality. Increasing

the model order from translational to afﬁne causes

the most segniﬁcant increase in reconstruction qual-

ity. From eq. (2) we conclude that incrementing the

model order increases the bitrate less than increment-

ing the segmentation level. We now give an example

how this information can be applied to Fig. 2. We

start with the translational model (+) at the segmen-

tation level 3. The logarithmic reconstruction error is

≈ 1 and if we want to achieve ≈ 0 we can either in-

crease the segmentation level or the model order by

two. Because of eq. (2) latter is preferable.

3.2 Error and Bitrate Depending on the

Segmentation Level

In the following we use the afﬁne model. Fig. 3

shows the results for different parameters l

max

and ε.

The algorithm was applied to the highly structured

car sequence of the CSAIL database that is shown in

Fig. 1. The simulations were performed for the other

sequences as well with comparable results. The seg-

mentation algorithm as described in Sec. 2 depends

on two parameters, the maximum segmentation level

max

and the quality parameter ε. If ε is set a low value

little errors are tolerated leading to a stronger segmen-

tation. Larger ε lead to higher reconstruction errors,

but less parameters. Each curve represents one l

max

and different ε, starting with ε = 0. The pareto front is

marked. For each bitrate and reconstruction error, the

FindingaTradeoffbetweenCompressionandLossinMotionCompensatedVideoCoding

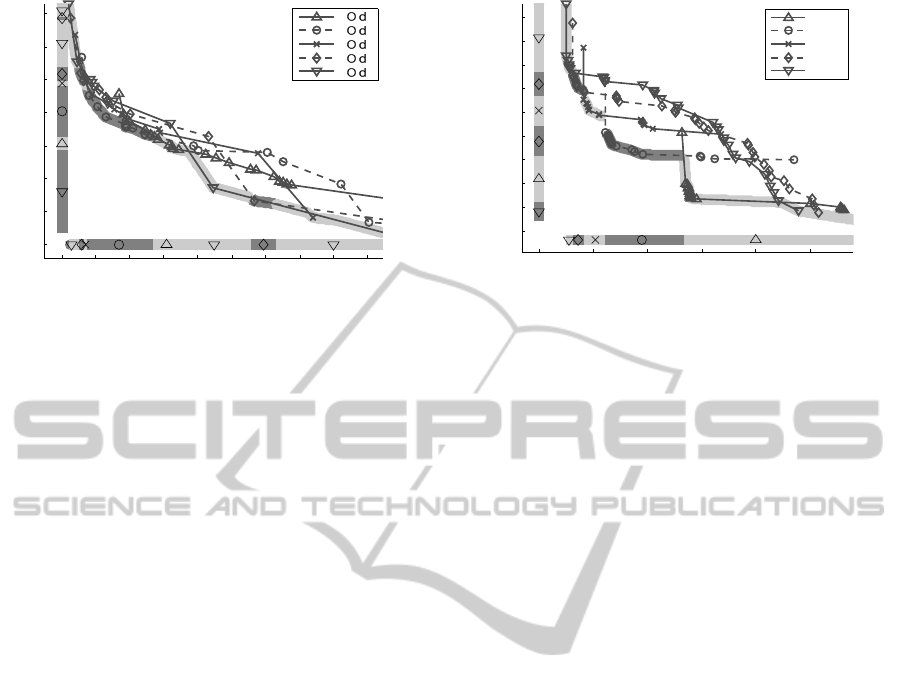
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09

Reconstruction Error

Number of Parameters (log)

0. r er

1. r er

2. r er

3. r er

4. r er

Figure 4: Number of parameters depending on the recon-

struction error for different motion models. The algorithm

segmented to the ﬁfth level was applied to the car sequence.

ideal segmentation level is marked on the pareto front

that is additionally plotted next to the axis. The points

corresponding to a block-wise segmentation for each

max

are additionally marked in Fig. 3.

As discussed in Sec. 2 the block-wise segmenta-

tion yields the same reconstruction error as the corre-

sponding graph with ε = 0, but needs less parameters

to encode. From the points on the pareto front we

can conclude that the desired reconstruction quality

or bitrate can be achieved by adapting the segmenta-

tion level. There is no overall best segmentation level,

rather an ideal level for the different requirements.

3.3 Error and Bitrate Depending on the

Model Order

Next we ﬁx the segmentation level l

max

= 5 and com-

pare the differentmodel orders and variousquality pa-

rameters ε. The results on the car sequence are plot-

ted in Fig. 4. Fig. 5 shows the same algorithm on

the hand sequence of the CSAIL database which has

on the one hand a lot of motion discontinuities and

on the other hand large homogeneous regions. Each

curve represents one polynomial motion model and

different ε, starting with ε = 0. Like in Fig. 3 the

pareto front is marked and additionally plotted with

the corresponding model next to the axis. For both

sequences there are regions on the pareto front where

one model gives the best tradeoff between bitrate and

reconstruction quality. Small reconstruction errors re-

fer to larger models.

4 CONCLUSIONS

We provide a qualitative and quantitative analysis for

motion compensation in video coding to ﬁnd the best

0 0.5 1 1.5 2 2.5

7.5

8.5

9.5

10.5

11.5

Reconstruction Error

Number of Parameters (log)

0.Order

1.Order

2.Order

3.Order

4.Order

Figure 5: Number of parameters depending on the recon-

struction error for different models. The algorithm seg-

mented to the ﬁfth level was applied to the hand sequence.

tradeoff given compression and loss constraints. It is

possible to judge which segmentation granularity and

motion model complexity best fulﬁlls the coding re-

quirements. The results stress the need for coding al-

gorithms that are adaptive in both the segmentation

level and motion model order.

REFERENCES

Baker, S., Scharstein, D., Lewis, J. P., Roth, S., Black, M. J.,

and Szeliski, R. (2007). A database and evaluation

methodology for optical ﬂow. In Proc. IEEE Conf.

ICCV.

Karczewicz, M., Nieweglowski, J., and Haavisto, P. (1997).

Video coding using motion compensation with poly-

nomial motion vector ﬁelds. Signal Processing: Im-

age Communication, 10(1-3):63 – 91.

Lakshman, H., Schwarz, H., and Wiegand, T. (2010). Video

coding with cubic spline interpolation and adaptive

motion model selection. In SPCOM, Conf.

Liu, C., Freeman, W. T., Adelson, E. H., and Weiss, Y.

(2008). Human-assisted motion annotation. In Proc.

IEEE Conf. CVPR, pages 1–8.

Sikora, T. (2005). Trends and perspectives in image and

video coding. IEEE J.PROC., 93(1):6–17.

Sullivan, G. J. and Baker, R. L. (1994). Efﬁcient quadtree

coding of images and video. IEEE J.PROC., 3.

Wiegand, T., Sullivan, G., Bjontegaard, G., and Luthra, A.

(2003). Overview of the h.264/avc video coding stan-

dard. IEEE Transactions on CSVT, 13(7):560 –576.

Zhang, K., Bober, M., and Kittler, J. (1997). Image se-

quence coding using multiple-level segmentation and

afﬁne motion estimation. Selected Areas in Commu-

nications, IEEE Journal on, 15(9):1704 –1713.

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications