On the Development of Totally Self-checking Hardware Design for

the SHA-1 Hash Function

Harris E. Michail

, George S. Athanasiou

, Andreas Gregoriades

, George Theodoridis

and Costas E. Goutis

Electrical Eng. and Information Technology Dept., Cyprus University of Technology, Kyprianos Str., Lemesos, Cyprus

Electrical and Computer Engineering Dept., University of Patras, Rio Campus, 26500, Patras, Greece

Computer Science and Engineering Dept., European University of Cyprus, Nicosia, Cyprus

Keywords: Cryptography, Hash Functions, SHA-1, Totally Self-checking, Concurrent Error Detection.

Abstract: Hash functions are among the major blocks of modern security schemes, used in many applications to

provide authentication services. To meet the applications’ real-time constraints, they are implemented in

hardware offering high-performance and increased security solutions. However, faults occurred during their

operation result in the collapse of the authentication procedure, especially when they are used in security-

critical applications such as military or space ones. In this paper, a Totally Self-Checking (TSC) design is

introduced for the currently most-used hash function, namely the SHA-1. A detailed description concerning

the TSC development of the data- and control-path is provided. To the best of authors’ knowledge, it is the

first time that a TSC hashing core is presented. The proposed design has been implemented in 0.18μm

CMOS technology and experiments on fault caverage, performance, and area have been performed. It

achieves 100% coverage in the case of odd erroneous bits. The same coverage is also achieved for even

erroneous bits, if they are appropriately spread. Compared to the corresponding Duplicated-with-Checking

(DWC) design, the proposed one is more area-efficient by almost 15% keeping the same frequency.

1 INTRODUCTION

Cryptographic hash functions are properly-

developed algorithms that are used by security

systems to provide authentication services. An

application domain of hash functions is the

verification of the integrity of the exchanged

messages. For this reason, hash function are

employed in digital signature algorithms like DSA

(NIST, 2002a) and other applications, such as the

Secure Electronic Transaction (Loeb, 1998) and

Public Key Infrastructure (NIST, 2001).

Additionally, hash function is the major building

block of the Hashed Message Authentication Code

(HMAC) (NIST, 2002b), of the Internet Security

protocol (IPSec) (NIST, 2005) of the forthcoming

Internet Protocol (IPv6) (Loshin, 2004).

As hash functions are used in real-time

applications, they must be properly implemented to

offer high throughput, secure, and reliable solutions.

The hardware implementation of the hash functions

offers high-speed proccesing and secure

encapsulation, however, a crucial issue arises when

these systems are used in high-noisy enviroments

(e.g. space or military applications). In that cases,

potential errors during their normal oparation have

to be timelly detected. In the last years, the

development ofsecurity algorithms (hash functions

and block ciphers) with Concurrent Error Detection

(CED) capabilities is a very active research (Juliato,

2008), (Juliato, 2010). CED is the common method

to develop self-checking designs, where the Circuit

under Test (CuT) is partitioned to its major units and

each of them is, then, redesigned applying CED

techniques. A more robust subset of the self-

checking circuits is the Totally Self-Checking

(TSCs) circuits (Lala, 2001).

In this paper, a TSC, 4-staged, pipelined design

for the SHA-1 hash function is introduced. For each

component of the architecture a detailed desrciption

concerning its development as a TSC is given. The

proposed TSC design achieves 100% fault covarage

for the odd faulty bits, while, in some caes, even

faulty bits are detected as well. The introduced

design is implmented in TSMC 0.18μm technology

and experimental results regarding the frequency,

270

E. Michail H., S. Athanasiou G., Gregoriades A., Theodoridis G. and E. Goutis C..

On the Development of Totally Self-checking Hardware Design for the SHA-1 Hash Function.

DOI: 10.5220/0004059302700275

In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 270-275

ISBN: 978-989-8565-24-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

throughput and area were gathered. An additional

design using only the Duplication-with-Checking

(DWC) method has been also developed in the

above technology for comparison reasons. Based on

the experimental results, the proposed TSC desing

achieves the same throughput as the DWC one but it

is almost 15% more area-efficient.

The rest of the paper is organized as follows. In

Section 2 the majority of the related published

works, regarding error detection and/or correction is

security IPs, is reported. Section 3 describes briefly

the background for SHA-1 hash function and CED

principles. In Section 4 the introduced TSC hashing

core is analytically presented. The experimental

results, for error detection capability and

performance, of the introduced TSC core are shown

in Section 5, while Section 6 concludes the paper.

2 RELATED WORK

In the literature, there are several published works

concerning the application of error detection and/or

correction in cryptographic IPs. However, such

designs have mainly been proposed for block ciphers

(Karri, 2002); (Bertoni, 2003); (Karri, 2002).

Considering the application of error

detection/correction principle on hash functions, few

published works exist in the literature. In (Ahmad,

2007), error detection with parity coding was

applied in SHA-512 hash function transformation

round and implemented in FPGA technology. In

(Juliato, 2010), a fault tolerant hardware design of

the HMAC on top of SHA-256 and SHA-512 hashes

is presented. Similar work is also presented in

(Juliato, 2008), dealing only with the SHA-256 hash

function core. In both of the above works, the fault

tolerance principle was applied only in the registers

of the utilized designs. To the best of authors

knowledge, it is the first time that a TSC design is

developed including the message schedule and

control units. Furthemore, the adopted design

procedure is generic and can be also applied (with

slight modifications) to other existing hash functions

(e.g. SHA-256, RIPEMD) due to the similarities of

their components.

3 BASIC BACKGROUND

3.1 SHA-1 Hash Function and Design

SHA-1 hash function is an iterative algorithm that

operates on 512-bit message blocks and returns a

160-bit output, h, that is called message digest. A

message schedule procedure is applied on the

message blocks to produce the W

values, which are

fed to the corresponding t-th iteration of the

transformation round. The transformation round

takes as input the W

value, a constant value, K

defined by the standard, and the initial values, H

(0)

(in the first iteration) or the values produced in the

previous iteration, performs the transformation

processing, and generates through 80 iterations a

series of hash values. The last generated hash value

is considered as the message digest, h.

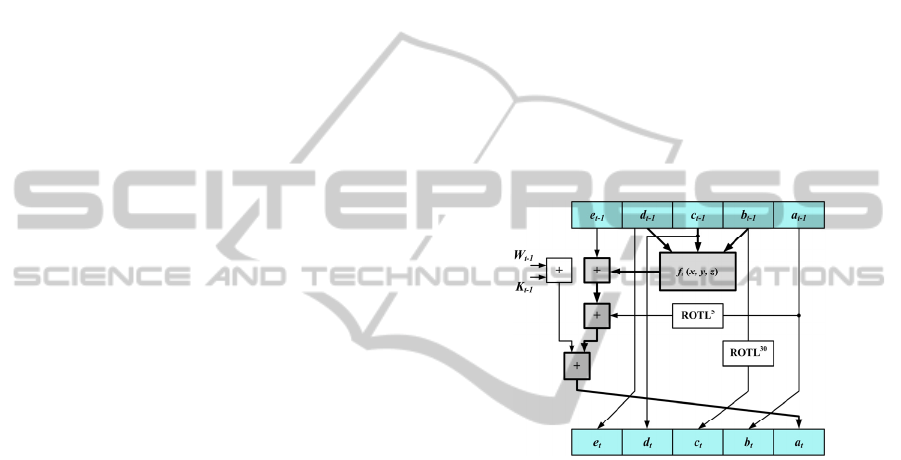
The SHA-1 transformation round (Figure 1)

includes simple additions, rotations, and four Non-

Linear Functions (NLFs). These NLFs functions

consist of simple XOR, AND, and NOT logical

operations. More information about SHA-1

algorithm can be found in (NIST, 2008).

Figure 1: SHA-1 transformation round.

At the t-th iteration (t = 1, 2,…,80), it receives

five 32-bit words, namely the (a

t-1

– e

t-1

) ones,

performs the computations shown in Figure 1, and

produces the output values (a

– e

). Concerning the

production of the W

values, the first 16 of them are

produced by a simple splitting of the 512-input

block into 16 32-bit words. The remaining 64 are

produced through Eq. (1),

(

)

381416

, 16 t 79

ttttt

WROTLWWW W

−−− −

⊕⊕ ⊕ ≤≤

(1)

where ROTL

stands for x times left bit rotation and

⊕

for XOR.

As mentioned in the introduction, the target

architecture is a 4-stage pipeline one because it

offers a balanced compromise in terms the achieved

throughput and area. The target architecture includes

four pipeline stages with each one includes a Round

unit i (i = 1, 2, 3, and 4), which corresponds to the

hash transformation round (see Figure 1), a W unit

for producing the W

values, and a memory, K, for

storing the constant values. Also, pipeline registers

OntheDevelopmentofTotallySelf-checkingHardwareDesignfortheSHA-1HashFunction

271

exist at the output of each Round unit. The W unit

blocks comprise XOR trees, as described before (see

Eq. 2). The control logic includes four counters and

each pipeline stage executes 20 iterations of the

transformation round.

3.2 CED Techniques

The use of CED introduces redundancy in the

produced design, which may be hardware, time, or

information redundancy. Hardware redundancy

refers the duplication of the CuT and checking the

outputs (Duplication-with-Checking or DWC). On

the other hand, time redundancy techniques re-

compute the output of the CuT at different time

instances with the same circuit. Finally, information

redundancy concerns the appending of data with

extra bits produced by a coding scheme (e.g. parity

coding) in order to detect potential errors (Lala,

2001).

A more robust subset of self-checking circuits is

the Totally Self-Checking circuits (TSCs). In order a

circuit to be TSC, it has to satisfy the self-testing and

fault secure properties. Self-testing means that for

every fault of an assumed fault set the circuit

produces a non-codeword at the output for at least

one input codeword. On the other hand, the fault-

secure property ensures that for any fault in the

assumed fault set, the circuit’s output is either a

correct codeword or a non-codeword (Lala, 2001).

Compared to a system developed using the

genral CED principle, a TSC one offers important

benefits. Specifically, in a TSC design except the

data errors, errors ocured at the included checking

circuitry are also detected. Also, a TSC system is

more efficient in terms of area and throughput than a

DWC one. Finally, contrary to DWC system, the

corrsponding TSC one allows laocating the faulty

component. Thus, it can be re-designed in case of

continuous failing, without much effort.

4 TSC SHA-1 CORE

In this section the proposed TSC SHA-1 core is

described. We start presenting the general topology

of the TSC components that are developed.

Afterwards, the TSC design of the data path and

control units components are described. In the end,

the finalization of the TSC core is developed.

4.1 Topology of the TSC Components

To produce the TSC SHA-1 core, both information

redundancy (parity coding) and hardware

redundancy (DWC) are utilized. The choice between

them is made taking into account the introduced area

penalty and the incapability of applying information

redundancy in some circuit blocks.

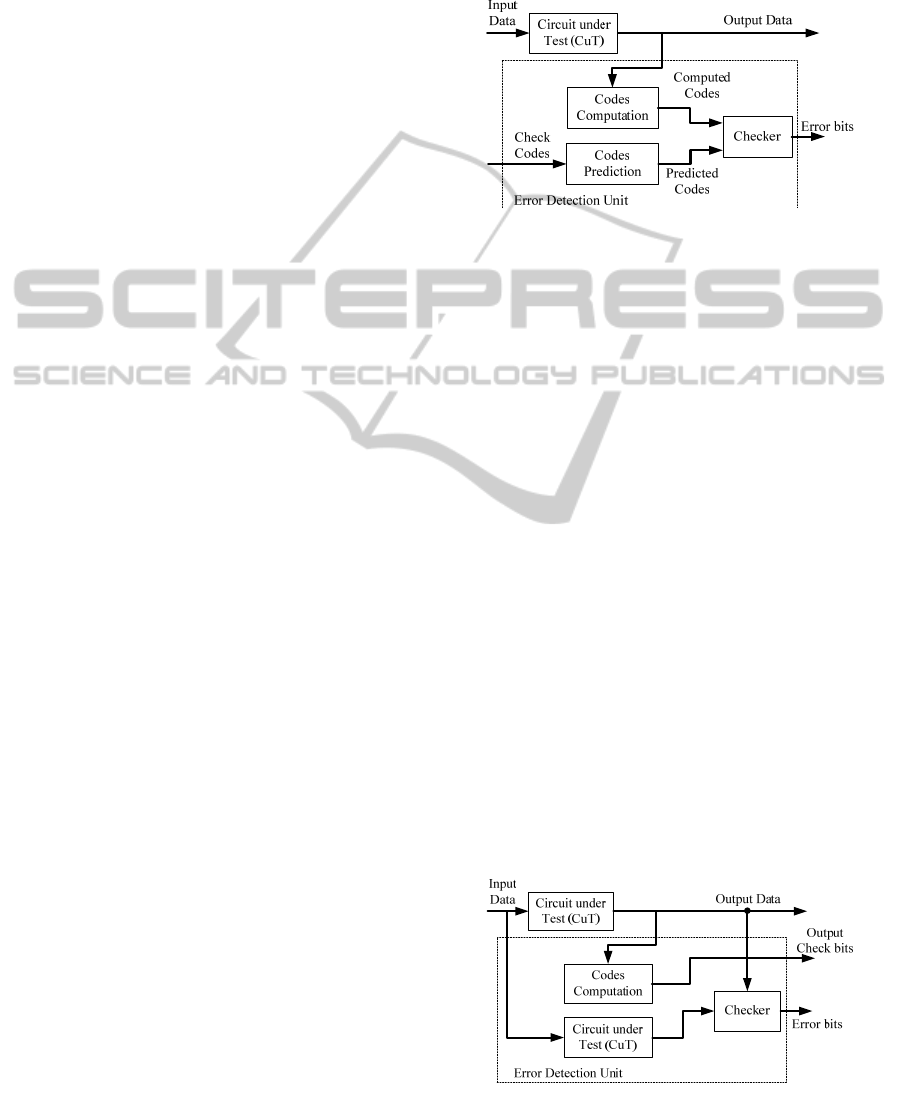
Figure 2: Block diagram of a TSC component based on

information redundancy.

According to Figure 2, a TSC module consists of

the Circuit under Test (CuT) and the Error

Detection unit. Furthermore, the Error Detection unit

includes three components which are the Codes

Prediction, the Codes Computation, and the Checker

units. As the CuT and the Code Prediction unit are

separate circuits without common parts, the TSC

principle is validated.

The role of the Codes Prediction unit is to predict

the codes (check bits) of the CuT output. In our case,

this unit is a parity prediction unit that predicts the

parities of the output data using the parity bits of the

incoming data. The Codes Computation unit is used

for computing the codes of the output (i.e. the

complement check bits) using the produced output

data of the CuT. Finally, the Checker performs the

comparison between the predicted and computed

codes and produces the error signal.

When DWC is applied, the block diagram of the

TSC module is shown in Figure 3. This diagram is

similar to that of Figure 3 with the exception that the

CuT is duplicated, while the Codes Prediction unit is

omitted. However, there is still a Codes

Computation unit for producing the output’s code

that is going to be fed in the next TSC circuit.

Figure 3: Block diagram of a TSC based on DWC.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

272

The Checker unit used in this work is an r-bit

Two Rail Checker (TRC) circuit. It receives two

inputs say X = (X

, X

) and its complement X’ = (X’

X’

), compares them and produces two outputs Z and

Z’ which are complementary if there are not faulty

input bits. Moreover, the TRC fulfils the TSC

principles ass stated previously and can detect faults

potentially occurred during its own operation.

Hence, it does not affect the TSC nature of the

whole design. This type of TRCs has a special

property (Anderson, 1971): There is a great

similarity between a part of the TRC and a parity

generator. Hence, exploiting the incorporated TRC

we can produce parity bits from a TSC sub-circuit

implemented with hardware redundancy. This way,

the produced TSC designs are more area-efficient,

because: a) TSC blocks using hardware redundancy

and TSC blocks using information redundancy are

easily connectable and b) in cases where hardware

and information redundancy techniques are used at

the same time in a TSC module, the data parities are

produced by the incorporated TRC.

4.2 TSC Modules of the SHA-1 Design

A) TSC adders. The addition components contain

two computational paths, which are the sum and

carry computation ones. The above computation

paths are described by Equation 2, letting S

and C

be the sum and carry outputs of the i-th stage, where

0 ≤ i ≤ n-1:

()()

iii ii

XYX XY

−

=⊕⊕

⎡⎤

⎡

⎤

=⊕ +⊕

⎣

⎦

⎢⎥

⎣⎦



(2)

In order to develop a TSC adder unit, the sum and

carry computation paths have to be checked without

sharing common logic for checking. Regarding the

sum path, the parity bit, P

, for each byte of the sum

output is calculated as follows:

()

() ()

()

111

000

Sii

nnn

iii

XYC

PXY

PPP

−−

−

−−−

−

===

== ⊕⊕

=⊕⊕

∑∑

∑∑∑

(3)

where P

and P

are the parities of the X, Y inputs.

The P

is the parity of the (i-1)-bit carry array. The

sum parity prediction can be performed through

adding resources for the above mentioned 3-input

XOR operation. The parities of the X and Y data are

already known and fed as input in the parity

prediction unit. Regarding the parities of the carries,

they have to be computed. However, the carry

computation path has to be checked independently

from the sums one. Thence, the direct computation

of P

from the carries and its usage in Eq. 3 would

violate the TSC principle.

Exploiting the special property of the TRC

circuits that was mentioned in Sub-section 3.2, the

production of the P

bits can be done using a DWC

scheme for the carry bits along with a TRC. The

block diagram of a TSC adder is shown in Figure 4.

Figure 4: TSC 32-bit modulo adder.

B) TSC NLFs and Sole Rotators. Concerning these

components, the effectiveness of applying the parity

scheme and constructing a Parity Prediction Unit has

to be investigated. For a significant amount of these

components, the application of the parity coding

scheme leads to a TSC design that is more complex

and therefore more area consuming than the

corresponding DWC one. Hence, for those

components the DWC scheme is followed. If the

parity prediction unit is able to be formed, it is

implemented with the minimum possible area

penalty.

Regarding the NLFs, the only one that is more

efficient to be implemented using the parity coding

scheme is the Par function, while all the others are

implemented using the DWC scheme. The TSC Par

block is similar with the one depicted in Figure 3.

The topology of the other two TSC NLFs (Ch, Maj)

is shown in Figure 3. Regarding the sole rotators that

exist in the transformation round of SHA-1 hash

function, they realize bit-level rotations. The

exploited parity bit scheme in this paper operates on

bytes. Thus, the complexity of parity prediction is

highly increased, tending to be infeasible. Therefore,

the TSC rotators are implemented using the DWC

scheme, similarly to Figure 4.

C) TSC Registers and Multiplexers. In registers and

multiplexers the input is transferred to output

OntheDevelopmentofTotallySelf-checkingHardwareDesignfortheSHA-1HashFunction

273

unchanged without performing any processing.

Hence, the parity coding can be applied easily. The

corresponding block diagram of these TSC

components is similar with the one shown in Figure

D) Message Scheduling Units. As described in Sub-

section 3.1, the message scheduling for each round

is performed by a shift-register, a W unit block and a

2to1 32-bit MUX. The MUX is transformed to TSC

as described in 4.2.1B and shown in Figure 3. The

16x32-bit shift register consists of 16 32-bit registers

consecutively connected to perform the 32-bit data

shifting. Hence, the corresponding TSC shift register

consists of 16 TSC cells (registers), which are

implemented as described in (C). The incorporated

XOR tree is developed to TSC using information

redundancy and its topology is similar to the one of

Figure 2.

E) Control Units. The development of the control

unit components (counters) to TSC ones begins with

an appropriate modification of them, namely the

production of complementary pairs of the control

signals. This is required because the control signals

have to be checked without violating the TSC

principle. This action introduces minor delay in the

control unit’s process, because its components are

simple counter blocks. The application of parity

coding in the counter blocks leads to TSC ones that

consume more area than the DWC ones. Therefore,

the TSC transformation is accomplished by applying

the DWC scheme along with a TRC for the output’s

checking, similarly to Figure 3.

4.3 Finalization of the TSC SHA-1

Core

At this point, all the components of the SHA-1

function, together with the majority of their

interconnections have been developed fulfilling the

TSC principle. However, there is a possibility of

either concurrent utilization of information and

hardware redundancy for data buses, or existence of

control signals that are checked neither during their

production, nor before their consumption. Thus,

some interconnections may allow some errors to

pass undetectable.

Regarding the first type of the above issues,

typical examples are the bus branches just before the

DWC nodes. The data from the same bus are

transferred to both the main and the duplicated

module. Hence, there is a possibility that a fault

occurs just before the branch and the error will be

transferred to both the above modules and not be

detected. In order to deal with such cases, a

complement parity generation and checking is

performed just before the main and the duplicated

module. The problems of the unchecked control

signals are addressed via some additional resources

(TRCs) for checking the complementary pairs of

control lines that serve as inputs in a component.

The same also holds for the Control Unit’s

components themselves. The complementary pairs

are produced either by the current Control Unit

itself, or by other similar Unit of the current core.

5 EXPERIMENTAL RESULTS

The TSC SHA-1 core that was developed was

captured in VHDL, validated for its functionality by

using a large set of input test vectors, and

implemented in TCMC 0.18μm CMOS technology.

Each individual TSC component of the TSC

SHA-1 design was tested for a large number of test

cases targeting different types of potential errors, in

order to validate its error detecting ability. To model

multiple odd faulty bits, a single fault was injected,

while the multiple even faulty bits were modelled by

two appropriately injected erroneous bits.

Concerning the first case, a single fault was injected

consecutively in every bit of a selected input of each

TSC component. The achieved detection was 100%.

Regarding double fault injection, two error bits are

considered: the first one for all the bits of the first

two bytes and the second one for all the bits of the

remaining two bytes of the input quantity. This way,

an even number of errors in the input quantity will

be set for detection. The achieved error detection

was again 100%.

Regarding the performance evaluation, three

metrics were exploited, namely the frequency (F),

the Area (A) and the Throughput (T). The frequency

and the area were obtained by the employed tool,

while the throughput was computed by Eq. (4):

bits F

Throughput

cycles

⋅

(4)

where #bits refer to the number of the processed

bits, #cycles corresponds to the required clock

cycles between successive messages to generate

each hash value, and F is the frequency.

To the best of authors’ knowledge, there is no

previously published work in the literature

presenting complete TSC hashing cores. Therefore,

the comparisons were made among: a) The hashing

core without error detection, b) The TSC hashing

core and c) The DWC hashing core. It has to be

mentioned that, all the CED techniques introduce

SECRYPT2012-InternationalConferenceonSecurityandCryptography

274

some kind of delay in the critical path. In order to

fairly evaluate the proposed TSC core, the frequency

among the three core versions under comparison was

kept the same.

In Table 1, the performance metrics for the SHA-

1 hash function’s architectures, implemented in

0.18μm CMOS technology, are presented. As it can

be seen, the TSC SHA-1 core introduce an area

overhead of 69%, compared to the SHA-1 core

without any form of CED in the same operating

frequency. However, it is more efficient compared to

DWC SHA-1 core, by almost 15%.

Table 1: Performance evaluation results for SHA-1 hash

function’s designs.

Design F(MHz)

Area

(kgates)

Throughput

(Gbps)

SHA-1 without CED

350

45.1

8.96

SHA-1 DWC

350

89.7

8.96

Proposed TSC SHA-1

350

77.6

8.96

6 CONCLUSIONS

This paper proposed a TSC design of the SHA-1

hash function. The resulted fault detection for odd

faulty bits is 100%, while, in some cases, even faulty

bits are detected as well. The TSMC 0.18μm CMOS

implementation of the resulted TSC core, proved

that the introduced TSC core is more area-efficient,

than the corresponding DWC one. Future work will

be mainly focused on developing TSC designs of the

other functions of the SHS family and other hashes.

REFERENCES

Ahmad, D., I., Das, A., S., 2007. Analysis and detection of

errors in implementation of SHA-512 algorithms on

FPGAs. In Int. Journal of computer Oxford University

Publishing,, vol.50, no.6, pp.728-738.

Anderson, D., A., 1971. Design of Self-Checking Digital

Networks Using Coding Techniques. Doctoral

Dissertation. CSL/Univ. Illinois, Urbana, rep. n.527.

Bertoni, G., Breveglieri, L., Koren, I., Piuri, V., 2003.

Error analysis and Detection Procedures for Hardware

Implementation of the Advance Encryption Standard.

In Computers, IEEE Transactions on , vol.52, no.4,

pp. 492- 505.

Juliato, T., M., Gebotys, C., 2008. SEU-resistant SHA-256

designs for Security Satellites. In 10

Workshop on

Signal Processing for Space Communications (SPSC)

Conference, pp.1-17. Greece, EU.

Juliato, T., M., Gebotys, C., 2010. An efficient fault-

tolerance technique for the Keyed-Hash Message

Authentication Code. In International Conference on

Aerospace, IEEE, pp.1-17. Big Sky, MT.

Karri, R., Wu, K., Mishra, P., Kim, Yongkook, 2001.

Fault-Based Side-Channel Cryptanalysis Tolerant

Rijndael Symmetric Block Cipher Architecture. In

International Symposium on Defect and Fault

Tolerance in VLSI Systems. pp.427-435. San

Francisco, CA, USA.

Karri, R., Wu, K., Mishra, P., Kim, Y., 2002. , Concurrent

Error Detection Schemes for Fault Based Side-

Channel Cryptanalysis of Symmetric Block Ciphers.

In Computer-Aided Design of Integrated Circuits and

Systems (CAD), IEEE Transactions on, vol.21, no.12,

pp. 1509- 1517.

Lala, P., K., 2001. Self-Checking and Fault Tolerant

Digital Design. Morgan Kaufman Publishers. San

Francisco, USA.

Loeb, L., 1998. Secure Electronic Transactions:

Introduction and Technical Reference. Artech House

Publishers. Norwood, USA.

Loshin, P., 2004. IPv6: Theory, Protocol and Practice,

Elsevier Publications. USA.

NIST, 2001. Introduction to Public Key Technology and

the Federal PKI Infrastructure. SP 800-32., NIST, US

Department of Commerce Publications, USA.

NIST, 2002a. Digital Signature Standard Federal

Information Processing Standard. FIPS

186-1 NIST,

Department of Commerce Publications, USA.

NIST, 2002b. The Keyed-Hash message authentication

code (HMAC). NIST-FIPS 198, NIST, US

Department of Commerce Publications, USA.

NIST, 2005. Guide to IPSec VPN’s. NIST-SP800-77,

NIST, Department of Commerce Publications, USA.

NIST), 2008. Secure Hash Standard (SHS). NIST-FIPS

180-3, Department of Commerce Publications, USA.

OntheDevelopmentofTotallySelf-checkingHardwareDesignfortheSHA-1HashFunction

275