
The Application of Evolutionary Algorithm for the Linear Dynamic
System Modelling
Ivan Ryzhikov and Eugene Semenkin
Institute of Computer Sciences and Telecommunication, Siberian State Aerospace University,
Krasnoyarskiy Rabochiy ave., 31, Krasnoyarsk, 660014, Russia
Keywords: Linear Dynamic System, Linear Differential Equation, Evolutionary Strategies, Parameters Identification
Problem, Structure Identification.
Abstract: The approach to dynamic system modelling in the linear differential equations form is presented. The given
approach fits the identification problems with the system output observations sample and the input sample
even if the output data is distorted by a noise. The structure and parameters identification problem is
reduced to a global optimization problem, so that every solution consists of the model structure and its
parameters. This allows searching the analytical model in the ordinary differential equation form with any
limited order. The analytical model delivers a special benefit in its further use in the control and behaviour
estimation problem.
1 INTRODUCTION
There are many different approaches to make a
model of the dynamic system. The identification
task itself depends on the given structure and the
parameters estimation special technique. Also, the
practice need tends one to make the model in an
analytical form so it would be easier to find out a
control function or predict the system behaviour
with different input functions or initial points. We
can approximate the system output and use the
special technique to define its unit step function
reaction or we can make the model in a dynamic
form. The model that was built as an approximation
with a function base is not as useful and flexible as a
dynamic model. Moreover, the task would be
reduced to the enumerative technique for the
different combination of functions, while we do not
know, for example, the order of equation or
multiplicity of characteristic equation roots. In the
article (Janiczek, Janiczek, 2010) we can see an
identification method in terms of fractional
derivatives and the frequency domain. The
information about the plant is taken from the given
frequency domain and not from the output
observations that could be distorted. Also, special
control and regulation methods are required to the
model in fractional derivatives. We can use
stochastic difference equations (Zoteev, 2008), and
build a model using the output observations,
observations of the reaction on the step excitation.
This approach is partially parameterized, i.e., the
order and functional relation between the system
state and previous states are unknown. In (Parmar,
Prasad, Mukherjee, 2007), the dynamic system
approximation with the second order linear
differential equations is examined. The coefficients
are determined with the genetic algorithm. In this
paper, there is the description of the structure and
parameters identification task solving by means of
the reduction of the identification task to a real value
optimization problem with the modified
evolutionary strategies method. The algorithm
workability and usefulness are demonstrated on the
real identification problem.
The rest of the paper is organised in the
following way. In Section 2 we describe the problem
statement of the system structure and parameters
estimation, in Section 3 the modified hybrid
evolutionary strategies algorithm for the ordinary
differential equation identification is described, in
Section 4 we fulfill modelling the chemical reaction
with described approach, and in Conclusion we
summarise our results.
234
Ryzhikov I. and Semenkin E..
The Application of Evolutionary Algorithm for the Linear Dynamic System Modelling.
DOI: 10.5220/0004060402340237
In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),
pages 234-237
ISBN: 978-989-8565-20-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 STRUCTURE AND
PARAMETERS ESTIMATION
PROBLEMS
Let us have a sample
, , , 1,
i i i
y u t i s
, where s is its
size,
i
yR
are dynamic system output
measurements at
i
t
, and
()
ii
u u t
are control
measurements. It is also known, that the system is
linear and dynamic, so it can be described with the
ordinary differential equation (ODE):
( ) ( 1)
10
()
kk
kk
a x a x a x b u t
,
0
(0)xx
.
(1)
Here
0
x
is supposed to be known. In the case of
the transition observation, we can put forward a
hypothesis about initial point: the system output is
known at initial time and the derivative values can
be set to zero, because usually the system
observation starts in its steady state. In general, the
initial point can be approximated. Using the sample
data we need to identify parameters and the system
order
m
, which is assumed to be limited, so
,m M M N
.
M
is a parameter that is set by the
researcher. This value limits the structure of the
differential equation, i.e., it limits the ODE order. It
is also assumed that there is an additive noise
: ( ) 0, ( )ED
, that affects the output
measurements:
()
i i i
y x t
.
(2)
Without information on the system order, we
would not be able to solve the identification task, but
because of the maximum order limitation, the task
can be partially parameterized. The maximum order
is supposed to be chosen a priori. It would specify
the optimization problem space dimension.
Without loss of the generality, let the leading
coefficient of ODE be the constant equal to 1, so that
( ) ( 1)
10
()
kk
k
k k k
aa
b
x x x u t
a a a
(3)
or
( ) ( 1)
1
()
kk
k
x a x a x b u t
.
(4)
Then we can seek the solution of the identification
task as a linear differential equation with the
order
m
,
( ) ( 1)
10
ˆ ˆ ˆ ˆ ˆ ˆ
()
mm
m
x a x a x a u t
,
0
ˆ
(0)xx
,
(5)
where the vector of equation parameters
10
ˆ ˆ ˆ ˆ
0, , 0, , , ,
T
n
m
a a a a R
,
1nM
,
delivers an extremum to the functional
1
ˆ
ˆ
( ) ( ) min
n
N
ii
aR
i
aa
I a y x t
.
(6)
In general case, the solution
ˆ
()xt
is evaluated with a
numerical integration method, because the control
function has no analytical from, rather is given
algorithmically. We prefer the criterion (6) instead
of quadratic criteria because of its robustness. For
the correct numerical scheme realization, let us have
a coefficient restriction for equation (3),
0.05
k
a
.
Otherwise, this parameter is going to be equal to
zero, so
0, 1
k
a m m
. That condition prevents
extra computational efforts of the numerical
evaluation scheme and is necessary for the local
optimization algorithm effecting on the system
structure.
Now let us consider the specific modelling
issue. The identification of linear differential
equations system is connected with the optimization
problem for the system of equations:
()
00
1
()
o
i
n
i k i i i
k i i j j i
j
ji
a x a x b x b u t
,
(7)
where
____
, 1,
i
x i n
, is an observed system output;
o
n
is
the number of outputs.
Equation (7) shows that the system is
considered not in general way and every system
output depends on other outputs but not on their
derivatives. Also, there is only one control input for
every equation. This can be easily extended to the
case with many control inputs.
The identification problem for the system with
equation (7) is important and an ability to solve it
could be useful. And it is clear, that the functional
(6) can be transformed into the functional
11
ˆ
ˆ
( ) ( ) min
o
n
N
j
i j i
a
ji
aa
I a y x t
(8)
for the given systems by means of the same
transformation that was made for a single output
system.
The Application of Evolutionary Algorithm for the Linear Dynamic System Modelling
235

3 MODIFIED HYBRID
EVOLUTIONARY STRATEGIES
ALGORITHM FOR ORDINARY
DIFFERENTIAL EQUATION
IDENTIFICATION
The reason why the modification of an evolutionary
strategies algorithm was used is that the
identification problem leads to solving the
multimodal optimization task. The goal of the given
approach is the identification of the parameters and
the structure simultaneously. The system structure
and its parameters can be represented by one vector.
The criterion (8) for this vector is complex and
sensitive to the vector components changed by
stochastic search operators. This is why we have to
develop the specific modification for the global
optimization technique.
As a method to seek the task (8) solution, the
hybrid modified evolutionary strategies (Schwefel,
1995) method was chosen. Let every individual be
represented with tuple
______
, , ( ) , 1,
i i i
iI
H op sp fitness op i N
,
where
____
, 1,
i
j
op R j k
, is the set of objective
parameters of the differential equation;
____
, 1,
i
j
sp R j k
, is the set of strategic
parameters;
I
N
is the population size;
1
( ): (0,1], ( )
1 ( )
k
fitness x R fitness x
Ix
is the
fitness function.
As the selection types, proportional, rank-based
and tournament-based selections were chosen. The
algorithm produces one offspring from two parents
and every next population have the same size as
previous. Recombination types are intermediate and
discrete. The mutation of every offspring’s gene
happens with the chosen probability
m
p
. If we have
the random value
{0,1}, ( 1)
m
z P z p
, which is
generated for every current objective gene and its
strategic parameter then
(0, )
offspring offspring offspring
i i i
op op z N sp
;
(0,1)
offspring offspring
ii
sp sp z N
,
where
2
( , )Nm
is the normally distributed random
value with the mean
m
and the variance
2
.
We suggest a new operation that could increase
the efficiency of the given algorithm. For every
individual, the real value is rounded down to the
nearest integer. This provides searching for solutions
with near the same structure.
Also for
1
N
randomly chosen individuals and
for
2
N
randomly chosen objective chromosomes we
make
3
N
iterations of local search with the step
l
h
to determine the better solution. This is the random
coordinate-wise optimization.
4 MODELLING OF THE
CHEMICAL REACTION
We need to develop a model in the form of
differential equations for the chemical reaction. The
process of the hexadecane disintegration is
considered, the concentration of the output products
are measured. Using the sample of measurements we
can build up a model with the modified evolutionary
strategies algorithm.
The settings of the algorithm were chosen
according to the previously conducted numerical
experiments with some randomly generated systems
where their use has given the best performance.
The disintegration of the hexadecane gives the
following products: the spirits and carbonyl
compounds. The initial point is known. There is no
control input in this identification problem. We set
the maximum order for the first equation to 10. The
50 runs of the algorithm gave us some different
solutions that are shown in Table 1.
As we can see, the found parameters and system
structure forms the first order differential equation,
and that fact does not contradict the hypothesis
(Romanovskii, 2006), which states that
disintegration chemical reactions can be presented as
first order linear differential equation.
Knowing the structure of the equations we can
identify the system itself. The given optimization
procedure is a stochastic algorithm, that is why the
best solution from the 20 runs was taken.
Table 1: The hexadecane disintegration model.
Models and the error (I)
4.05 0.9 1, 0.3022x x I
1.05 0.4 1, 0.2834x x I
2.1 0.55 1, 0.1822x x I
1.05 0.15 6.85 0.9 1, 0.227x x x x I
3.4 0.45 0, 0.202x x I
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
236
The solution can be represented in the matrix form
0.1671 0.7630 0.3625
0.0413 0.3428 0.115
0.0026 0.405 0.327
A
,
0.3477
0
0
B
.
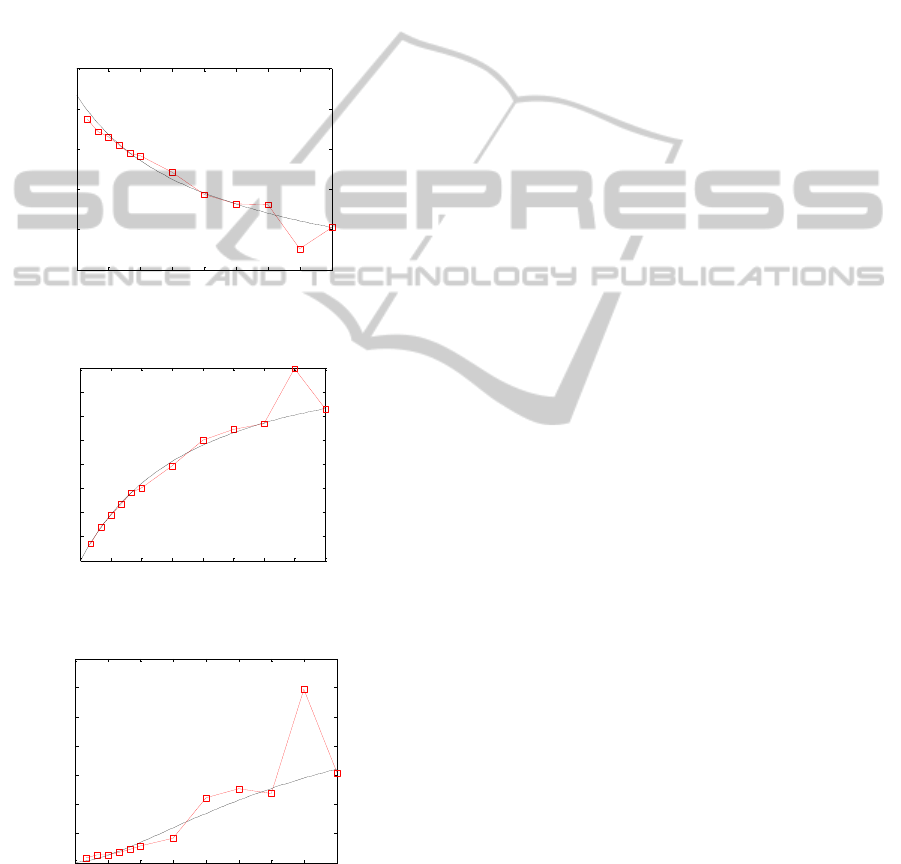
The system outputs and the sample are shown on
figures 1, 2 and 3 for hexadecane, spirits and
carbonyl compounds respectively.
0 1 2 3 4 5 6 7 8
3.5
4
4.5
5
5.5
6
Figure 1: Hexadecane concentration measurements and the
model output.
0 1 2 3 4 5 6 7 8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Figure 2: Spirits concentration measurements and the
model output.
0 1 2 3 4 5 6 7 8
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Figure 3: Carbonyl compounds concentration
measurements and the model output.
As we can see on figures, the measurement at the
point
7t
is an abnormal measurement, but it did
not effect on the model.
5 CONCLUSIONS
In this paper, the method of the ordinary differential
equation structure and parameters identification was
described. Within the proposed approach the system
structure and its parameters are automatically
determined. The suggested modifications of the
evolutionary strategies algorithm increase the
accuracy of model and allow solving two tasks at the
same time. The identification problem for
hexadecane disintegration reaction was considered.
Numerical experiments have demonstrated the
proposed approach usefulness.
The further investigation should be concentrated
on the estimation of the performance of algorithm
with the different local optimization and mutation
parameters.
REFERENCES
Janiczek T., Janiczek J., 2010. Linear dynamic system
identification in the frequency domain using fractional
derivatives. Metrol. Meas. Syst., Vol. XVII, No 2, pp.
279-288.
Parmar G., Prasad R., Mukherjee S., 2007. Order
reduction of linear dynamic systems using stability
equation method and GA. International Journal of
computer and Infornation Engeneering 1:1.
Romanovskii B. V., 2006. The foundations of the chemical
kinetics. Moscow: Ekzamen
Schwefel Hans-Paul, 1995. Evolution and Optimum
Seeking. New York: Wiley & Sons.
Zoteev V., 2008. Parametrical identification of linear
dynamical system on the basis of stochastic difference
equations. Matem. Mod., Vol. 20, No 9, pp 120-128.
The Application of Evolutionary Algorithm for the Linear Dynamic System Modelling
237
