Modeling Cell Populations in Development using Individual Stochastic

Regulatory Networks

Paweł Bednarz and Bartek Wilczy

nski

Institute of Informatics, University of Warsaw, Banacha 2, Warsaw, Poland

Keywords:

Stochastic Simulation, Cellular Population, Regulatory Network, GPU Computing.

Abstract:

We present a new approach to high level stochastic simulations of cell populations. The proposed method

employs the Stochastic Logical Network (SLN) method for simulating independent regulatory processes oc-

curring in individual cells allowing for efﬁcient simulations of systems consisting of thousands of cells. The

stochastic logical network model is extended to account for not only regulatory control of gene expression

but other related processes such as: inter-cellular signaling, cell division and programmed cell death. In the

paper, we present the method and several case studies, where the proposed approach is used to provide models

of biological phenomena. These examples include community effect in gene expression, the role of negative

feedback in growing epithelial cell lineage and the role of asymmetric cell division in cell fate choices. We

present also an efﬁcient implementation of the method using GPU computing and show that its performance

is signiﬁcantly better than that using CPU.

1 INTRODUCTION

Modeling biological processes linked to gene regula-

tion is a very broad and diverse ﬁeld. The problem is

fundamental and many different approaches with dif-

ferent advantages and disadvantages have been pro-

posed to address its various aspects (see (De Jong,

2002) for a review). In particular, development of

multi-cellular organisms presents many challenges as

it requires consistent models taking into account large

populations of cells able to perform their regulatory

programs independently but at the same time able to

communicate with each other via chemical signaling.

In addition, the developmental systems need to be ro-

bust to external conditions and at the same time, they

rarely operate under equilibrium conditions, requir-

ing models capable of capturing temporal behavior

as well as analysis of possible attractors and steady

states of the system. In addition, frequently possible

states of the system differ only by a small number of

molecules leading to stochastic behavior on a single-

cell level.

Boolean networks have been particularly useful

in modeling developmental systems (Thomas and

D’Ari, 1990), as they do not require exact rate con-

stants and they provide the modelers with models

which are relatively easy to study. However, most of

the systems are focusing on cell autonomous be-

havior, with notable exceptions of several exam-

ples of networks related to Drosophila segmentation

anchez et al., 2008) or wing disc (Gonzalez et al.,

2008), however even those pioneering works have

only considered at most a handful of cells at once.

2 PROPOSED MODEL

We propose a new approach to modeling large cell

populations with explicitly simulating regulatory net-

works of each of the cells. The method is based on

stochastic logical networks (SLN), a generalization

of the Boolean network model which builds up upon

the non-deterministic state transitions in Boolean net-

works and deﬁnes a probabilistic model of state tran-

sitions. In the following sections we will brieﬂy de-

scribe the SLN framework and how we use it for the

purpose of simulating cell populations.

2.1 From Boolean Networks to

Stochastic Logical Networks

Boolean networks have a long history of applications

to gene regulatory systems. Early work by Kauffman

(Kauffman, 1977) and Thomas (Thomas, 1978) led to

the representation of the regulatory network as a sys-

334

Bednarz P. and Wilczy

nski B..

Modeling Cell Populations in Development using Individual Stochastic Regulatory Networks.

DOI: 10.5220/0004060703340340

In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),

pages 334-340

ISBN: 978-989-8565-20-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tem of Boolean equations. For example a simple neg-

ative feedback loop can be represented by two equa-

tions:

X ← Y

Y ← −X

In those ﬁrst simple models of regulatory net-

works the dynamics was usually considered to be syn-

chronous, i.e. all genes changed their value to their

respective regulatory function (right-hand side of the

regulatory equation). While the simplicity of such an

approach might be appealing, it is now well known

that due to very different transcription and decay rate

for different genes, it is quite far from realistic.

Later, Thomas extended this formalism and pro-

posed generalized logical networks (Thomas and

D’Ari, 1990), which not-only introduced asyn-

chronous state change for different genes, but also

extended the state space to include more than two

expression levels for some of the genes. The asyn-

chronous state change had a major impact on the anal-

ysis of the system dynamics, as now instead of a sin-

gle successor state for any state of the network we had

to consider a set of possible successor states. While

it is clear that the asynchronous state transitions are

more realistic than synchronous, they also create chal-

lenges for the formal analysis of such systems as the

size of the state space visited from any initial state can

be much larger than in the synchronous case.

More recently, we proposed another extension

of the Generalized logic formalism, by introducing

stochastic models that could be built on top of the

generalized logical networks. Stochastic logical net-

works (SLN) (Wilczynski and Tiuryn, 2006) were

originally deﬁned as continuous dynamical systems

with a canonical discretized form aimed at network

reconstruction from quantitative data (Wilczynski and

Tiuryn, 2007), however for the purposes of this arti-

cle, we will consider them to be discrete objects. Sim-

ilarly to the Boolean models, any SLN with N genes

consists of N variables g

, ..., g

each of which takes

values from a ﬁnite discrete set. For the purposes of

this article, we will consider only variables with bi-

nary value sets, but all the reasoning can be extended

to use variables with integer values and the proposed

implementation is ready to use such extended vari-

ables. The regulatory function of each gene g

is de-

scribed by an equation of the following form:

, ..., g

) =

∑

j=1

, (1)

where w

is the regulatory inﬂuence of the gene g

on g

. For any state of the network, we can cal-

culate the regulatory function for each of the genes

= {F

, ..., F

}. Given the matrix W = {w

i j

}, SLN

model deﬁnes a probability distribution

(σ) =

∑

describing the probability of changing ﬁrst the value

of gene i, given that we start from the state σ. Given

this probability distribution, we can employ an algo-

rithm, conceptually similar to the Gillespie’s stochas-

tic simulation method (Gillespie, 1977) to simulate a

cell behavior over time: in each step we select a gene

to change based on its total inﬂuence F

in comparison

to the total inﬂuence in the system.

2.2 Modeling Populations of Cells with

Stochastic Logical Networks

Starting with this slightly simpliﬁed deﬁnition of the

SLN model, we can extend it to systems consisting of

multiple cells with identical underlying genetic net-

work. To achieve this, instead of a single state σ, we

need to consider a population matrix P

i j

, where the i-

th row P[i] corresponds to a state of a single i-th cell.

With this representation, we can calculate the to-

tal inﬂuence of all genes by simply performing matrix

multiplication of P by the regulatory matrix W . Once

we have the inﬂuence, we just need to perform a sin-

gle step of the simulation for each of the cells in the

population to obtain the state of the population for the

next step.

To account for typical processes involved in gene

regulation in development, we have included addi-

tional actions performed at each step of population

simulation:

• There are special variables, regulated in the same

way as the gene variables, corresponding to the

cell division, and death. After calculating the state

of each cell, the algorithm checks whether the di-

vision or death variables are “active” and if it is

the case, it either removes the cell from popula-

tion or duplicates its row in case of symmetric di-

vision.

• For modeling signaling, a special vector is de-

ﬁned for mapping each of the genes to secreted

molecules. Each secreted molecule is described

by a positive integer. If such value is placed on

the i-th position of the secretion vector and the i-th

gene is active, a predeﬁned number of molecules

of the speciﬁed type is secreted to the environ-

ment. In case of non-secreted genes, the secretion

vector is set to 0.

• After the secretion is performed, another vector

mapping the signaling molecules back to genes is

ModelingCellPopulationsinDevelopmentusingIndividualStochasticRegulatoryNetworks

335

used. If the number of molecules of a given sig-

nal is non-zero, for each cell capable of receiving

such signal an integration event occurs randomly,

with the probability proportional to the number of

molecules divided by the number of cells in pop-

ulation.

This leads to the following algorithm:

Algorithm 1: Algorithm for a single step of STOPS simula-

tion.

Require: W : regulatory matrix

Require: P : population matrix

F ← P × W

for i=1 to N do

choose a random j according to distribution F

update P[i,j]

end for

for i=1 to N do

update Environment based on secretion from P[i]

end for

for i=1 to N do

update P[i] based on absorption from Environ-

ment

end for

for i=1 to N do

multiply or delete row P[i] based on special vari-

ables

end for

Using this algorithm, we can simulate any SLN

system provided that the matrix W , and the initial

population are speciﬁed. We have written a proto-

type implementation of this method called STOPS

(Stochastic Population Simulation) which is publicly

available on-line and was used to obtain the results

presented in the following section.

3 CASE STUDIES

In this section we describe three simple models of

small biological systems representative to questions

posed recently in the ﬁeld of modeling regulatory

networks in development. Each of those examples

illustrates different capabilities of the STOPS mod-

eling framework. All presented examples were im-

plemented in STOPS and are publicly available for

download (see Sec. 6).

3.1 Community Effect in Gene

Expression

Recent study by Saka et al. (Saka et al., 2011) pro-

posed a simple model for the community effect in

gene expression occurring during embryonic develop-

ment of Xenopus frogs. During development, when it

is necessary to create continuous tissues in the em-

bryo it is usually achieved by formation of local ag-

gregates of cells with correlated expression of a cer-

tain gene by means of signaling. The community ef-

fect deﬁnition is based on the observation that while

such aggregates usually form around small foci of

cells initially expressing the identity factor of the de-

sired tissue, a certain number of cells capable of ex-

pressing this factor is required within the commu-

nity to achieve stable activation of the whole colony.

It was veriﬁed by dissection experiments, that if the

number of cells is below a certain threshold, the acti-

vation of all cells is unlikely, while above this thresh-

old the activation is prevalent among all cells.

This system can be represented by a simple gene

network with signaling (see Fig. 1) as proposed by

Saka et al. (Saka et al., 2011). It includes the identity

gene g

, which is responsible for production of the

signaling molecule S, which is in turn secreted to the

environment and from there can be sensed by all other

cells via the receptor gene g

capable in turn of acti-

vating the identity gene g

. The whole network forms

a simple positive feedback loop responsible for ampli-

fying the initial signal, while the degradation rate of

the signaling molecule is responsible for the threshold

number of cells required for activation of majority of

cells.

Cell wall

Env

Figure 1: Simple gene regulatory network modeling com-

munity effect.

We have implemented this network in the STOPS

framework and performed one hundred simulations,

consisting of 30 steps each, for different colony sizes

ranging from 50 to 300 cells. Then we measured for

each of the trajectories, how many cells have the iden-

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

336

tity gene (g

) active as a fraction of the whole popula-

tion. For all cases, after 30 generations, we obtained

cell colony either fully activated or fully silent, which

is expected, given the presence of positive feedback

in the system. It was also reassuring to see that the

fraction of simulations leading to a fully activated sys-

tem is exhibiting a stepwise dependence on the colony

size: up to a 100 cells the silent case is clearly dom-

inant, while starting from 150 cells the active state is

dominating the results (see Fig. 2).

Figure 2: Outcomes of simulations of the community effect

model.

3.2 Linear Cell Lineage with

Proliferation

In a study by Lander et al. (Lander et al., 2009)

the authors consider a simple scenario where there

exists a pool of undifferentiated precursor cell pop-

ulation (expressing gene g

) which can then sponta-

neously switch to an intermediate differentiating state

(expressing g

) which then leads to the fully differ-

entiated terminal state (expressing g

). Importantly,

only the undifferentiated states (expressing g

or g

)

can divide, giving rise to new undifferentiated cells,

while the terminally differentiated cells (expressing

) can enter apoptosis (programmed cell death). The

system aims to model neural epithelia which consist

of similar types of cells, which are important for their

ability to quickly recover from removal of large num-

bers of differentiated and intermediate cells, provided

that they are left with enough pluripotent cells. Us-

ing an ODE model for this system, Lander et al. ob-

served that in order to achieve short recovery times

and limited total number of cells it is beneﬁcial to pro-

vide negative feedback from the differentiated cells

instructing the pluripotent cells to limit their growth

rate when the number of differentiated cells is sufﬁ-

cient.

Similar behavior can be observed in a system of

cells modeled with Stochastic Logical Networks fol-

lowing the genetic regulatory interactions depicted in

Figure 3. Each pair of genes representing consec-

Cell wall

Div

Env

Die

Figure 3: Gene network describing cell lineage with prolif-

eration and signaling.

utive cell stages is linked by direct negative feed-

back loop providing basis for cell progression through

the stages. There are two additional variables, cor-

responding to cell death and division and a signal-

ing molecule released by the terminally differentiated

cells and able to limit the proliferation of undifferenti-

ated cells receiving the signal. Gene g

corresponding

to the terminal differentiation is also activating cell

death and repressing proliferation.

To test whether the feedback cycle involving sig-

naling is required for the functioning of the system,

we can consider a system that is identical to the orig-

inal one, but does not include the signaling compo-

nent. Several exemplary trajectories of such a system

are shown in Figure 4. While the general behavior of

the system is consistent with earlier ODE simulations

by Lander and colleagues, it should be noted, that

the slope of recovery of the differentiated cells (blue

lines) is not as steep as it should be and that the re-

quired number of intermediate cells (green line reach-

ing 0.6 of the total population) are not supported by

the experimental data. It is also disturbing to see that

overall the population size is rapidly decreasing as a

result of very quick removal of the primary cells from

the population. It should be noted, that the problems

of the sub-population of proliferating cells extinction

is not visible in the original ODE model, as the pool

of non-differentiated cells can get arbitrarily close to

0 and still be able to regenerate, while our stochastic

model is capable of highlighting problems with mod-

els that lead to depletion of any sub-population as in

our model it is possible to consider parameters lead-

ing to a complete extinction of the system.

If we compare these results to the full model in-

cluding signaling to reduce proliferation when not

needed, we can see clear improvement (see Fig. 4

B). The number of intermediate cells stays below 30

ModelingCellPopulationsinDevelopmentusingIndividualStochasticRegulatoryNetworks

337

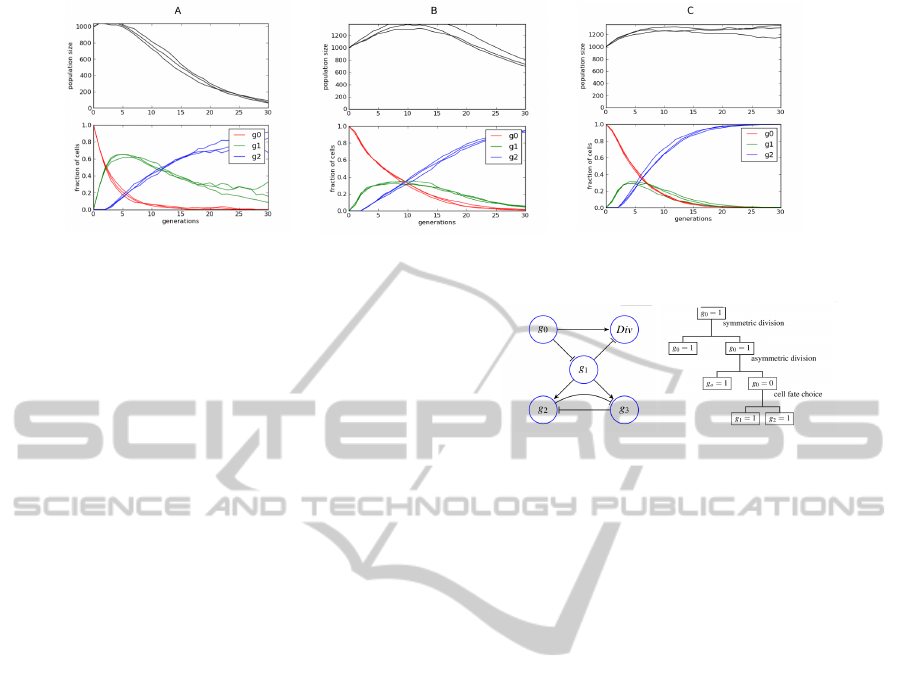
Figure 4: Results of simulation of the cell lineage without feedback (A), with simple feedback (B) and with cell-type speciﬁc

feedback (C).

per cent all the time and the decrease in the number of

primary cells is slower, however the regeneration rate

of the differentiated cells remains unchanged and the

population size problem is only slightly mitigated. So

while it is clear that including feedback in the system

improves the model, it is not sufﬁcient to recapitulate

the experimental results (faster regeneration and sta-

ble population size). It turns out, that the reason for

these problems is the decreasing number of primary

cells and the difﬁculty of the ligand to ﬁnd those cells

before being absorbed by the differentiated cells that

cannot respond to the signal as they are already un-

able to proliferate. This problem cannot be seen in

the ODE model, as there is dependence of the signal

reception by the relative proportion of dividing cells

in the population.

This problem can be eliminated by preventing the

differentiated cells from being able to receive signals

from the environment. Technically this can be done

by including another gene representing the receptor,

which is regulated by g

and which is necessary for

signal reception. Making this change to the system

gives much better results (see Fig. 4 C). Both prob-

lems: slow regeneration rate and population size in-

stability are solved making the model capable of re-

producing experimentally observed behavior.

3.3 Asymmetric Cell Division and

Cell-fate Choice

While signaling is a very powerful mechanism of con-

trolling state changes in developing cells, it is fre-

quently the case that the cell fate choice is determined

by other mechanisms. Cohen et al. (Cohen et al.,

2010) studied recently a system of neural cells dif-

ferentiation, which includes two such mechanisms:

asymmetric cell division and spontaneous stochastic

cell-fate choice based on a bistable system of two

genes.

The asymmetric division is a mechanism in which

a cell expressing a pluripotency factor (in this case

Figure 5: Network model of cell-fate choice with asymmet-

ric cell division and the associated cell lineage tree.

a gene called “numb”) is undergoing an asymmetric

division resulting with one of the daughter cells re-

taining majority of the factor protein, while the other

daughter cell is born free of this protein. This leads

these two cells to reach different regulatory states,

since the pluripotency factor is lost in one of the re-

sulting cells allowing it to start the differentiation pro-

cess. On the regulatory level, the pluripotency factor

is usually a repressor of the differentiation factors. In

case of numb, it represses notch which is responsi-

ble for facilitating speciﬁcation of cells into neurons

(Shen et al., 2002).

The stochastic cell-fate choice facilitated by a

bistable switch is a different regulatory mechanism

which allows cells that already started differentiation

to commit stably to one of the predeﬁned cell-fates.

It is nicely illustrated by the gene regulatory net-

work for Arabidopsis ﬂower development (Espinosa-

Soto et al., 2004), where undifferentiated cells need to

commit to one of the four cell-fates to make all neces-

sary parts of the ﬂower. On the regulatory level, such

system, in its most basic form, consists of an initial

signal: the differentiation factor which drives the ex-

pression of two, mutually exclusive, terminal cell-fate

genes. Both these genes are repressing each other and

repressing the upstream signal leading to the system

with two attractors with either one (and only one) of

the cell-fate genes on.

The system studied by Cohen and colleagues con-

sisted of both those components: ﬁrst it had undif-

ferentiated cells capable of either self-reproduction

by symmetric divisions or performing an asymmetric

division leading to creation of a differentiating cell

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

338

which could then choose one of the two predeﬁned

cell fates. Interestingly, the authors provided exper-

imental measurements of relative number of events

leading to the symmetric vs. asymmetric divisions (53

vs. 19 respectively) and of the relative frequencies of

choosing different cell-fates (10 vs 16). This allowed

us to attempt to build a model capable of reproducing

this behavior using the STOPS framework.

The regulatory network we designed is presented

in Figure 5. It consists of the pluripotency factor g

repressing the differentiation factor g

, which has a

basal expression level driving its expression immedi-

ately upon loss of g

. Naturally, the proliferation fac-

tor activates the capability of cells to proliferate, while

the differentiation gene is shutting this program down

upon activation. The asymmetric division is acting on

the expression level of g

: assuming that the parent

cell had the gene on an asymmetric division results

with two cells which are identical to the parent cell

regarding all genes but g

which will be on in one of

the daughters and off in the other.

Once the differentiation factor g

is turned on, it

starts driving the expression of both cell fate genes,

however it is not necessarily acting on both of them

with the same regulatory inﬂuence. In fact making

those inﬂuences different is essential for reproduc-

ing the correct ratio between the numbers of different

cell-fates in resulting population. At some point, one

of the target gene gets activated subsequently leading

to stable repression of the alternative cell fate. The

overall cell-fate choice diagram is shown in Figure 5

(B).

The results of the simulation are capturing the

general behavior of the system and by choosing the

regulatory inﬂuences carefully, we were able to ob-

tain simulation results matching the experimental re-

sults published by Cohen et al. (Cohen et al., 2010).

4 IMPLEMENTATION AND

PERFORMANCE

BENCHMARKS

The ﬁrst prototype of our stochastic population sim-

ulation (STOPS) method was implemented in pure

python scripting language. While it was convenient

for the prototype, the performance of such a solution

was far from satisfactory. Since this tool is intended

to be used for simulation of cellular populations with

realistic sizes it needs to be able to tackle meaningful

time-scales (thousands of simulation steps) for popu-

lations consisting of millions of cells. As we can see

in Figure 6, the prototype implementation requires be-

tween 10 and 15 minutes for a single simulation step

for a population of 10 million cells.

In order to provide a more efﬁcient platform for

realistic simulations, we have re-implemented the

main algorithm in two different libraries dedicated

to matrix operations: NumPy (Harrington and Gold-

smith, 2009) and pyOpenCL (Kl

ockner et al., 2012).

The ﬁrst one has the advantage of being available on

all major platforms, making it possible for anyone to

install STOPS on their machine and test it with rea-

sonable efﬁciency. The second implementation uses

the OpenCL bindings and allows users equipped with

a machine with a support for an OpenCL implemen-

tation (currently there are OpenCL implementations

released for AMD and Intel CPUs as well as Nvidia

and ATI GPUs) to take advantage of the full poten-

tial of their hardware. We have tested the perfor-

mance of all three implementations on a computer

equipped with an Intel Xeon 3.2Ghz CPU and an

Nvidia Tesla C1070 GPU. It is clear from Figure 6

that while all three implementations taking advantage

of specialized matrix algebra operations outperform

the initial version by an order of magnitude, it should

be noted that the OpenCL version is still an order of

magnitude faster than the NumPy version. Interest-

ingly, the OpenCL performs similarly well both on

CPU and GPU implementations of the OpenCL li-

brary. It is important, as the CPU has typically access

to much larger memory, allowing for simulations of

much larger systems. It should be noted that the mem-

ory consumption is the same (number of cells times

the number of variables times the size of an integer).

Figure 6: Comparison of running times for different STOPS

implementations on three case-study datasets.

5 DISCUSSION AND FUTURE

WORK

We presented here a new approach to modeling cell

populations using stochastic logical networks. It

is particularly well suited for developmental sys-

ModelingCellPopulationsinDevelopmentusingIndividualStochasticRegulatoryNetworks

339

tems, where stochastic behavior of large populations

of proliferating and signaling cells is driven by the

same underlying regulatory machinery encoded in the

genome. We also provide a prototype implementa-

tion capable of simulating cell populations with mil-

lions of cells on a standard personal computer. Even

though the method is rather simple and requires only a

handful of parameters to run a simulation, it is able to

reproduce the results of many more established meth-

ods for wide variety of models relevant for problems

currently under consideration by the modeling com-

munity. In some cases, like the linear cell lineage sys-

tem, it can give us new insights missed by the ODE

model due to its more accurate representation of small

cell populations.

While the results shown are promising, the imple-

mentation is still in an early phase and could greatly

beneﬁt from multiple improvements. One key area

that will work on in the future is extending the model

to take into account spatial aspect of cell populations.

Such functionality would greatly expand the range of

possible applications of this model, however mod-

eling spatially variable signalling without great de-

crease in the method performance poses a consider-

able challenge.

6 AVAILABILITY

The STOPS (STOchastic Population Simulation)

software implementation is publicly available under

the GNU GPL v.2 license. The implementation of all

three case studies is included in current version avail-

able at http://launchpad.net/stops.

ACKNOWLEDGEMENTS

This work was partially supported by the Polish Min-

istry of Science and Education grant number N N301

065236 and by the Foundation for Polish Science

within Homing Plus programme co-ﬁnanced by the

European Union - European Regional Development

Fund.

REFERENCES

Cohen, A., Gomes, F., Roysam, B., and Cayouette, M.

(2010). Computational prediction of neural progen-

itor cell fates. Nature Methods, 7(3):213–218.

De Jong, H. (2002). Modeling and simulation of genetic

regulatory systems: a literature review. Journal of

computational biology, 9(1):67–103.

Espinosa-Soto, C., Padilla-Longoria, P., and Alvarez-

Buylla, E. (2004). A gene regulatory network

model for cell-fate determination during Arabidopsis

thaliana ﬂower development that is robust and recov-

ers experimental gene expression proﬁles. The Plant

Cell Online, 16(11):2923.

Gillespie, D. (1977). Exact stochastic simulation of coupled

chemical reactions. The journal of physical chemistry,

81(25):2340–2361.

Gonzalez, A., Chaouiya, C., and Thieffry, D. (2008). Logi-

cal modelling of the role of the hh pathway in the pat-

terning of the drosophila wing disc. Bioinformatics,

24(16):i234–i240.

Harrington, J. and Goldsmith, D. (2009). Progress report:

Numpy and scipy documentation in 2009. In Varo-

quaux, G., van der Walt, S., and Millman, J., editors,

Proceedings of the 8th Python in Science Conference,

pages 84 – 87, Pasadena, CA USA.

Kauffman, S. (1977). Gene regulation networks: A theory

for their global structure and behaviors. Current topics

in developmental biology, 6:145–182.

ockner, A., Pinto, N., Lee, Y., Catanzaro, B., Ivanov,

P., and Fasih, A. (2012). Pycuda and pyopencl: A

scripting-based approach to gpu run-time code gener-

ation. Parallel Comput., 38(3):157–174.

Lander, A., Gokoffski, K., Wan, F., Nie, Q., and Calof, A.

(2009). Cell lineages and the logic of proliferative

control. PLoS Biology, 7(1):e1000015.

Saka, Y., Lhoussaine, C., Kuttler, C., Ullner, E., and Thiel,

M. (2011). Theoretical basis of the community effect

in development. BMC Systems Biology, 5:54.

anchez, L., Chaouiya, C., and Thieffry, D. (2008). Seg-

menting the ﬂy embryo: logical analysis of the role of

the segment polarity cross-regulatory module. Int. J.

Dev. Biol, 52(8):1059–1075.

Shen, Q., Zhong, W., Jan, Y. N., and Temple, S. (2002).

Asymmetric numb distribution is critical for asym-

metric cell division of mouse cerebral cortical stem

cells and neuroblasts. Development, 129:4843–4853.

Thomas, R. (1978). Logical analysis of systems compris-

ing feedback loops. Journal of Theoretical Biology,

73(4):631–656.

Thomas, R. and D’Ari, R. (1990). Biological feedback.

CRC press.

Wilczynski, B. and Tiuryn, J. (2006). Regulatory network

reconstruction using stochastic logical networks. In

proceedings of the Computational Methods in Systems

Biology 2006, Lecture Notes in Bioinformatics, pages

142–154. Springer Verlag.

Wilczynski, B. and Tiuryn, J. (2007). Reconstruction of

mammalian cell cycle regulatory network from mi-

croarray data using stochastic logical networks. In

proceedings of the Computational Methods in Systems

Biology 2006, Lecture Notes in Bioinformatics, pages

121–135. Springer Verlag.

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

340