A Meta-Model for DEVS

Designed following Model Driven Engineering Specifications

Stéphane Garredu, Evelyne Vittori, Jean-François Santucci and Paul-Antoine Bisgambiglia

SPE-UMR 6134, Università di Corsica, FST Campus Grimaldi, Corte, France

Keywords: DEVS, MDE, MDA, MOF, UML, Meta-modeling, DEVS Interoperability, Model-to-Model

Transformations, Model-to-Text Transformations, OMG MTL.

Abstract: In this paper we give a state-of-art of DEVS components interoperability, and we propose a meta-model for

classic DEVS formalism, designed following a Model-Driven Engineering philosophy. After glancing at the

existing related works, we explain in a step-by-step way how our meta-model is built, starting from the

formal definition of DEVS formalism. As the hardest steps when defining a DEVS Platform-Independent

Model (PIM) are the definition of the states and the definition of the DEVS functions, we particularly focus

on those concepts and we propose a way to describe them in a simple and platform-independent way. UML

class diagrams were chosen to represent this meta-model. Not only can this meta-model be useful to

generate DEVS PIMs but it can also be seen as a powerful tool to improve interoperability between DEVS

models (and in a larger way discrete-event models, via model-to-model transformations) and to provide

automatic code generation towards DEVS simulators (model-to-text transformations). As this meta-model is

not a final version but rather a starting point, we tried to make it as modular and upgradable as possible.

1 INTRODUCTION

For over 30 years now, the Discrete Event system

Specification (DEVS) formalism has been used for

modeling and simulating both discrete-event

dynamic systems (and continuous systems) by a

growing enthusiast community of scientists all over

the world.

Describing a DEVS model in order to perform its

simulation can only be done if we resort to an

Object-Oriented programming Language (OOL),

tied to a particular DEVS simulation platform. Thus,

implementing a DEVS model with an OOL leads to

a loss of comprehensibility, a loss of precision and a

loss of interoperability.

The approach our team has been working on

aims to ease the modeling process and increase the

interoperability of DEVS models. From our point of

view, it can be done if the advantages of Model

Driven Engineering (MDE) methodology are applied

to modeling and simulation. An important part of

this approach is to allow the description of DEVS

models in a unified way, without considering the

platform in which the models will be simulated. To

stick to this philosophy, each DEVS model should

conform to the same pattern. This pattern should

provide all the necessary DEVS concepts in order to

create DEVS models in a unified way: such a pattern

is called a meta-model.

The purpose of this paper is to propose a meta-

model for DEVS. This meta-model is likely to be

enriched with new features: it is designed in a

modular way, and it is upgradable. For read-through

strength reasons, it is shown in this paper with a

well-known and understandable formalism: UML

class diagrams. It also has been fully implemented

within Eclipse Modeling Framework.

This paper starts with the background section:

we present the classic DEVS formalism, DEVS

modeling and simulation philosophy, and DEVS

components interoperability. We say a few words

about UML, MDE (and its particular form Model

Driven Architecture or MDA), we also focus on

related work about DEVS meta-modeling and give a

state-of-art of these approaches. We conclude by a

discussion about this related work. The second part

is dedicated to the process we followed to create our

DEVS meta-model. As much as possible, we try to

stick to the formal definition of DEVS formalism,

and we stress on the particular case of the DEVS

states. We present all the meta-classes involved in

the definition of our meta-model and we stress on

152

Garredu S., Vittori E., Santucci J. and Bisgambiglia P..

A Meta-Model for DEVS - Designed following Model Driven Engineering Speciﬁcations.

DOI: 10.5220/0004061501520157

In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),

pages 152-157

ISBN: 978-989-8565-20-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

the definition of states and functions. Finally, we

give a conclusion.

2 BACKGROUND

2.1 Classic DEVS Formalism

DEVS formalism was introduced in the seventies by

Pr. Zeigler, it is based on discrete events, and it

provides a framework with mathematical concepts

based on the sets theory and systems theory concepts

to describe the structure and the behaviour of a

system (Zeigler, 1989). DEVS knows two kinds of

models: the atomic models, which describe a

behavior, and the coupled models which describe a

hierarchy.

With DEVS, there is an explicit separation

between a model and its simulator: once a model is

defined, it is used to build a simulator (i.e. a device

able to execute the model’s instructions).

Now we present the two DEVS models: atomic

models and coupled models.

2.1.1 DEVS Atomic Models

The tiniest element in DEVS formalism is the

atomic model. It is specified as

AM = < X, Y, S, ta, δ

int

, δ

ext

, λ >

where

- X = {(p,v)|p



InputPorts, vX

} is the input events

set, through which external events are received;

InputPorts is the set of input ports and X

is the set

of possible values for those input ports

- Y = {(p,v)|p



OutputPorts, vY

} is the output

events set, through which external events are sent;

OutputPorts is the set of output ports and X

is the

set of possible values for those output ports

- S is the states set of the system;

- ta: S → R

 +∞ is the time advance function (or

lifespan of a state);

- δ

int

: S → S is the internal transition function;

- δ

ext

: Q × X → S with Q = {(s,e)/sS, e[0,ta(s)]} is

the external transition function;

- λ: S → Y, with Y = {(p,v)|p



OutputPorts, vY

} is

the output function;

The simplest transition is called the internal

transition, it behaves as follows: at a given moment,

a system is in a state sS. Unless an external event

occurs on an input port, the system remains in the s

state for a duration defined by ta(s). When ta(s)

expires, the model sends the value defined by λ(s) on

an output port y

Y

, and then it changes to a new

state defined by δ

int

(s). Such a transition, which

occurs because of the expiration of ta(s), is an

internal transition.

The other transition type is called the external

transition, because it is triggered by an external

event. In this case, it is the δ

ext

(s,e,x) function which

defines which state is the next one (s is the current

state, e is the elapsed time since the last transition,

and xX

is the event received).

In both cases, the system is now in a new state s’

for a new duration d’ = ta(s’) and the algorithm

restarts.

ext

int

Figure 1: A DEVS atomic model.

2.1.2 DEVS Coupled Models

A coupled model is composed of at least one

submodel (atomic or coupled). It is formally defined

MC = <X, Y, D, {Md|d



D}, EIC, EOC, IC, select>

Where

- X = {(p,v)|p



InputPorts, vX

} is the input events

set, through which external events are received;

InputPorts is the set of input ports and X

is the set

of possible values for those input ports

- Y = {(p,v)|p



OutputPorts, vY

} is the output

events set, through which external events are sent;

OutputPorts is the set of output ports and X

is the

set of possible values for those output ports

- D is the set of component names, d





- M

is a DEVS model (either atomic or coupled)

- EIC is the set of external input couplings;

- EOC is the set of external output couplings;

- IC is the set of internal couplings;

- select is the tiebreaker function

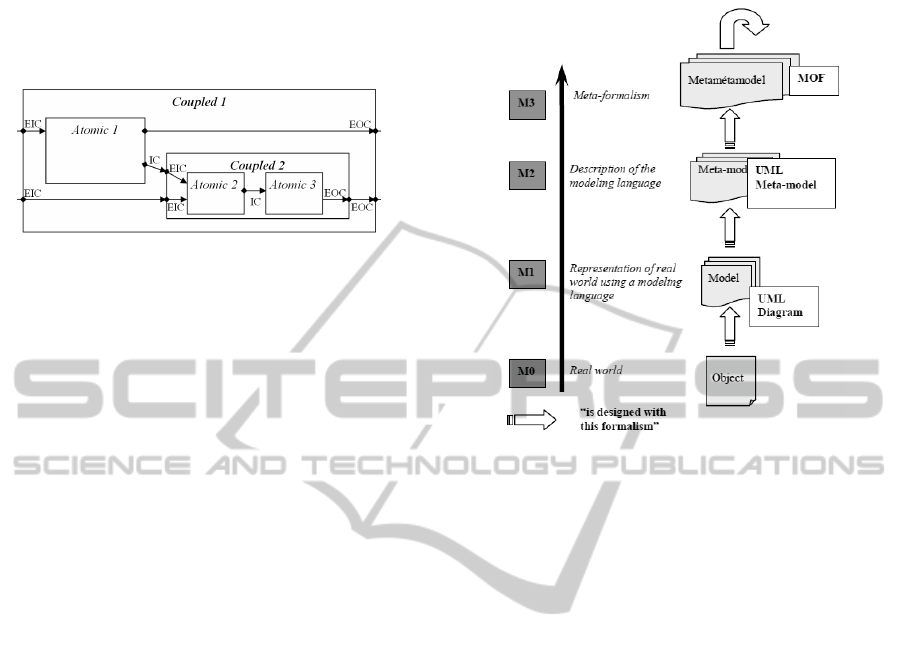
Figure 2 illustrates an example of a coupled model.

2.1.3 DEVS Simulators

Several simulators for DEVS have been

implemented.

They are built with various OOL languages and

even for those which use the same language, the

simulations algorithms are different. Among them

AMeta-ModelforDEVS-DesignedfollowingModelDrivenEngineeringSpecifications

153

we can quote CD++ (Wainer, 2002), a framework

which uses C++, JDEVS (Filippi et al., 2004) and

DEVSJAVA (ACIMS 2012) which both use JAVA,

PythonDEVS (Bolduc et al., 2002) which is written

in Python.

Figure 2: A DEVS coupled model.

2.1.4 DEVS Components Interoperability

The fact of implementing a DEVS model highly

reduces its interoperability.

To solve this, two major kinds of solutions have

been used. The first one aims to increase the

interoperability in a model-centered way, while the

second one aims to increase the interoperability from

the simulator’s point of view, using standard

messages between at least two different simulation

platforms where different models are defined. For

instance, (Seo, 2009) is a simulator-oriented

proposal for a better DEVS simulators

interoperability using SOA.

An exhaustive overview of all those different

solutions is presented in (Touraille et al., 2009).

As our approach is part of the first kind of

solutions, we will only focus on the existing work

which belongs to DEVS models interoperability.

2.2 Software Engineering Background

2.2.1 UML

Unified Modeling Language (UML) is a graphical

set of modeling formalisms: it provides a toolkit

which enables one to model the structural aspects of

a system as well as its behavior (Booch et al., 1998).

UML is owned by the Object Management

Group, and its current version is UML 2.4.1 (OMG,

2011). Its main advantage is that it is considered as a

standard formalism by a large worldwide

community of users.

2.2.2 UML and Meta-Levels

A UML model, for instance a UML class diagram, is

an abstraction of a system from the real world

located at the lowest abstraction level: M0. Such an

abstraction takes place at a higher level: M1. It is

defined by its meta-model at, once more, a higher

level: M2.

Figure 3: UML and the “meta” levels.

This meta-model describes the elements that can be

used to design the model and their relationships with

each other. Such a description is defined at a higher

level by Meta Object Facility (MOF), a language

used to describe other languages. This level is M3.

MOF is defined on itself, i.e. it is described in MOF

terms. Hence, there is no level higher than M3

(Figure 3).

2.2.3 MDE and MDA

Model Driven Engineering is a software

development methodology which focuses on

creating and exploiting domain models. MDE is a

generic approach, and its most famous

implementation is Model Driven Architecture,

owned by the OMG.

MDA (Model Driven Architecture) (OMG,

2001) is a software design approach initiated by the

OMG in 2001 to introduce a new way of

development based upon models rather than code.

MDA defines a set of guidelines for defining

models at different abstraction levels, starting from

Computational Independent Models (CIMs) to

platform independent models (PIMs), then from

PIMs to platform specific models (PSMs) which are

tied to a particular technology (i.e. platform). The

translation from one PIM to one or several PSMs is

to be performed automatically by using

transformation tools. MDA also enables

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

154

transforming a PSM into source code. The

advantage of such an approach is the great

reusability of models.

OMG provides a set of standards dedicated to

this approach. Although UML was at the beginning

the basis of the OMG works on MDA, it is now

Meta-Object Facility (MOF) which appears to be the

most basic standard. The MOF equivalent in EMF is

Ecore.

2.3 Work related to DEVS

Meta-Modeling

A DEVS meta-model must allow the description of

DEVS atomic and coupled PIMs in terms of DEVS

formalism. The related work about DEVS meta-

modeling can be characterized by the formalism

used to define the meta-model.

Many approaches use XML to specify the DEVS

basic elements, such as (Mittal et al., 2007) which

can be considered as a “hybrid” approach as it uses

SOA in order to perform the simulation. DTDs are

used to describe the structure of a DEVS component.

A DEVS framework named SimStudio uses a

similar specification language named DML

(Touraille et al., 2010). It also has its own simulation

engine called DEVS-MS. In this approach, the XML

schema (and not the DTD) gives the structure of a

DEVS component.

A DEVS meta-model was also specified using

Entity-Relationship diagrams, the meta-meta-

formalism used by AToM

(Posse et al., 2003).

The main difficulty that remains is to specify the

behaviour of the models: to do so, the previous

approaches often use object-oriented code (with a

loss of the platform-independent aspect) or hybrid

code (a mix between generic code and object-

oriented code.

3 A META-MODEL FOR DEVS

The goal of our approach is to make a proposal for a

DEVS meta-model. In order to be fully compliant

with MDE and in particular MDA philosophy, all

the models generated from this single entry point are

platform-independent. We chose UML class-

diagrams to represent the meta-classes of our meta-

model, and we implemented it within EMF. The

theoretical aspects of our approach are presented in a

more detailed way in (Garredu et al., 2011).

3.1.1 Basic Hierarchy

Every DEVS model must be given a name.

Moreover, it can either be atomic or coupled. As a

consequence, there must exist an abstract meta-class

DEVSModel from which two sub-classes

(AtomicDEVS and CoupledDEVS) inherit. A

coupled DEVS model contains at least one DEVS

model. Such a basic hierarchy will be refined and

presented in the DEVSModel package.

3.1.2 Dealing with Types

Types are defined differently following the object-

oriented languages. So, our meta-model must be able

to handle types, in a generic way. Types will be

useful. We chose to represent only 4 basic types

(StringType, IntegerType, CharType, BooleanType)

but this can be easily extended. The types inherit

from the Type abstract meta-class.

3.1.3 Representing the States

In a formal point of view, a DEVS atomic model is

composed of a finite set of its possible states S

linked by deterministic transitions. Those states are

distinct values; it implies that the fact of changing a

state may lead to the creation of another state.

This is not a problem for the systems of which

the states are known (and can be enumerated) but it

becomes one when we have to deal with states

which take their values in infinite sets, for instance

[0;1]R.

To solve this problem, we chose to represent a

state by what we call a state variable. It takes a new

value when the state changes (i.e. each new state

change will lead to a change of the value of the state

variable).

Therefore, only a state variable is used to

represent a collection of states which belong to the

“same kind”. A state variable must be named, and

must be typed. It can also be affected a literal value.

3.1.4 The Ports

Each port must be named, and also must be typed in

order to send or receive information. A port can be

an input port, or an output port. Port is an abstract

meta-class from which inherit the two meta-classes

InputPort and OutputPort.

3.1.5 The Coupling Functions

Once we know how to represent a port, we easily

can write the meta-classes which describe the

coupling functions (in the coupled models). Some

AMeta-ModelforDEVS-DesignedfollowingModelDrivenEngineeringSpecifications

155

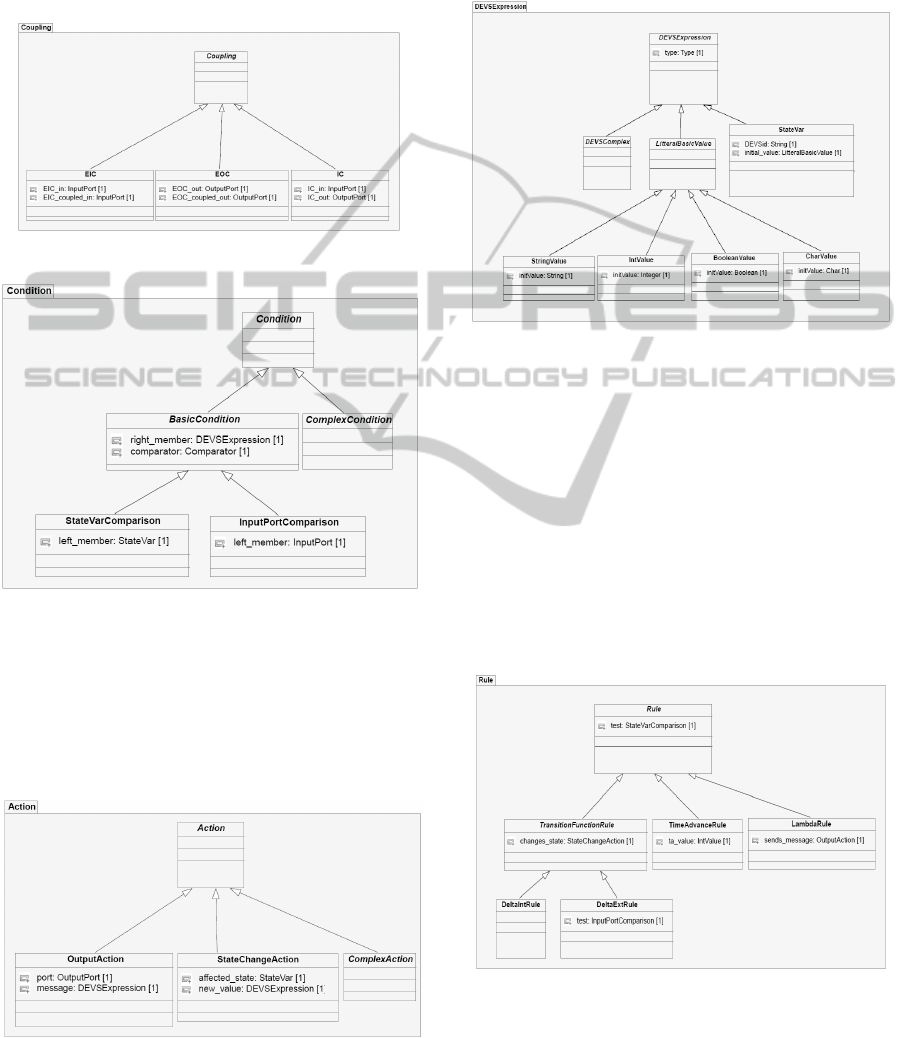
information cannot be directly specified here (for

instance, the fact that EIC involves 2 sub-models)

but it can be using OCL constraints. Figure 4

represents the Coupling package. As usual, there is

an abstract class (Coupling) from which inherit 3

sub-classes: EIC, EOC, IC.

Figure 4: The Coupling package.

Figure 5: The Condition package.

A condition (see Figure 5) is described by a test: a

left member, a comparator, and a right member.

It can be a test on an input port (in the case of an

external transition function) or on a state variable (in

every DEVS atomic function, there is a test on a

state variable).

Figure 6: The Action package.

An action (figure 6), in fact the description of an

action, can be an output action (on a port), or a state

change action (in the case of a transition function).

3.1.6 DEVS Expressions

Figure 7: The DEVSExpression package.

We chose to describe state variables and types, and

they can be included in a larger set which is called

DEVSExpression. It is one of the basis of our meta-

model. As a StateVar is a DEVSExpression, a

LitteralBasicValue is also a simpler one, in fact the

simplest one because it is composed of a unique

typed value. We built this package (see Figure 7) in

a modular way, in order to facilitate its modification

by enriching it with other sub-classes.

DEVSComplex is a good starting point to do so.

3.1.7 DEVS Rules

Figure 8: The Rule package.

In spite of the differences between the DEVS

functions, we can notice that every function can

describe a test, an action on a variable, a message.

Those descriptions follow a sort of pattern which is

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

156

often the same: a set of enumerations. Those

enumerations are DEVS Rules. The purpose of a rule

is to represent a set of operations on specific

elements.

A rule is always composed of a condition and an

action. The Rules package (Figure 8) purpose is to

enable the description of simple rules often used in

DEVS atomic models. We finally present the core of

our meta-model, the DEVS-Models package (Figure

9). It takes into account all we said before, putting

all together.

Figure 9: The DEVSModel package.

4 CONCLUSIONS

We presented in this paper a state-of-art about

DEVS models interoperability and proposed the first

fully platform-independent meta-model for DEVS

formalism. Although this meta-model only allows

specifying simple functions, it is consistent with

classical DEVS formalism.

This meta-model has been implemented within

the Eclipse Modeling Framework and used in a

MDA approach to perform code generation. Models

were designed in EMF, then with Model-To-Text

transformations, Python code was generated. This

will be presented in another paper.

The meta-model’s modular features will help us

to improve it; the next step in our work is the

definition of complex expressions.

RFERENCES

ACIMS, DEVSJAVA, http://www.acims.arizona.edu,2012

J.-S. Bolduc and H. Vangheluwe, A modeling and

simulation package for classic hierarchical DEVS.

Internal document for the Modelling, Simulation and

Design Lab (MSDL), School of Computer Science,

McGill University, 2002.

G. Booch, J. Rumbaugh, and I. Jacobson. “The unified

Modeling Language User Guide”. Addison-Wesley,

1998.

J.-B. Filippi and P. Bisgambiglia, JDEVS: “An

implementation of a DEVS based on formal

framework for environmental modelling” Original

Research Article Environmental Modelling &

vSoftware, Volume 19, Issue 3, March 2004, Pages

261-274

S. Garredu, E. Vittori, J.-F. Santucci, D. Urbani, “A

methodology to specify DEVS domain specific

profiles and create profile-based models”, IEEE-IRI

2011, 3-5 Aug. 2011, Las Vegas, NV, U.S.A., pp. 353 -

359

S. Mittal, J. L. R. Martín., B.P. Zeigler « DEVSML:

automating DEVS execution over SOA towards

transparent simulators », Proceedings of the 2007

ACM Spring Simulation Multiconference, March 25-

29, 2007, Norfolk, VA, USA, Vol. 2, pp. 287-295.

OMG 2011. Unified Modeling Language: Superstructure

and infrastructure, version 2.4.1, August 2011

http://www.omg.org/spec/UML/2.4.1/

OMG 2001. Model Driven Architecture homepage

http://www.omg.org/mda/

Posse E., Bolduc J.-S., « Generation of DEVS Modelling

& Simulation Environments », Proceedings of the

2003 SCS Summer Computer Simulation Conference,

July 2003, Montréal, Canada, pp. 295-300.

C. Seo, "Interoperability between DEVS Simulators using

Service Oriented Architecture and DEVS

Namespace", Ph.D. Dissertation, Electrical and

Computer Engineering Dept., University of Arizona,

Spring 2009

L.Touraille, M. K. Traoré, D. Hill, "On the interoperability

of DEVS components: On-Line vs. Off-Line

Strategies.", 2009, UMR CNRS 6158, LIMOS/RR-09-

04, 13 p.

L.Touraille, M.K. Traoré, D. Hill, « SimStudio : une

Infrastructure pour la Modélisation, la Simulation et

l’Analyse de Systèmes Dynamiques Complexes »,

UMR CNRS 6158, LIMOS/RR-10-13, 2010, 12 p.

(2010)

G. Wainer, “CD++: a toolkit to define discrete event

models”. Software, Practice and Experience. Vol.32,

No.3. pp. 1261-1306. November 2002

B.P. Zeigler, 1989. "DEVS Representation of Dynamical

System", in Proceedings of the IEEE, Vol.77, pp.72-80

AMeta-ModelforDEVS-DesignedfollowingModelDrivenEngineeringSpecifications

157