
Behavior Analysis of a Gaussian Beam Optical Trap
in the Rayleigh Regime
Niazul Islam Khan, A. S. M. Abdul Hye, M. D. Rejwanur R. Mojumdar and S. K. Shaid-Ur Rahman
Faculty of Engineering and Computer Science, Ulm University, Albert-Einstein-Allee, D-89069 Ulm, Germany
Keywords:
Optical Trapping, Rayleigh Regime, Lorentz Force, Scattering Force, Gradient Force, Optical Tweezers.
Abstract:
Recently optical trapping has emerged as a very powerful tool for manipulating micro and nanometer sized
particles. In this paper, we present a comprehensive study of the behavior of nanometer sized trapped particles
in a Gaussian beam optical trap using Rayleigh model of trapping forces. Along with the working principle
of an optical trap, the force equations in the Rayleigh regime have been derived considering focused Gaussian
beam. Then numerical simulations are performed for a 30 nm particle with refractive index 1.57 considering
water as the surrounding medium. We assume that the wavelength of the light source to be 850 nm easily
obtainable from cheap GaAs-based vertical-cavity surface-emitting laser technology. When the light hits a
particle, it influences the particle with two forces–the scattering force in the direction of propagation and the
gradient force in the direction of gradient of light intensity. We explore the effects of particle size, refractive
index of the particle, beam waist radius, position of the particle with respect to the trap center both on scattering
and gradient forces. This analysis will be helpful for understanding optical manipulation of nanoparticles and
designing suitable trap modules for nanoparticle manipulation.
1 INTRODUCTION
Today the world-wide research deals with nanometer
and micrometer sized particles in different field of sci-
ences like physics, chemistry or biology. To manipu-
late or handle these tiny particles, an effective method
had been in a demand. Optical manipulation can serve
this purpose without any mechanical damage or con-
tamination, as no physical contact is required here. It
is based on the optical trapping phenomenon. To de-
scribe the trapping force, we consider three scattering
regimes based on the size of the particle under consid-
eration. The three regimes are given in Table 1, where
λ is the wavelength and d is the particle diameter.
2 WORKING PRINCIPLE OF AN
OPTICAL TRAP
The working principle of an optical trap is based on
the light-matter interaction. We know that the light
has a momentum p, which is given by
p = h/λ, (1)
where h is the Planck’s constant and λ is the wave-
length of light. When the light hits a dielectric parti-
cle, there is a change of the momentum of the particle
due to momentum transfer between the particle and
the light. The rate of change of momentum gives rise
to a force on the particle. This force can be decom-
posed into two components– (i) the scattering force in
the direction of light propagation and (ii) the gradient
force in the direction of the spatial intensity gradient.
Fig. 1 shows the working principle of an optical trap.
Suppose, a dielectric transparent sphere with several
wavelengths of diameter and refractive index higher
than that of the surrounding medium is located off-
axis in an unfocused Gaussian beam. We consider
two parallel rays labeled A and B of the beam hitting
the sphere near the center. Ray A has greater intensity
than ray B. When these rays hit the sphere, two opti-
cal phenomena happen– reflections and refractions at
the interfaces of the sphere and surrounding medium.
If we take only the refractions into account, these two
rays will be refracted as they enter and exit the sphere.
The exit rays are in the directions different from their
original directions, which means a change of momen-
tum of the incident rays. According to Newton’s third
law of motion, there must be an equal change of mo-
mentum of the sphere in the opposite direction. The
rate of change of momentum gives rise to two forces
F
A
and F
B
on the sphere that are in a direction perpen-
365
Islam Khan N., S. M. Abdul Hye A., D. Rejwanur Rashid Mojumdar M. and K. Shaid-Ur Rahman S..
Behavior Analysis of a Gaussian Beam Optical Trap in the Rayleigh Regime.
DOI: 10.5220/0004063803650370
In Proceedings of the International Conference on Data Communication Networking, e-Business and Optical Communication Systems (OPTICS-2012),
pages 365-370
ISBN: 978-989-8565-23-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
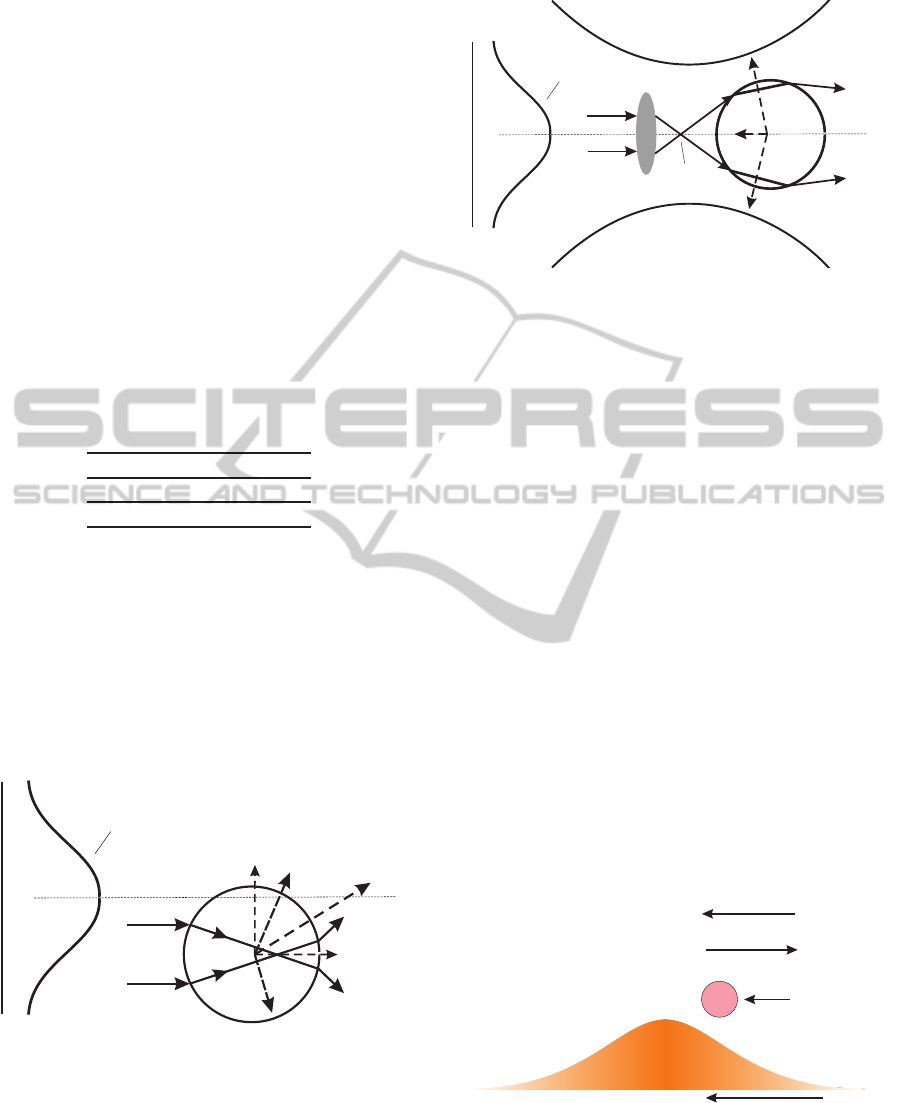
dicular to the direction of the respective ray and these
forces act at the center of the sphere. As the intensity
of ray A is stronger than that of ray B, F
A
is larger than
F
B
, which pulls the sphere toward the light intensity
maximum. Considering all such symmetric pairs of
rays incident on the sphere, we find that the net force
F
net
can be resolved into two components: scattering
force, F
scatt
pointing to axial direction of light beam
and the transverse gradient force F
grad,tr
pointing to
the radial direction of the beam. For a sphere located
on-axis or in a plane wave, F
A
= F
B
and there is no net
transverse force component, the sphere does not move
in the transverse direction. But the axial component,
which is the scattering force pushes the sphere in the
forward direction.
Fig. 2 shows a three-dimensional optical trap, also
Table 1: Different optical scattering regimes based on the
size of the particle.
d ≪ λ Rayleigh regime
d ≈ λ Mie regime
d ≫ λ Ray optics regime
known as optical tweezers. With a high numerical-
aperture objective, the Gaussian beam is focused re-
sulting an intensity gradient in the axial direction. The
net axial gradient force F
grad,ax
pulls the sphere to-
wards the focus. If reflection of light is considered,
there will be scattering force that pushes the sphere
in the forward direction. The sphere will be stably
trapped, if the net axial gradient force F
grad,ax
com-
pensates the scattering force.
A
B
F
A
F
B
Gaussian beam
Transverse intensity gradient
F
scatt
F
grad,tr
F
net
Figure 1: Illustration of scattering and gradient force of an
optical trap considering only the refracted beams. The re-
fraction of two rays A and B results in two forces namely
F
A
and F
B
. The resultant force F
net
can be resolved into
two perpendicular components: F
scatt
in the longitudinal di-
rection and F
grad,tr
in the transverse direction. F
scatt
pushes
the sphere int the direction of light propagation and the
F
grad,tr
pulls the sphere toward the maximum light intensity;
adapted from (Ashkin, 1997).
A
B
F
A
B
F
A
F
B
Gaussian beam
focus
Longitudinal intensity gradient
Transverse intensity gradient
grad,ax
Figure 2: Schematic of a three-dimensional optical trap.
The laser light is focused by a high numerical-aperture ob-
jective. The axial components of F
A
and F
B
add to each
other and pulls thesphere towards the focus forming a three-
dimensional trap.
3 DESCRIPTION OF TRAPPING
FORCES IN THE RAYLEIGH
REGIME
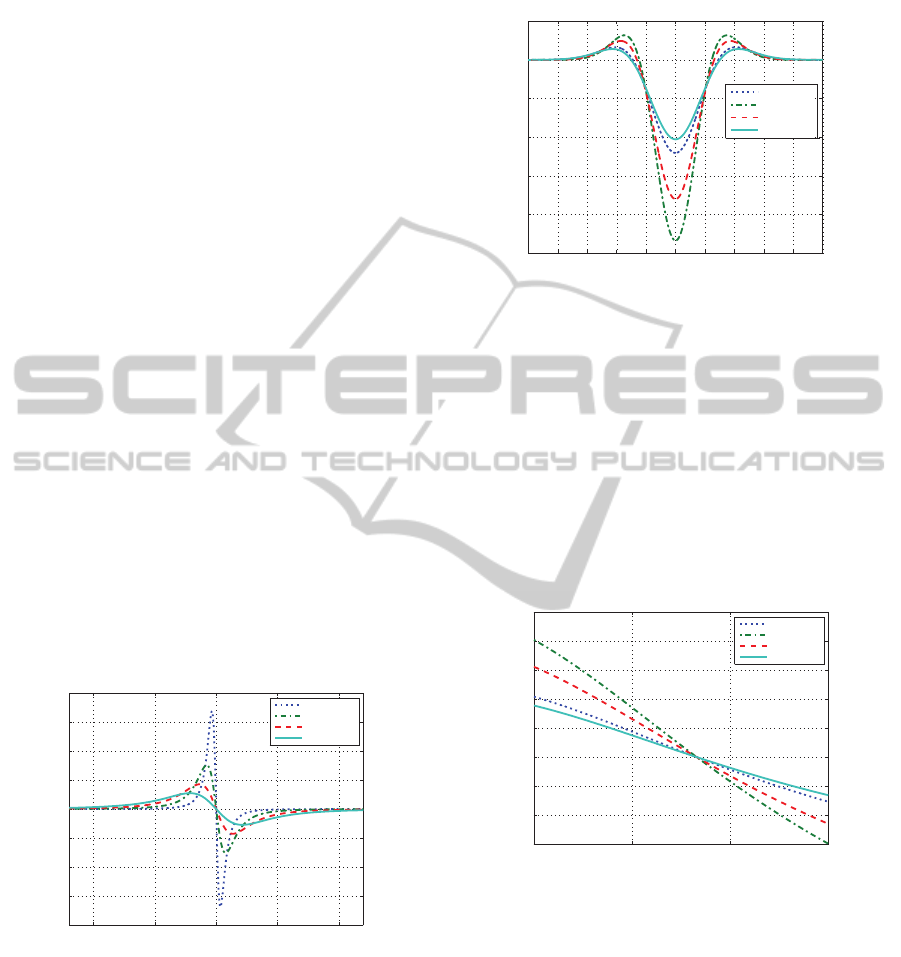
In the Rayleigh regime, the particle can be treated as
an electric point dipole. As a result, we need to con-
sider the polarizability of the dipole. However, in this
regime scattering force is generated by the change
of momentum of light due to scattering of light by
the particle and the gradient force is generated by the
Lorentz force acting on the induced dipole (Malagino
et al., 2002). The direction of the Lorentz force is in
the direction of the intensity gradient of light. Fig. 3
illustrates gradient force in the Rayleigh regime. The
particle is shown as a dipole. The force direction is
along the gradient direction of electric field and par-
ticle moves towards the highest intensity of the light
beam. For a particle of radius a, the scattering force
Light intensity gradient
Lorentz force
Electric field
+
-
Particle
Figure 3: Schematic illustration of the transverse force
in the Rayleigh regime, where dielectric particles can be
treated as perfect dipoles. The Lorentz force caused by the
gradient of light intensity attracts the particle towards the
maximum intensity of the beam; adapted from (Schaevitz,
2006).
OPTICS2012-InternationalConferenceonOpticalCommunicationSystems
366

and gradient force is given by Neuman et al. (Neuman
and Block, 2004)
F
scatt
=
Iσn
m
c
, (2)
with
σ =
128π
5
a
6
3λ
4
m
2
− 1
m
2
+ 2
2
, (3)
where I is the intensity of the incident light, σ is the
scattering cross section of the particle, n
m
is the index
of refraction of the medium, c is the speed of the light
in vacuum, m is the effective refractive index defined
as the ratio of the index of refraction of the particle to
the index of refraction of the medium (n
p
/n
m
), and λ
is the wavelength.
The gradient force is expressed as
F
grad
=
2πα
cn
m
2
∇I, (4)
where α is the polarizability of the sphere and ex-
pressed as
α = n
m
2
a
3
m
2
− 1
m
2
+ 2
. (5)
As the gradient force is caused by the Lorentz force,
it always acts in the direction of gradient of intensity
of the light as seen in Fig. 3.
4 MODELING OF TRAPPING
FORCE FOR A GAUSSIAN
BEAM OPTICAL TRAP
We consider a focused Gaussian beam as the three-
dimensional optical trap with following intensity dis-
tribution as seen in Fig. 4
I(r,z) = I
0
w
0
w(z)
2
exp
−2r
2
w
2
(z)
, (6)
with
w(z) = w
0
s
1+
z
z
r
2
, (7)
where I
0
is the intensity of light at the beam center,
r =
p
x
2
+ y
2
is the radial distance from the center
axis of the beam or the so-called beam-axis, z is the
axial distance from the beam center, w(z) is the spot
size as a function of z and the beam waist w
0
= w(z)
at z = 0. z
r
is the Rayleigh length and is given by
z
r
=
πw
0
2
λ
. (8)
A particle of radius a (a ≪ λ) is located at z = z
1
,
x = x
1
and y = 0 as in Fig. 4. The particle will ex-
perience the following forces: (i) the scattering force
along +z direction (F
scatt
), (ii) the gradient force along
+x direction (F
grad,tr
) and (iii) the gradient force along
−z direction (F
grad,ax
). As y = 0, there will be no gra-
dient force component along y direction. F
scatt
is di-
rectly given by Eq. (2). To get the other two gradient
forces we refer to Eq. (4), which can be written as
F
grad
=
2πα
cn
m
2
i
∂
∂x
+ j
∂
∂y
+ k
∂
∂z
I, (9)
where i, j and k are the unit vectors along the x, y and
z axes, respectively. From Eq. (9), we can write
F
grad
= iF
x,grad
+ jF
y,grad
+ kF
z,grad
, (10)
where
F
x,grad
= F
x,grad,tr
=
2πα
cn
m
2
∂I
∂x
, (11)
F
y,grad
= F
y,grad,tr
=
2πα
cn
m
2
∂I
∂y
, (12)
F
z,grad
= F
grad,ax
=
2πα
cn
m
2
∂I
∂z
. (13)
In this case F
y,grad
= 0. However, after some calcula-
tions we reach the magnitudes of the gradient forces
as
F
grad,tr
= F
x,grad
= −I
0
2πα
cn
m
2
4w
0
2
x
w
4
(z)
exp
−2x
2
w
2
(z)
,
(14)
and
(15)
F
grad,ax
= −I
0
2πα
cn
m
2
2w
0
2
z
w
2
(z)
exp
−2x
2
w
2
(z)
−
4x
2
w
0
2
z
w
3
(z)
exp
−2x
2
w
2
(z)
.
w
0
w(
z)
z
x
y
F
scatt
F
grad,tr
F
grad,ax
Beam waist
Beam center
Particle
Figure 4: Modeling of trapping force exerted on particle
located in a focused Gaussian beam in the Rayleigh regime.
BehaviorAnalysisofaGaussianBeamOpticalTrapintheRayleighRegime
367
5 SIMULATION RESULTS AND
DISCUSSIONS
In this section, we present the simulation results for
the particle located in the optical trap in the Rayleigh
regime as shown in Fig. 4. The simulations are done
for a particle with refractive index of 1.57 with water
as the surrounding medium (n
m
= 1.33). The diam-
eter of the particle is 30 nm. Also, the effects of dif-
ferent beam waist radii of 40nm, 60 nm, 80 nm and
100 nm were observed. A focused Gaussian beam is
assumed as the optical trap. Here the beam-axis is the
z-axis. The simulation results, along with discussions
are presented below for the forces, which are experi-
enced by the particle.
5.1 Axial Gradient Force
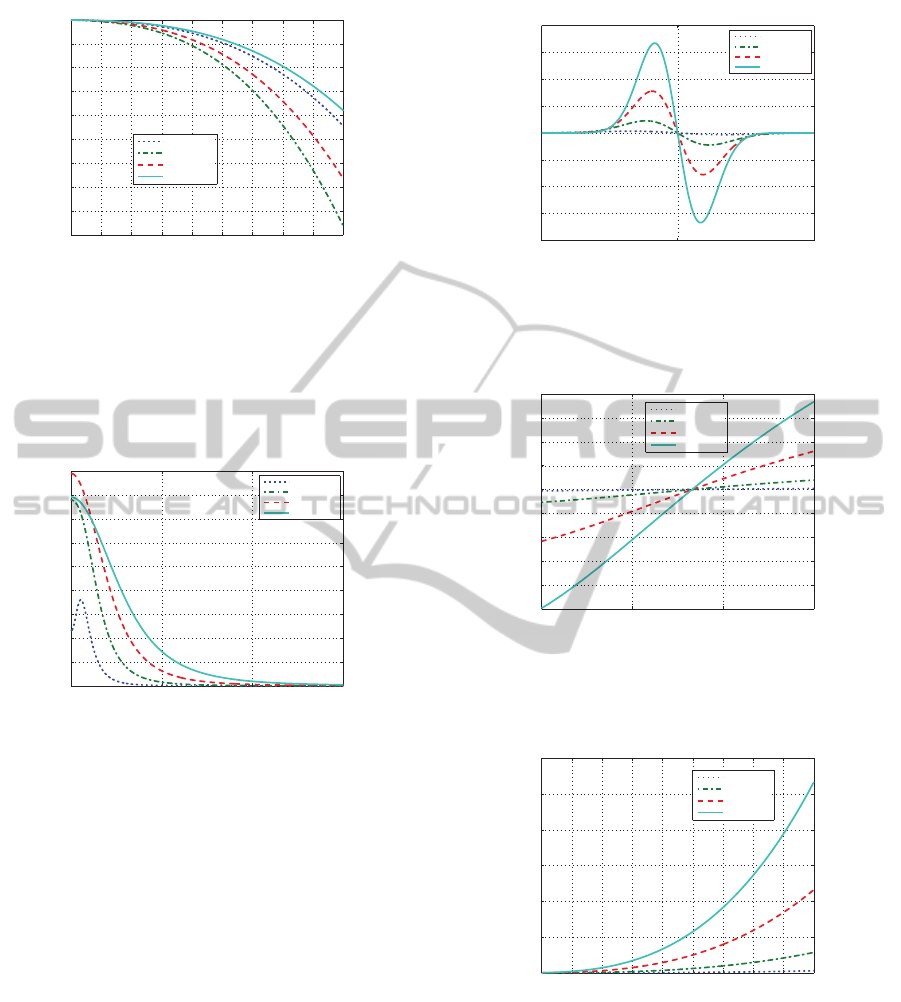
Fig. 5 shows the dependence of axial gradient force
as a function of the axial distance of the particle from
the beam center. When the particle is located at left
side of the beam center, it experiences a force towards
the beam center along the positive z-axis indicated by
the positive magnitude of force at the left of the ori-
gin. On the other hand, if the particle is located at the
right side of the bean center, it experiences the force
along the negative z-axis. The effect of beam waist
radius is also observed. Very close to the beam cen-
ter, the less the beam waist radius, the more the axial
gradient force. Fig. 6 depicts the effect of transverse
-100 -50 0 50 100
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
x 10
-5
Axial distance of particle along z-axis (nm)
Axial gradient force (arb. unit)
w0= 40 nm
w0= 60 nm
w0= 80 nm
w0= 100 nm
Figure 5: Axial gradient force versus axial distance z of the
particle located at x = 0, y = 0 from the beam center for
different beam waist radii.
distance from the beam-axis on axial gradient force.
It is observed that the maximum axial gradient force
which acts along the negative z-axis occurs when it is
located on the beam-axis. In this case, we get highest
axial gradient force at a beam waist radius of 60nm.
This is because, at z = 14 nm the axial gradient force
is highest in magnitude for 60 nm beam waist radius
as seen in Fig. 5. Axial gradient force versus refrac-
-250 -200 -150 -100 -50 0 50 100 150 200 250
-2.5
-2
-1.5
-1
-0.5
0
0.5
x 10
-6
Transverse distance of particle from z-axis (nm)
Axial gradient force (arb. unit)
w0= 40 nm
w0= 60 nm
w0= 80 nm
w0= 100 nm
Figure 6: Axial gradient force versus transverse distance x
of the particle located at y = 0, z = 14 nm from the beam-
axis for different beam waist radii.
tive index of particle is plotted in Fig. 7. The force
direction depends on the effective refractive index m
of the particle. The trap pulls the particle towards the
beam center, if its refractive index is more than the re-
fractive index of its surrounding medium (m > 1) and
vice versa if its refractive index is less than that of
its surrounding medium (m < 1). Highest axial gra-
dient force occurs at 60 nm beam waist radius. From
0.5 1 1.5 2
-6
-4
-2
0
2
4
6
8
10
x 10
-6
Refractive index of particle
Axial gradient force (arb. unit)
w0= 40 nm
w0= 60 nm
w0= 80 nm
w0= 100 nm
Figure 7: Axial gradient force versus refractive index of
particle located at x = 0, y = 0, z = 14 nm for different beam
waist radii.
Fig. 8, it is clearly visible that the axial gradient force
increases in magnitude with increase in the radius of
particle because of the increasing overlap between the
optical field and the particle.
5.2 Transverse Gradient Force
Fig. 9 shows the dependence of transverse gradient
force on the axial distance of the particle from the
beam center. Positive forces indicate that the force
OPTICS2012-InternationalConferenceonOpticalCommunicationSystems
368
10 20 30 40 50 60 70 80 90 100
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
x 10
-5
Radius of particle (nm)
Axial gradient force (arb. unit)
w0= 40 nm
w0= 60 nm
w0= 80 nm
w0= 100 nm
Figure 8: Axial gradient force versus radius of the particle
located at x = 0, y = 0, z = 14 nm for different beam waist
radii.
direction is towards the positive x-axis in Fig. 4. As
a result the particle is pulled towards the beam-axis
where the light intensity is the highest. Form Fig.
0 50 100 150
0
1
2
3
4
5
6
7
8
9
x 10
-7
Axial distance along z-axis (nm)
Transverse gradient force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 9: Transverse gradient force versus axial distance z
of the particle located at x = −54 nm, y = 0 from the beam
center for different beam waist radii.
10, the dependence of transverse gradient force on the
transverse distance of the particle from z-axis can be
seen. When the particle is located on the beam-axis, it
experiences no forces. But when it moves away from
the beam-axis, it experiences a force which pulls it
back towards the beam-axis. On both sides, at a cer-
tain distance from the beam-axis, this force becomes
maximum. The behavior of transverse gradient force
with respect to refractive index of particle and particle
radius is same as the behavior of axial gradient force,
except the force directions indicated by the force mag-
nitudes as seen in Figs. 11 and 12.
5.3 Scattering Force
Fig. 13 shows that, unlike Fig. 5, the scattering force
is always positive for any axial position of the particle
with respect to the beam center. That means, scatter-
ing force always pushes the particle away from the
-500 0 500
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
x 10
-7
Transverse distance of particle from z-axis (nm)
Transverse gradient force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 10: Transverse gradient force versus transverse dis-
tance x of the particle from z-axis at y = 0, z = 14nm for
different beam waist radii.
0.5 1 1.5 2
-5
-4
-3
-2
-1
0
1
2
3
4
x 10
-7
Refractive index of particle
Transverse gradient force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 11: Transverse gradient force versus refractive index
of the particle located at x = −54 nm, y = 0, and z = 14 nm
for different beam waist radii.
10 20 30 40 50 60 70 80 90 100
0
1
2
3
4
5
6
x 10
-6
Radius of particle (nm)
Transverse gradient force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 12: Transverse gradient force versus radius of the
particle located at x = −54 nm, y = 0, and z = 14 nm beam
waist radius.
beam center towards the forward direction. Fig. 14
tells that when the particle is located on the beam-
axis, it experiences the highest scattering force. Also
in contrast to Fig. 7, Fig. 15 shows that the direc-
tion of scattering force does not depend on the effec-
tive refractive index of the particle. It always pushes
the particle towards the forward direction irrespective
BehaviorAnalysisofaGaussianBeamOpticalTrapintheRayleighRegime
369

-400 -300 -200 -100 0 100 200 300 400
0
0.2
0.4
0.6
0.8
1
1.2
x 10
-9
Axial distance of particle along z-axis (nm)
Scattering force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 13: Scattering force versus axial distance z of the
particle located at x = 0, y = 0 from the beam center for
different beam waist radii.
-100 -50 0 50 100
0
0.2
0.4
0.6
0.8
1
1.2
x 10
-9
Transverse distance of particle from z-axis (nm)
Scattering force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 14: Axial force versus transverse distance x of the
particle from z-axis at y = 0, z = 14 nm for different beam
waist radii.
of m > 1 or m < 1. Similar to the gradient forces,
0.5 1 1.5 2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
x 10
-8
Refractive index of particle (nm)
Scattering force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 15: Scattering force versus refractive index of the
particle located at x = 0, y = 0, and z = 14nm for different
beam waist radii.
the scattering force also increases with particle size
as seen in Fig. 16. However, the scattering force
always increases with increasing beam waist radius,
which is due to the increased scattering cross-section
σ in Eq. (3). Moreover, the magnitude of axial gra-
dient is around 100 -1000 times larger than that of
10 20 30 40 50 60 70 80 90 100
0
0.2
0.4
0.6
0.8
1
1.2
1.4
x 10
-6
Radius of particle (nm)
Scattering force (arb. unit)
w0=40 nm
w0=60 nm
w0=80 nm
w0=100 nm
Figure 16: Scattering force versus radius of the particle lo-
cated at x = 0, y = 0, and z = 14nm for different beam waist
radii.
the scattering force. The more the beam is focused
(smaller beam waist radius), the more dominant the
axial gradient force becomes with respect to the scat-
tering force, which is necessary to design a stable
three-dimensional trap.
6 CONCLUSIONS
In this paper, a thorough study of the trapping be-
havior of particles in the Rayleigh regime has been
carried out. Force equations for a focused Gaussian
beam have been derived and then numerical simula-
tions were done to study the effects of the position of
the particle in the trap, refractive index of the parti-
cle, particle size, beam waist radius on the trapping
forces. Gradient forces were observed to be greater in
magnitude than the scattering forces.
REFERENCES
Ashkin, A. (1997). Optical trapping and manipulation of
neutral particles using lasers. In Proc. Natl. Acad. Sci.
USA, Vol. 94, pp. 4853–4860. The National Academy
of Sciences of the USA.
Malagino, N., Pesce, G., Sasso, A., and Arimondo, E.
(2002). Measurements of trapping efficiency and stiff-
ness in optical tweezer. In Optics Communications,
Vol. 214, pp. 15–24. Elsevier.
Neuman, K. C. and Block, S. M. (2004). Optical trapping.
In Rev. of Sci. Instrumentations, Vol. 75, no. 9, pp.
2787–2807. American Institute of Physics.
Schaevitz, J. W. (2006). A practical guide to optical trap-
ping. Technical report.
OPTICS2012-InternationalConferenceonOpticalCommunicationSystems
370
