
Tukra: An Abstract Program Slicing Tool
Raju Halder and Agostino Cortesi
DAIS, Universit
`
a Ca’ Foscari Venezia, Venezia, Italy
Keywords:
Program Slicing Tool, Dependence Graph, Abstract Interpretation.
Abstract:
We introduce Tukra, a tool that allows the practical evaluation of abstract program slicing algorithms. The
tool exploits the notions of statement relevancy, semantic data dependences and conditional dependences.
The combination of these three notions allows Tukra to refine traditional syntax-based program dependence
graphs, generating more accurate slices. We provide the architecture of the tool, some snapshots describing
how it works, and some preliminary experimental results giving evidence of the accuracy improvements it
supports.
1 INTRODUCTION
Program slicing emerged a useful technique that ex-
tracts from programs the statements which are rel-
evant to a given behavior. It is a fundamental
operation for addressing many software-engineering
problems, e.g. program understanding, debugging,
maintenance, testing, parallelization, integration, etc.
The original static slicing algorithm by Mark Weiser
(Weiser, 1984) is expressed as a sequence of data-
flow analysis problems and the influence of predi-
cates on statement execution, while Korel and Lasky
(Korel and Laski, 1988) extended it to the dynamic
context and proposed an iterative dynamic slicing al-
gorithm based on dynamic data flow and control in-
fluence. Over the last 3 decades, several works on
program slicing have been proposed based on the de-
pendence graph representation (Agrawal and Horgan,
1990; Horwitz et al., 1990; Sarkar, 1991; Sinha et al.,
1999).
Program slicing can be defined in concrete as well
as in an abstract domain, where in the former case we
consider exact values of the program variables, while
in the latter case we consider some properties instead
of their exact values. The notion of Abstract Program
Slicing was first introduced by Hong, Lee and Sokol-
sky (Seok Hong et al., 2005). Mastroeni and Nicoli
´
c
(Mastroeni and Nikolic, 2010) recently extended the
theoretical framework of slicing proposed by Binkley
(Binkley et al., 2006) to an abstract domain in order
to define abstract slicing, and to represent and com-
pare different forms of slicing in the abstract domain.
Other remarkable works on abstract program slicing
include (Cortesi and Halder, 2010; Mastroeni and Za-
nardini, 2008; Zanardini, 2008; Bhattacharya, 2011).
In (Cortesi and Halder, 2010), the authors ap-
plied the notion of semantic relevancy of statements,
and proposed a slicing refinement for imperative pro-
grams by combining with statement relevancy the no-
tions of semantic data dependences (Mastroeni and
Zanardini, 2008) and conditional dependences (Suku-
maran et al., 2010). The combination of these three
notions allows us to refine traditional syntax-based
dependence graphs into more precise semantics-based
dependence graphs, leading to an abstract program
slicing algorithm that produces more accurate abstract
slices.
In this paper, we introduce Tukra
1
., a tool based
on the theoretical proposal in (Cortesi and Halder,
2010) that allows the practical evaluation of abstract
program slicing algorithms. The tool performs static
intraprocedural slicing of a program in an abstract
domain of interest. We provide the architecture of
the tool, some snapshots describing how it works
and some preliminary experimental results giving ev-
idence of the accuracy improvements it supports. As
far as we know, there is no other similar public tool
available.
The rest of the paper is organized as follows: Sec-
tion 2 presents a short introduction of the existing ab-
stract program slicing algorithm that supports Tukra.
Section 3 describes Tukra’s architecture, some snap-
shots describing how it works and an experimental re-
1
“Tukra” is a hindi word which means “Slice”.
The source code of Tukra can be downloaded from
www.dsi.unive.it/∼avp/Tukra/
178
Halder R. and Cortesi A..
Tukra: An Abstract Program Slicing Tool.
DOI: 10.5220/0004069801780183
In Proceedings of the 7th International Conference on Software Paradigm Trends (ICSOFT-2012), pages 178-183
ISBN: 978-989-8565-19-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

sult on a test program. Section 4 concludes the work.
2 BACKGROUND
The algorithm behind our slicing tool is proposed in
(Cortesi and Halder, 2010) that combines the notions
of statement relevancy, semantic data dependences
and conditional dependences. Let us discuss these
three notions and the slicing algorithm in brief.
In traditional Program Dependence Graphs
(PDGs), the notion of dependences between state-
ments is based on the syntactic presence of a variable
in the definition of another variable or in a condi-
tional expression. Therefore, the definition of slices
at semantic level creates a gap between slicing and
dependences. Mastroeni and Zanardini (Mastroeni
and Zanardini, 2008) first introduced the notion
of semantic data dependences which fills up the
existing gap between syntax and semantics. The
semantic data dependences which are computed
for all expressions in the program over the states
possibly reaching the associated program points,
help in obtaining more precise semantics-based
PDGs by removing some false dependences from the
traditional syntactic PDGs. For instance, although
the expression “e = x
2
+ 4w mod 2 + z” syntactically
depends on w, but semantically there is no depen-
dence as the evaluation of “4w mod 2” is always zero.
This can also be lifted to an abstract setting where
dependences are computed with respect to some
specific properties of interest rather than the concrete
values. For instance, if we consider the abstract
domain SIGN={>, pos, neg, ⊥}, the expression e
does not semantically depend on x w.r.t. SIGN, as
the abstract evaluation of x
2
always yields to pos for
all atomic values of x ∈ {pos, neg}. This is the basis
to design abstract semantics-based slicing algorithms
aimed at identifying the part of the programs which
is relevant with respect to a property (not necessarily
the exact values) of the variables at a given program
point.
Sukumaran et al. (Sukumaran et al., 2010) pre-
sented a refinement of the traditional PDGs into De-
pendence Condition Graphs (DCGs) based on the no-
tion of conditional dependences. A DCG is built from
the PDG by annotating each edge e = e.src → e.tgt
in the PDG with information e
b
= he
R
, e
A
i that cap-
tures the conditions under which the dependence rep-
resented by that edge is manifest. The first compo-
nent e
R
refers to Reach Sequences, whereas the sec-
ond component e
A
refers to Avoid Sequences. The
informal interpretation of e
R
is that the conditions
represented by it should be true for an execution to
ensure that e.tgt is reached from e.src. The Avoid
Sequences e
A
captures the possible conditions under
which the assignment at e.src can get over-written be-
fore it reaches e.tgt. The interpretation of e
A
is that
the conditions represented by it must not hold in an
execution to ensure that the variable being assigned at
e.src is used at e.tgt. It is worthwhile to note that e
A
is relevant only for DDG edges and it is
/
0 for CDG
edges.
Cortesi and Halder (Cortesi and Halder, 2010) ap-
plied the notion of semantic relevancy of statements.
It determines whether an imperative statement is rele-
vant w.r.t. a property of interest, and is computed over
all concrete (or abstract) states possibly reaching the
statement. For instance, consider the following code
fragment: {(1) x = input; (2) x = x+2; (3) print x;}.
If we consider an abstract domain of parity repre-
sented by PAR={>, odd, even, ⊥}, we see that the
variable x at program point 1 may have any parity
from the set {odd, even}, and the execution of the
statement at program point 2 does not change the par-
ity of x at all. Therefore, the statement at 2 is seman-
tically irrelevant w.r.t. PAR. By disregarding all the
nodes that correspond to irrelevant statements w.r.t.
concrete (or abstract) property from a syntax-based
PDG, we obtain a more precise semantics-based (ab-
stract) PDG.
The combined effort of semantic relevancy of
statements with the expression-level semantic data
dependences by Mastroeni and Zanardini (Mastroeni
and Zanardini, 2008) guarantees a more precise
semantics-based (abstract) PDG. A further refinement
of it can be achieved by applying the notion of condi-
tional dependences by Sukumaran et al. (Sukumaran
et al., 2010) that allows us to transform PDGs into
DCGs and to identify unrealizable dependneces in
them under the trace semantics of the programs. The
removal of such unrealizable dependences yields to
more refined semantics-based (abstract) DCGs.
The slicing algorithm GEN-SLICE makes use of
two auxiliary algorithms. Given a program P and an
abstract domain ρ, the algorithm REFINE-PDG gen-
erates semantics-based abstract PDG w.r.t. ρ. The
algorithm REFINE-DCG converts the PDG (which
is refined by the algorithm REFINE-PDG) into a
DCG by computing the annotation over all depen-
dence edges, and then again refines it into more pre-
cise one by removing some unrealizable dependence
paths. Finally, GEN-SLICE performs slicing based
on the dependence graphs obtained this way.
Tukra:AnAbstractProgramSlicingTool
179

3 Tukra
In this section, we identify the possible inputs ex-
pected from the users, and the basic functional mod-
ules required to perform the slicing computations over
the abstract domains.
The aim of designing Tukra is to provide user-
friendly interfaces accelerating users to slice impera-
tive programs in various abstract domains of interest.
When performing abstract slicing of programs, users
must provide the following inputs to Tukra:
1. Program to be Sliced: Tukra is able to perform
slicing of programs covering a subset of impera-
tive language constructs. At this preliminary stage
of implementation, we do not focus on any spe-
cific programming language. We consider the fol-
lowing assumptions on the syntax of the input pro-
grams as below:
• All control blocks should be enclosed with “{}”
irrespective of the number of statements in it.
• Empty control block must have “skip;” state-
ment in it.
• Run-time input for any statement is denoted by
“?”, e.g. “var =?;”.
• The syntax of the statement displaying vari-
ables’ values is “print(x, y, z);” where x, y, z are
the program variables.
Observe that the assumptions above do not cause
severe limitations for Tukra: an improvement of
the tool to support other language constructs can
easily be achieved.
2. Abstract Domain of Interest: We provide two
abstract domains in Tukra at this preliminary
stage of implementation. The first one is SIGN=h
>, pos, neg, zero, ⊥ i that represents the sign
property of variables, and the second one is
PAR=h >, odd, even, ⊥ i that represents the par-
ity property of the variables. However, additional
abstract domains can be integrated by implement-
ing the corresponding interfaces designed for the
abstract domains.
3. Types of Semantic Computations: Tukra can
perform three types of semantic computations:
statement relevancy, semantic data dependences
and conditional dependences in the abstract do-
main chosen before. Users are provided options
to choose either single or combination of multiple
types of semantic computations.
4. Slicing Criterion: A slicing criterion is com-
posed of two components: a program variable v
and a program point p. Observe that in Tukra,
slicing is performed based on the dependence
Program
ExtractInfo
FormMatrix
ComputeSemanticDep
GenTraceSemantics
GenCollectingSemantics
ComputeDCG
annotations
AbstractDomain
Refined Semantics-
based PDG
Syntactic PDG
Figure 1: Tukra’s architecture.
graphs. Therefore, v must be defined or used at
p.
3.1 Tukra’s Architecture
The slicing tool consists of packages for building and
refining dependence graphs, as well as a parser that
translates the input program into an internal represen-
tations convenient for the future computations. We
identify the following key modules for Tukra:
1. ExtractInfo: The module “ExtractInfo” extracts
detail information about the input programs, i.e.
the type of program statements, the controlling
statements, the defined variables, the used vari-
ables, etc for all statements in the program and
store them in a file as an intermediate representa-
tion.
2. FormMatrix: The module “FormMatrix” gen-
erates incidence matrix for Control Flow Graphs
(CFGs) and Program Dependence Graphs (PDGs)
of the input programs based on the information
extracted by the module “ExtractInfo”.
3. GenCollectingSemantics and GenTraceSeman-
tics: Given an abstract domain, these modules
compute the abstract collecting Semantics and ab-
stract trace semantics of the input programs based
on the information extracted by “ExtractInfo” and
the CFG generated by “FormMatrix”.
4. ComputeDCGannotations: This module com-
putes the DCG annotations (Reach Sequences and
Avoid Sequences) for all CDG and DDG edges of
the PDG based on the information extracted by
ICSOFT2012-7thInternationalConferenceonSoftwareParadigmTrends
180

“ExtractInfo” and the PDG generated by “Form-
Matrix”.
5. ComputeSemanticDep: It computes statements
relevancy, semantic data dependences and condi-
tional dependences of the programs under all pos-
sible states reaching each program points of the
program (collecting semantics) and by computing
the satisfiability of DCG annotations under its ab-
stract trace semantics.
The interaction between various modules mentioned
above is depicted in Figure 1. Observe that “FormMa-
trix” generates a syntactic PDG based on which we
can perform syntax-driven slicing w.r.t. a criterion,
whereas “ComputeSemanticDep” refines the syntac-
tic PDG into a semantics-based abstract PDG by com-
puting statement relevancy and semantic data depen-
dences under its abstract collecting semantics, and the
conditional dependences based on the satisfiability of
DCG annotations under its abstract trace semantics.
interface AbstractElement
boolean isOperator();
boolean isValue();
Class AbstractComponent
interface AbstractOperator
String getOperator();
boolean isArithBinaryOperator();
boolean isArithUnaryOperator();
boolean isRelOperator();
boolean isBoolBinaryOperator();
boolean isBoolUnaryOperator();
boolean equals(AbstractOperator op);
void display();
interface AbstractValue
String[] getProperty();
boolean isBottom();
boolean isAtomicValue();
boolean equals(AbstractValue val);
void display();
extends
extends
BoolValue
String val
SignValue
String Val
ParValue
String val
implements
AbstractArithOperator
String op
AbstractBoolOperator
String op
AbstractRelOperator
String op
implements
Figure 2: Designing abstract values and operators.
The design of abstract values, abstract operators,
abstract domains and abstract environments are de-
picted in Figures 2, 3 and 4 respectively. Any ab-
stract value such as sign value, parity value, boolean
value, and any abstract operator such as arithmetic,
relational, boolean operator implement the specifi-
cations represented by the interfaces “AbstractEle-
ment”, “AbstractValue” and “AbstractOperator”. The
abstract domain implements the specifications repre-
interface AbstractDomain
AbstractValue getTop();
AbstractValue getBottom();
AbstractValue getLUB(AbstractValue[] list);
AbstractValue getGLB(AbstractValue[] list);
AbstractValue[] getAtoms(AbstractValue val);
AbstractValue[] getSubValues(AbstractValue val);
AbstractValue evaluate(AbstractArithOperator ArithUnaryOp, AbstractValue val);
AbstractValue evaluate(AbstractArithOperator ArithBinaryOp, AbstractValue val1, AbstractValue val2);
String evaluate(AbstractRelOperator RelOp, AbstractValue val1, AbstractValue val2);
AbstractValue evaluate(AbstractBoolOperator BoolUnaryOp, AbstractValue val);
AbstractValue evaluate(AbstractBoolOperator BoolBinaryOp, AbstractValue val1, AbstractValue val2);
void getAbstractExpressionList(String PostfixExpr, AbstractEnvironment absEnv, LinkedList ExprList);
Figure 3: Interface abstract domain.
class AbstractEnvironment
void setEnvironment(String[] ProgVars, AbstractValue[] val);
void setEnvironment(AbstractValue[] val);
String[] getVariables();
AbstractValue[] getEnvironment();
AbstractEnvironment getModifiedEnvironment(String Variable, AbstractValue newVal);
AbstractValue getVariableValue(String Variable);
AbstractEnvironment getRestrictedEnvironment(String[] ProgVars);
boolean equals(AbstractEnvironment obj);
void display();
AbstractEnvironment getLUB(AbstractEnvironment obj, AbstractDomain ADobj);
boolean isAtomicEnvironment();
LinkedList getAtomicCovering(AbstractDomain ADobj);
LinkedList getXAtomicCovering(String[] X_Vars, AbstractDomain ADobj);
LinkedList getXSubCovering(String[] X_Vars, AbstractDomain ADobj);
String[] vars;
AbstractValue[] env;
Figure 4: Class abstract environment.
sented by the interface “AbstractDomain”. The ab-
stract states at each program point in a program is de-
fined by an abstract environment associated with the
corresponding program point. The abstract environ-
ment is defined by the class “AbstractEnvironment”.
This design allows us to add any new abstract domain
to Tukra by implementing the interfaces correspond-
ing to the new abstract domain.
Tukra is implemented in Java. In Figures 5 and 6,
we show some of the snapshots of the system.
We executed Tukra on a PC running with
2.27GHz Processor, Windows 7 Professional 64-
bit Operating System and 4 GB RAM. Table 1(a)
depicts a test program. Tables 1(b), 1(c) and
1(d) depict syntax-based, semantic data dependence-
based (Mastroeni-Zanadini’s approach) and Cortesi-
Halder’s algorithm-based slicing of the test program
w.r.t. hL11, y, SIGNi.
Tukra:AnAbstractProgramSlicingTool
181
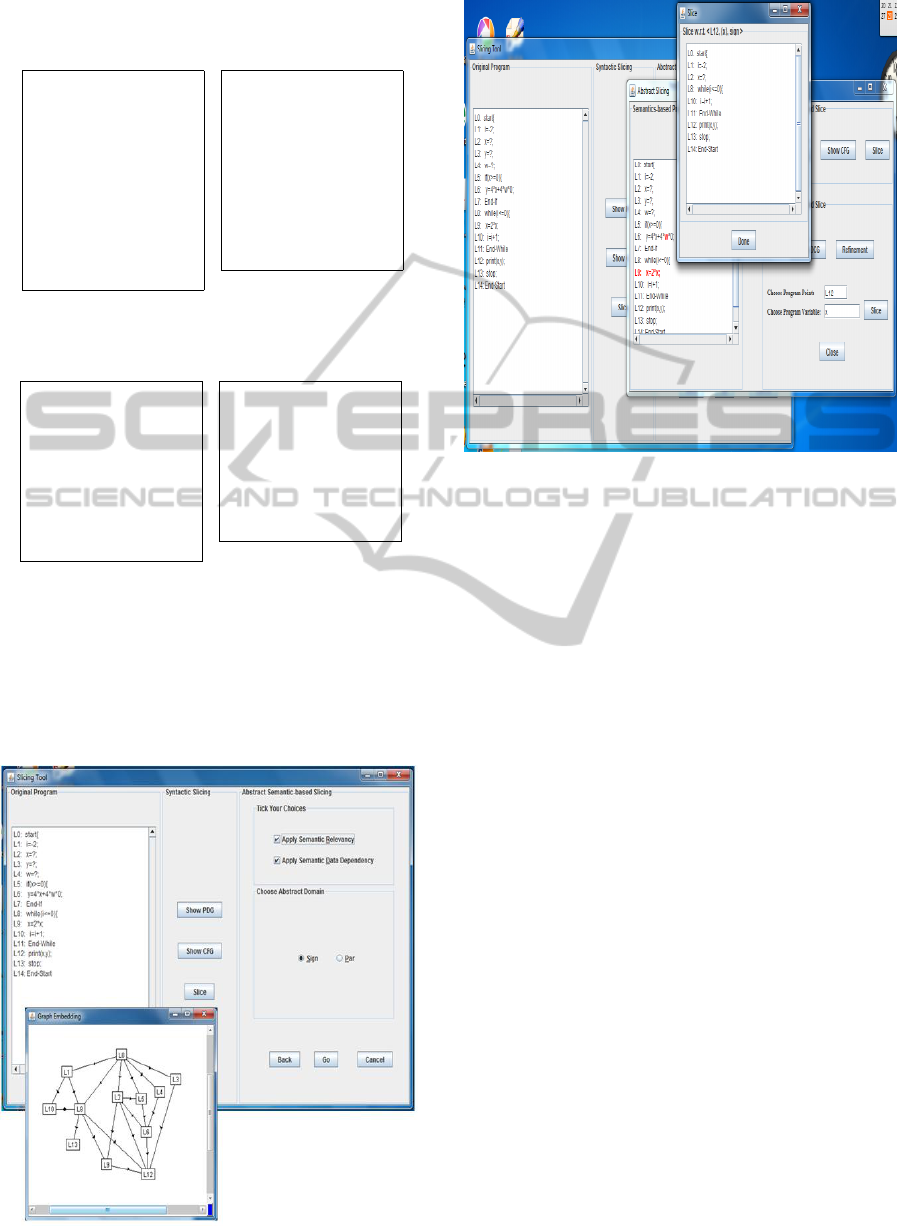
Table 1: A test program and its various slicing.
(a) A test program.
L1 i = −2;
L2 x =?;
L3 y =?;
L4 w =?;
L5 i f (x ≥ 0){
L6 x = x + w;
L7 y = 4 ∗ w ∗ 0; }
L8 while(i ≤ 0){
L9 y = y ∗ 2;
L10 i = i + 1; }
L11 print(x, y);
(b) Syntactic slicing w.r.t.
hL11, yi.
L1 i = −2;
L2 x =?;
L3 y =?;
L4 w =?;
L5 i f (x ≥ 0){
L7 y = 4 ∗ w ∗ 0; }
L8 while(i ≤ 0){
L9 y = y ∗ 2;
L10 i = i + 1; }
L11 print(x, y);
(c) Slicing w.r.t. hL11,
y, SIGNi (Mastroeni-
Zanadini).
L1 i = −2;
L2 x =?;
L3 y =?;
L5 i f (x ≥ 0){
L7 y = 4 ∗ w ∗ 0; }
L8 while(i ≤ 0){
L9 y = y ∗ 2;
L10 i = i + 1; }
L11 print(x, y);
(d) Slicing w.r.t. hL11, y,
SIGNi (Cortesi-Halder).
L1 i = −2;
L2 x =?;
L3 y =?;
L5 i f (x ≥ 0){
L7 y = 4 ∗ w ∗ 0; }
L8 while(i ≤ 0){
L10 i = i + 1; }
L11 print(x, y);
4 CONCLUSIONS
The sound, efficient and effective theoretical support
behind Tukra may make it more attractive to the prac-
Figure 5: Syntactic slicing and PDG generation.
Figure 6: DCG-based slicing.
tical field, as it is able to generate more precise slice
w.r.t. the literature. At present, Tukra can be re-
garded as a first generation system, in that it is mainly
developed to support research. It is now in a prelimi-
nary stage and there are a lot of scopes to improve it
in terms of algorithmic efficiency and generality.
ACKNOWLEDGEMENTS
Work partially supported by RAS L.R. 7/2007 Project
TESLA.
REFERENCES
Agrawal, H. and Horgan, J. R. (1990). Dynamic program
slicing. In Proceedings of the ACM SIGPLAN Confer-
ence on Programming Language Design and Imple-
mentation (PLDI ’90), pages 246–256, White Plains,
New York. ACM Press.
Bhattacharya, S. (2011). Property Driven Program Slic-
ing and Watermarking in the Abstract Interpreta-
tion Framework. PhD thesis, Universit
`
a Ca’ Foscari
Venezia.
Binkley, D., Danicic, S., Gyim
´
othy, T., Harman, M., Kiss,
A., and Korel, B. (2006). A formalisation of the rela-
tionship between forms of program slicing. Science of
Computer Programming, 62(3):228–252.
Cortesi, A. and Halder, R. (2010). Dependence condition
graph for semantics-based abstract program slicing.
In Proceedings of the 10th International Workshop on
ICSOFT2012-7thInternationalConferenceonSoftwareParadigmTrends
182

Language Descriptions Tools and Applications (LDTA
’10), pages 4:1–4:6, Paphos, Cyprus. ACM Press.
Horwitz, S., Reps, T., and Binkley, D. (1990). Inter-
procedural slicing using dependence graphs. ACM
Transactions on Programming Languages and Sys-
tems, 12(1):26–60.
Korel, B. and Laski, J. (1988). Dynamic program slicing.
Information Processing Letters, 29(3):155–163.
Mastroeni, I. and Nikolic, D. (2010). Abstract program
slicing: From theory towards an implementation. In
Proceedings of the 12th International Conference on
Formal Engineering Methods, pages 452–467, China.
Springer LNCS, Volume 6447.
Mastroeni, I. and Zanardini, D. (2008). Data dependencies
and program slicing: from syntax to abstract seman-
tics. In Proceedings of the ACM SIGPLAN symposium
on Partial evaluation and semantics-based program
manipulation, pages 125–134, San Francisco, Califor-
nia, USA. ACM Press.
Sarkar, V. (1991). Automatic partitioning of a program de-
pendence graph into parallel tasks. IBM Journal of
Research and Development, 35(5–6):779–804.
Seok Hong, H., Lee, I., and Sokolsky, O. (2005). Abstract
slicing: A new approach to program slicing based on
abstract interpretation and model checking. In Pro-
ceedings of the 5th International Workshop on Source
Code Analysis and Manipulation, pages 25–34, Hun-
gary. IEEE CS.
Sinha, S., Harrold, M. J., and Rothermel, G. (1999).
System-dependence-graph-based slicing of programs
with arbitrary interprocedural control flow. In Pro-
ceedings of the 21st International Conference on Soft-
ware Engineering (ICSE ’99), pages 432–441, Los
Angeles, CA, USA. ACM Press.
Sukumaran, S., Sreenivas, A., and Metta, R. (2010). The
dependence condition graph: Precise conditions for
dependence between program points. Computer Lan-
guages, Systems & Structures, 36(1):96–121.
Weiser, M. (1984). Program slicing. IEEE Transactions on
Software Engineering, SE-10(4):352–357.
Zanardini, D. (2008). The semantics of abstract program
slicing. In Proceedings of the International Working
Conference on Source Code Analysis and Manipula-
tion, pages 89–100, Beijing, China. IEEE Press.
Tukra:AnAbstractProgramSlicingTool
183
