Autonomous Constructing Everyday Projected Displays

Cui Xie, Qi Wang and Wei Cheng

Department of Computer Science, Ocean University of China, 238 Songling Road, Qingdao, China

Keywords: Projector-based Display, Image Warping, Automatic Geometric Correction, Non-Planar Surface.

Abstract: This paper presents an autonomous geometric correction method to support constructing a projector-based

large display for everyday use, which includes offline and online processing phase. The offline process is

focus on an automatic, fast and robust approach for the geometric registration of projector-camera system.

The online stage is mainly the implementing real-time image warping via modern graphics hardware to

achieve the final corrected images without first acquiring geometric information of the screen’s surface.

Since a simple checkerboard pattern is used to facilitate building the mapping of the corner correspondences

of projector-camera image, and a perspective projection invariant rational Bezier patch is used to

approximately represent the mapping, our method saves a lot of computing time and become easier and

robust. Therefore, the achieved transformation can be used for online image warping for actual projection.

As a result, a layman user can get a corrected image displayed on a non-planar surface for the point of view

of the camera easily.

1 INTRODUCTION

Portable projectors have become increasingly

cheaper, brighter, and smaller. So, projectors have

been widely used as a display tool for many

applications, such as offices, classes, research

institutes and for home entertainment (Jiang, 2007).

Moreover, multi-projector based displays can

provide seamless display with greater view angle,

higher resolution and immersive experience than

other traditional display technologies. So, many

researches are focus on how to create

projector-based large displays automatically and

quickly.

In most projection-based displays, users have to

deal with the geometric distortion of the projected

image when the projector is located far from the

observer and/or when the 3D screen surface is badly

oriented. By camera-based computer vision

techniques, one solution is to do complex geometric

registration including camera/projector calibration

and 3D screen surface recovering to wrap the

projected image for any viewpoint (Sajadi, 2010).

These classes of automatic methods can be achieved

in different ways. Homography based method is

feasible for constructing large display over flat

surfaces (Chen, 2002); (Raij, 2004); (Jiang, 2007);

(Brown, 2002); (Damera-Venkata, 2007). Structured

light patterns are often used for nonplanar

display,which uses a large number of pre-designed

patterns of light to encode the correspondence pixel

position of the camera and the projector, and then

achieve the geometric registration (Tardif, 2003);

(Raskar, 1999); (Aliaga, 2008). However this

method is complex and time-consuming. Raskar et

al. in (Raskar, 2004) use a stereo camera pair to

reconstruct quadric surfaces and propose conformal

mapping and quadric transfer to minimize pixel

stretching of the projected images. The non- linear

optimization of estimation of the parameters of

quadric transfer is too time-consuming. Recent work

of Sajadi et al. (Sajadi, 2011) have shown that it is

possible to register multiple projectors on non-planar

surfaces using a single uncalibrated camera instead

of a calibrated stereo pair when dealing with

vertically extruded surfaces. Both above methods

make its wide application limited to a series of

special non-planar planes.

An easier way is directly to do geometric

registration by establishing correct projector-camera

matches relative to the observer (Tardif,

2003).Unfortunately, due to the non-linear color

distortion of the camera, noise and the complex

illumination conditions, pure color-based matching

strategies between the images of projector and

camera are usually fail. Sun et al. (Sun, 2008)

proposed a robust checkerboard pattern recognition

180

Xie C., Wang Q. and Cheng W..

Autonomous Constructing Everyday Projected Displays.

DOI: 10.5220/0004070701800185

In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems

(SIGMAP-2012), pages 180-185

ISBN: 978-989-8565-25-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

method to help non-planar surface geometry

registration. Sun’s method considers both the

geometric and the color feature of the checkerboard

internal corner, and showed more robustness and

effectiveness than existing corner detection method,

such as Harris, SUSAN, and FAST.

In this paper, we propose an easy way to

automatically build a correct projected display for

everyday users. Our method is motivated by Sun

(Sun, 2008),which use a robust checkerboard pattern

recognition method to build the projector-camera

matches. But different from Sun’s method that using

many planar quad patches to approximate the

nonplanar surface and use homograpy to represent

the mapping between camera and projector

correspondences, our method use rational Bezier

patches to approximately represent the mapping

from camera and projector, which considers the

nonlinearities of projector or camera and achieve

faster and more robust matching.

2 OVERVIEW OF OUR SYSTEM

The proposed system includes one or more

commodity projector for receiving images from the

computer. A common camera is employed to capture

the projected image of projectors and stand for the

position of the viewer. Our method is based on the

following four steps, which can be further divided

into offline and online processing stages. The offline

stage includes the first three steps and the last one is

the real-time stage. More details will be described in

sec. 3.

1). Start projecting and capturing the checkerboard

pattern and detect checkerboard internal crossing

corners.

2). Find camera-projector matchers and build the

transformation R based on the corners

correspondences.

3). Build the similarity transformation S by corners

correspondences and define the spatial

transformation W=R*S for image warp.

4). Using the transformation W=R* S to correct the

geometry of the input image and get the corrected

image for the viewer.

3 DETAIL OF OUR METHOD

3.1 Checkerboard Corner Detection

Considering the distortion of the curved surface,

the quality of the camera and the complex

illumination condition etc., we choose to use the

checkerboard corner detection method of Sun’s

(Sun, 2008) with some implementation changed

and improved. For each pixel P, check it’s

neighbours’ surrounding layer’s points within a

rectangular window(see figure 1). If most of the

surrounding layers with four black and white

intensity shifts, the detected point is a candidate

corner. Then, we refine the corner position with a

cluster method to merge all the detected candidate

corners that are close to each other.

Figure2 (a,b c)

illustrates the detected corners (record as corners

collection N) after clustering with our method.

In order to show the robustness of the corner

detection method, a computer generated source

checkerboard pattern(see figure 3a) is projected on

an arbitrary surface and is captured by a general

low-cost cameras for corner detection test. Do the

above coner detection processing and Opencv’s

(FindChessboardCorner function) (Noah, 2009)

respectively. It is easy to note that our corner

detection result (figure 2(a,b,c)) is better than

Opencv’s result (figure 2(d,e,f)) even with bad

illumination condition and distinct nonplanar surface

deformation.

3 3 3 3 3 3

3 2 2 2 2 2

3 2 1 1 1 2

3 2 1 P 1 2

3 2 1 1 1 2

3 2 2 2 2 2

3 3 3 3 3 3 3

er1

(

)



er2

(

)



er3

(

)



Figure 1: Corner P’s surrounding layers and their four

black and white intensity shifts.

(a) (b) (c)

(d) (e) (f)

Figure 2: Our corners identified result(a,b,c) comparison

with OpenCV’s (d,e,f).

3.2 Corners Matching

In order to recognize the captured checkerboard

pattern, we need to connect the corners into quad

AutonomousConstructingEverydayProjectedDisplays

181

(a) (b) (c)

(d) (e)

Figure 3: A source checkerboard pattern generated by a

computer(a), delaunay triangulation result (b,c) and

regular quad meshes(d,e).

(a) (b)



Figure 4: The recognized corners are connected with lines

in column order in source checkerboard pattern(a) and

projected checkerboard pictures (b,c and d).

meshes and build the corners matching between the

computer generated checkerboard pattern and the

projected checkerboard pictures captured by a

camera. Here we only consider the grids inside the

checkerboard(see figure4a). First, use the delaunary

triangulation method described in the OpenCV

library to connect all the detected corners (see red

lines in figure 3(b,c)). Then we do edge filtering to

remove the redundant or illegal edges and get a

regular quad meshes.

There are two classes of false edges: first is the

edges crossing the background or go through more

than one quad, and the second class is the diagonal

of each quad. For the first class of false edges, we

use a distance threshold to determine a false edge

and remove it. As for the second class of false edges,

we check for the average color around the detected

edges. If the color on both sides of the edge is

similar, it is the redundant edge and should be

removed. Otherwise keep it. Figure 3(d,e) shows the

quad meshes after false edges filtering and a graph

G(N1,E) with a regular grid topology is achieved.

The next step is to map nodes of the grid to the

corners of the pattern.

To do corner matching, from the upper left the

first corner, according to the column coordinates

order, using topological information, the coordinates

labelling can be done easily. Figure 4 gives the

experiment results of the ordered and connected

corners of source checkerboard pattern and projected

checkerboard respectively. Each color represents a

column of corners and the last corner of one column

is connected to the first corner of next column. From

the result ， we can see that the algorithm can

correctly recognize the checkerboard corners on

deformable non-planar surfaces and thus the corners

correspondence is built.

3.3 Constructing Correspondences

Mapping R and R-1

Based on the corner correspondences obtained form

section 3.2, Our method fit a rational Bezier patch

using a non-linear least squares fitting technique to

build the mapping R between these correspondences

from camera image to projector image. The

following experiment results illustrate the

effectiveness of our method. R

-1

means the mapping

from projector image to camera image. To be more

efficient, mappings between each corresponding

point pair can be pre-computed and stored as a pixel

mapping look-up table for online efficient geometric

correction will be more convenient.

3.4 Determining Valid Target Display

Area and Similarity

Transformation S

In order to show the image on a non-planar surface

in an undistorted view with respect to the viewer, a

new proper display area(as is shown in figure 5b)

used for projection of the corrected image, with the

largest possible size, should be defined on the inside

of the captured uncorrected image. Actually, we use

a simple and approximative method to find a

maximum rectangular area within the covered area

of the projector into the camera image. This

rectangle has the same ratio as the initial source

image and has the same center of gravity as the

coverage polygon of the camera image. Then the

expected rectangle can be horizontally and vertically

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications

182

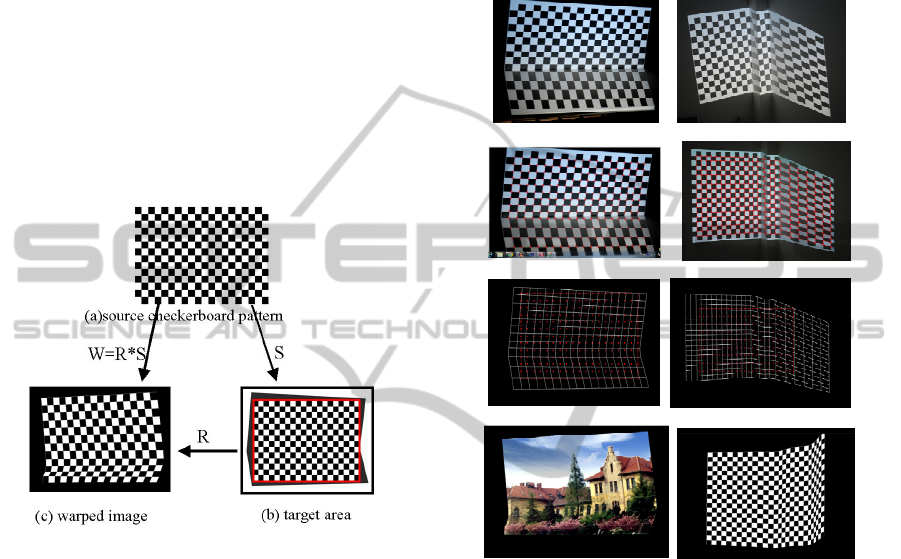
extended starting from the center of the coverage

polygon until one of the corners of the rectangle

reaches the boundary of the coverage polygon. The

red color box of figure 5b shows the valid area used

for actual projection.

Once the target display area is determined, the

correspondences of the corners to the source image

are obtained from a similarity transformation S,

which defines how the source image to be

geometrically corrected in the target area of the

camera image. The similarity transformation S

includes a translation and a scale transformation

between the target display area and the input image.

Figure 6 shows that the original detected corners are

transformed by S into the target rectangle as red

points.

Figure 5: The valid target rectangle area and corners are

transformed into the target rectangle by S.

3.5 Defining Spatial Transformation

The spatial transformation from the source image

(figure 5a) to the target output image(figure 5b)

must be pre-defined to execute

a pre-compensating

inverse distortion(figure 5c) for geometry

correction.



(1) First, do similarity transformation S between the

target rectangle and the source input image to scale

and translate the detected corners into the valid

image area (see figure 5b and figure 6 (b,d)).

(2) Then, apply the transformation R to the corners

of the first processing result and get the warped

transformation W=R*S (figure 5), which maps the

each source corner to the specific target point (see

figure 6 e and f). To be more efficient, mappings

between each corresponding point pair can be stored

as a pixel mapping look-up table for online efficient

geometry correction.

3.6 Online Geometric Correction

Based on hardware-accelerated computer graphics

and combined with an OpenGL texture mapping

technology (see figure 7), the final corrected image

warped by W=R*S can be rendered in real-time and

projected on the screen with visual correct effect.

(a) (b)



(e) (f)

(g) (h)

Figure 6: (a and b) are camera image, (c) is corners

detection result and (d) is quad meshes. (e, f) show the

valid target rectangle area and corners are transformed into

the target rectangle by S. (g and h) are warped image with

texture mapping by transformation R*S.

4 EXPERIMENT

4.1 Geometric Correction with Single

Projector

To test our method, we first use one projector and

one camera to build a simple projector-camera

system. To simplify the experiment, we set the

viewer and the calibration camera to be the same

position and we can ignore the transformation

between camera and viewer.

Firstly, a checkerboard pattern with resolution

1024 * 768 is generated by our computer. Then it is

projected with same resolution on a cylinder screen

AutonomousConstructingEverydayProjectedDisplays

183

(a) camera image (b) 14.2829s



(e) 0.00112791s (f) 0.063615s

(g) 0.776364 s (h) warped image

Figure 7: The computing time spend on each processing

step of our method from (a)the camera captured image to

(h)the warped image: (b)corner detection result, (c)

corners clustering, (d)quad meshes,(e)corners ordering and

checkerboard recognization, (f) valid display rectangle and

similarity transformation, (g) spatial transformation of

corners for geometry correction, and (h) warped image

result.

Figure 8: Two projectors

overlapping.

Figure 9: The valid

rectangle covered area.

and is captured by a camera. Here all the images in

our experiment are pre-processed into size of 1024 *

768 resolution. In figure 7, the computing time used

for each processing step is shown.

Using a computer with an Intel Core 2 Duo 2.13

GHz CPU and a 2GB RAM, our implementation

achieved a recognition speed of 15.52s for a 19*13

checkerboard pattern and 19.26s for a 28*21

checkerboard pattern.

4.2 Geometric Correction with

Multi-projectors

In Figure 8, two projectors are used for

multi-projector setup with necessary projection area

overlapping. Notice that the common region is must

but resulting in unwanted intensity fluctuations. We

can use the intensity blending technique to remove

the bright and provide a seamless correct display. To

ensure good result, each projector should cover an

enough large part of the camera image.

The multi-projector display uses the same

geometric principles as the single projector

projection. As long as the covered area projected by

the projectors is visible to the camera and each

projector need to decide it’s own valid projection

area first (see figure 9). Then, compute the

individual mapping R for each separable area of the

projection by corresponding feature points from the

uncorrected and input images. The similarity

transformation S is obtained and the transformation

R*S is applied to each projector and corrected

images are achieved finally (see figure10).

Figura 10: The final corrected image projection.

5 CONCLUSION AND FUTURE

WORKS

The paper presented a simple auto-geometric

correction method for constructing low-cost smart

projector system, which allows projection on

non-planar surface with an uncalibrated camera by a

layman user. The proposed method solves two cases:

single projector and multiple projectors. The rational

Bezier patch is applied to estimate the mapping

relationship with simple computation. The

experimental results of geometry corrected

projection show that the method is automatic, fast

and accurate. In the future, we will focus on the

universality of the correction algorithm. The

SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications

184

corner-detection time could be decreased using

improved algorithm.

REFERENCES

Jiang Z., Luo X., Mao Y, et al. ,2007. Interactive browsing

of large images on multi-projector display wall

system[C]. Proc. The 12th International Conference

on Human-Computer Interaction. LNCS, vol.

4551,pp. 827-836.

Brown M. S. and Seales W. B., 2002. A Practical and

Flexible Tiled Display System. In Proc of IEEE

Pacific Graphics, pp. 194–203.

Damera-Venkata N., Chang N. L., and DiCarlo Jeffrey M.,

2007.A Unified Paradigm for Scalable Multi-Projector

Displays[J]. IEEE Transactions on Visualization and

Computer Graphics, 13(6), pp.1360-1367.

Tardif J.-P., Roy S., and Trudeau M., 2003.

Multi-projectors for arbitrary surfaces without explicit

calibration nor reconstruction. In Proceeding of

Fourth International Conference on 3-D Digital

Imaging and Modeling, pp.217-224.

Raskar R., Brown M. S., Yang R., Chen W.-C., Welch G.,

Towles H., Seales B., and Fuchs H., 1999.

Multi-projector displays using camera-based

registration. In Proceedings of the 10th IEEE

Visualization 1999 Conference (VIS ’99). Washington,

DC, USA.

Raskar R., J. Baar V., Willwacher T., and Rao S., 2004.

Quadric transfer function for immersive curved screen

displays. Eurographics.

Aliaga D. and Xu Y., 2008. Photogeometric structured

light: A selfcalibrating and multi-viewpoint

framework for accurate 3d modelling. Proc. of IEEE

CVPR.

Sajadi B. and Majumder A., 2010. Auto-calibration of

cylindrical multi-projector systems. In Virtual Reality

Conference (VR), 2010 IEEE, pp. 155 –162 .

Sun W., Yang X., Xiao S., and Hu W., 2008. Robust

checkerboard recognition for efficient nonplanar

geometry registration in Projector-Camera systems. In

Proceedings of the 5th ACM/IEEE International

Workshop on Projector Camera Systems (PROCAMS

'08).

Chen H., Sukthankar R., and Wallace G., 2002. Scalable

Alignment of Large-Format Multi-Projector Displays

Using Camera Homography Trees. In Proceeding of

IEEE Visualization 2002, pages 339–346.

Raij A. and Polleyfeys M., 2004. Auto-calibration of

multi-projector display walls. Proc. of ICPR.

Sajadi B., Majumder A., 2011. Autocalibrating Tiled

Projectors on Piecewise Smooth Vertically Extruded

Surfaces. IEEE Transactions on Visualization and

Computer Graphics, Vol. 17, NO. 9, pp.1209-1221.

Noah K., 2009. OpenCV Tutorial 10 - Chapter 11.

http://dasl.mem.drexel.edu/~noahKuntz/openCVTut10

.html.

AutonomousConstructingEverydayProjectedDisplays

185